轻轨线路曲线半径对车轮磨耗的影响

陈德文 刘飞 左安国 杨新文

摘要： 为分析线路曲线半径对轻轨列车车轮磨耗的影响，以长春市轻轨3号线70%低地板轻轨列车车轮为研究对象，建立独立旋转轮对的轻轨车辆轨道耦合动力学计算模型、轮轨接触模型和Archard材料磨耗模型，对轻轨列车车轮磨耗进行仿真分析。计算结果表明：轻轨列车通过半径为50 m的曲线时，圆曲线上的车轮磨耗比缓和曲线更严重，整体轮对比独立轮对磨耗更严重;曲线半径大于150 m时，内、外侧车轮磨耗随着曲线半径增大而减小，并且在曲线半径相同的条件下，独立轮对各车轮磨耗量均比整体轮对各车轮磨耗量约大2～3 mm;随着列车行驶里程的增加，车轮磨耗率有先增大后减小的变化趋势，即可以将车轮磨耗分为快速磨耗和稳定磨耗2个阶段。轻轨车辆外侧车轮的磨耗率大于内侧车轮，说明车轮磨耗主要发生在外侧车轮。

关鍵词： 轻轨;轮对;曲线半径;耦合动力学;磨耗模型;磨耗率

Abstract： To analyze the influence of curve radius on wheel wear of light rail train， the wheel wear of 70% low floor light rail train of Changchun light rail line 3 is studied， and the vehicletrack coupling dynamic calculation model with independent rotating wheelset， wheelrail contact model and Archard material wear model are established， and then the wheel wear of light rail train is simulated and analyzed. The computing results show that： while the light rail train passes through the 50 m radius curves， the wheel wear on the circular curve is more serious than that on the transition curve， and the wheel wear of the integrated wheelset is more serious than that of the independent wheelset;while the radius of the curve is greater than 150 m， the wear of outside and inside wheel decrease with the radius increasing， and the wear loss  of independent wheelset is about 2～3 mm larger than that of integral wheelset when the curve radius is same;with the train mileage increasing， the wheel wear rate increases first and then decreases， that is， the wheel wear can be divided into fast wear stage and stable wear stage. The wear rate of the outside wheel is higher than that of the inside wheel， which indicates that the wheel wear mainly occurs in the outside wheel.

Key words： light rail;wheelset;curve radius;coupling dynamics;wear model;wear rate

0 引 言

轻轨车辆运行普遍存在轮缘异常磨耗使

游间变大，导致车辆在直线段运行过程中横向摆动幅度较大，严重影响乘客乘坐的舒适度和列车运行安全。长春轻轨3号线位于城市核心区边缘，呈U形，存在众多小半径曲线轨道 [1]，因此选择该线路对轻轨列车车轮磨耗进行研究。

国内外关于车轮磨耗问题已开展一系列的试验、仿真和线路测试工作。JENDEL[2]基于Archard磨耗模型结合试验数据建立车轮踏面磨耗模型。丁军君等[3]基于Archard材料磨耗模型和轮轨多点非椭圆接触理论，模拟低地板有轨电车车轮磨耗演变过程，研究不同轮对内侧距的车轮磨耗问题。李霞[4]和LI等[5]

建立车轮磨耗理论计算模型，采用改进的三维非Hertz滚动接触模型，结合车轮每次通过接触斑内网格时轮轨接触状态的改变，可以更精确地计算车轮滚动时接触斑内的情况，并对目前采用较多的车轮型面磨耗的平滑方法进行总结，指出传统的五点三次平滑、三次样条平滑的缺点，首次提出超光平滑的概念和方法。周业明等[6]参考相关标准，以Ri60R2槽型轨为例，从车轮导向尺寸匹配、车轮强度和踏面镟修经济性等方面讨论有轨电车车轮轮缘的最大磨耗限度，并给出车轮轮缘磨耗的最大推荐值。李涛等[7]以深圳地铁9号线列车车轮轮缘严重磨耗问题为例，结合实测数据，分析车轮镟修后行驶里程与踏面磨耗、轮缘磨耗的关系，分析列车运行的平稳性，并提出相应的改进措施。于春广等[8]结合现场试验，分析某地铁线路的磨耗特征，阐述造成轮缘偏磨的原因，从轮轨关系的角度探究一系纵向刚度和摩擦系数等对车轮磨耗的影响，提出相应的车轮磨耗减缓措施。司道林等[9]和都敏等[10]研究我国重载铁路和城市轨道交通钢轨轨底坡设置对钢轨磨耗的影响。

为探究轻轨列车通过曲线时不同曲线半径对车轮磨耗的影响，建立轻轨车辆车轮磨耗预测分析模型，包括独立旋转轮对的轻轨车辆轨道耦合动力学计算模型、轮轨接触模型和Archard材料磨损模型。基于这些模型计算分析曲线半径对轻轨列车车轮磨耗的影响。

1 车轮磨耗预测模型

1.1 模型计算流程和模型建立

车轮磨耗预测模型的计算流程见图1。首先，利用轻轨车辆轨道耦合动力学模型求解轮轨接触点需要的动力学参数;然后，采用Hertz接触算法求解法向接触应力，利用FASTSim数值方法求解切向接触应力;最后，基于Archard材料磨耗模型计算车轮磨耗。设定车轮磨耗量达到0.10 mm后更新车轮踏面，并进入下一次迭代。

采用多体动力学软件，对采用独立旋转轮对的低地板轻轨列车进行建模，见图2。

全车由“动车+拖车+动车”形式的3个模块组成，其中动车轮对为传统整体轮对、拖车轮对为独立旋转轮对。

车轮模型采用LM型标准车轮，钢轨采用R50标准钢轨，轨道不平顺采用现场实测的不平顺。

车辆轨道系统是一个复杂的多刚体、多自由度、非线性振动系统，不仅车辆各组件内部存在复杂的相对运动和相互作用力，而且

车辆和轨道也存在复杂的轮轨关系，因此在建模时需要对轨道和车辆进行一定的简化或者假设。轻轨车辆轨道耦合动力学计算模型的主要假设为：（1）将轴桥轮组、转向架构架、车体等部件视作刚体，忽略其弹性变形;（2）车体、转向架、轴桥轮组等结构完全对称。低地板列车动力学模型主要参数见表1。

1.2 模型验证

采用文献[3]的经典算例，通过计算结果对比验证本文车轮磨耗模型的正确性。曲线线路参数设置为曲线半径100 m、通过速度36 km/h、曲线平衡超高90 mm。将车轮磨耗量达到0.10 mm作为踏面更新条件，经过30次迭代，得到独立旋转轮对的磨耗量，与文献[3]的研究结果对比见图3和4（x为车轮踏面横向坐标，正数方向为轮缘侧）。

本文模型与文献[3]计算的轮轨磨耗位置和变化规律总体相似，磨耗量相差不大，因此验证本文模型可用于轻轨车轮磨耗预测和后续磨耗影响因素分析。

2 结果分析

2.1 轻轨车辆通过曲线轨道时车轮磨耗分析

计算选取的曲线线路示意见图5，其中：横向坐标表示沿线路长度里程;ZH、HY、QZ、YH、HZ分别表示直缓点、缓圆点、曲中点、圆缓点和缓直点。设定列车通过曲线的速度v、曲线轨道半径R和曲线超高h，列车在线路上循环运行，累计行驶1 000 km后第1节动车和拖车轮对的车轮磨耗量见图6（x为车轮踏面横向坐标，正数方向为轮缘侧）。

由图6可知，在半径为50 m的曲线线路上，列车累计行驶1 000 km后，与前、后缓和曲线相比，圆曲线上的车轮磨耗更严重。进一步分析轮对的磨耗量发现，整体轮对比独立轮对磨耗量更大，即整體轮对磨耗更为严重。

2.2 曲线半径对轻轨列车车轮磨耗的影响

为研究车辆通过曲线时曲线半径对车轮磨耗量的影响，仿真分析分别采用半径为150、250、350、450、550和1 000 m的不同曲线，列车行驶速度取30 km/h，曲线的缓和曲线长度、圆曲线长度、平衡超高、轨距加宽等标准参数见表2。

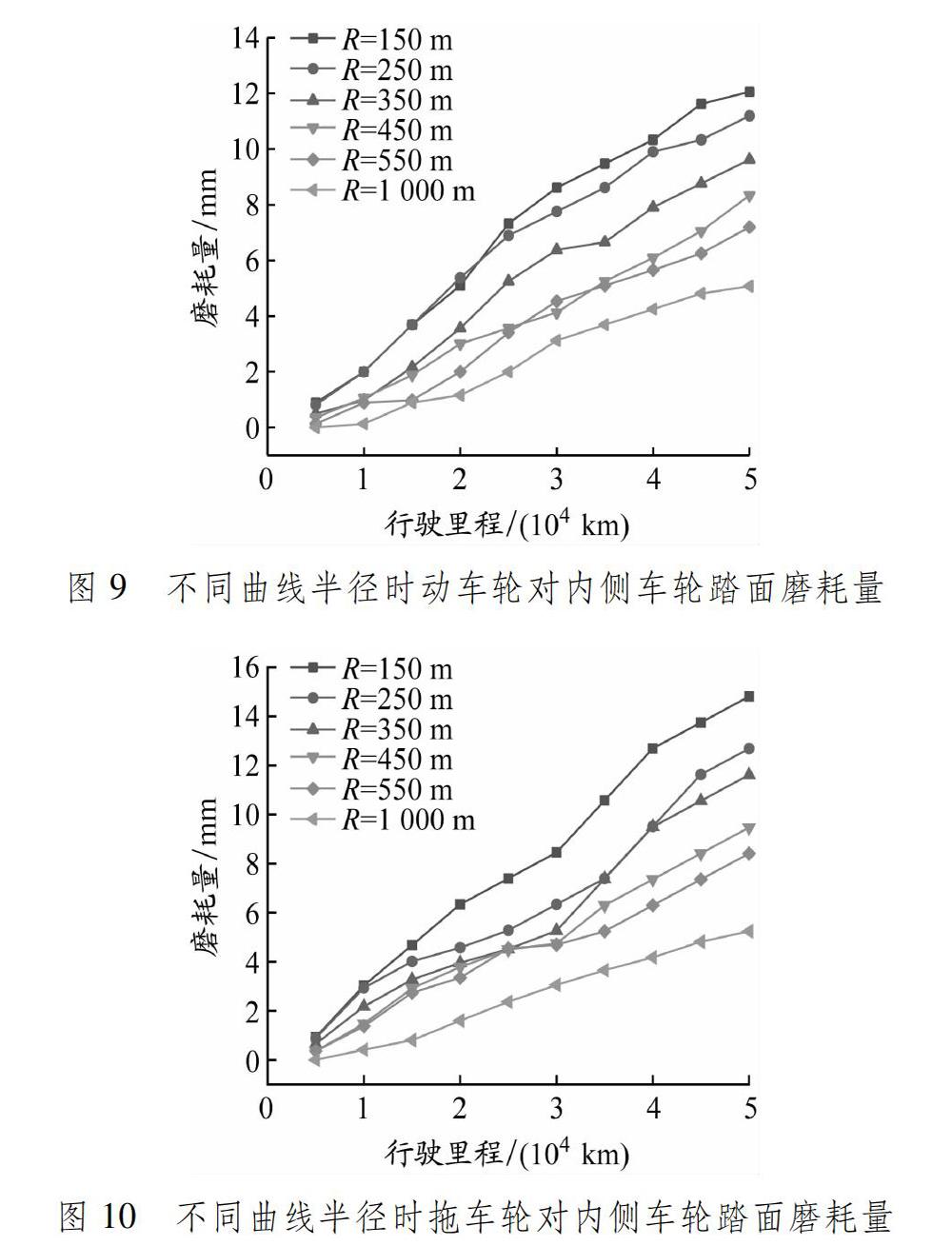
主要分析车轮轮缘偏磨最大值和踏面磨耗最大值。列车在不同曲线半径线路上运行，动车轮对和拖车轮对车轮的磨耗量折线图分别见图7～10。

由图7和8可知，随着列车行驶里程的增加，外侧车轮轮缘偏磨量基本呈线性增长。动车轮对外侧车轮轮缘偏磨量最大值发生在曲线半径为150 m的工况，其值为16.67 mm;随着曲线半径增加，列车行驶里程达5×104 km时，轮缘偏磨量最大值逐渐稳定，说明曲线半径越小对外侧车轮轮缘偏磨越不利，轮缘磨薄、游间变大、晃车加剧，进而行车安全受到威胁。拖车轮对外侧车轮轮缘偏磨量最大值同样发生在曲线半径为150 m的工况，其值为19.46 mm;轮缘偏磨量最大值随半径变化规律与动车轮对相同，但在相同小半径曲线工况下，独立轮对外侧车轮的轮缘偏磨量比整体轮对外侧车轮的轮缘偏磨量约大2～3 mm，独立轮对的轮缘偏磨问题更严重。当曲线半径增大至550 m甚至1 000 m时，动车轮对和拖车轮对外侧车轮轮缘偏磨量都显著减小，说明增大曲线半径能有效减小车轮轮缘偏磨。随着列车行驶里程增加，外侧车轮轮缘偏磨量增加速度较快，当列车行驶里程增加至2×104 km左右时，磨耗量增长速率开始下降，磨耗量的增长变得缓慢，说明此时轮轨型面匹配较好，轮轨接触达到较为理想的状态。

由图9和10可知，随着列车行驶里程增加，轮对内侧车轮踏面磨耗量基本呈线性增长。动车轮对内侧车轮踏面磨耗量最大值发生在曲线半径为150 m的工况，其值为12.05 mm;随着曲线半径的增加，列车行驶里程达5×104 km时，轮缘偏磨量最大值逐渐稳定，说明半径越小对内侧车轮踏面磨耗越不利，进而造成踏面塌陷，加剧磨耗。拖车轮对内侧车轮踏面磨耗量最大值同样发生在曲线半径为150 m的工况，其值为14.80 mm;最大值随半径变化规律与动车轮对相同，但在曲线半径相同的工况下，独立轮对内侧车轮踏面磨耗量比整体轮对内侧车轮踏面磨耗量约大2～3 mm，独立轮对的踏面磨耗问题更严重。当曲线半径增大至550 m甚至1 000 m时，动车轮对和拖车轮对内侧车轮踏面磨耗量增长速度均显著减小，动车轮对和拖车轮对车轮踏面磨耗量相近，说明当曲线半径较大时整体轮对和独立轮对的车轮踏面磨耗量相近。随着行驶里程的增加，内侧车轮踏面磨耗量增长速度较快，当行驶里程增加至3×104 km左右时，磨耗增长速率开始下降，磨耗量的增长变得缓慢，说明此时轮轨型面匹配较好，轮轨接触达到较为理想的状态。

为研究曲线半径对车轮磨耗的影响，定义车轮磨耗率为列车通过单位长度曲线轨道的车轮磨耗面积。

取动车和拖车磨耗率的平均值，曲线半径对轮对内、外侧车轮磨耗率的影响分别见图11和12。

由图11和12可知，随着列车行驶里程的增加，车轮磨耗率有先增大后减小的变化趋势，即可以将车轮磨耗分为快速磨耗和稳定磨耗2个阶段：在新车轮投入运行阶段（行驶里程0～1.5×104 km），轮轨未形成较好的匹配，车轮踏面与钢轨型面处于彼此磨合阶段，车轮磨耗较快;在列车运行中后期阶段（行驶里程大于3.5×104 km），车轮踏面经过前期的磨合，与钢轨型面已基本形成良好的配合，车轮磨耗率逐渐减小，虽然随着行驶里程的增加车轮踏面磨耗率有小幅变动，但仍处于稳定磨耗阶段。当曲线半径由550 m增大到1 000 m时，车轮磨耗率虽然有所减小，但趋势不明显，说明对于轻轨车辆，大半径曲线的曲线半径变化对磨耗率的影响较小。通过对比轮对内、外侧车轮磨耗率可以发现，外侧车轮的磨耗率大于内侧车轮。从磨耗量计算结果可以看出，外侧车轮的轮缘偏磨量和踏面磨耗量更大，故其磨耗率较大，说明列车通过曲线时，车轮磨耗集中发生在外侧车轮，应及时对外侧车轮进行镟修或更换。

3 结 论

基于建立的轻轨车辆车轮磨耗预测分析模型，计算并分析曲线半径对轻轨列车车轮磨耗的影响，得到以下结论：

（1）轻轨列车通过半径为50 m的曲线时，与前、后缓和曲线相比，圆曲线上的车轮磨耗更严重，整体轮对比独立轮对车轮磨耗更严重。

（2）随着列车行驶里程的增加，外侧车轮轮缘偏磨量和内侧车轮踏面磨耗量基本呈线性增长。曲线半径大于150 m时：曲线半径越小外侧车轮轮缘偏磨越大，会造成轮缘磨薄、游间变大，加剧晃车现象，从而威胁行车安全;曲线半径越小内侧车轮踏面磨耗越大，会造成踏面塌陷，加剧磨耗;当曲线半径较大时，曲线半径变化对整体轮对和独立轮对的踏面磨耗影响一致。在列车通过相同条件的小半径曲线时，独立轮对外侧车轮轮缘偏磨量和内侧车轮踏面磨耗量均比整体轮对约大2～3 mm。

（3）随着曲线半径的增大，同一行驶里程下车轮的磨耗率有所下降，曲线半径的增大有利于减轻车轮磨耗，提高列车运行稳定性和安全性。当曲线半径大于550 m时，随着曲线半径的增大，磨耗率虽然有所减小，但趋势不明显。

（4）随着列车行驶里程的增加，车轮磨耗率有先增大后减小的变化趋势，即可以将车轮磨耗分为快速磨耗和稳定磨耗2个阶段。轻轨车辆外侧车轮的磨耗率大于内侧车轮，车轮磨耗集中发生在外侧车轮，应重点关注外侧车轮磨耗。

参考文献：

[1] 王超生. 长春市轻轨规划的优化调整与设计[J]. 现代城市轨道交通， 2004（4）： 58. DOI： 10.3969/j.issn.16727533.2004.04.002.

[2] JENDEL T. Prediction of wheel profile wear： Comparisons with field measurements[J]. Wear， 2002， 253（1）： 8999. DOI： 10.1016/S00431648（02）00087X.

[3] 丁軍君， 杨阳， 李芾， 等. 基于槽型轨的低地板有轨电车车轮磨耗及优化研究[J]. 铁道学报， 2017， 39（7）： 5459. DOI： 10.3969/j.issn.10018360.2017.07.008.

[4] 李霞. 车轮磨耗预测初步研究[D]. 成都： 西南交通大学， 2009. DOI： 10.7666/d.y1573579.

[5] LI X， YANG T， ZHANG J， et al. Rail wear on curve of a heavy haul line： Numerical simulations and comparison with field measurements[J]. Wear， 2016（366/367）： 131138. DOI： 10.1016/j.wear.2016.06.024.

[6] 周业明， 刘玉文. 有轨电车车轮轮缘磨耗最大限度的探讨[J]. 城市轨道交通研究， 2017， 20（6）： 2124. DOI： 10.16037/j.1007869x.2017.06.006.

[7] 李涛， 刘志远， 赵卓， 等. 城市轨道交通车辆车轮轮缘严重磨耗分析[J]. 城市轨道交通研究， 2018， 21（11）： 7477. DOI： 10.16037/j.1007869x.2018.11.016.

[8] 于春广， 陶功权. 地铁车轮磨耗测试及数值仿真[J]. 工程力学， 2016， 33（1）： 201208. DOI： 10.6052/j.issn.10004750.2014.06.0484.

[9] 司道林， 王继军， 孟宏. 钢轨轨底坡对重载铁路轮轨关系影响的研究[J]. 铁道建筑， 2010（5）： 108110. DOI： 10.3969/j.issn.10031995.2010.05.034.

[10] 都敏， 张军， 王春艳， 等. 城市轨道交通线路轨底坡对钢轨磨耗的影响[J]. 铁道机车与动车， 2014（6）： 15. DOI： 10.3969/j.issn.10031820.2014.06.001.

（编辑 武晓英）