一种低功耗自诊断双阈值超声波传播时间检测法

毛 凯，胡 亮，付 新

(浙江大学，流体动力与机电系统国家重点实验室，浙江杭州 310027)

0 引言

超声波流量计作为一种新型的流量计，与传统的涡街流量计、罗茨流量计、涡轮流量计相比，具有量程比宽、压力损失小，测量精度高、无可动部件、维护成本低等优点，近来被广泛应用于天然气行业，用于检测管道天然气的流量，实现准确公平的贸易计量[1-3]。

超声波流量计根据不同的测量原理可分为相关法、波束偏移法、多普勒法、噪声法和时差法[4-5]。由于时差法在保证较高测量精度的前提下，具有功耗低、灵敏度高、算法简单、数据处理量小、无需对测量介质添加任何颗粒物等优点，因此被广泛应用于超声波流量计中。时差法通过检测超声波信号顺流传播时间值与逆流传播时间值，获取其时间差来计算被测介质的流速或流量，因此准确检测超声波信号的顺、逆流传播时间值是时差法超声波流量计的关键[6-8]。

在时差法超声波流量计中，通常使用阈值法来检测超声波信号在被测介质中的传播时间值。当超声波信号幅值发生变化时，容易使阈值触发在超声波信号的不同上升沿，而非始终是触发在同一个上升沿，导致测量得到的超声波信号传播时间值相差约为其信号周期的整数倍，此现象称之为跳波[9]。因此，在实际使用中，要准确获取超声波信号的传播时间值，关键在于解决由于温度变化、压力变化以及介质变化引起的跳波问题。通常有两种思路来解决或者抑制跳波问题，一种思路是通过超声波信号的整体特征来准确判断超声波信号的起振点，如L.Angrisani[10-11]、Z. J. Yao[12]等，提出用离散卡尔曼滤波算法、无迹卡尔曼滤波算法、多平方根无迹卡尔曼滤波算法来降低超声波信号起始点波形扭曲带来的影响，以提高超声波信号起始点的识别精度；为了进一步提高超声波接收信号起始点的检测精度和缩短计算时间，F. Zhou[13]、H. Hou[14]、Z. Fang[15]等提出了蚁群算法、遗传蚁群优化算法和人工鱼群-粒子群优化算法。上述识别超声波信号起始点的方法，都采用了非常复杂的算法，对硬件设计和软件设计都有较高的要求，功耗较大。所以，另一种思路是通过超声波信号的局部幅值或者相位特征来解决或者抑制跳波问题，如汪伟[16]等基于阈值比例系数基本不变的前提，提出了可调阈值法，Y. Huang[17]等提出相位调制法，张兴红[18]等提出了最大幅值识别法，Z. H. Fang[9]，陈洁[19]等提出了双阈值法，但上述方法均属于实验统计法，要求样本量较大。

因此，为了在低功耗前提下提升超声波流量计的测量上限，测量可靠性、信息化水平、智能化水平等，提出了一种低功耗自诊断双阈值超声波传播时间检测法。与传统单阈值检测方法比较，不仅保留了低功耗的特点，而且能够实现跳波方向的判断和数量的统计，从而进行自我诊断，优化信号，提高测量可靠性，提升测量上限，拓宽量程比。另外还能够提供产品性能变化趋势，实时预警，监控介质特性的变化和产品性能的变化，使得产品的售后服务、维修等更快捷方便。

1 方法

1.1 传统阈值法的跳波问题

如图1所示，时差法超声波流量计是通过安装在测量管上、下游的换能器T1和T2，发射和接收超声波信号来获取其在介质中的传播时间，然后根据上述传播时间差值来计算介质的流速或者流量。

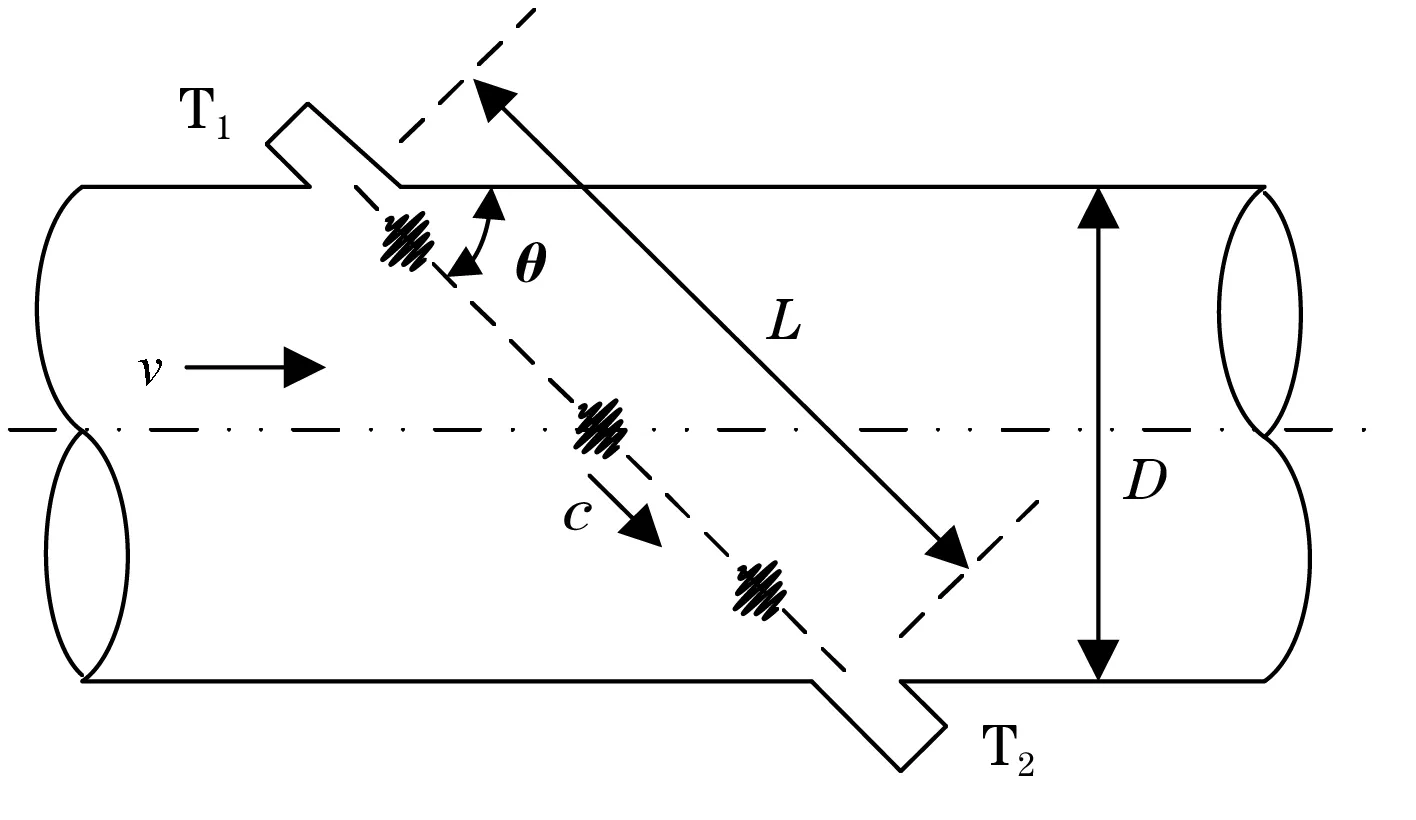
图1 时差法测量原理

图1中D为被测管道的内径，L为超声波信号传播距离，θ为换能器的安装夹角，v为被测介质的平均流速，c为超声波在被测介质中的传播速度。超声波信号顺流传播时间表征值t顺流与逆流传播时间表征值t逆流以及被测介质的平均流速可分别由式(1)、式(2)和式(3)计算得到[6-8]。

(1)

(2)

(3)

根据图1所示的测量原理，时差法超声波流量计能够实现可靠测量的关键是可靠获取超声波信号在被测介质中的传播时间。在实际应用中，为了方便室外安装维护，通常需采用内置电池供电，因此普遍采用单阈值比较法来获取上述传播时间。如图2所示，当超声波信号幅值第一次越过阈值时，使能计时芯片，然后通过捕获随后的过零点Z1、Z2、Z3来作为超声波信号在被测介质中的传播时间。由于硬件和数据处理带来的固定延迟相比于超声波信号在被测介质中的传播时间比较小，又在式(3)的分子项中可以消除，只对分母有略微影响，所以可采用t顺流和t逆流来近似计算流速v。

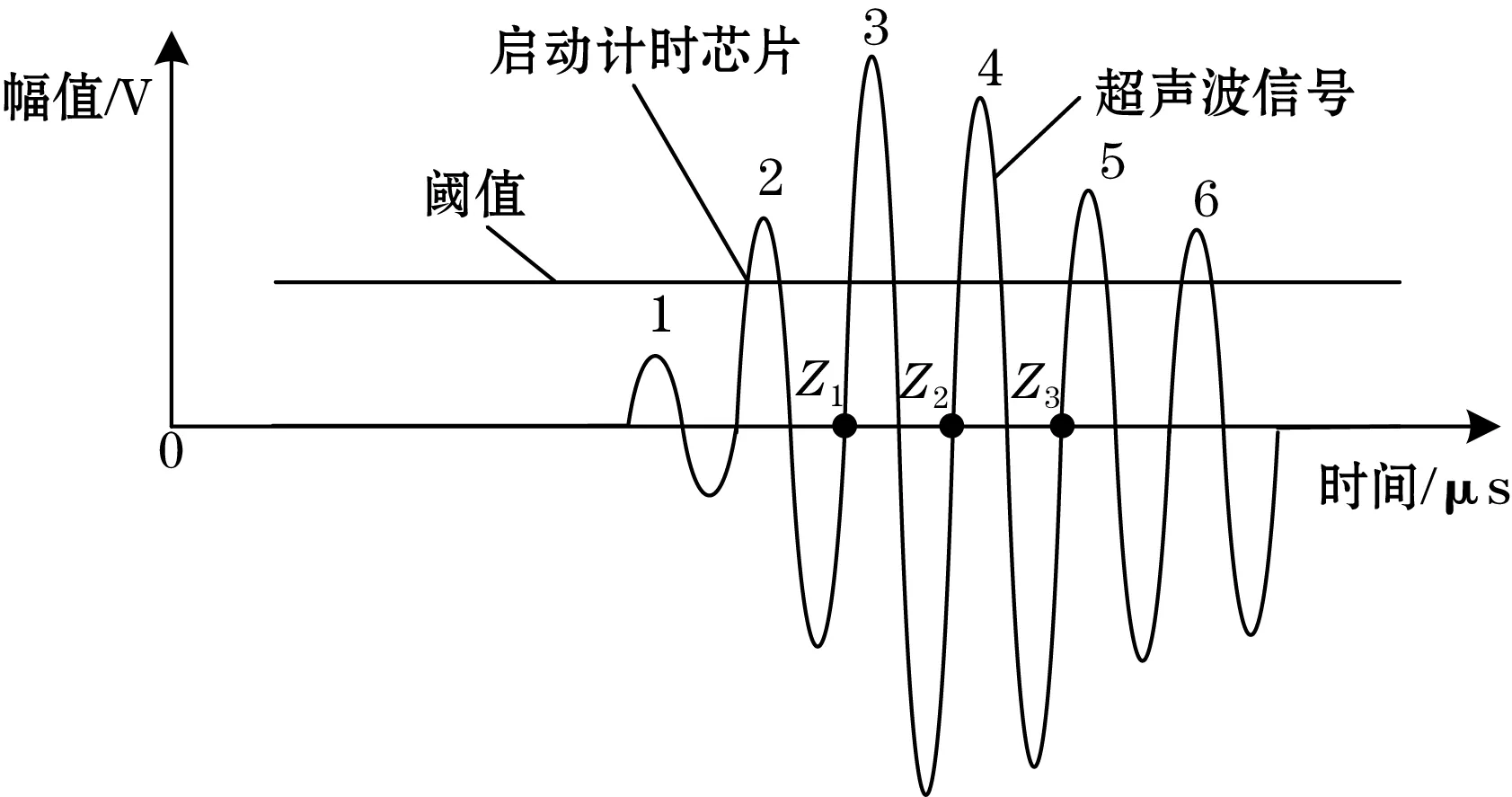
图2 单阈值法测量原理

单阈值法方法简单，功耗低，但显然容易受到超声波信号幅值变化的影响。当超声波信号因温度、压力或者介质变化导致幅值发生如图3所示的变化时，使能计时芯片的触发点由原来的D2变成D3，向后跳跃了一个周期，就发生跳波现象。

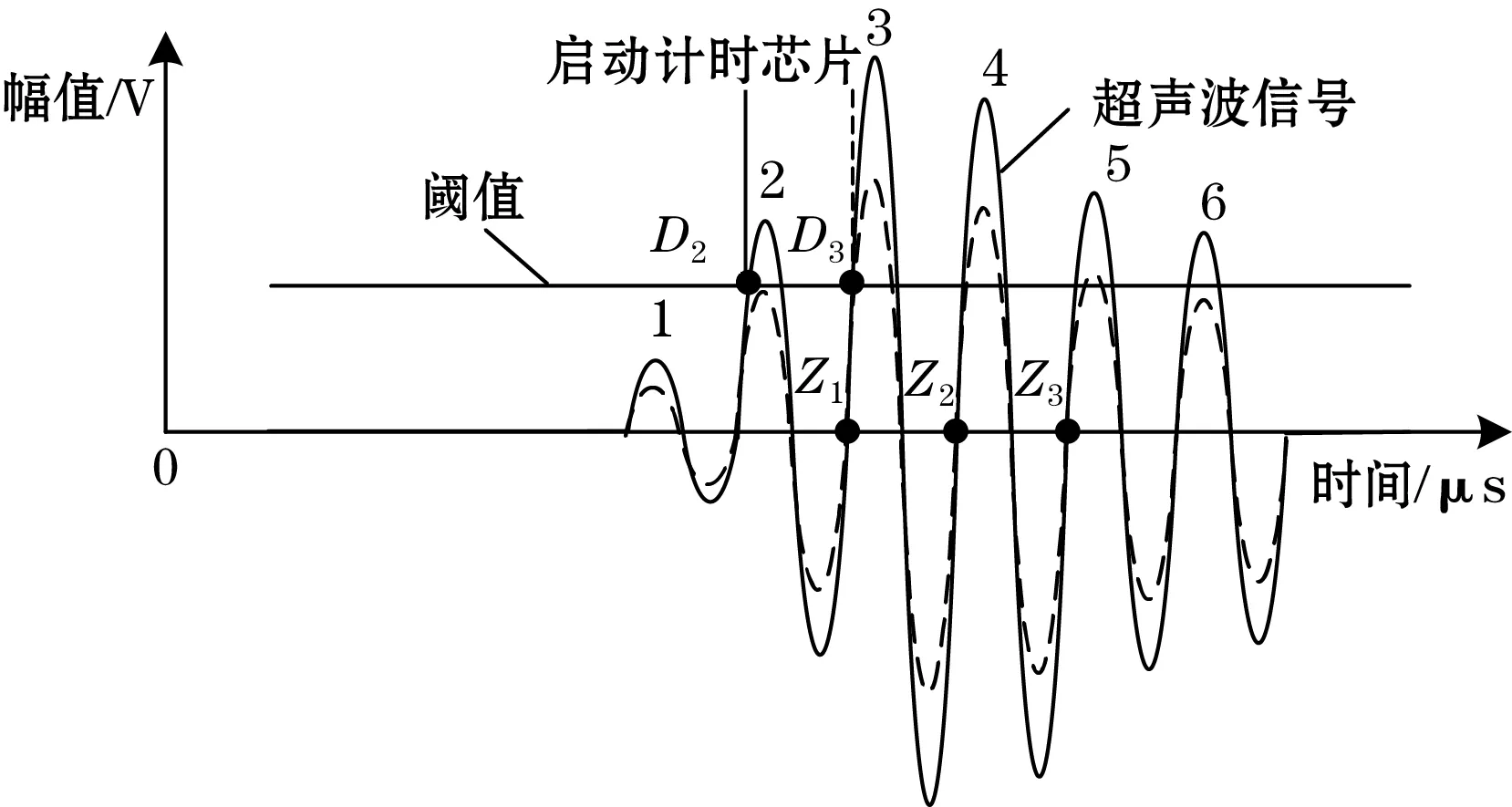
图3 超声波信号幅值变化导致跳波

通常，为了解决上述跳波问题，采用可调阈值法[16]。可调阈值法通过对超声波信号的采样，实现对幅值的实时跟踪，并根据其最大幅值来调整阈值大小，以抑制跳波现象的产生。显然，可调阈值法的关键参数是阈值比例系数TFS，其值可以由式(4)近似获得：

(4)

式中：TFSi+1为触发在超声波信号第i个波上升沿的阈值比例系数；Vi为超声波信号第i个波峰的幅值；i正整数；Vmax为超声波信号的最大幅值。

由于TFS的获取通常基于实验统计，所以样本量的大小，实验环境差异，都会对实际使用产生一定的影响，而且一旦发生跳波，流量计本身不能自动诊断，进行修正，测量结果将具有很大的不确定。

1.2 低功耗自诊断双阈值法

低功耗自诊断双阈值法在上述可调单阈值法的基础之上仅需引入一个如图4所示的第二阈值(第二阈值小于第一阈值)，即可在低功耗模式下实现跳波自诊断，进而有效抑制跳波的产生。

低功耗自诊断双阈值法主要分为3个部分：

第1部分，如图4所示，主要作用是产生3个连续的诊断窗口W1、诊断窗口W2和诊断窗口W3。超声波信号幅值首次越过第一阈值后，经阈值单次触发保持产生信号a，经第二阈值反复触发产生带计时脉冲串的信号b，信号a与信号b进行逻辑与之后产生信号c，信号c经过逻辑非操作之后产生信号d，信号d经过下降沿触发保持后产生信号e，信号e经单稳态触发器后产生带诊断窗口W1的信号f，同时信号e与信号f进行逻辑异或之后产生信号g，信号g经过单稳态触发器后产生带诊断窗口W2的信号h，同时信号g与信号h进行逻辑异或之后产生信号i，信号i经过单稳态触发器后产生带诊断窗口W3的信号j。所以，3个诊断窗口的开启时间(上升沿)由信号c的第一个脉冲上升沿决定。

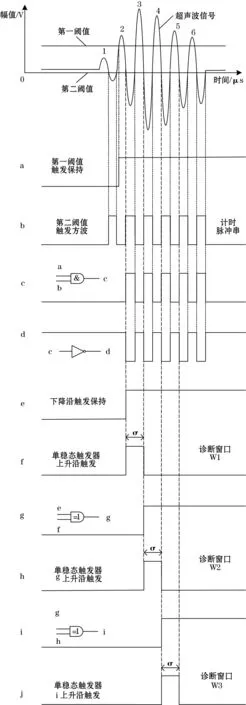
图4 计时脉冲串和诊断窗口产生原理

第2部分，如图5所示，主要作用是产生计时用的计时脉冲。超声波信号经第二阈值反复触发产生信号b，信号b经过一定的延时τ1产生信号b1，信号b与信号b1经过逻辑与产生信号b2，信号b2经过单稳态触发器后产生信号b3，信号b3经过一定的延时τ2产生信号b4，信号b3与信号b4经过逻辑与产生信号b5，信号b5经过逻辑非操作之后产生信号b6，信号b6经过下降沿触发保持后产生信号b7，信号b7经过单稳态触发器后产生信号b8，信号b8经过一定的延时τ3产生带计时脉冲TP的信号b9。所以，计时脉冲TP的上升沿由计时脉冲串第3个脉冲的上升沿决定。

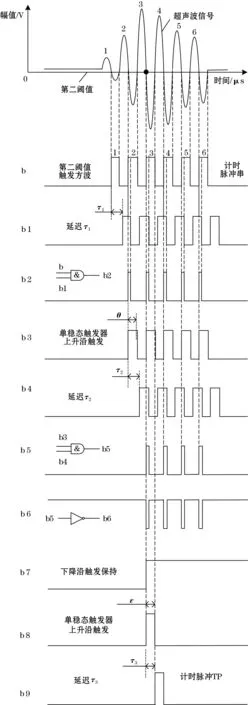
图5 计时脉冲产生原理

τ1、τ2、τ3、θ和σ需满足式(5)的要求：

(5)

式中T为超声波信号周期。

第3部分，如图6所示，主要作用是根据计时脉冲分别落在各诊断窗口中的情况来诊断跳波情况。跳波可分为3种情况，往前跳波、无跳波和往后跳波。图6中，b(F1)为往前跳一个波，b(N)为无跳波，b(B1)为往后跳一个波，这3种情况在实际使用中较为常见。其中，Fm代表往前跳波数，m为正整数；Bn代表往后跳波数，n为正整数。

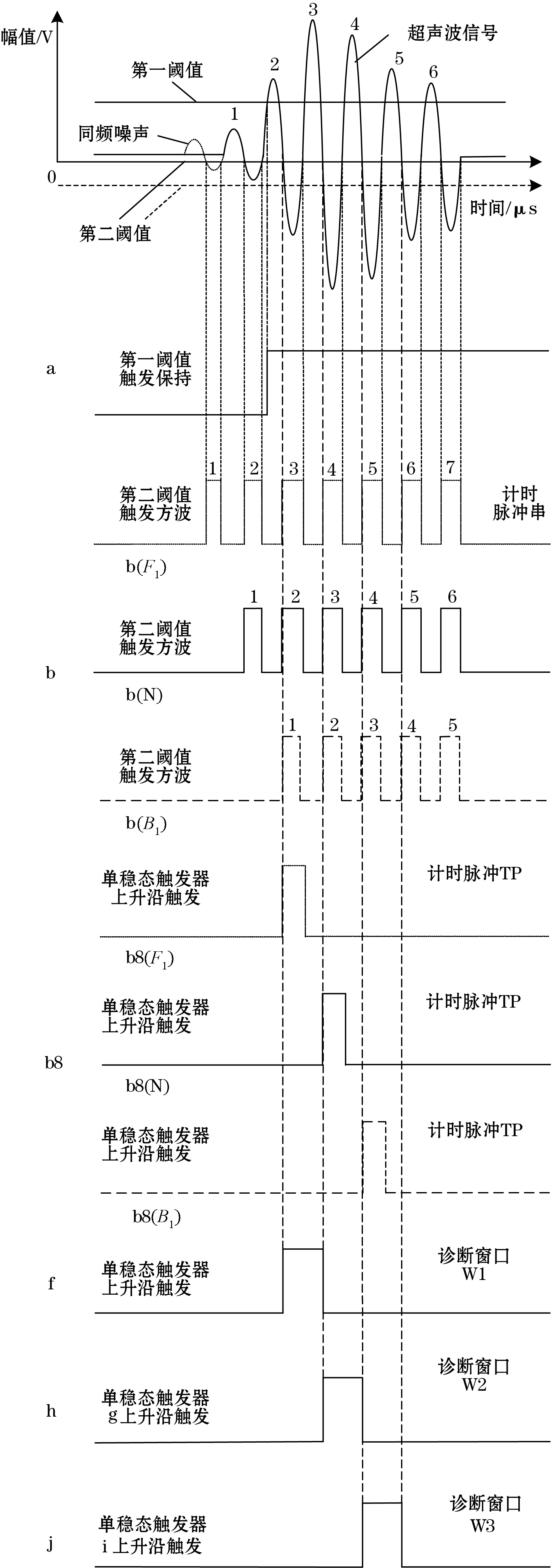
图6 跳波判断原理

当m≥2时，图4中的信号c没有发生变化，所以W1、W2、W3位置不变，而计时脉冲串较无跳波时，在前端增加了m个方波，所以TP向前移动了m个周期，较W1提前了(m-1)个周期，所以窗口均没有捕捉到TP信号，可判断为往前跳波；而当n≥2时，图7中的信号c向后移动了(n-1)信号周期，所以W1、W2、W3位置也将向后移动(n-1)信号周期，而计时脉冲串较无跳波时在前端减少了n个方波，TP向后移动了n个周期，仍然落在W3中，可诊断为往后跳波，如图7所示。因此，可依据表1第一阈值触发跳波增值表来诊断跳波情况。

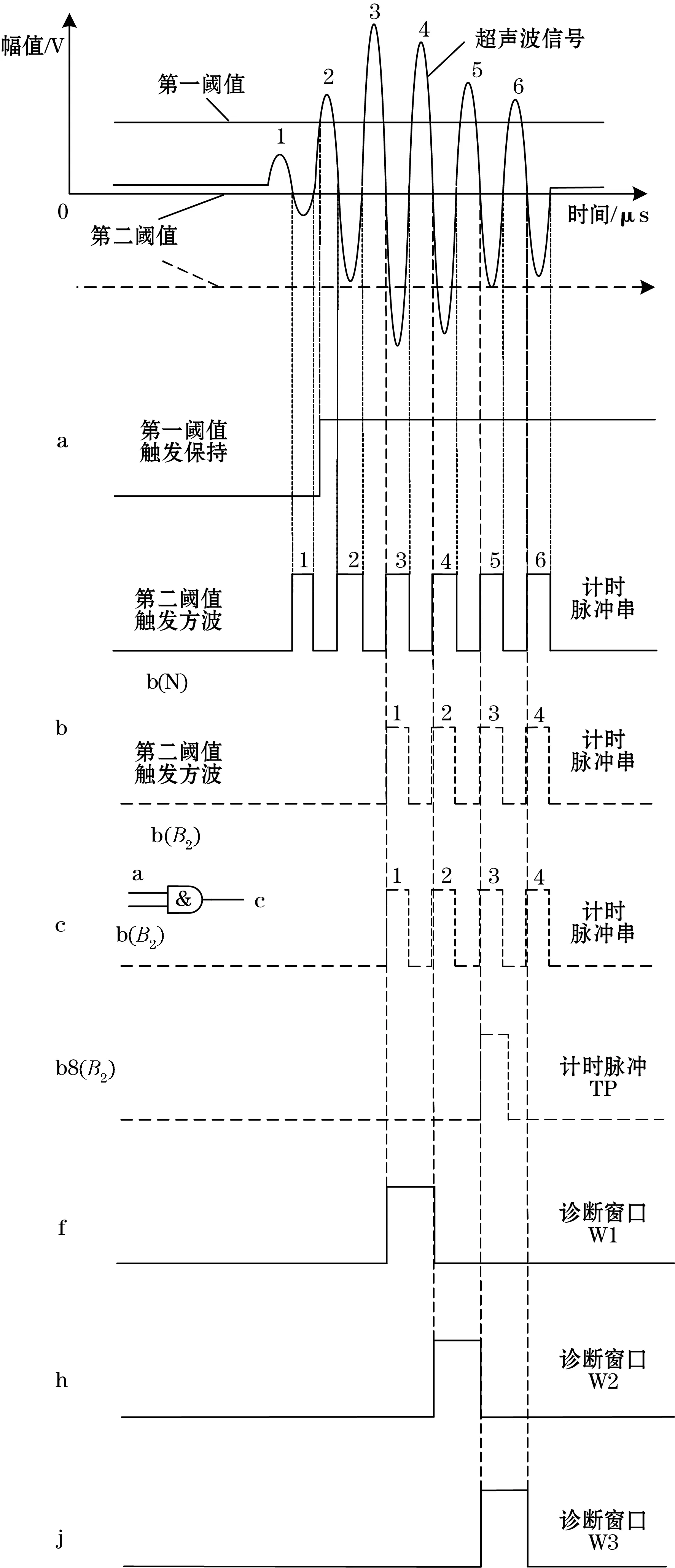
图7 往后跳2个波诊断情况

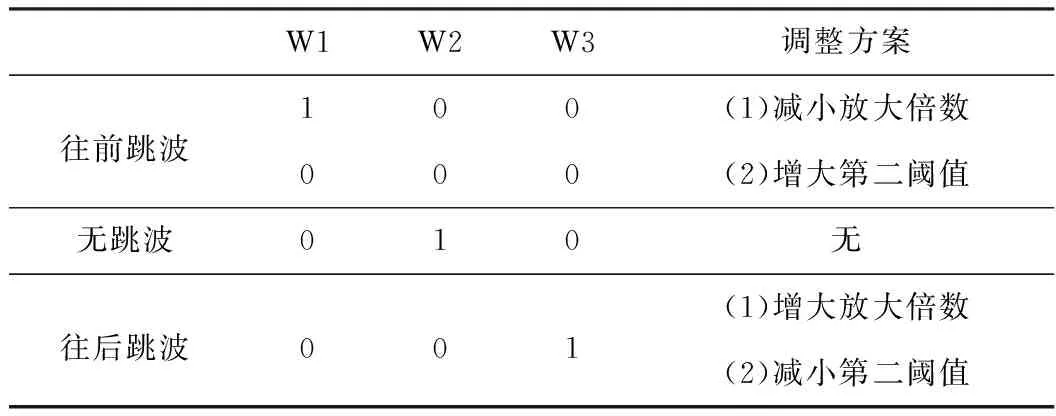
表1 第一阈值触发跳波真值表

假设第一阈值触发往前跳波的概率是10.0%，无跳波的概率是80.0%，往后跳波的概率是10.0%，第二阈值触发往前跳波的概率是20.0%，无跳波的概率是60.0%,往后跳波的概率是20.0%，那么可以得出所有9种测量情况的出现概率，如表2所示。只有出现第1、5和9的情况时，才会进入计时芯片进行计时，所以计时准确的概率可由式6计算得到：

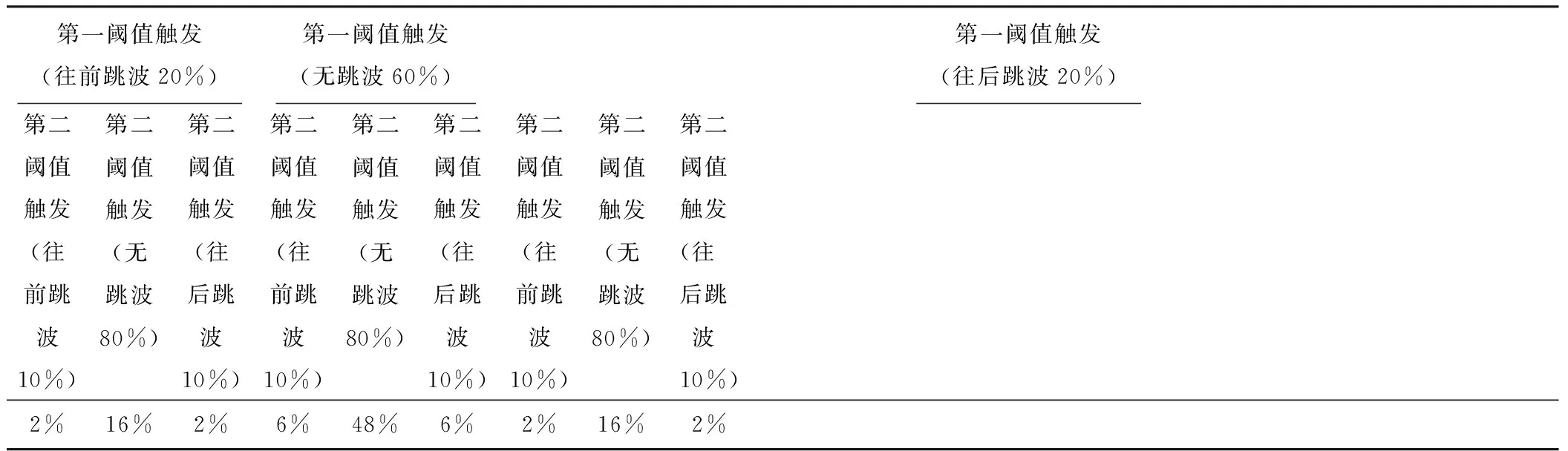
表2 9种测量情况概率统计表

(6)

测量准确率与仅用第一阈值或者第二阈值测量时的准确率比较，分别提高了12.3%和32.3%，显著提升了测量可靠性。

2 实验验证

2.1 第一阈值比例系数TFS设置可靠性验证

低功耗自诊断双阈值法的应用有个重要的前提条件，即第一阈值比例系数TFS的设置要相对可靠。也就是需要超声波信号在实际使用中，具有较快的起振速度，相邻波峰的幅值具有较大差异。由于，超声波信号包络容易受到流场和温度产生非线性的变化，因此，首先通过实验获取了所使用的200 kHz超声波换能器在不同温度(-20～50 ℃)和流量(80～800 m3/h)下的信号。温度实验平台和流量实验平台分别如图8(a)和图8(b)所示。通过实验可得如图8(c)和8(p)所示的第一阈值比例系数TFS随温度和流量变化的情况(采样周期为1 ns)。所使用换能器在测试范围内，第一阈值比例系数TFS在0.27～0.31之间变化，不容易因温度变化导致第一阈值被误触发导致跳波。

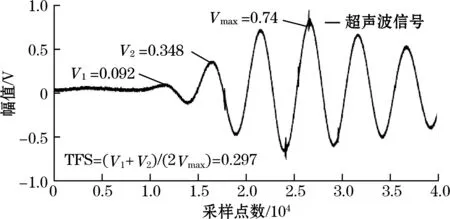
(p)阈值比例系数TFS(800.0 m3/h)

2.2 低功耗自诊断双阈值法电路设计

根据第1节，低功耗自诊断双阈值法电路如图9～图11所示。图9主要采用低功耗TDC_GP2计时芯片、低功耗单片机MSP430和相应的逻辑芯片来实现计时和诊断跳波功能。图10和图11电路主要采用低功耗比较器U1、低功耗RS触发器U2、低功耗单稳态触发器U3、U4、U5、低功耗延时芯片U6、U7和相应的低功耗逻辑芯片来产生计时脉冲串TP和诊断窗口W1、W2、W3。

(a)-20～50 ℃下阈值比例系数TFS采集实验平台

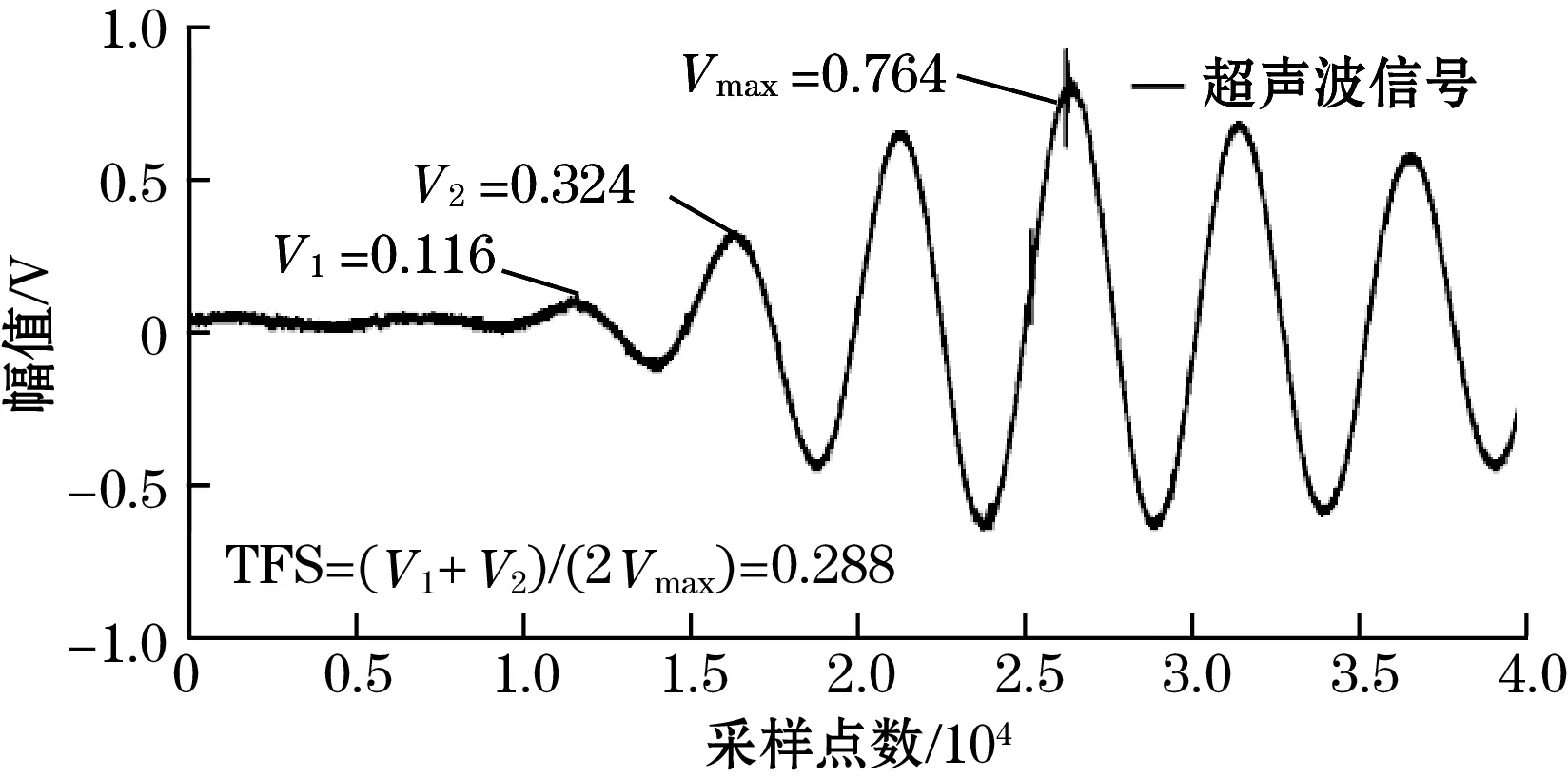
(h)阈值比例系数TFS(30 ℃)

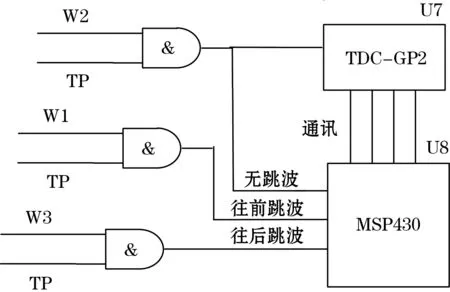
图9 计时和跳波诊断电路

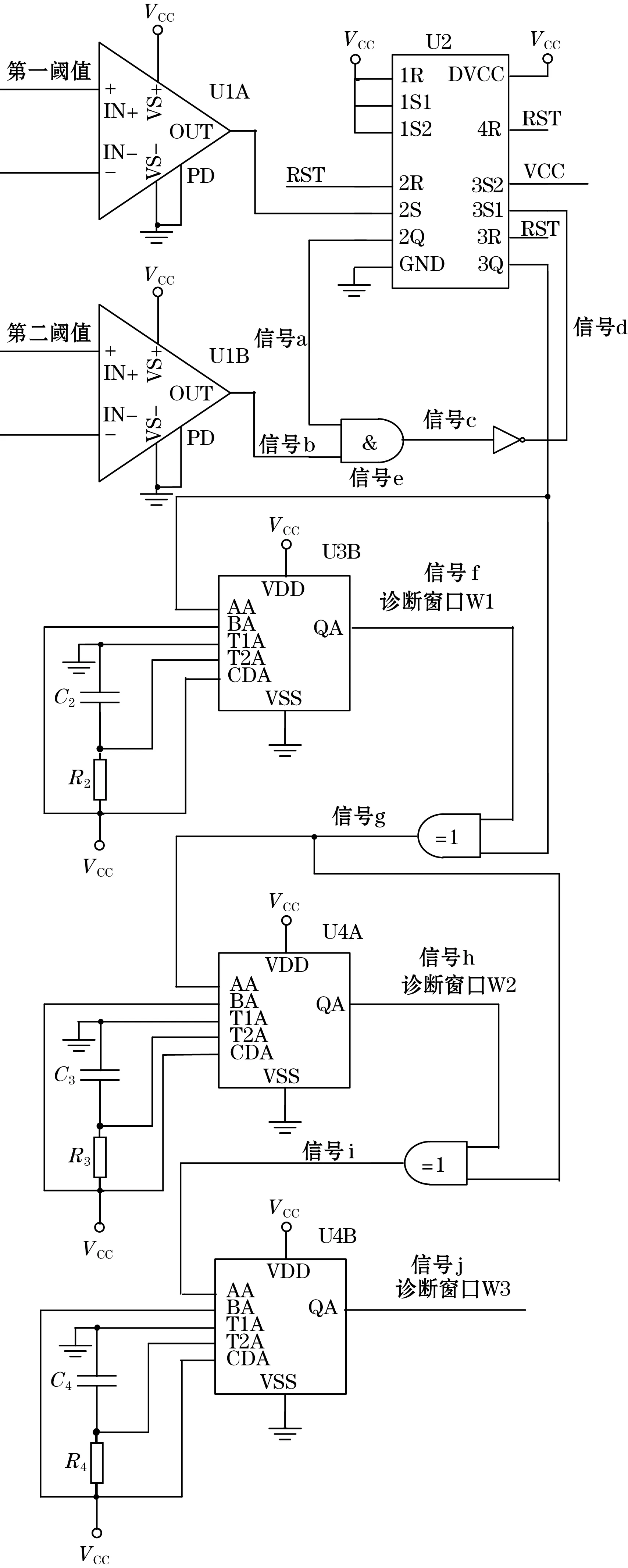
(a)诊断窗口W1、W2、W3产生电路

(a)计时脉冲TP产生电路

2.3 低功耗验证

供电电压为3 V时，低功耗自诊断双阈值法主要芯片及功耗如表3所示.若时差法流量计每次时差测量运行时间tm=0.2 s，测量间隔ti=4 s或者ti=8 s，可通过式(7)得出测量的平均电流Ii：

表3 主要芯片功耗

(7)

采用一节3.6 V-19AH锂电池供电时，其工作时长可通过式(8)得到：

(8)

式中Ii为间隔is测量的平均电流。

因此，采用4节19Ah锂电池供电，在8 s测量一次的条件下，工作寿命可长达8 a。

2.4 温度变化引发跳波的诊断实验

温度变化引发跳波的诊断实验平台如图8(a)所示，温度范围-20～50 ℃，每隔10 ℃作为1个测试温度点。实验每组测量25次，设置300组，以获得7 500个计时脉冲分布在W1、W2、W3窗口内的情况。分布示意图如图12所示，图12(a)为计时脉冲在W1内，出现往前跳波，图12(b)为计时脉冲在W2内，未出现跳，图12(c)为计时脉冲在W3内，出现往后跳波。每一个测试温度点下的7 500个计时脉冲分布在W1、W2、W3窗口内的情况，如图13所示。 跳波数据个数最多为0 ℃时，往前、往后共计17个，其余温度测试点下，均在10个以内。不仅验证了温度变化的确能导致跳波，而且通过低功耗自诊断双阈值法能有效诊断跳波情况。

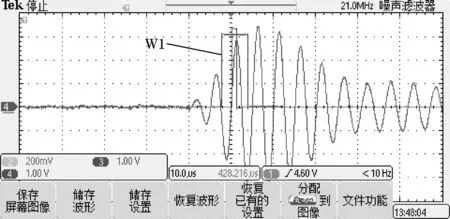
(a)往前跳波W1&TP

(a)W1、W2、W3中计时脉冲数(-20 ℃)

2.5 流量变化引发跳波的诊断实验

流量变化引发跳波的诊断实验平台如图8(b)所示。实验分为2个部分，第一部分验证0 ～28 m/s流速范围内(对应口径100 mm超声波流量计0～800.0 m3/h的流量范围)，跳波诊断的有效性。数据通过SD卡采集，跳波诊断数据如图14所示。在640.0 m3/h的流量下，未出现跳波，但是在700.0 m3/h以上尤其是流量达到800.0 m3/h时，有效诊断出508个跳波数据，而且全部是往前跳波数据，因为第二阈值相比于第一阈值更容易被触发，符合逻辑分析。

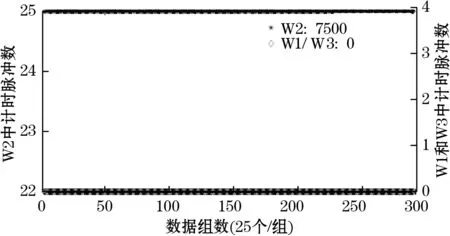
(a)W1、W2、W3中计时脉冲数(80 m3/h,200 m3/h,320 m3/h,560 m3/h,640 m3/h)

第二部分，通过标定结果来进一步验证该方法的可行性。实验根据《JJG 1030-2007超声波流量计检定规程》设置流量点以及校核相应的测量精度，最大流量设为qmax=800.0 m3/h，最小流量设为qmin=8.0 m3/h，拐点流量qmax=80.0 m3/h。根据检定规程，1级表要求拐点流量以下重复性<0.4%，示值误差<2.0%，拐点流量以上重复性<0.2%，示值误差<1.0%，测试结果如表4所示，满足上述要求。间接验证，该方法能够有效诊断跳波，滤除跳波数据，使得大流量情况下能符合计量要求。

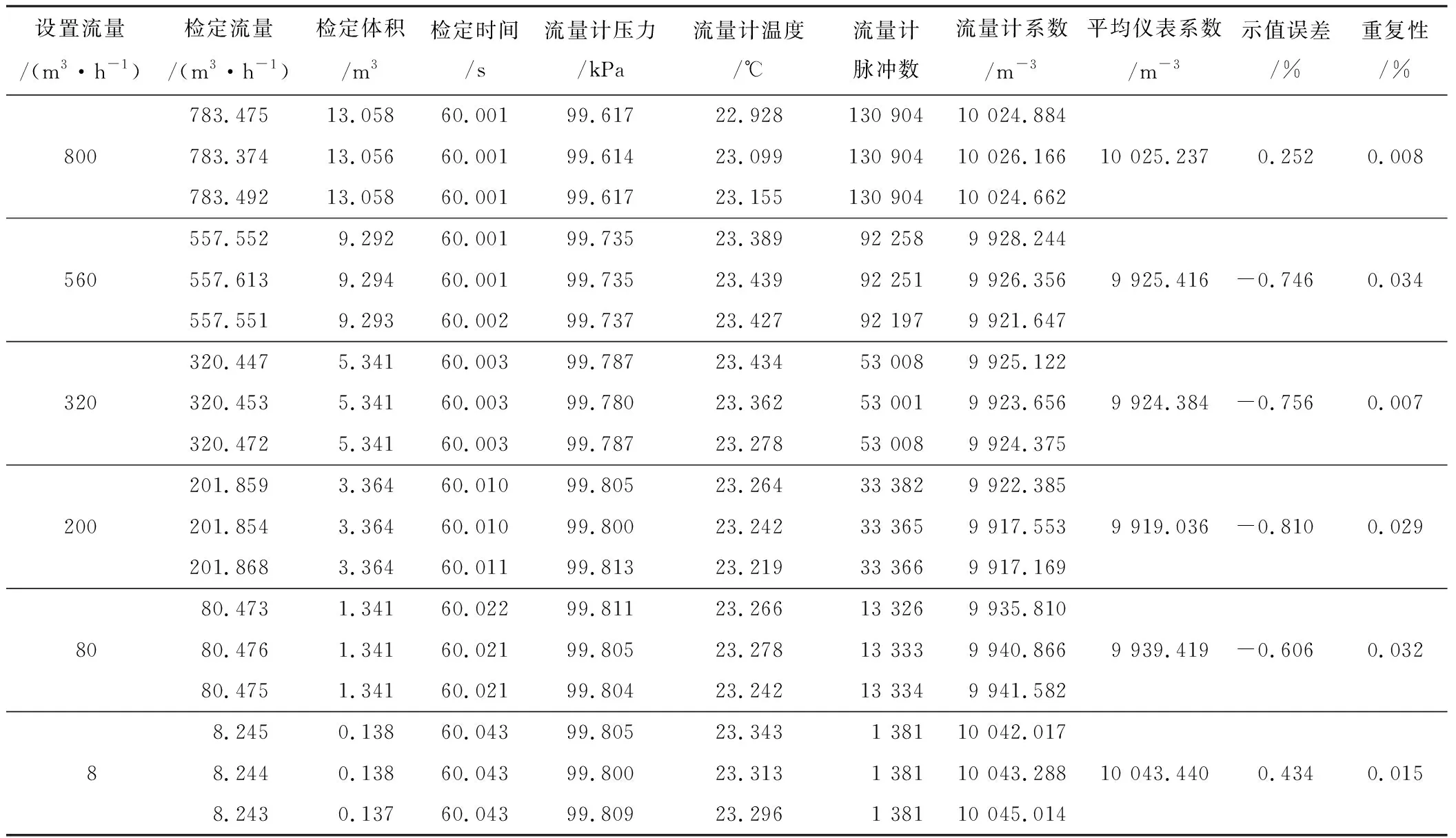
表4 口径100 mm超声波流量计8～800 m3/h标定结果

3 结论

低功耗自诊断双阈值法在传统可调单阈值法的基础上增加一个较小的第二阈值，然后通过采用低功耗比较器、低功耗RS触发器、低功耗单稳态触发器、低功耗延时芯片和相应的低功耗逻辑芯片来在保证低功耗的前提下，产生所需的计时脉冲TP和跳波诊断窗口W1、W2、W3。再然后，根据计时脉冲TP落在各诊断窗口中的情况来诊断跳波情况，当TP落在W1或者未落在任何窗口内，则可诊断为往前跳波，落在W2则可诊断为无跳波，落在W3则可诊断为往后跳波。采用上述方法的硬件测量电路，在4节3.6 V容量为19 Ah锂电池供电以及8 s测量一次的条件下，工作寿命可长达8 a。而且，通过温度和流量实验，有效验证了该方法的可行性，采用此方法的口径为100 mm的时差法超声波流量计在满足JJG 1030—2007检定规程对1级表的性能要求下，量程比达到了1∶100。

因此，低功耗自诊断双阈值法仅依靠低功耗芯片就实现了数据的实时筛选，有效抑制了跳波现象的产生，提高了测量可靠性。