数据驱动型的维修任务分配方法

摘要：采用数据驱动方法来解决维修生产环境中复杂的任务分配问题。首先利用多种细致的量化方法制订一套详细而客观的评分系统，然后采用并行计算环境下的蒙特卡洛树搜索来快速搜寻各种有价值的分配组合方案，最后从探索的树结构中选择最佳的方案来完成任务的分配。该方法不仅使数据科学技术在实际生产过程中得到落地，而且还取得了不错的效果。

关键词：数据驱动；大数定律；余弦定理；马尔科夫决策过程；蒙特卡洛树搜索

Keywords：data driven；law of large numbers；cosine theorem；MDP；MCTS

0 引言

通常在数学模型的设计上，只要数据量足够，就可以用若干个简单的模型取代一个复杂的模型，这种方法被称为数据驱动方法。该方法在数据量不足时找到的模型可能会与真实模型存在一定的偏差，但是在误差允许的范围内可以认为与精确的模型是等效的，这在数学上是有根据的。从原理上讲，类似于切比雪夫大数定律[1]，如公式（1）所示。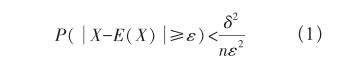

其中，X是一个随机变量，E（X）是该变量的数学期望值，n是实验次数（或者是样本数），ε是误差，δ2是方差。这个公式的含义是：当样本足够多时，一个随机变量和它的数学期望值之间的误差可以任意小。

在今天的IT领域中，越来越多的问题可以用数据驱动方法来解决。当一个问题暂时不能用简单而准确的方法解决时，可以根据以往的历史数据，构造很多近似的模型来逼近真实情况。2016年谷歌的AlphaGo[2]就是数据驱动方法对机器智能产生作用的最佳案例[1]。

1 理论分析与解决思路

1.1 理论分析

航线工作复杂多变，如果从任务序列上来审视，会发现对序列上的第n个任务如果执行了行动an（安排了具体的人员），就会导致整个团队的状态sn（员工工作量状态、人员任务的匹配状态等）发生了变化，同时这个变化后的状态sn+1又会影响到接下来的分配行动an+1，那么分配过程就可以用一条状态—行动链条[3]表示（见图1）。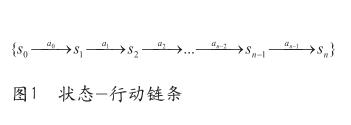

图1所示的状态序列称为马尔科夫链，这个链条包含了状态和行动的依次相互转换。如果用严谨的方式表述，策略是一种映射，它将团队的状态sn映射到一个行动集合的概率分布或概率密度函数上。可以认为管理者对每一个行动都有一定的执行可能性，且行动的评价越高，执行的概率越大，形式化来说就是在第n个任务选择最优的分配行动[3]，如公式（2）所示。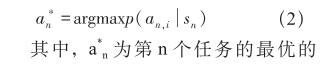

1.2 解决思路

1）状态的定义方法

把工作团队看成一个整体S，这个S的各个属性需要有客观的量化方法来计算，主要包括：人员与任务的匹配程度Sfit、人员默契程度Stacit、人為因素指标Shf、人员分配合理程度Slogic等。

2）任务分配的综合评价方法

属性指标之间关联性较强，为了保证每个指标数据都能对评估有贡献而不被稀释，采用非线性综合评价模型[5]，如公式（3）所示。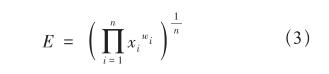

其中，E为评估分数，xi为指标量化数值，wi为该指标的权重系数。任务分配结束后计算各个属性的分值，然后汇总评估该次分配方案的分数。

3）策略好坏的度量方法

现实中不可能遍历所有的行动，根据大数定律启发，一个行动的好坏可以由其后产生的所有行动样本期望值来进行估计，并且样本数越大越接近真实值。

2 状态属性的量化方法

2.1 人员与任务匹配程度指标

Sfit指标采用余弦定理[6]来量化人员与任务之间的匹配关系。具体的计算过程可以参考笔者另一篇论文《针对大量业务数据的分析方法》[7]中的人员成分分析内容。以该任务的最优人员为基准，其他人通过计算向量角的余弦值来表示与任务的匹配程度。对已经完成的任务分配方案计算总体匹配程度，如公式（4）所示。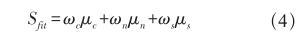

其中，ωc、ωn、ωs分别为重要任务、普通任务和简单任务在总体匹配程度中所占的比例，且ωc+ωn+ωs=100%。μc、μn、μs分别为所有的重要任务、普通任务和简单任务的配给人员任务匹配系数均值。对于VIP任务或者非常重要的任务，计算时可以对相应的人员任务匹配系数进行指数加权处理，增加系统的“惩罚”力度。

2.2 人员默契程度指标

Stacit指标与员工之间的历史合作次数直接相关，主要采用3种评判标准：1）历史合作次数np；2）近期合作次数nr；3）近期连续合作次数ns。计算时将上述3种数值和对应的权重相乘求和得到标准化的合作次数W，然后利用逻辑回归模型[6]对W进行激活处理，得到人员之间的默契程度数值，最后将各合作人员之间的默契程度数值取平均值，得到该任务的人员默契程度数值，如公式（5）和（6）所示。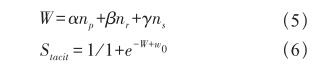

其中，α为遗忘系数（取值小于1.0），β为保持系数（一般取值等于1.0），γ为强化系数（取值大于1.0）。w0为判定人员默契的最少合作次数，该参数是超参数，可以依据现实情况自行设置。

2.3 人为因素指标

Shf指标分析人员的工作强度和间歇时间两个方面的情况。首先，将员工的普通和特殊工作时长整合为标准的工作时长Tnorm，然后通过各自的折线函数F（t）得到工作强度数值，如图2所示。间歇情况通过系数ω对工作强度数值来进行影响，ω为间歇时间满足人为因素的程度，如公式（7）和（8）所示。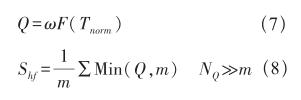

其中，Q为任务分配方案中参与人员的人为因素指标数值，对Q中m个最小值求平均，便得出了该次任务分配方案的总体人为因素指标，其中m的数值需要远小于人员数量。

2.4 人员分配合理程度指标

Slogic指标衡量员工是否有充裕时间完成分配的工作。正常生产过程中，一人同时负责多项任务或者需要跨多机位同时工作是不允许出现的状况，如果员工工作量序列中出现类似情况，就需要对任务分配方案进行“惩罚”处理。当某员工同时负责的任务个数超过设定的容忍极限值时，就直接将合理程度Slogic置0.0，若没有超过就按照超额工作时长的线性关系进行衰减处理。最后，与人为因素指标计算方法类似，取该次任务分配人员中合理程度数值最小的m个人的均值作为该分配方案的总体合理程度指标。

3 任务分配搜索方法

3.1 搜索原理

任务分配系统的核心方法是蒙特卡洛树搜索MCTS[3]，该方法大量使用于博弈类问题[8]。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡洛树搜索是一种有效的求出数值解的方法。整个过程包含4个过程，分别是选择、扩展、仿真和回传。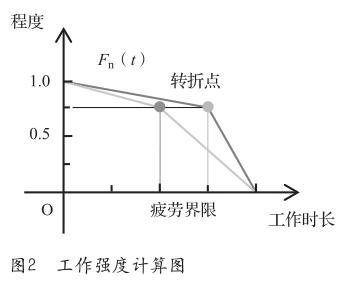

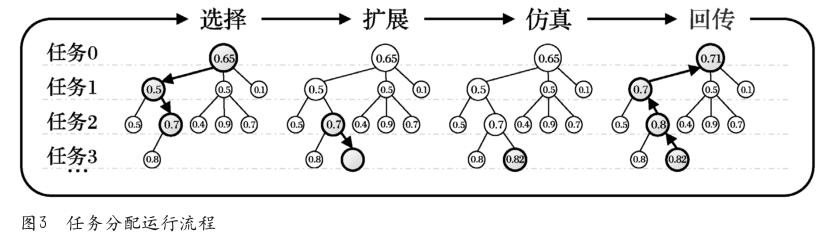
在实际计算操作过程中，任务列表按照时间顺序划分为搜索树的层级，每层的节点就是当前任务分配方法，也叫分配节点，整个搜索树的深度就是需要分配的任务数量，广度就是所有可能的方案数量，如图3所示。

按照任务的顺序从整个搜索树的根节点开始往下搜索，根据ε-greedy算法[3]随机生成新的节点或者选取最优的节点作为子节点。完成所有任务分配后，调用评估系统对任务分配方案进行打分，最后将该方案所得的分数回传到搜索树中经过的所有节点，并计算更新每个节点的回报收益均值。这种过程持续执行成千上万次，直到分配的方案分数能够满足要求或者搜索次数达到设定的数值为止。

3.2 实际应用

搜索运行过程中会面临探索和利用这一对矛盾体[3]。探索是尝试一些不同的和之前判定得分低的方案，从而增加发现更好方案的可能性。利用是指利用当前已知的情况实施策略，并把有限的采样次数尽可能地用在评价高的方案上，从而验证其有效性。

探索和利用是一对矛盾体，当计算总资源一定时，将更多的资源分配给当前表现优秀的方案就会忽略一些有潜力的方案，反之亦然。研究表明，在学习初期侧重于探索后期侧重于利用[3]具有不错的效果。本文采用UCT算法[8]来计算每个节点的置信权重，如公式（9）所示。

4 系统优化

为了提高系统的计算效率、搜索准确性和泛化能力，需要对上述运行流程进行优化设计，以便更好地应对纷繁复杂的实际生产环境。

4.1 计算效率的优化

为了提高系统的整体运行效率，缩短得到满意分配方案所花费的时间，采用了数据预存和并行计算两个方法来提高计算速度。

1）数据预存

在计算过程中其实有大量的计算是重复性的。为了提高系统的计算效率，降低系统的计算复杂程度[11]，对一些计算过程量进行存储保留，后续程序运行时可以从缓存区直接调取[11]，这样可以大幅提高程序的运行速度。

2）并行计算

Python里对应这种计算密集型的任务可以采用多进程方式来实现[12-13]，涉及多进程的运行最关键的就是整个计算过程中探索的多样性和共享数据的一致性。MCTS的几种典型并行计算方式[14]分别为：叶子节点并行模式、多搜索树并行模式、单搜索树全局锁并行模式、单搜索树局部锁并行模式。

本文采用的方式是不加锁的蒙特卡洛树搜索算法Lock-free MCTS[15]。在没有保护的计算过程中有可能导致更新信息的丢失，但是在大规模的采样环境和高效的单次搜索过程中这些影响很有限，可以被忽略[15]。

4.2 模型的搜索准确性优化

4.3 模型的泛化能力优化

1）应对航班时刻变化的能力

为了能更好地适应航线工作需求，提高模型应对复杂生产环境的能力，在计算过程中可以人為地为每个任务加入相对应的时间噪声，如公式（7）和（8）所示。

2）应对突发事件的能力

在生产中会出现某个航班的非正常滞留（如目的地机场的天气原因或航路的天气原因等）和AOG（飞机故障）情况，这些情况的出现会打乱现有的人员分配计划。如果出现类似情况，需要有对应的特殊处理方法，实际操作中的流程为：

a.从现有的航班管理系统或者生产人员那里了解航班的当前状态；

b.锁定已经处于工作中的人员分配方案；

c.更改非正常任务的工作时间范围；

d.对还未进行工作的分配计划进行清空；

e.对清空的计划任务开始新的分配方案搜索；

f.用变化小但分数高的新方案来进行人员局部调整。

5 结束语

本文的主要工作是基于强化学习的蒙特卡洛树搜索来完成任务的自动化分配。作为当前流行的机器学习方法在实际生产中的初步试探，取得了不错的效果。目前系统信息环境比较局限，可以尝试更加复杂多样的信息环境，在多个信息维度下同时展开搜索。机器学习技术落地需要不断的探索和尝试，怎样将这些前沿的研究成果转化为实际生产力是我们应该不懈努力的方向。

参考文献

[1] 吴军.智能时代[M].北京：中信出版集团，2016：30-35.

[2] SILVER D，HUANG A，MADDISON C J.，et al. Mastering the Game of Go with Deep Neural Networks and Tree Search[J]. Nature，2016（1）：484-489.

[3] 冯超.强化学习精要核心算法与 Tensorflow实现[M].北京：电子工业出版社，2018：145-147，178-181，309-312.

[4] 郭宪，方勇纯.深入浅出强化学习原理入门[M].北京：电子工业出版社，2018：18-22.

[5] 胡永宏，贺思辉.综合评价方法[M].北京：科学出版社，2000：48.

[6] 吴军.数学之美[M].北京：人民邮电出版社，2015：127-135，244-248.

[7] 陈瑞.针对大量业务数据的分析方法[J].航空维修与工程，2019（7）：52-56.

[8] BROWNE C.B.，POWLEY E.，WHITEHOUSE D，et al. A Survey of Monte Carlo Tree Search Methods[J]. IEEE Transactions on Computational Intelligence and AI in Games，2012（3）：1-43.

[9] AUER P. Finite-time Analysis of the Multiarmed Bandit Problem[J].Machine Learning，2002（47）：235-256.

[10] KOCSIS L，SZEPESV′ARI C. Bandit-based Monte-Carlo Planning[J].European Conference on Machine Learning，2006（9）：282-293.

[11] DOGLIO F. Mastering Python High Performance[M].陶俊杰，陈小莉，译.北京：人民邮电出版社，2016：12-16，84-85.

[12] BEAZLEY D，JONES B K. Python Cookbook[M].陈舸，译.北京：人民邮电出版社，2015：496-547.

[13] CHUN W. Core Python Applications Programming（3rd edition）[M].孙波翔，李斌，李晗，译.北京：人民邮电出版社，2016：122-165.

[14] CHASLOT G，WINANDS M H.M.，HERIK H J V D. Parallel Monte-Carlo Tree Search[J].International Conference on Computers and Games，2008（9）：60-71.

[15] ENZENBERGER M，MULLER M.A Lock-free Multithreaded Monte-Carlo Tree Search Algorithm[J].Advances in Computer Games，2009（5）：14-20.

[16] NELLI F. Python Data Analyt- ics[M].杜春晓，译.北京：人民邮电出版社，2016.

[17] MILOVANOVIC L. Python Data Visualization Cookbook[M].顓清山，译.北京：人民邮电出版社，2016.

[18] 贾俊平，何晓群，金勇进.统计学（第六版）[M].北京：中国人民大学出版社，2016：57-58.

作者简介

陈瑞，工程师，主要从事业务数据的分析与挖掘工作。