基于SWN-SEIRS模型的供应链金融信用风险传染测度研究

张瑞锋 李欣秋

摘 要：针对供应链金融信用风险传染问题，采用SWN-SEIRS模型进行仿真模拟分析。研究发现：SWN-SEIRS模型可以有效描述供应链金融信用风险传染路径与过程;网络规模扩大增加了信用风险传染的速度，增大了信用风险扩散范围;核心企业数量的上升虽然加快了信用风险传染的速度，但有效控制了信用风险扩散范围。这为供应链金融风险传染问题的研究方法开拓了新的思路，并为金融风险防范提供了决策依据。

关键词： 供应链金融;信用风险传染;SWN模型;SEIRS模型

一、引言及文献综述

近年随着我国支持发展供应链金融政策的实施，应收账款、存货量以及融资租赁市场的不断发展，供应链金融得到了快速发展，拓展了中小企业融资渠道，促进了中小企业的发展。据前瞻产业研究院发布的《中国供应链金融市场前瞻与投资战略规划分析报告》统计数据显示：2011年供应链金融在发达国家的增长率介于10%-30%，而在我国的增长率为20%-25%，2015年我国供应链金融的市场规模已接近12万亿元，截至2019年底，我国供应链金融市场规模已超17万亿。

供应链金融作为新兴的中小企业重要融资渠道，具有产业链、供应链、价值链多种关联属性，一旦核心企业信用出现问题，必然会随着供应链条扩散到上下游企业，影响到供应链金融的整体安全。小企业的信用风险不仅受自身风险因素的影响，而且还受供应链整体运营绩效、上下游企业合作状况、业务交易情况等各种因素的综合影响，任何一种因素都有可能导致企业出现信用风险。如何模拟金融风险在供应链的传染路径，合理测度供应链金融信用风险、控制风险，就成为商业银行业务发展的关键。

供应链金融机制中，信用风险的违约主要来自于企业自身的违约、上下游企业违约导致的交易对手风险以及违约传染。供应链金融信用风险具有复杂性、传染性、管理更严密的特征[1]。供应链金融信用风险违约传染是指供应链出现中断或宏观经济出现不利变动导致的风险，集中表现在核心企业信用状况的变化上[2]。

国外关于供应链金融信用风险传染测度方面的研究，Leung 和Kwok（2009）提出利用具有交互违约强度过程的多重债务人组合信用风险的马尔科夫链模型，分析研究信用违约互换的交易对手风险[3]。Jorion和Zhang（2009）首次提出通过直接交易对手效应对信贷传染进行研究分析，发现破产公告对债权人造成负的异常股权收益和CDS价差的增加，进一步解释了2008年雷曼兄弟破产后信贷危机突然恶化的原因[4]。Steinbacher（2013）等人提出了一个基于网络的信贷传染模型研究个别银行和银行系统的特质性和系统性冲击的影响，结果显示：特殊冲击不具有实质上扰乱银行系统的潜力，但更大规模的宏观经济事件可能具有高度的危害性[5]。Fridgen和Garizy（2015）将安全多方计算密码学方法与由社会网络分析驱动的风险识别算法相结合，在不危及企业竞争优势的情况下识别供应链网络的结构性风险[6]。Lux（2016）提出了银行和非银行企业部门之间的双部信贷网络的随机模型，实证显示：在信贷网络中，信用风险发生可能导致整个系统几乎全面崩溃[7]。Ioannis、Sumit S和Drona（2018）构建了信贷压力传播网络，并为传染性违约校准传染参数，结果显示传染效应对损失分布的尾部有显著影响[8]。Petrone和Latora（2018）引入动态PD模型研究信用风险技术和银行间暴露网络的传染机制，通过蒙特卡罗模拟得到潜在损失分布，实证结果显示银行之间的违约相关性越低，损失就越大[9]。

国内关于供应链金融信用风险传染测度方面的研究，熊熊（2009）提出了主成分分析法和Logistic 回归方法构建信用风险评价模型，用于测定风险传染的发生概率[10]。赵荣（2011）借鉴弹性系数理论构建了信用风险传染模型，研究表明只有销售价格弹性会对供应链金融信用风险传染有显著影响[11]。陈艺云（2012）提出构建了供应链金融的核心企业违约的系统性传染模型与非核心企业违约传染模型，通过仿真模拟验证了模型的可行性[12]。刘倩（2012）针对上市公司制造业的数据，采用边界Logistic模型测度供应链金融下中小企业信用风险，结果显示：相对该模型的效果更有效[13]。楊康和张仲义（2013）构建了供应链网络的风险传染模型，仿真模拟分析表明：该模型较好地模拟了风险在供应链网络中的传播深化过程[14]。王钰颖（2014）针对92家中小企业的财务数据构建了供应链金融下中小企业信用风险度量的指标模型，以酿造公司为例进行了实证分析，进一步验证了其模型的有效性[15]。陈庭强、何建敏（2014）基于行为金融和复杂网络模式构建了信用风险传染模型，结果显示社会网络结构对信用风险传染的概率有影响范围存在着显著影响[16]。陈立立（2015）采用修正的KMV模型分别对医药流通、钢铁等领域内供应链体系内上市公司的信用风险传染结果进行测量[17]。李梦宇、周莹（2015）采用信用风险结构化模型测度核心企业发生经营变故时给银行带来的风险及上游企业的传染效应，并根据违约概率计算了违约损失[18]。李永奎、周宗放（2015）构建了无标度网络的关联信用风险传染D-SIS模型，研究显示关联信用风险的传染具有延迟效应，延迟时间越长关联信用风险的传染强度越强[19]。罗刚等人（2015）基于SI传染病模型提出了担保网络的风险传播模式，根据金融机构数据的验证，发现不同的传染源对信用风险传播速度及范围的影响也是不同的[20]。苏传场（2015）提出使用SI病毒传染模型构建供应链金融信用风险传播模型，通过模拟仿真，明确了该模型的优越性[21]。曾洁（2015）运用主成分分析方法对供应链金融信用风险产生影响的决定性因素进行深入分析[22]。栗天岭（2015）提出了以核心企业的信用视角的CVaR信用风险度量模型，以汽车产业链为例，对信用风险进行了验证和预警，并提出了对策建议[23]。梁海凌（2016）对52家中小企业的应收账款数据，提出MKMV-Logit模型计算履约概率，实证显示与企业实际具有比较高的吻合性，模型的预测能力及稳健性较好[24]。孟婷（2016）以汽车行业数据为样本，运用Logistic模型测度供应链金融信用风险，并提出风险防范措施[25]。张媛（2018）提出了基于强度模型、小世界网络与SIR传染病模型，通过仿真模拟验证了模型的可行性，比较理想地测度了供应链金融网络中信用风险传染的程度[26]。陈冬玲（2018）基于复杂网络的视角提出构建了BA无标度虚拟供应链金融网络，并以SIS传染病模型研究信用风险传播过程，通过仿真模拟验证了关键性影响因素对信用风险传播的影响效应[27]。

二、SWN和SEIRS模型的基本理论

（一）SWN模型及特征

小世界网络是特殊的复杂网络结构，在这种网络中大部分的节点彼此并不相连，但绝大部分节点之间经过少数几步就可到达。20世纪60年代，美国哈佛大学社会心理学家Stanley Milgram通过“连锁信件”实验发现了小世界现象，如果来自不同群体的两个人不相识，最多只需六个朋友的介绍就能相识，即“六度分隔”理论。Duncan Watts和Steven Strogatz在1998年将高集聚系数和低平均特征路径长度作为两个典型特征，提出小世界网络模型（WS模型），为研究复杂网络提供了新的思路和方法。1999年，Newman和Watts提出了改进的小世界网络模型（即NS模型）。

1.WS模型[28]。

Duncan Watts和Steven Strogatz在规则网络中插入随机因子，构建WS模型。构建步骤如下：首先，构建一个具有N个节点组成的规则网络，每个节点有K个邻居相连。其次，随机重布线，选择一个顶点和沿着顺时针方向连接它和它最近的邻居的边，以p的概率将这条边重新连接到在整个环上均匀随机选择的一个顶点，同时禁止重复的边;否则就把边留在原处。重复这个过程，顺时针绕着圆环，依次考虑每个顶点，直到完成一圈。接下来，考虑将顶点按顺时针方向连接到其第二近邻的边，以概率p随机地重新连接这些边，绕着环循环，在每圈之后向外延伸到更远的邻居，直到原始格中的每条边被考虑一次。对于p=0，规则网络不变;随着p的增加，图变得越来越无序，直到p=1，所有的边被随机地重新连接，形成小世界网络图。

2.NW模型[29]。

Newman和Watts将一维小世界模型推广到了高维模型。

首先，每个节点与所有相邻节点连接到一定范围K内，形成一个平均配位数Z= 2K的网络。其次，通过以概率p独立地重新布线引入随机性。在这种情况下，重新布线意味着将连接的一端移动到一个新的、随机选择的位置。因此，网络的行为依赖于L（一维模型模型定义具有L节点）、K和p这三个独立的参数。对于足够小的p和足够大的L，对k=2的网络顶点之间的平均分离没有影响，对K= 1产生影响。因为原来的小世界模型定义在这种情况下有一个有限的概率成为其余的一部分，因此做出无限的贡献平均顶点之间的距离，这使所有网络的平均距离为给定值p也无限。

3.小世界网络的特征。

特征路径长度L（p），即为两个节点之间最短路径上的边数，是对所有节点的平均距离，说明联系到两个节点所需要的步数。即：

（二）SEIRS模型基本理论

在不考虑出生率和死亡率等种群动力学因素，即描述病程较短、疾病流行期内种群的出生、自然死亡可以忽略不计的疾病时，传染病模型可以分为有疾病潜伏期和无疾病潜伏期两类[30]。无疾病潜伏期的传染病模型主要有：SI模型、SIS模型、SIR模型、SIRS模型;有疾病潜伏期的传染病模型主要有：SEIR模型、SEIRS模型，两者区别在于，SEIR模型中病人康复后具备永久免疫力，而SEIRS模型中病人康复后仅获得暂时免疫（传染病模型英文缩写是指Susceptible，Exposed，Infected，Recovered，Susceptible单词形成的不同组合）。

在供应链金融体系内节点企业爆发信用风险时，由于各类企业抵御风险能力不同，在一些企业风险突然爆发时，相关联的企业即便处于波及范围，也只会成为易感染状态，并不会骤然被同化。只是经过一段时间的风险抗衡，关联企业自身防御能力被击穿后，才转而爆发信用风险，这个过程更符合传染病模型中的潜伏状态，且当一次风险过后，仍然存在信用风险再次来袭的可能，供应链金融企业并不能永久免疫风险，这两个特点决定了我们选择SEIRS模型而非其他传染病模型。

SEIRS模型是指健康者与感染者接触后由于存在一段时间的潜伏期和发病概率不会马上变成感染者的情况。基于此，SEIRS模型将人群为四类：S（t）表示易感染者，即在t时刻虽未被感染但之后可能转变为潜伏者的数量;E（t）表示潜伏者，即在t时刻已经被病毒感染但还未发病的数量;I（t）表示感染者，即在t时刻已经被感染发病且具有能力传染其他易感染者的数量;R（t）表示免疫者，即在t时刻从感染者中移除且具备免疫能力的数量。

假设整个网络中的节点总数为N（t）且在一段时间内保持不变，在t时刻，N（t）=S（t）+E（t）+I（t）+R（t）。根据SEIRS模型的基本原理，构造每类节点企业数量对应的动力学方程如下：

其中，λ表示病毒的传染率，ω表示病毒的发病率，γ表示感染者被治愈并获得免疫能力的概率，σ表示免疫者转变概率。根据SEIRS模型，传染过程主要是来源于感染者与他人的接触，感染者只能传染易感染者，使部分易感染者变为潜伏者;但是并不是每一个接触到感染者的人都会成为易感染者，这就是λ系数存在的缘由。同理，易感染者并非全部都会发病，这是基于传染病本身的性质，致使一部分人成为潜伏者发病成为感染者，而后感染者可能通过治愈获得免疫。如图1所示。

三、SWN-SEIRS模型及供应链信用风险分析

（一）SWN-SEIRS模型

在供应链金融体系内，企业间通过现金流、信息流、贸易流等方式彼此关联，一旦某方信用风险暴露，就会通过网络载体沿着关系网络进行传播，最终扩散到整个供应链金融网络。由于供应链网络符合小世界网络的特性，结合SEIRS模型，考虑供应链网络中节点企业自身差异，构建供应链金融信用风险传染测度模型，并做出如下假设：

假设1 供应链金融网络是有限闭环网络。网络中主体包括核心企业、中小企业、银行及第三方物流企业等，每个企业即网络中一个节点，在信用风险传染过程中不存在新的节点企业進入。

假设2 信用风险在供应链金融网络中的传播是一随机过程。即在网络内部信用风险传染的方向是不固定的，其向上下游企业的传播是随机的，且只要企业间产生金融业务时，则认为对应节点间建立了联系，对应边的权重随节点企业间关联强度的增大而增大。

假设3 节点接触概率假设。考虑小世界复杂网络形态，假设t时刻，某一易感染者节点与一个度为ki的节点接触概率为θt（i），则供应链网络的平均度K=∑Ni=0kiP（ki），其中P（ki）表示度为ki的节点的概率。

（二）供应链金融信用风险阈值分析

采用马知恩提出的传染病动力学方程求解方法对模型（4）进行求解[30]。信用风险传染的阈值计算过程可知，只有dS（t）dt<0时，才表示风险在向下传递，即整个体系内存在风险传染的阈值，一旦突破这一数值，信用风险才会沿网络关系进行扩散。因此，风险传染的阈值与供应链网络中所包含的免疫节点的数量无关，可以直接简化得：

则R0就是判断信用风险能否在供应链金融网络中传染的阈值，当R0>1时，信用风险会沿网络路径扩散;当R0<1时，信用风险是可以控制的，不会在供应链网络中传染，且暴露信用风险的节点企业数量也会逐渐递减并最终趋向于零。

四、SWN-SEIRS模型仿真模拟分析

（一）供应链金融信用风险传染路径模拟

为了验证SWN-SEIRS模型研究供应链金融信用风险传染的有效性及合理性，采用JavaScript编程，通过改变状态节点比例对风险传染的路径进行模拟。

假设供应链网络规模和核心企业数量对信用风险传染速度及范围均呈正向影响，即随着网络基本属性的提高，信用风险传染范围不断扩大，风险传播后达到稳态的时间逐渐增长。结合实际情况，一般供应链金融体系中至少含有一个节点度高、抗风险能力强的核心企业，参考小世界网络模拟算法和供应链金融网络特征，对模拟的初始值进行设置：网络节点N=100，随机加边概率p=0.2，初始状态时各类型节点密度为：S（0）=0.98、E（0）=0.01、 I（0）=0.01、R（0）=0，资料显示我国平均每个企业拥有4至5个战略合作伙伴，故而设置网络平均度K=4，核心企业顶点度设为10;参考SEIRS模型的参数设置，结合供应链金融网络信用风险传染的实际情况，设传染率λ=0.2、发病率ω=0.2，被治愈并获得免疫能力的概率γ=0.05，免疫者转变概率σ=0.05，t=50。

根据方程（8）得到R0=1.96，已经超过风险传染阈值1，说明信用风险会沿网络路径扩散。设横坐标是时间、纵坐标是节点企业密度，根据方程（4）模拟的风险传染显示：随着时间推移，易感染企业在风险爆发初期急剧传染并快速放缓传染速度，最后数量逐渐稳定;潜伏企业数量随着风险传染的不断扩散始终保持缓慢增加态势并最后趋于稳定;感染企业数量在风险暴发初期迅速增长，并很快达到稳定且稍有回落;免疫企业由其自身特点决定，在初期迅速爆发风险后，先缓慢增长后增速加快，最终达到稳定状态，这可能是由于风险大面积爆发时，免疫企业自身风险管理能力提高所带来的结果，如图2所示。

根据方程（1）和（2），考虑供应链网络规模N由50以间隔10增加至200、核心企业数量由2逐步增长到20时，SWN重要指标的变化见表1。可以看到，在改变网络规模时，集聚系数微微下降，这表明随着供应链规模的扩张，节点企业间的业务往来紧密程度相对降低但幅度不大;特征路径长度略微变小，则说明企业间的业务关联程度稍稍加强;而网络平均度的增加，则说明随着网络规模的增加，企业业务所覆盖的范围在不断扩大，也就是说网络规模的扩大会促进供应链金融业务规模的扩张。在改变核心企业数量时，集聚系数明显降低，说明核心企业数目增加使得整个供应链网络联系更加紧密，业务关联强度增加;特征路径长度减小，是因为随着核心企业数量的增加，关联企业个数大幅增加，网络中节点企业间的联系加强;网络平均度上升，是因为一个核心企业相关联的中小企业数量巨大，随着核心企业的增加，能够为更多中小企业提供金融服务信用支持，从而整个网络的平均度会不断提高。

（二）供应链网络规模对信用风险传染速度的影响

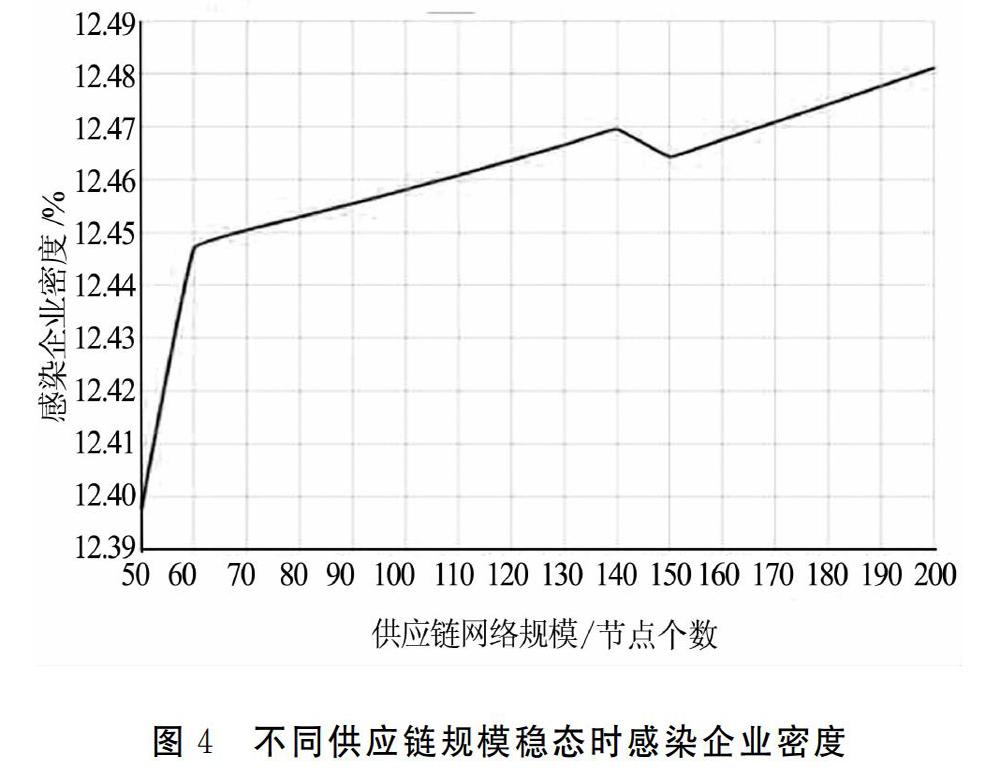
为了分析供应链网络规模对信用风险传染速度的影响，在网络规模初始值N=50的基础上，以间隔10增加到200。传染时间模拟结果显示：随着供应链网络规模的不断扩大，达到稳态所需的时间先是大幅减小进而保持不变后震荡下滑。这说明：在供应链网络规模刚刚开始增加时，由于网络平均度仍处于较低水平，各节点企业之间联系不紧密，此时信用风险传染达到稳态的时间略长;但是当网络规模大幅度扩张，随着网络平均度的增大，虽然体系内企业之间联系在加强，但变化幅度仍然低于风险传播速度，风险扩散时间震荡缩小，如图3所示。

感染企业密度模拟的结果显示：稳态时感染状态企业密度先急速上升而后增幅放缓震荡上升。这说明：在供应链网络规模刚刚开始扩大时，由于达到稳态时间骤减，使得风险传染的扩散难度降低;與此同时，网络规模扩大使得企业总数在增加，虽然整个体系中风险企业的的数量没有明显增长，但是风险传染路径更多，造成风险扩散速度更快，这就导致最终稳态时感染企业的密度在不断上升。但同时也应看到，由于网络规模改变的条件下，整个网络体系内业务关联强度变化不明显，所以感染状态企业密度在绝对数值上只是轻微上调，如图4所示。

（三）核心企业数量对信用风险传染的影响

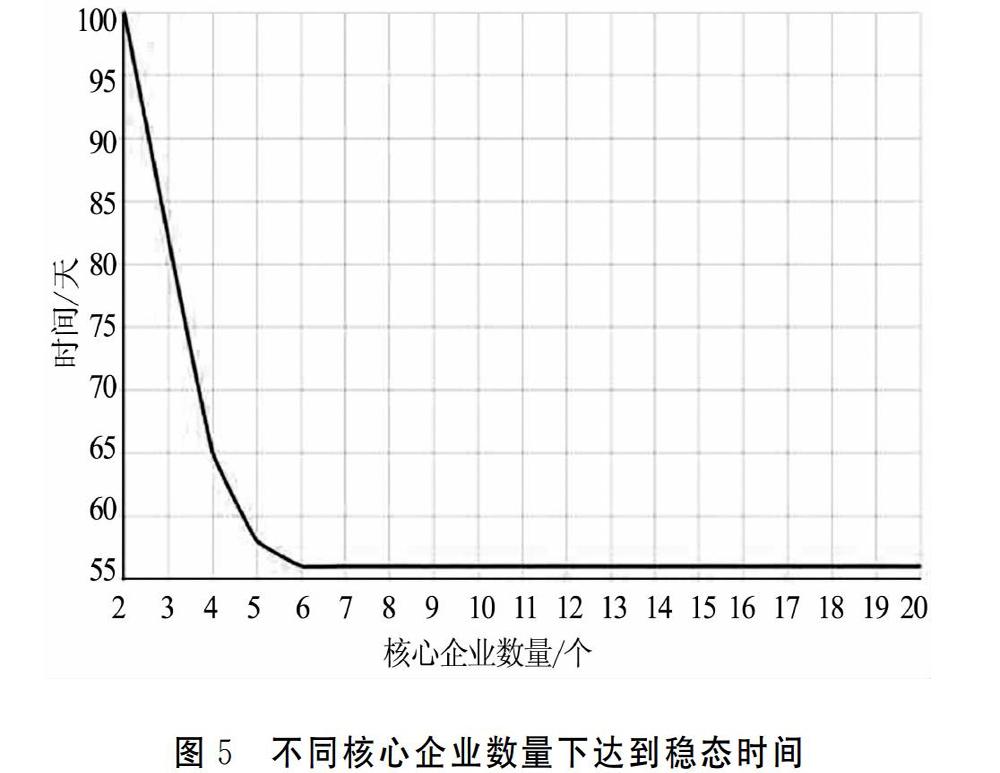
为了分析供应链核心企业数量对信用风险传染速度的影响，将初始值从2开始逐步增长到20，进行仿真模拟。传染时间模拟结果显示：当核心企业数量不断增加时，达到稳态所需的时间先急速下降后趋于稳定，这是因为增加一个核心企业，会导致增加数个与其有关联业务的中小企业，这将进一步加快风险传染速度，降低风险传染达到稳态的时间，但是当核心企业数量超过6以后，受核心企业数量的影响，网络内业务关联程度更加紧密，整个网络中风险扩散不再受限，达到稳态的时间也趋于定值，如图5所示。

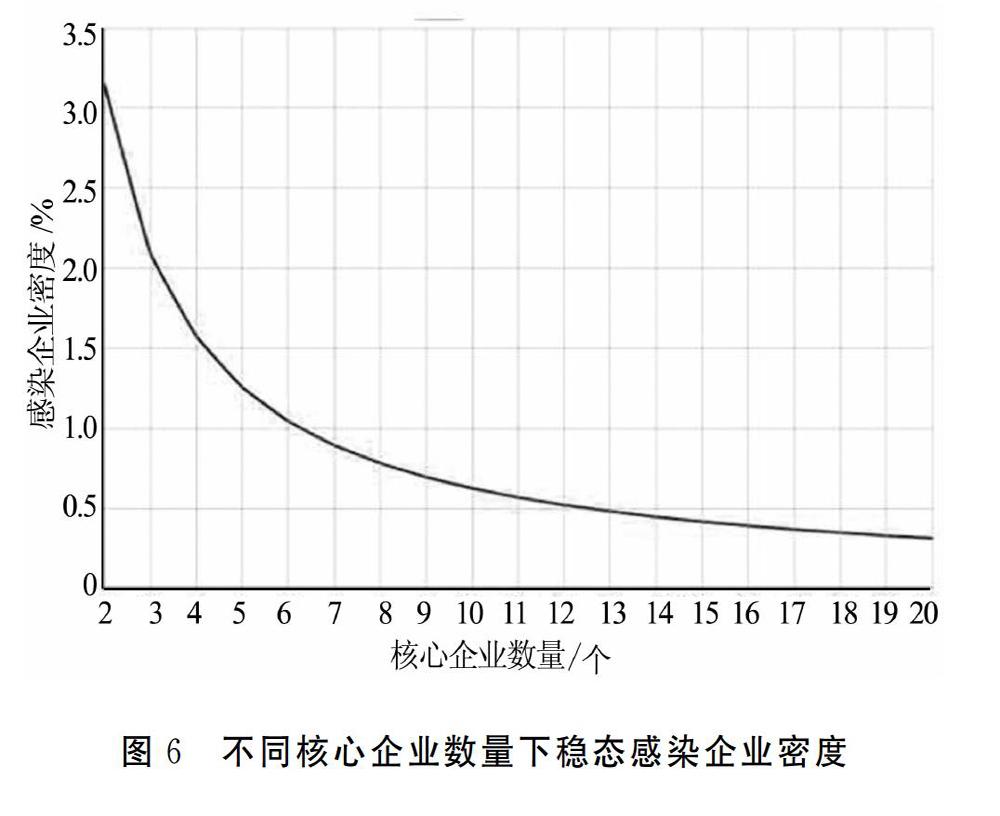
感染企业密度模拟的结果显示：随着核心企业数量增加，稳态时感染企业密度先大幅下降后缓慢降低，这是缘于虽然核心企业数量的增加使得风险传染速度加快，但核心企业本身不仅规模庞大还具备完善的抗风险能力，尽管风险传染速度加快，但同时也提高了供应链网络整体的风险免疫能力。但当核心企业数量达到一定数值后，由于牵涉的中小企业数量增加过快导致风险爆发的可能性大幅提高，核心企业的风险免疫能力也受到一定影响，使得稳态时感染企业密度下降速度放缓，如图6所示。

五、研究结论

通过对SWN-SEIRS模型研究供应链金融信用风险的仿真模拟分析，主要的研究结论有：

第一，SWN-SEIRS模型研究供应链金融信用风险的传染时，不仅通过小世界网络模型反映节点企业的关系，客观地描述其传染的路径，同时也在测度金融业务关系强度的基础上直观刻画了信用风险传染的过程，为供应链金融风险的防范提供了决策支持。

第二，供应链金融网络规模的扩大，不仅在一定程度上增加了信用风险传染的速度，同时也增大了信用风险在整个供应链体系中的扩散范围。

第三，核心企业数量的上升会提高整个体系内的信用风险免疫能力，风险扩散时间不断降低的同时，风险传播范围也在不断缩小。

第四，供应链信用风险暴发突然、传染迅速，需要一定时间才能达到稳定状态，要努力提高节点企业的自身风险免疫能力，同时发挥规模效应，积极利用核心企业的风险防控能力高的特点，从而提高整个供应链金融的风险免疫水平。

参考文献：

[1] 杨露梅. 供应链金融信用风险评价研究[D].广州：华南理工大学，2014.

[2] 陈艺云.违约传染与供应链金融的信用风险测度[J].统计与决策，2012（1）：33-35.

[3] Leung K S ， Kwok Y K . Counterparty risk for credit default swaps： Markov chain interacting intensities model with stochastic intensity[J]. Asia-Pacific Financial Markets， 2009， 16（3）：169.

[4] Jorion P ， Zhang G . Credit contagion from counterparty risk[J]. Journal of Finance， 2009， 64（5）：2053-2087.

[5] Steinbacher M ， Steinbacher M ， Steinbacher M . Credit contagion in financial markets： A network-based approach[DB/O]. SSRN Electronic Journal， 2013.

[6] Fridgen G， Garizy T Z. Supply chain network risk analysis：A privacy preserving approach[R]. 23rd European Conference on Information Systems， Münster， Germany， 2015.5.

[7] Lux T . A model of the topology of the bank-firm credit network and its role as channel of contagion[J]. Journal of Economic Dynamics & Control， 2016， 66：36-53.

[8] Ioannis A ， Sumit S ， Drona K . Incorporating contagion in portfolio credit risk models using network theory[EB/OL]. Complexity， 2018：（6076173）：1-15.

[9] Petrone D ， Latora V . A dynamic approach merging network theory and credit risk techniques to assess systemic risk in financial networks[J]. Entific Reports， 2018， 8（1）：55-61.

[10]熊熊，马佳，赵文杰，等.供应链金融模式下的信用风险评价[J].南开管理评论， 2009， 12（4）： 92-98，106.

[11]赵荣. 供应链信用风险传导机制研究[D].北京：中国矿业大学（北京），2011.

[12]陈艺云.违约传染与供应链金融的信用风险测度[J].统计与决策，2012（1）：33-35.

[13]刘倩. 供应链金融模式下中小企业的信用风险度量研究[D].哈尔滨工业大学，2012.

[14]杨康，张仲义.供应链网络风险传播SIS-RP模型及仿真[J].北京交通大学学报，2013，37（3）：122-126.

[15]王钰颖. 供应链金融下中小企业信用风险度量的研究[D].上海：东华大学，2014.

[16]陈庭强，何建敏.基于复杂网络的信用风险传染模型研究[J].软科学，2014，28（2）：111-117.

[17]陈立立，单汨源，张人龙.基于KMV和关联规则算法的行业供应链信用风险传染研究[J].科技管理研究，2015，35（13）：211-217.

[18]李梦宇，周莹.供应链融资风险传染度量及贷款利率定价[J].统计与决策，2015（20）：152-156.

[19]李永奎，周宗放.基于无标度网络的关联信用风险传染延迟效应[J].系统工程学报，2015，30（5）：575-583.

[20]罗刚，赵亚伟，王泳.基于复杂网络理论的担保网络风险传播模式[J].中国科学院大学学报，2015，32（6）：836-842.

[21]苏传场. 供应链金融信用风险评价与传播研究[D].杭州：浙江工商大学，2015.

[22]曾洁. 供应链金融信用风险问题研究[D].长沙：湖南大学，2015.

[23]栗天岭. 基于CVaR模型的供应链金融信用风险度量研究[D].河北工程大学，2015.

[24]梁海凌. 供應链金融的信用风险度量研究[D].福州：福州大学，2016.

[25]孟婷. 基于Logistic模型的供应链金融信用风险研究[D].长沙：湖南大学，2016.

[26]张媛. 供应链金融信用风险传染机理与度量[D].西安：长安大学，2018.

[27]陈冬玲.复杂网络视角下供应链金融信用风险扩散影响因素研究[D].哈尔滨：哈尔滨工业大学，2018.

[28]Watts D J ， Strogatz S H . Collective dynamics of small world networks[J]. Nature， 1998， 393（6684）：440-442.

[29]Newman M E J ， Watts D J . Renormalization group analysis of the small-world network model[J]. Physics Letters A， 1999， 263（ 4/6）：341-346.

[30]马知恩.传染病动力学的数学建模与研究[M].北京：科学出版社， 2004.

（责任编辑：王铁军）