基于水热耦合的青藏高原分布式水文模型——Ⅱ.考虑冰川和冻土的尼洋河流域水循环过程模拟

刘扬李,周祖昊,刘佳嘉,王鹏翔,,李玉庆,朱熠明,,姜欣彤,6,王 康,王富强

(1. 中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081；2. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京 100038；3. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072；4. 西藏农牧学院水利土木工程学院,西藏 林芝 860000；5. 华北水利水电大学水利学院,河南 郑州 450046；6. 中国海洋大学工程学院,山东 青岛 266100)

在对寒区水文循环进行研究时,水文模型经历了一系列的补充与完善,大多考虑了积雪、冻土影响,加入了相关计算模块,代表性的有TOPMODEL、DWHC、GEOtop模型等[1- 3],但这些模型缺少针对冰川的模拟。

在青藏高原等高寒地区,冰川、积雪作为一种特殊的固体水库,和冻土一起参与流域水循环,对河川径流的形成及变化有着十分重要的作用[4- 5]。对冰川消融的研究,按照冰川消融计算方法不同分基于温度的统计模型和基于物理机制的能量平衡模型[6]。基于温度的统计模型有冰川平衡线法和度日因子法两种:冰川平衡线法假设在特定高度上冰川的年累积量等于年消融量,以此高度处温度计算融化量[7],建立的是冰川消融时期的月平均温度与消融量间关系[8]；度日因子法以日的正积温计算冰川的融化量[9],Hock[10]和Pellicciotti等[11]为提高模拟精度,又在此基础上引入太阳辐射因子,在有实测资料的小流域地区取得了较好的模拟效果。基于温度的统计模型所需参数较少,计算简单,在缺少实测资料地区被广泛应用[12- 15]。随着典型冰川区各种自动水文、气象仪器的布设以及冰川消融理论的发展,具有物理机制的能量平衡模型也得到了不断发展,能量平衡模型把冰川表面的气象资料作为输入,基于能量平衡原理,考虑能量收支求得冰雪融化耗热量,从而计算融化量[16- 17],能够从物理机制上揭示冰川消融过程。但是由于模型输入参数较多,理论和结构较复杂,加上大部分偏远地区的冰川无法进行监测等原因,限制了能量平衡模型与水文模型的耦合[18]。近年来,部分学者也逐渐开始在现有模型基础上添加冰川模块,对高寒山区的冰川、融雪、冻土等水文过程进行模拟[19- 21],但针对青藏高原土壤层薄、下伏松散岩层厚的地质特点,在此基础上考虑冰川、融雪、冻土的高寒源区水文模型尚缺乏研究。

本次研究以冰川、积雪、冻土广泛分布的雅鲁藏布江支流尼洋河流域为研究区,基于具有物理机制的寒区水循环模型(WEP- COR),考虑“积雪- 冰川”、“积雪- 土壤- 砂砾石层”水热耦合模拟,构建青藏高原分布式水循环模型(WEP in Qinghai- Tibet Plateau模型,简称WEP- QTP模型),对尼洋河流域水循环过程进行模拟,并采用实测资料进行验证。

1 数据与处理

1.1 流域概况

选取雅鲁藏布江的一级支流尼洋河流域(图1)作为本文研究的典型区域,流域东西长约230 km,南北宽约110 km,流域面积17 535 km2。

图1 尼洋河流域基本情况

1.2 数据收集

本次研究所需的数据主要分为2类:第1类是模型计算需要的数据,主要包括地形(DEM)、气象、土壤类型、土地利用类型、植被指数和冰川面积等数据；第2类是用于模型结果验证的数据,包括尼洋河流域资料较完整的工布江达水文站2013—2016年逐月流量实测数据、泥曲水文站2013—2015年逐月流量实测数据和工布江达水文站2015年逐日流量实测数据。

在以上各项数据中,数字高程数据为SRTM90(Shuttle Radar Topography Mission),数据精度为90 m；气象数据包括逐日降水、气温、相对湿度、日照时数和风速,其中气温、相对湿度、日照时数和风速数据由流域内林芝气象站(海拔2 991.8 m)与流域外嘉黎气象站(海拔4 488.8 m)获得(图1),时间序列为1961—2018年,数据来源于中国气象数据网(http:∥data.cma.cn)；降雨数据除林芝、嘉黎2个气象站外还包括流域内工布江达、更张、巴和桥、泥曲、克拉曲、增巴在内的6个雨量站数据(2013—2015年),以及西藏水资源公报中年降水等值线图(2012—2017年),流域内气温采用考虑高程修正的RDS(Reversed Distance Squared)方法由气象站数据插值得到,降水数据采用平面插值结合降水等值线修正得到,逐日相对湿度、日照时速和风速采用RDS方法插值得到。

土壤类型数据来源于全国第二次土壤普查和《中国土种志》[22]；土地利用类型数据来自于从中国科学院地理科学与资源研究所资源环境科学与数据库中心(http:∥www.resdc.cn)收集的1980年、2005年和2014年3期的土地覆盖数据,数据分辨率为30 m；植被信息包含叶面积指数和植被覆盖度,选取2000—2017年的MODIS数据产品作为数据源,其中LAI(Leaf Area Index)精度为500 m,NDVI(Normalized Difference Vegetation Index)精度为250 m,主要用于计算蒸发和植被截流过程；冰川面积选取1988—2018年近30 a精度为30 m的Landsat TM和Landsat ETM+遥感影像(数据来自美国地质调查局USGS)作为数据源。

1.3 数据处理

(1) 单元划分。对于本次研究用到的地形数据,主要采用ArcGIS软件进行子流域的划分,提取流向、河长、坡度等信息。尼洋河全流域共划分了217个子流域,每一个子流域都根据Pfafstetter规则[23]进行编码；再根据高程将子流域划分成1～10个等高带,作为基本的计算单元,全流域共划分了871个等高带。

(2) 冰川面积空间分布。基于Landsat产品提取得2015年尼洋河流域冰川面积约760 km2,占流域总面积的4.5%。参考中国第二次冰川编目数据分条规则,结合研究区流域划分和山脊线提取结果划分冰川条目,从而实现研究区内冰川的分条面积统计；再根据子流域和等高带空间分布,将冰川面积分配到各子流域和等高带上。

(3) 气象要素空间展布。考虑到尼洋河流域地形起伏较大,气温随高程增加呈垂直条带分布,故采用泰森多边形法插值并考虑高程进行修正,获得每个等高带上的气温值；降水采用平面插值结合降水等值线修正；其他气象要素限于资料缺乏,采用反距离平方加权法插值。土壤类型、土地利用类型、植被指数等数据,通过ArcGIS软件统计到各计算单元上。

尼洋河流域等高带划分、冰川分布、气温、降水展布见图2。

图2 尼洋河流域等高带划分、冰川分布、气温和降水展布

2 模型原理与验证

2.1 模型原理

本文模型在WEP- COR模型[3,24]的基础上进行改进,WEP- COR模型平面结构和垂向结构见图3。模型在垂直结构上分为植被冠层或建筑物截留层、地表洼地储留层、包气带层、过渡带层、地下水层。其中,为体现土壤含水率从地表到深层的变化以及裸土蒸发和植被根系吸水蒸腾受土壤深度的影响,包气带土壤又分为表层、中层和底层。平面上,先把流域划分为若干子流域,再根据高程将每个子流域划分为1～11个等高带,每个等高带内再分为水域、不透水域、裸地- 植被域、灌溉农田和非灌溉农田5种土地利用类型,其中裸地- 植被域又可细分为高植被(林木)、低植被(草地)以及裸地。不透水域主要由城市建筑、城市不透水地表以及农村不透水地表组成,其中城市建筑和城市不透水地表统称为城市不透水域。灌溉农田域和非灌溉农田域具有相同的结构划分及模拟过程,差别仅在于灌溉农田域额外提供灌溉用水,作用等效于降水。水体和土壤蒸散发采用Penman公式计算,植被冠层蒸发计算采用Penman- Monteith公式。对土壤水分运动,在暴雨期采用Green- Ampt入渗模型逐小时计算；非暴雨期通过Richards方程进行逐日模拟；根据坡度和土壤水力传导率计算壤中流；地下水运动通过Boussinesq方程计算；采用运动波方程进行坡面、河道汇流模拟[25]。

本次研究为了考虑冰川、积雪和冻土对流域水循环过程的影响,增加了“积雪- 土壤- 砂砾石层”连续体水热耦合模拟和“积雪- 冰川”耦合模拟功能,构建青藏高原分布式水循环模型(WEP- QTP)。

图3 WEP- COR模型的平面与垂直结构

2.1.1 “积雪- 土壤- 砂砾石层”连续体水热耦合模拟

尼洋河流域土壤层较薄,且在土壤层下方存在较厚的砂砾石层。本文基于现场调研和观测试验构建了“积雪- 土壤- 砂砾石层”连续体水热耦合模型,模型的垂向结构从上到下分为积雪层、植被截留层、地表洼地层、土壤层、砂砾石层、过渡带、地下水含水层,详见文献[26]。

2.1.2 “积雪- 冰川”耦合模拟”

为了考虑冰川对水循环的影响,在本文模型中,将冰川从水域中独立出来,将每个等高带上的5种下垫面类型进一步分为6种下垫面类型,构建“积雪- 冰川”模型(图4),在计算的过程中,首先考虑冰川上的降雪累积与超阈值下滑,然后考虑融雪产流模拟和冰川消融模拟,同时在冰川覆盖区域忽略土壤和砂砾石层的冻融过程。冰川融水和融雪产流采用度日因子法计算,产流量直接计入到对应水文计算单元。

图4 WEP- QTP模型的下垫面划分及积雪- 冰川结构示意

融雪和融冰公式[27- 28]:

M=df(Ta-T0)

(1)

式中:M为日融雪或者日融冰量,mm/d；Ta为气温, ℃；T0为融化临界温度, ℃；(Ta-T0)为时段内正积温, ℃；df为融化系数/度日因子,mm/(℃d),单位正积温产生的冰雪消融当量。

冰川度日因子由下式计算:

df=0.009HELE-0.934BLAT-8.1

(2)

式中:HELE为海拔高度,m；BLAT为纬度,(°)[29]。

本文考虑到积雪累积、下滑和消融,计算公式如下:

(3)

式中:S为积雪水当量,mm；SW为降雪水当量,mm；SE为积雪的升华量,mm；Sd为积雪的下滑量,mm。

2.2 模型率定及验证

WEP模型的参数主要分为4类:下垫面与水系参数,植被参数,土壤参数以及含水层参数。所有参数具有物理意义,可根据观测试验数据或遥感数据来估算。对上述4类参数的敏感性进行分析[30],并根据其灵敏程度,将这些参数分为高敏感、中敏感、低敏感3个级别。高敏感的参数包括土壤厚度、土壤饱和导水系数、河床材质渗透系数等。选择高敏感参数,根据径流过程对模型进行了调试和验证。通过率定可知模型中采用的土壤层饱和导水系数为0.648 m/d,砂砾石层饱和导水系数为4.32 m/d,河床材质渗透系数约为5.18 m/d,最上面等高带、中间等高带、河谷或平原土壤层厚度分别为0.4 m、0.6 m、1.0 m。

模型率定效果标准如下:① 模拟年径流量总量相对误差(ER)尽可能小；② 模拟年径流Nash- Sutcliffe效率系数(ENS)尽可能大。计算公式如下:

(4)

(5)

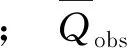
本文对尼洋河工布江达站和泥曲站2013—2016年逐月径流过程进行模拟验证,水量平衡结果见表1,模拟结果见图5,发现两站点的模拟结果与实测流量数据基本吻合,工布江达站的ENS为0.810,ER为2.8%；泥曲站的ENS为0.752,ER为-9.4%。

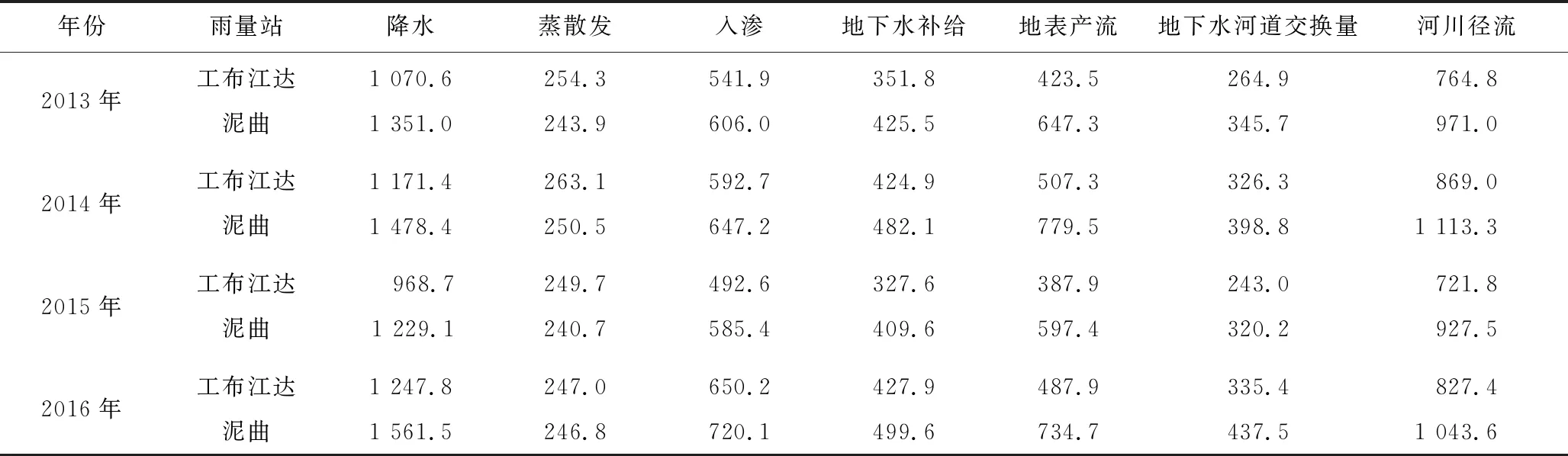
表1 工布江达、泥曲站水量收支 mm

图5 工布江达、泥曲站月流量模拟结果

3 模型效果讨论

为进一步分析本文模型模拟的效果,以2015年为例,将工布江达本文模型(WEP- QTP)与WEP- COR模型逐月流量模拟结果进行比较(图6)。相比WEP- COR模型,WEP- QTP模型在工布江达站模拟的逐月流量ENS由0.430提高到0.810,本文模型效果较好。

将工布江达水文站2015年逐日流量模拟结果与WEP- COR模型进行对比分析(图6)。由图6可见,WEP- COR模型在汛期特别是主汛前(5月冻土融化期)的流量出现大幅波动,而本文模型模拟的流量过程比较平稳,模拟效果比WEP- COR模型有明显提升,全年逐日流量ENS从-0.67提高到0.54。这主要是由于WEP- COR模型单纯考虑土壤结构,在冻土融化期土壤融化慢,受冻土层阻隔,造成河流流量峰值特别大；同时整个含水层渗透能力小,储水能力弱,造成汛期降水条件下地表产流量偏大。而本文模型考虑了土壤- 砂砾石层二元结构,冻土融化期含水层融化速度趋于正常,不易形成较大的流量峰值；同时含水层整体的储水能力和渗透能力明显提升,使得汛期产流更加平稳。尽管如此,模型改进后模拟流量过程的平稳程度仍然不如实测过程,可能与尼洋河干支流水电站的调节作用有关。

图6 工布江达站WEP- QTP与WEP- COR模型2015年逐月、逐日流量过程模拟结果对比

4 结 论

本文针对青藏高原气候和地质特点,构建了青藏高原水循环模型(WEP- QTP)。该模型在原寒区水循环模型(WEP- COR)基础上,增加了“积雪- 土壤- 砂砾石层”连续体的水热耦合模拟,同时增加了“积雪- 冰川”过程的水热模拟,使模型的物理机制更加接近于青藏高原的实际情况。

在尼洋河流域的模拟验证表明,模拟结果基本符合实际情况。与改进前的模型进行比较发现,WEP- QTP模型的模拟效果得到了较大提升。在汛期特别是主汛前(5月冻土融化期)的流量过程更加平滑,模拟逐日和逐月Nash- Sutcliffe效率系数比WEP- COR模型都有明显提升。