激光断面扫描的人造龙卷风模拟与测量

北京理工大学珠海学院 李子欣 刘炳禧 许星元 潘 杰 张锦楸

为探究龙卷风的形成原理及其气流特性，使用抽气机、鼓风机、PVC管等材料设计并制作了龙卷风发生装置，通过单片机控制步进电机驱动丝杆滑台，实现龙卷风的定距移动，并对稳定单涡旋、双涡旋分别进行测量、分析，研究了涡旋的内部结构以及对另一同向涡旋的涡旋强度的影响。

对于速度场测量方法，本文采用激光断面扫描获取图像，并利用边缘识别、计算圆隶属度的方法消除龙卷风减少不稳定造成的误差，从而得到龙卷风激光扫描断面图像之间的瞬时速度场及涡量场等数据。本文对速度场和涡量场进行了可视化，证明了装置设计思路的可行性。并进一步根据指数模型，对龙卷风风场进行二维重建，描述了人造龙卷风运动情况。

本装置还可在原来基础上增加2号龙卷风，进行涡旋之间相互影响的数值分析，有助于进一步探究、量化双涡旋的相互影响机理。

1 研究背景

龙卷风是一股激烈旋转并从快速对流的云层底部下垂循环到达地面的柱状涡旋，在我国是比较罕见极端天气，但由于其破坏力极大，并且非常难以预测，一旦出现龙卷风将难以避免很多可能出现的重大损失。当前我国对此方面的研究比较少，更多的是对台风的研究，但探讨龙卷风的同时，实际上也对台风的研究有一定的帮助。

2 设计思路

上升气流和水平剪切力是龙卷风形成的两个必要条件，特别是需要强劲的上升气流。在龙卷风形成之前，水蒸发成水蒸气先上升到天空后冷凝成云团，高空云团温度相对较低，龙卷风形成的中部水蒸气持续冷却导致体积缩小形成压差，四周的空气持续地补充缩小后的空间，加上地转偏向力的影响，龙卷风在旋转中内拢形成漏斗状，龙卷风的气压差值逐渐增大到气压梯度与运动产生的力达成平衡状态。

为模拟龙卷风内部结构，本文根据龙卷风生成的基本条件，用管道抽风机、鼓风机、PVC管及其转接键、超声波雾化器、铝架、紧固件、光轴及导轨、光轴固定座、片光发生器、高速摄影机、水槽等材料，自制了一台龙卷风发生装置，并用激光对龙卷风断面进行扫描，再利用高速摄影机采集数据，对图像进行测量计算，绘制出速度场矢量图，涡量场云图等的分析图像。

3 工作原理

底部的超声波雾化器使水转换成水雾，并通过装置顶部的抽风机制造一个低气压区，模拟地面水吸热上升到天空蒸汽层的过程。装置中部的PVC管模拟地转偏向力，使之形成垂直漩涡并提高漩涡中心的真空度，将水雾吸出后形成一根管状的漩涡。装置上部设置可移动导轨，架在支撑装置铝架上，通过光轴带动中上部的装置移动，从而实现涡旋的移动。用片光发生器水平的对涡旋断面进行扫描，可以清楚观察到涡旋的剖面，具体效果如图1所示。

图1 实际工作的效果图

4 基于ParaPIV的数据处理

通过预实验，发现得到的图像存在两个可能影响速度场计算的主要干扰因素：龙卷风的位置并不是完全稳定的，会不可避免会出现随机方向的小幅度位移，外界气流的不确定性导致龙卷风的内侧圆形真空区域并不能永久性的保持圆形，但当龙卷风稳定时，风眼的形状接近于圆形。

为了解决以上问题，本文利用MATLAB编程，识别风眼轮廓识别和计算圆隶属度评价其稳定性，可利用对龙卷风的中心点进行定位，也可利用其去除龙卷风发生微小位移时产生的误差，若进一步改进，也可用来计算龙卷风的整体位移速度；而对内部轮廓进行圆隶属度计算，则可以对图像中的涡旋进行稳定性进行评价。

4.1 速度场、涡量场分析

利用片光扫描流场，配合高速摄影机和MATLAB处理，获取每一帧图片的像素信息，然后对每两帧邻近照片的图像信息，对图像进行滤波、轮廓识别、圆心选取等的方法进行降噪，通过一系列的相关性计算，得到各个时刻近似的速度场、涡量场。

进行轮廓识别和计算圆隶属度选取圆心，用ParaPIV处理速度场计算采用MATLAB中的实现，处理后的一组图像导入ParaPIV，获取每一帧图片的像素值，对每两帧邻近照片的图像信息进行相关性计算，得到各个时刻近似的速度场和涡量场，如图2和图3所示。

图2 速度场矢量图

图3 二维涡量场云图

理论上，由于涡旋旋转运动产生离心力的原因，涡旋离心力和压差力的平衡点位于最大速度附近。但摄像头拍摄范围有限，只能拍摄到平衡半径以内的区域，导致自由涡与强制涡的边界不明显，但依然能够验证涡旋的内部结构。

4.2 二维指数风场模型

由于PIV获取的数据为像素值，而像素值与速度成正比，控制相机的拍摄角度不变，通过拍摄单一流场速度的像素值并用风速仪测出单一流场的速度，多次测量，得到像素值与速度的换算比例，即可算出涡旋的旋转速度。

通过改变鼓风机的风速，多次改变风机的档速，改变其涡旋角速度，利用PIV结合风速计校正，测得涡旋初始角速度：

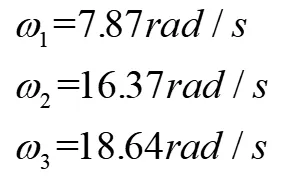
龙卷风中心气压差不变，通过不断变化其径向速度，可以发现涡旋旋转速度逐渐加快，但趋近稳定后，继续增加其径向速度，涡旋愈发不稳定。通过观测，发现在ω1=ω2的时候，更容易观测到涡旋的运动通过观测。ω2的数据如表1所示。

表1 角速度随半径变化数据表

参考指数风场模型，对龙卷风的速度场进行处理，利用指数风场对数据进行拟合，初步得到了龙卷风关于最大速度和最大半径的任意时刻的速度计算通式：

其中，V为平均半径的速度，r为距离涡旋圆心的半径。先利用高次非线性模型对数据进行拟合，求得Vmax和R。利用指数风场模型对数据进行处理，得到了α和β的值，求得：Vmax=0.61 m/s，R= 0.04 m，α=0.43，β=0.81，二维流场重建完成。

4.3 涡旋间相互影响

根据藤原定理，双台风在慢慢靠近的过程中，会受到彼此间的相互影响。通过同样采用PVC管和抽气机的组合，在另一侧添加一不可动的2号龙卷风发生装置，放置一稳定的龙卷风，调整切向风方向，使两个涡旋方向相同。初始时两涡旋涡心距0.78m，缓慢移动原来的龙卷风，渐渐靠近2号龙卷风。在此过程中选择其中5个位置用摄影机连续拍照，测量涡旋平均角速度，得出涡旋处于不同位置时的平均角速度分别为：17.9rad/s，12.8rad/s，

11.9rad/s，9.70rad/s，7.81rad/s。

根据双台风效应，两个同方向涡旋相互靠近时，会因相互干扰而强度减弱，使内侧转速减小。由此可得我们建立的双涡旋仿真模型符合实际。

5 结论

（1）通过模拟大自然龙卷风，发现形成稳定的龙卷风有三个必要条件：水平方向剪切力、垂直方向气压差、合理的吹吸比。满足这三个条件才能形成涡旋的区域，龙卷风风场具有向内辐合的流动的特性，且涡量逐渐向内传递、向外耗散，在上升气流与重力的共同作用下拉伸最终形成一个漏斗状的柱状涡旋，由于龙卷风旋转，屏蔽了外界大部分的扰动气流，中间受到的空气阻力非常小，因此可以产生更快的速度。

（2）通过数据分析，我们初步得出结论：当涡旋速度场分布在涡环中心内部，速度与半径成正比。当涡旋速度场分布在涡环中心外部，速度与半径成反比，符合大自然龙卷风的特性。

（3）通过改变水平方向剪切力的径向风速，涡旋旋转的速度逐渐增强，因此获得其不同风速的数据。龙卷风中心吸力和上升风速保持不变，通过不断变化其径向速度，发现涡旋旋转的速度逐渐加快，但趋近稳定后，继续增加其径向速度，涡旋愈发不稳定。