应用于图像分割的卷积神经网络参数简化模型

孙双林，杨 倩，张优敏

（重庆工程学院 软件学院，重庆 400056）

近年来，机器学习在图像分析领域取得了大量的成功，特别是在图像分类［1］、基于语义的图像分割［2］等领域，深度卷积神经网络（deep convolutional neural network，DCNN）成为最受欢迎的方法之一［3］。

传统的图像切割基于图切割技术，图切割就是移除一些边，使得2个子图不相连；图切割的目标是，找到一个切割，使得移除边的和权重最小。该技术的优点是分割效果还不错，并且是一种普适性的框架，适合各种特征。其问题主要在于时间复杂度和空间复杂度较高，需要事先选取分割块的数目［4］。FCN［5］是一类基于神经网络的图切割算法，它把所有的全连接层换成卷基层，原来只能输出一个类别分类的网络，可以在特征图的每一个像素输出一个分类结果［6］。Mask r-cnn［7］是一种基于划分区域的卷积神经网络的图像分割算法，该算法采用多分支输出和二进制掩码，取得了较好的分割效果，但复杂度较高。

在DCNN中，输入图像于中间层图像在大量后续层中于学习到的核心进行卷积，从而使网络可能学习到高度非线性的特征［8］。随着Tensor-Flow和Caffe等开源平台和工具的普及，DCNN的应用仍有进一步上升的势头［9］。

在DCNN应用中，为了取得更高的准确性，往往需要和其他操作相结合，比如通过缩小和放大操作，在不同的图像比例下捕获特征［10］，并且DCNN往往需要大量的中间层图像和大量可被训练的参数，对于高度非线性的困难问题，甚至需要上亿的参数［11］。复杂的模型和大量的参数给DCNN的应用带来了重大的挑战，比如层次和连接组合的不同选择可能显著地影响训练出的网络的准确性，而什么样的组合是最优的，在模型中是很难预测的［12］。此外，大量的参数还要求我们在选择超参数时必须非常小心，否则就会导致过拟合、梯度消失和时间开销过大等问题［13-15］。

为了便于DCNN的部署、训练与应用，本文提出了一种新的卷积神经网络模型，该模型中，网络的所有层都使用相同的操作集，并以相同的方式相互连接，因此无需为特定问题选择要使用的操作和连接。模型使用扩展卷积而不是缩放操作来捕获不同图像比例的特征，在一个层中使用多个比例，然后在其他层中使用密度连接媒体图像。此外，本文提出的网络体系结构以相对较少的中间图像和参数实现精确的结果，从而在训练中避免了调整超参数和额外的层的工作。在训练中，网络将学习为给定问题使用哪种扩展组合，从而可以应用相同的网络去解决不同的问题。

1 深度卷积神经网络

在本文中，模型将被应用于实值二维图像分析问题。我们将图像定义为包含m行、n列和c个通道的像素的集合，x∈Rm×n×c，并用xj表示只与通道j相关的像素x。大多图像处理问题都可以定义为对于给定图像x，寻找生成图像y的方程映射f∶Rm×n×c→Rm′×n′×c′的过程，当然输入图像和输出图像的维度可以不同。本文面向图像分类问题中，主要考虑m＝m′，n＝n′，也就是像素对像素的问题。

1.1 卷积神经网络

卷积神经网络通过互相连接的连续的多层对映射函数f建模，对于任意第i层，将以前zi-1层的输出作为输入，生成一个输出图像的特征映射zi∈Rmi×ni×ci，并且zi层输出与zi-1层输入的维度可以不同。最初的输入图像x可以作为第一层（z0），最后一层的输出将是最终的图像y。每个独立的层可以包含多个操作，通常，层的架构是：首先将每个输入的特征映射与不同的过滤器做卷积；然后将逐像素卷积的结果相加，并在结果图像中加入常量（偏差参数）；最后对每个像素做非线性运算。这些操作可以采用不同的过滤器和偏差值重复执行，从而为输出映射产生多个通道。因此，对于通道j，卷积层的输出可表示为：

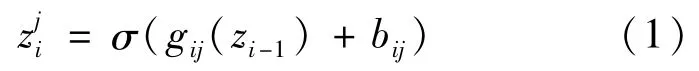
式中：σ∶Rmi×ni→Rmi×ni代表非线性运算，例如可以是sigmoid函数或rectified linear unit（ReLU）［16］；bij∈R是偏差参数；gij∶Rmi-1×ni-1×ci-1→Rmi×ni通过不同的过滤器将输入特征映射的每个通道卷积，并逐像素求合，过程为：

式（2）中，Cha代表2D图像a与过滤器h的卷积。

对于卷积过程中图像边界的处理可以采用多种方法，本文将采用反射边界。通常情况下，过滤器hijk相对较小，例如3×3像素，以使计算和训练的时间开销都较小。符合这种架构的2层卷积神经网络结果如图1所示。

图1 2层卷积神经网络架构图

1.2 DCNN

深度卷积神经网络的架构与经典卷积神经网络类似，但它包含更多的层。此外，在DCNN中通常会包含层与层之间的增大和缩小操作，并通过增大或降低特征映射的维度，以便捕捉不同规模图像的特征。很多深度神经网络会在同一层的前一半逐渐缩小特征映射，在后一半逐渐增大特征映射，这2个过程通常也叫做编码和解码。图2为基于编-解码的DCNN的架构。

图2 基于编-解码的DCNN架构

通常，随着层数的增多，DCNN比传统卷积神经网络的训练更难，因为训练将陷入局部最优并导致梯度过大或过小。此外，过大的参数空间会使训练更加困难，因为一方面时间开销更大，另一方面网络的最大似然更容易过拟合［17］，因此，DCNN往往需要巨大的训练集。为了克服这些问题，学者们对传统方法进行了一系列的改进，例如对层做归一化的批处理、层高速连接、剩余连接和分形网络等等［18-20］。虽然这些工作在某些方面取得了进步，但这些方法在很多领域难于应用，本文提出的算法能很好解决上述问题。

2 模型与算法

本文目标是通过低复杂度的网络架构得到易于在各个领域部署的深度卷积神经网络，从而显著降低参数规模和训练的难度，并能使模型自适应地解决复杂问题。为了达到这一目的，我们引入了“混合规模密集型”的网络架构概念，一方面在每层混合不同的规模，另一方面让所有特征映射密集联系。

2.1 混合规模

现有的DCNN模型大多使用扩大与缩小原则或者说编码与解码模式，与现有DCNN模型不同的是，混合密集型架构基于扩大的卷积操作，扩大卷积Dh，s在s∈Z+上利用扩大的过滤器h，h只在距离为像素s到中心点的整数倍时非零。我们通过式（3）所示的扩大方程为特定层的输出图像的每个通道连接卷积操作，即：

混合规模架构如图3所示。

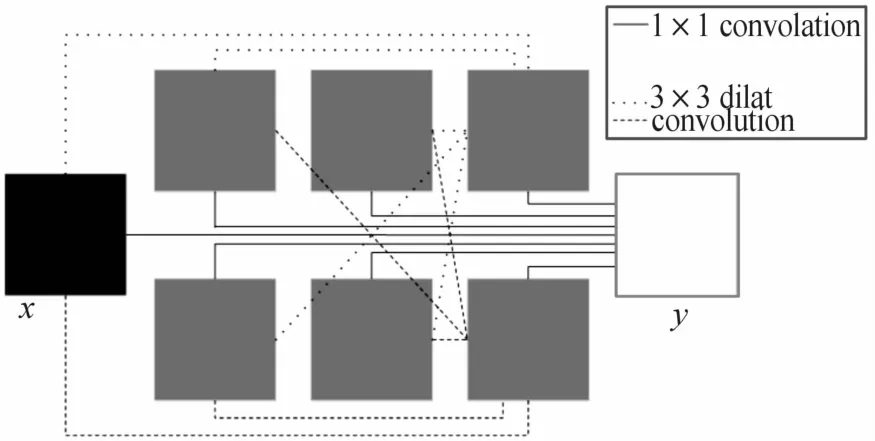
图3 混合规模架构

在图3中，可以通过多种不同的方法选择每层通道的数量，例如，可以让每层的通道数相同，都具有w个通道，网络的非输入层和非输出层的数量用网络深度d表示，在图3中我们选择w＝2，d＝3。图3中的混合尺度方法可以减轻或避免编码-解码方法中的很多不利。首先，通过大尺度的扩大，图像的大规模信息在网络的早期层就快速可得，这可以使后续层利用该信息提升性能。其次，特定尺度的信息可以直接被其他尺度利用，不再需要跨层传输，因此在训练过程中不需要学习额外的参数，从而控制网络的复杂度。此外，虽然扩大因子sij必须提前选定，但网络可以在本轮学习中确定下一轮的因子，从而自适应地应用于各种问题。

2.2 密集连接

当使用带有反射边界的卷积操作时，与传统DCNN相比，混合尺度方法还能带来额外的好处，比如：对于输入和输出图像，所有的网络特征映射将具有相同的行数和列数，也就是说对于第i层，满足mi＝m，ni＝n。因此，当计算特定层的特征映射时，不再局限于仅仅使用前一层的输出，而是所有之前计算出的特征映射｛z0，…，zi-1｝，甚至包括输入图像x，都可用来求解zi。因此，我们可以将式（1）和式（3）转化为：

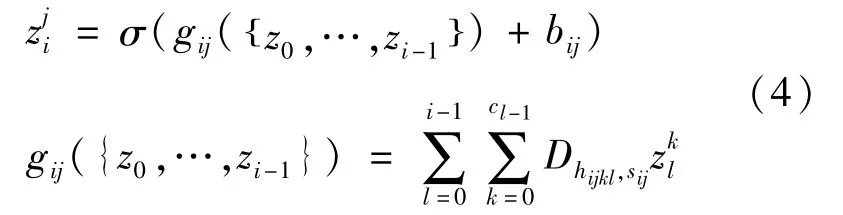
在密集连接的网络中，所有特征映射的利用与再利用都将被最大化。如果在特征映射中发现了某个有用的特征，它不需要像传统DCNN那样被其他层复制。因此就可以显著减小待训练参数的数量。

2.3 基于混合规模和密集连接的神经网络

通过将混合规模架构和密集连接相结合，我们提出了一种新型的深度卷积神经网络，本文称为参数简化型DCNN。与现有的模型类似，参数简化型DCNN也包含多层特征映射。每层特征映射都是之前所有层执行方程（4）的结果，也就是通过3×3像素过滤器扩展卷积运算、逐像素求和、为每个像素添加偏差常量矫正以及通过ReLU运算求最终解。最终输出图像的通道是通过对所有特征映射的所有通道做线性聚合而得到的，即：

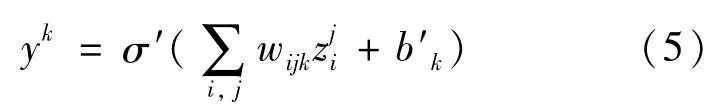
在式（5）中，对于每层中通道数量的选择可以有不同的方法，在本文中，我们采用简化的方法，让每层的通道数相同，用网络的宽度w来表示，而非输入非输出层的数量由网络的深度d表示。模型将在训练中学习方程（4）中的卷积过滤器hijkl、偏差bij和式（5）中的权重wijk以及偏差b′k等参数。当给定了网络的深度d、宽度w、输入通道数量cin和输出通道数量cout时，可以训练的参数数量Npar＝Nflts+Nwgts+Nbias，即：

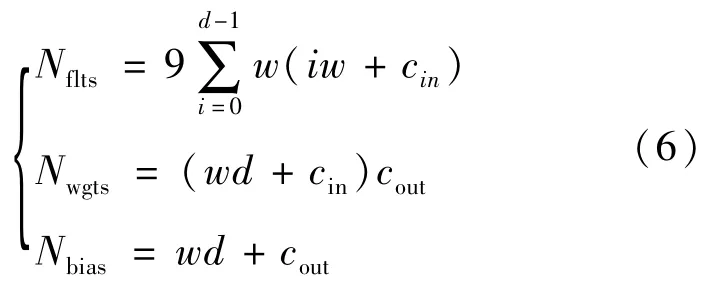
在学习过程中，我们采用均方对数损失函数作为参数学习的损失函数。根据以上分析可知，求解参数Nflts的时间复杂度为O（d），因而训练参数Npar的复杂度也是阶的O（d）。

与现有的DCNN模型相比，基于规模扩大与密集连接的参数简化神经网络具有更少的参数，可以使参数训练更加容易，并在一定程度上避免了过拟合。

3 实验与分析

3.1 实验部署

本文提出的模型通过Python实现，借助PyCUDA［21］实现GPU加速，以应对卷积等高计算开销的任务需求。现有的平台工具（如TensorFlow或Caffe等）不能实现本文提出的模型，因此本文独立地从代码上实现了本文提出的模型。模型的运行基于4颗Nvidia Tesla K80 GPU，运算平台基于CUDA 8.0。

通常，深的神经网络会比浅的网络更能得到精确的结果，并且由于本文提出的规模扩大密集连接网络的特性，应当能够得到很深的网络层次和较少的通道数量。一般的很深层次的网络总是比浅网络更难训练，但是在本文提出的模型中不存在这样的问题。我们通过对均值为0、方差为的正态分布随机采样来初始化卷积过滤器的参数，其中nc与特征映射中所有入连接与出连接之和相关，可以通过nc＝9（cin+w（d-1））+cout求得。其他可训练的参数都初始化为0。此外，在绝大多数实验中，我们使用相同分布的扩大参数sij∈［1，10］，对于第i层、通道j，sij可由式（7）求得，即：

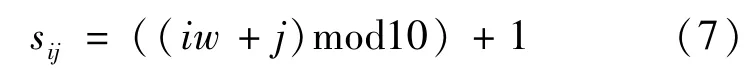
在具有L个标签的图像分割问题中，我们用L通道的图像表示正确的输出，在通道j中，对于分配给它的像素将被置为1，对于其他像素将被置为0。在最终输出层，我们用soft-max激活函数和ADAM优化方法［22］来训练，以最小化正确输出与网络输出之间的交叉熵。为了验证本文提出方法的性能，我们采用了全局准确率测度和经典准确率测度［23］。

3.2 实验与仿真数据

在第一个实验中，网络输入包含512×512像素的单通道图像集，图像集中包含圆与方2种形状、3种不同的尺寸、6种不同的纹理并添加了高斯噪声，因此总共包含36种不同的形状、尺寸与纹理的组合。我们通过训练发现其中6种特定的组合，比如带有水平纹理的大方块或者带有垂直纹理的小圆圈等等。我们选择这一类图像分类问题是因为这个问题恰好需要深度伸进网络去解决小尺度与大尺度的问题，比如像素级的纹理和特征级的形状。

为了便于对照，我们部署了本文提出的模型和经典的U-Net［24］模型，我们通过105个随机生成的图像来训练2个模型。2个模型的参数规模与准确率的关系如图4所示。

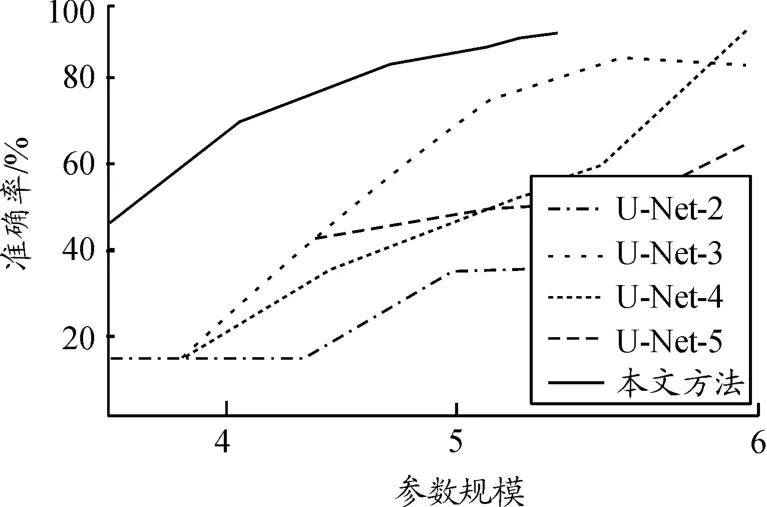
图4 准确率与参数规模的关系

在图4中，用100张图片作为准确率的测试集，本文提出模型的w取值为1，d∈｛25，50，100，200｝；U-Net的规模分别选择为2、3、4、5。在105轮训练内，当全局准确率没有显著变化时，将停止训练。实验结果表明，本文提出模型的初始准确率显著高于U-Net模型，并且随着准确率的提升，本文提出算法的参数规模显著小于对照算法，在任何准确率级别上，参数规模都小于对照算法，并且本文提出算法最终能达到对照算法难以达到的准确率。

为了进一步验证本文提出方法的性能，我们又采用知名的CamVid数据集［25］进行了对照实验，该数据集中包含360×480像素的彩色道路景观图，我们利用其中367张图片作为训练数据，101张图片作为验证数据，233张图片作为测试数据。实验的目标是区分出11类目标，例如汽车、道路、隔离带和人行道等等。我们通过局部对比归一化图像方法训练本文提出模型和U-Net方法，直到全局准确率在验证集上没有显著变化时停止训练。为了增强实验结论的说服力，我们又增加了3种知名算法作为对照方法。实验结果如表1所示。

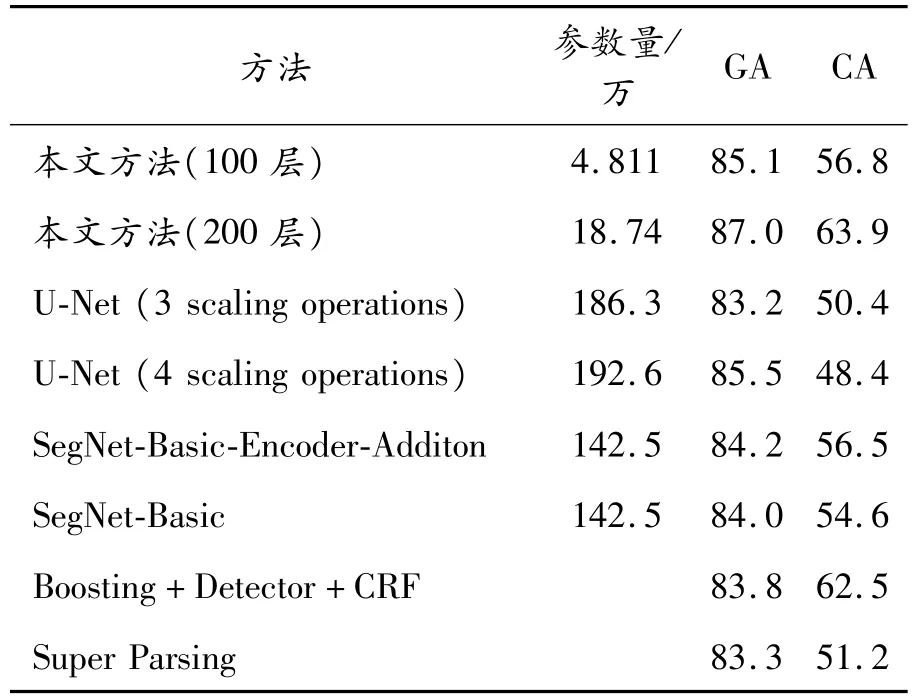
表1 各种算法在CamVid数据集上的性能对比

在表1中，GA代表全局准确率（global accuracy），CA代表类别准确率（class accuracy）。对比算法除了前述的U-Net，还有经典SegNet［16］的2种版本，此外还有Boosting+Detector+CRF和Super Parsing 2类非神经网络方法。如表1所示，本文提出方法在各种对比方法中可以达到最高的全局准确率和类别精度，并且，与神经网络类的算法相比，本文提出算法具有最小的参数规模，从而具有远小于其他神经网络方法的训练和计算开销；与非神经网络类算法相比，本文提出方法的全局准确率明显要高一些。

为了验证本文提出方法具有更好的抗过拟合性，我们将各种对照算法循环训练300轮，测试其在ImageNet数据集中随机挑选的1 000张图片的分类情况，记录其在不同轮数的分类准确率，实验结果如图5所示。

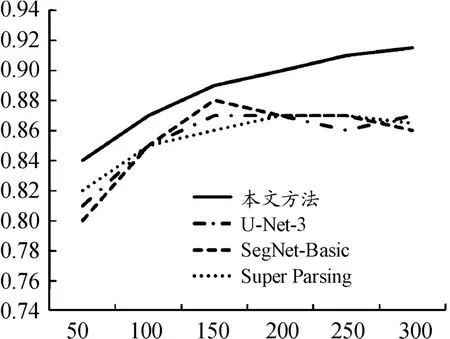
图5 各对照算法再不同训练轮数下的准确率

如图5所示，在300轮训练之内，本文提出方法的分类准确率随着训练轮数的增长而提高，在对照方法中，SegNet-Basic的最高准确率在160轮左右时达到最高，之后陷入过拟合，U-Net（3层）和Super Parsing在训练超过200轮后，准确率产生振荡。实验结果表明，本文提出方法具有更好的抗过拟合性。

为了验证本文提出方法可应用于不同领域，我们在不调整模型参数的情况下，将方法应用于生物细胞数据集的分类上，实验结果如表2所示。

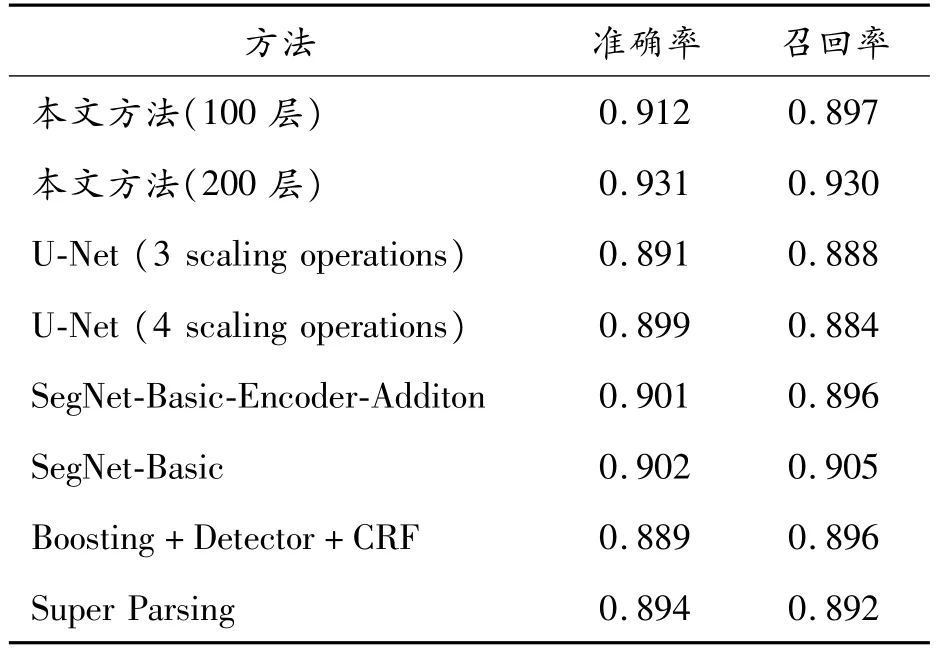
表2 各种算法在生物细胞数据集上的分类性能对比

表2中的数据集是由512×512像素的小鼠淋巴母细胞的断层重建图像组成，图像内的标签包括5类，分别是核膜、常染色质、异染色质、线粒体和脂质滴。如表2所示，在生物细胞图像分类领域，本文提出方法依然能达到最高的准确率和召回率，从而证明了本文提出的模型可自适应地应用于不同领域。

4 结论

本文提出了一种基于规模扩大和密集连接的深度卷积神经网络模型，与传统的深度卷积神经网络采用尺度扩大-缩小的编码-解码方式不同，该模型通过扩大卷积规模可以在同一层使用多个不同规模的特征映射信息，避免了编码-解码的海量参数和巨大的时间开销，并通过密集连接不同层的特征，提高了处理的准确率。实验结果表明，与各种经典神经网络和非神经网络方法相比，本文提出模型具有更简单的参数规模、更高的分类准确率，并且可以自适应地部署于各种类型的图像分类问题，能够避免过拟合，从而达到较高的处理性能。

近年来，深度卷积神经网络在图像处理之外的诸多领域取得成功，例如语音识别和文本处理［26-27］，本文提出模型是否适用于这些领域，在这些领域模型需要做什么样的提升，将是未来有意义的工作。