节点攻击下的海上联合作战网络鲁棒性研究

卢清亮，完颜娟，毛德龙

(1.中国人民解放军92578部队，北京100161；2.军事科学院军事科学信息研究中心，北京100142；3.中国船舶工业系统工程研究院，北京100094)

0 引言

生活中的网络都可以被描述为由节点和边构成的拓扑结构[1–3]，如通信网等基础设施网、身体结构中的神经网络等生物网、虚拟网络中的人际关系网等抽象网络。现实中，网络内部节点与节点的连接变得更加复杂，网络与网络之间的联系也变得越来越紧密。以海上联合作战网络为例，随着装备性能和作战理念的提升，现代海上战争越来越重视多兵力协同作战，在进行反潜作战活动中，可能需协同航母、驱逐舰、护卫舰、反潜飞机、潜艇、海洋监视船、无人航行器等多种兵力，组成跨界面立体反潜防护网络，存在指挥网络和协同探测网络等多种子网络。这些子网络之间是相互联系、相互依赖的，其中任何一个兵力节点出现故障都可能带来一场战争的失败[4]。对于相依网络，当部分节点或边发生故障时，往往会导致其他相互作用的网络节点或者边产生故障，这种失效的风险随着相依程度和网络复杂性的增加而增加[5–6]。因此，开展海上联合作战网络的鲁棒性研究，具有重要的军事意义。

本文依据海上联合作战网络想定，构建双层加权相依网络模型，通过调整负载重分配比例，对比分析作战网络在度正相关、负相关和随机相关3种不同的相依方式下的鲁棒性，可为提高实战背景下海上联合作战网络的鲁棒性提供参考。

1 海上联合作战相依网络模型

以海上联合反潜想定为例，兵力包括1颗海洋监视卫星、1颗通信卫星、1艘驱逐舰、2艘护卫舰、1艘水面无人航行器、1艘海洋监视船、1架反潜直升机、1架反潜巡逻机、2艘潜艇、4艘水下无人航行器、3套水下声基阵，这些兵力之间形成了相互依赖的复杂网络，如图1所示。

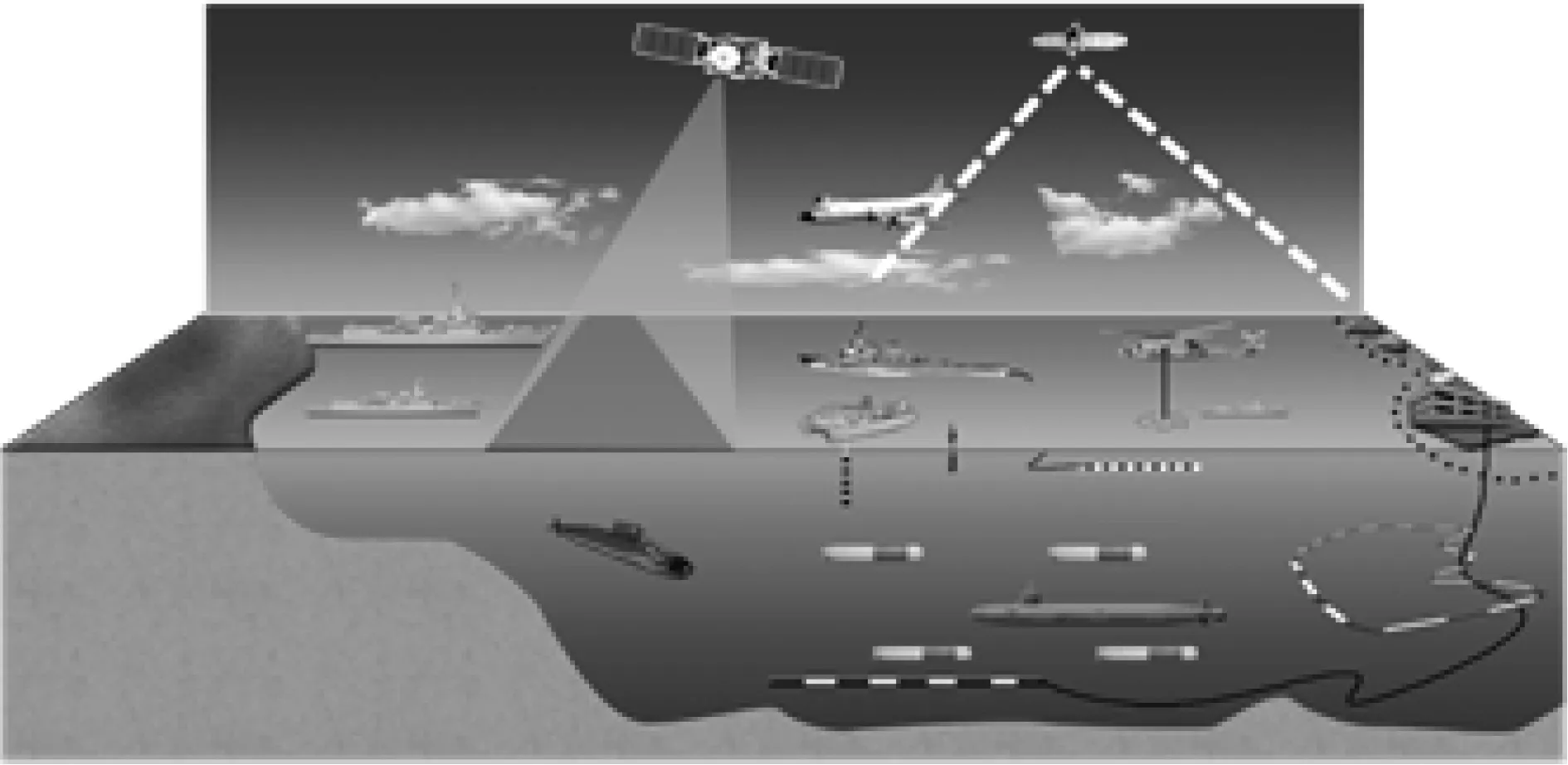
图1 海上联合反潜兵力构成图Fig.1 Navy cooperative anti-submarine force composition

结合复杂网络的理论知识，以水面和水下多兵力协同作战为背景，依据各兵力之间的交互关系，构建出如图2所示的相依网络模型。其中深色节点代表水面和空中兵力，构成子网络A；浅色节点代表水下兵力，构成子网络B。

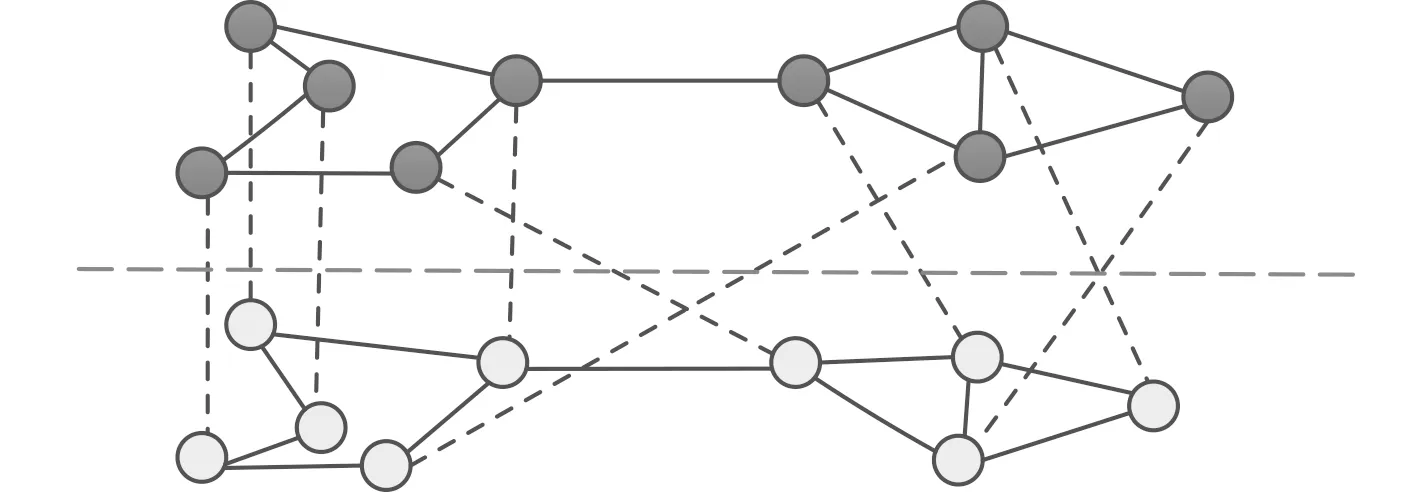
图2 海上联合作战相依网络模型Fig.2 Dependent network model for joint maritime operations

子网络的节点数分别记为NA和NB。设kAi表示A中第i个节点Ai的度，对A网络中各节点的度从小到大进行排序，若kAi=kAj，则2个节点随机进行排序；之后对子网络B中节点排序；将排序后的A网络中Ai节点和B网络中Bj节点进行一对一相依，采用3种不同的相依方式构建相依网络：

1）基于度的正相关相依模式（AL）。选取A网络和B网络中度大的节点，即按照A1↔B1，A2↔B2，···，AN↔BN的方式连接向量A和向量B；

2）基于度的负相关相依模式（DL）。选取A网络中度大的节点和B网络中度小的节点，即按照A1↔BN，A2↔BN-1，···，AN↔B1的方式连接向量A和向量B连接；

3）随机模式（RL）。随机在A网络中和B网络中选取节点对添加互连边，子网络中每个节点只和另一个网络的一个节点建立相依关系。

首先定义节点初始负载为：

其中ρ和τ均是用来控制节点初始负荷的强度的参数。其次定义网络节点容量为：

其中 α≥0lant0 是网络的容许系数，α越大代表一个系统抵御攻击时的能力越强。

α一般会存在一定的阈值，用αc表示，当α>αc时，网络中的任一节点失效不会导致另外的节点失效，当α<αc时，网络中的任一节点失效可能导致其他节点或者整个网络崩溃。

2 基于负载重分配的作战网络级联失效模型

当节点i失效时，节点i传递给其相邻节点j的负载为：

当Lj+∆Lj>Cj时，节点j就会发生失效。该节点失效后同样将其负载向其相邻的未失效的节点按比例传递[7]，如图3所示。

图 3负载重分配示意图Fig.3 Load redistribution diagram

相依网络中负载失效过程如下：

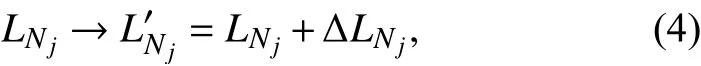
假设完好节点Nj被失效节点分配到的负载比例系数为则

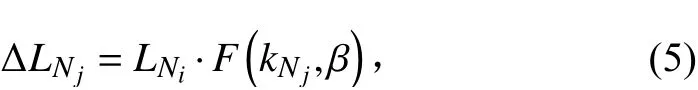
其中，kNj为网络中节点Nj的度，β≥0是负载分配均匀性参数。节点Ni失效后，完好节点Nj在分担其负载时可能与kNj有关，可表示为：其中，c代表权重系数。因此，完好节点j分配到的失效节点i的负载比例可表示为：

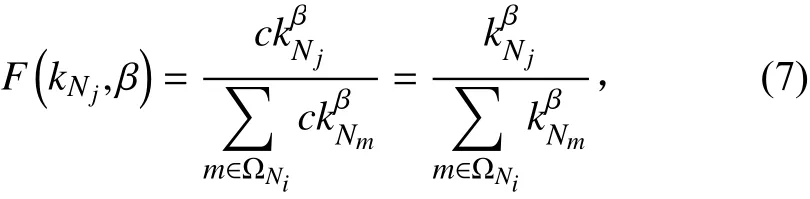
更新节点Nj负载为：

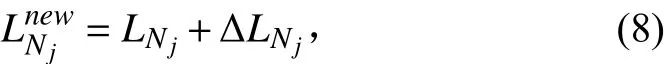
对所有Nj判断下式是否成立：

若成立，则该节点失效，并运行至不再产生新的失效节点。

3 仿真实验

作战系统具有小世界和无标度网络特征[8]，构建节点数为200、平均度为4的2个BA无标度子网络，再分别采用随机、度正相关、度负相关3种不同的相依方式将这2个子网络构建为相依网络。

1）在一定的容许系数和初始负载强度参数的情况下，分析不同负荷分配均匀性参数时随机相依网络发生级联故障后剩余节点的比例，仿真结果如图4所示。图中垂直竖线表示均匀性参数β与初始负载强度参数τ相等时剩余网络规模的情况。

当τ=0.7时，在β=τ时剩余节点比例比较高；当τ=1时也可以得到相同的结论。但是当τ=1.4和1.7时，在一定的容忍参数下，随着β的增大，网络剩余节点的比例有增高的趋势，即β>τ时网络抵抗级联毁伤的能力更强。这表示随机相依网络A网络中部分度小的节点可能与B网络中度大的节点相连，若A网络中度小的节点失效，故障更容易传递到相依的B网络中。因此，提高负载分配非均匀性参数可有效提高海上联合作战网络的鲁棒性。

2）在一定的容许系数和初始负载强度参数情况下，分析不同的分配均匀性参数时度正相关相依网络发生级联故障后剩余节点的比例，仿真结果如图5所示。

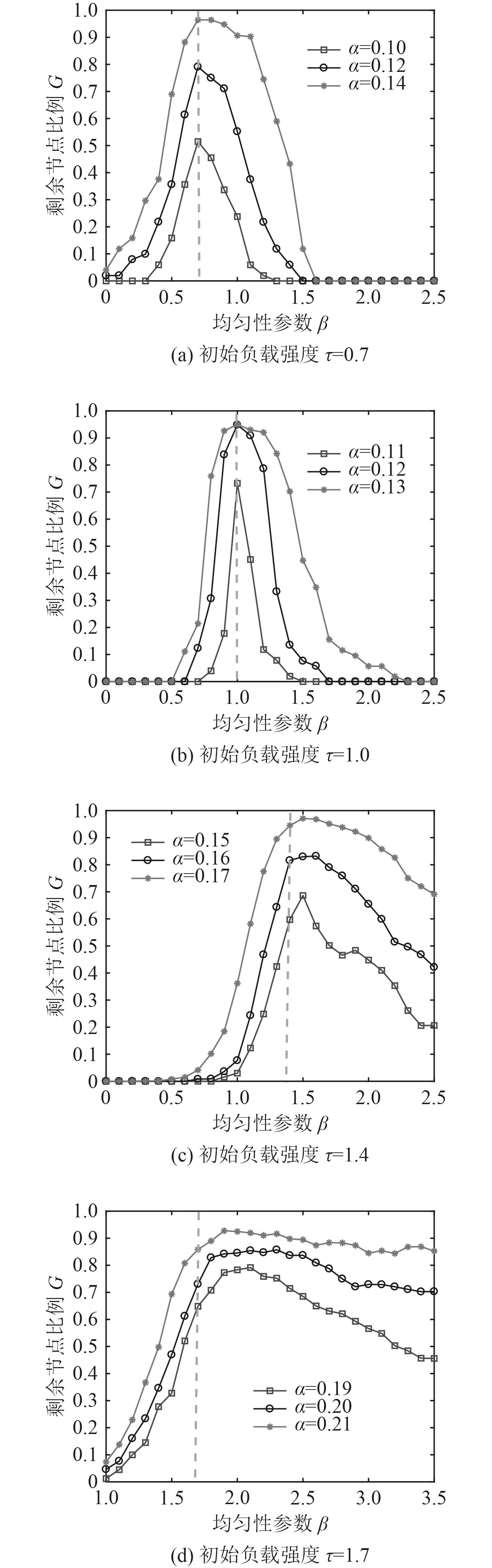
图4 随机相关模式下分配均匀性参数与剩余网络规模G的关系Fig.4 Relation between distribution uniform ity parametersand residual network sizeunder random correlation model

由图5可以发现，无论τ=0.7，1，1.4或1.7，β=τ附近的网络剩余节点比例都比较都高，网络的鲁棒性都较强。这表示相依网络A网络中度大的节点和B网络中度大的节点相连，相依不会对2个网络阈值产生影响。因此，对于度的正相关相依网络，初始负载强度和负载均匀性参数相同时，网络抵抗级联失效的能力较强。

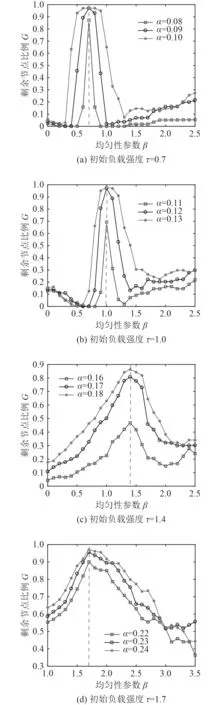
图5 正相关模式下分配均匀性参数与剩余网络规模G关系Fig.5 Relation between distribution uniformity parametersand residual network sizeunder positive correlation mode

3）在一定的容忍参数和初始负载强度参数情况下，分析不同的分配均匀性参数时度负相关相依网络发生级联故障后剩余节点的比例，如图6所示。

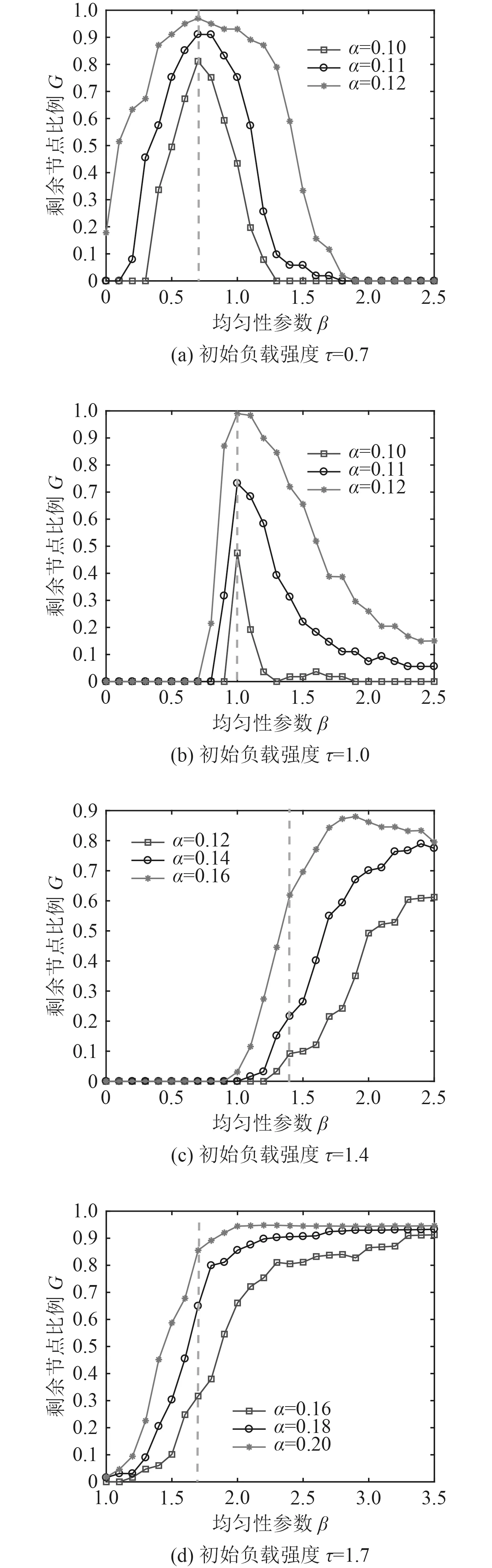
图6 负相关模式下分配均匀性参数与剩余网络规模G关系Fig.6 Relation between distribution uniformity parametersand residual network size under negative correlation mode

由图6可以发现，无论τ=0.7或1，β=τ附近的网络剩余节点比例都比较高，网络的失效比例都较少，当权重系数和分配均匀性系数相近时，对网络有一定的保护作用。但是当τ=1.4，1.7时，可以明显看出β>τ，随着β增大，相同容量参数下网络的最大剩余图G值越大，网络抵抗级联失效的能力也就越强。这表示在度的负相关相依网络中，由于度大的节点和度小的节点之间存在相互依存的关系，保护一个子网络中度小的节点，便会保护另一个相互依存网络中度大的节点，降低网间失效程度。因此，可以通过适当提高网络分配均匀性参数，提高网络抵抗级联失效的能力。

4 结语

本文研究兵力节点遭到攻击失效时，负载重分配比例和相依模式对海上联合作战网络鲁棒性的影响。从仿真结果可以看出，对度正相关的作战网络，按初始比例分配任务和信息量能保证其鲁棒性最强；对于度随机相关或负相关的作战网络，需通过适当调整分配的非均匀比例来提高网络的鲁棒性。本文研究方法及研究结果可为提高某一具体海上联合作战网络的鲁棒性、制定联合作战计划提供支撑。