基于注意力机制融合多阶邻域信息的网络表示学习模型
陈 斌,李金龙
(中国科学技术大学 计算机科学与技术学院,合肥 230027)
1 引 言
网络表示学习(Network Representation Learning,NRL),也称为图嵌入(Graph Embedding,GE),旨在将图中节点表示成低维稠密实值向量,然后作为节点的特征被应用于实际应用任务,如节点分类[1]、链接预测[2]以及图分类[3]等.为了获得更好的网络表示并且在实际应用任务中获得更好的表现,需要充分利用图的拓扑结构、节点特征和边的特征(如果可用)中蕴含的丰富信息.
由于卷积神经网络(Convolutional Neural Network)具有提取局部空间特征的能力,近年来已经在各种具有挑战性的任务中被证明是有前景的,特别是在计算机视觉(Computer Vision,CV)和自然语言处理(Natural Language Processing,NLP)领域.其底层处理的数据,如图像和文本等都可以表示为特殊形式的图,都具有规则的网格结构.然而不能将CNN直接应用于一般形式的图数据,由于存在以下两个问题:1)图数据中每个节点的邻居大小不一;2)节点的邻居节点没有固定的顺序.
将CNN推广应用到图数据上的工作可以分为两大类,分别为基于频谱(spectral-based)的方法,和基于空间(spatial-based)的方法.基于频谱的方法从图信号处理的角度引入滤波器来定义图卷积,其中图卷积运算被解释为从图信号中去除噪声,不同方法[4-6]间关键的区别在于滤波器的选择不同.基于空间的方法则是通过信息传播来定义图卷积,相比于基于频谱的方法具有更好的扩展性.
Kipf等人提出的图卷积网络(Graph Convolutional Network,GCN)[7]填补了基于光谱方法和基于空间方法之间的差距,是基于频谱的图卷积的一阶近似,同时采用邻域聚合方案,将节点特征与相邻节点的特征迭代聚合为节点新的特征.
消息传递神经网络(Message Passing Neural Network,MPNN)[8]概述了基于空间的卷积神经网络的一般框架.它把图卷积看作一个消息传递过程,在这个过程中信息可以沿着边直接从一个节点传递到另一个节点.为了让信息传递得更远,可以迭代执行K步消息传递过程.由于节点的邻居数量不一致,可能是1个,也可能是1000个甚至更多,GraphSAGE[9]对每个节点进行采样,以得到固定数量的邻居,降低了计算时间复杂度.图注意力网络(Graph Attention Network,GAT)[10]在进行邻域聚合时,采用注意力机制为不同的邻居节点分配不同的权重系数,提升了节点分类的性能.
这些方法在一个图卷积过程中只考虑了节点的1阶邻居节点,而忽视了节点的高阶邻域信息.因此在实际使用时通过堆叠多个图卷积层来提升模型性能.GCN在使用两个图卷积层时获得了最佳节点分类性能.然而,当模型变得更深,获取的信息更多时模型反而表现得更差.GCN模型实际上是Laplacian平滑[11]的一种特殊形式,模型越深会引起过度平滑,导致节点无法区分.实际上,图卷积层数的选择仍然是一个有待解决的问题.
由于输入图的结构信息是多种多样的,因此没有统一的规则来确定图卷积层的数量,一种替代方案是在一层中混合不同阶邻居节点的信息.JK-Net[12]将网络的最后一层与之前的隐层连接起来,然后有选择地利用不同隐层提取的局部信息.MixHop[13]提出新的图卷积层,使用可训练聚合参数将不同阶邻居节点的信息进行混合.
在本文中,我们提出了一种新的网络表示学习模型,即多邻域注意力图卷积网络(MAGCN),综合考虑了节点的属性信息、图的局部(1阶邻域)和全局(高阶邻域)结构信息.本文的创新点有以下3点:1)基于注意力机制,使用邻接矩阵的幂作为屏蔽矩阵,生成多个融合各阶邻域信息的节点表示;2)为了能够获得包含更多信息的节点表示,通过改进的动态路由算法将不同的节点表示自适应地聚合成一个;3)我们在Cora、Citeseer 和Pubmed 3个引文网络数据集上进行了节点分类实验,相比其他方法具有更高的分类准确率.
2 多邻域注意力图卷积网络
图1描述了MAGCN模型结构,主要包含两个部分,即多注意力图卷积层和隐状态聚合层.多注意力图卷积层将邻接矩阵的幂作为屏蔽矩阵,从各阶邻域提取子结构特征,获得节点的多个中间表示,我们称之为隐状态.隐状态聚合层用于自适应地将局部结构特征聚合在一起作为最终的节点表示.接下来我们将分别介绍这两个组成部分.

图1 MAGCN结构图Fig.1 Architecture of MAGCN
2.1 多注意力图卷积层
图2展示了多注意力图卷积层的工作流程.该层的输入为图的邻接矩阵A和节点的特征矩阵X,A∈N×N,X∈N×F,N是节点个数,F是节点特征的维度.输出是新的节点特征矩阵集合,即节点中间表示,我们称之为节点的隐状态.输出的节点中间表示的个数和使用的邻接矩阵幂的个数一致,即,如果我们使用了邻接矩阵的1次,2次,…,K次幂,则输出为H1,H2,…,HK.

图2 多注意力图卷积层流程图Fig.2 Workflow of multi-attention graph convolution layer
首先,我们应用线性函数将节点特征矩阵X转换成高级别特征X′,线性函数如公式(1)所示:
X′=[X1′,X2′,…,XN′ ]=XWt
(1)
其中,Wt∈F×F′是一个可训练权重矩阵,F′是第i个节点的高级别特征.Xi′和Xj′之间的注意力系数eij将由兼容性函数a(Xi′,Xj′)计算得到,如公式(2)所示:
(2)
其中wu,wv∈F′是可训练参数,LeakyReLU是非线性激活函数.注意力系数eij衡量了Xi′和Xj′之间成对的依赖关系.接下来,我们基于节点之间的连边关系调整注意系数eij,如公式(3)所示:
(3)
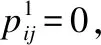
为了使不同节点之间的注意力系数易于比较,使用softmax函数对所有注意力系数进行归一化,如公式(4)所示:
(4)
(5)
其中,σ(·)是非线性激活函数.
我们将公式(3)中的A替换为邻接矩阵的2次,3次,…,K次幂,从而得到第i个节点与它的高阶邻居之间的注意力系数,这样我们就可以为每个节点生成多个输出特征矩阵.这个过程可以用公式(6)来概括.
(6)
其中,k∈{2,…,K},Bk是指将邻接矩阵的k次幂中大于0的值置为1得到的矩阵;Nik是图中第i个节点的k阶邻居节点集合,Hik∈F′是第i个节点的第k个隐状态,σ(·)是非线性激活函数.
2.2 隐状态聚合层
多注意力图卷积层输出了一组节点隐状态[H1,…,HK],每一个都捕获了k阶邻居的局部结构信息,k∈{1,…,K}.为了自适应地将这些隐状态聚合到节点的最终表示形式,我们提出了隐状态聚合层.

(7)
(8)
其中,Wk∈F′×F′是一个权重矩阵;ck是耦合系数,是bk(从子胶囊到父胶囊的对数先验概率)在softmax函数处理下的结果,如公式(9)所示:
(9)
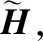
(10)
(11)
其中,⊙是元素级(element-wise)乘法,Hi′表示H′的第i行,∑表示对所有矩阵元素求和.
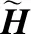
2.3 模型训练
为了训练我们的模型,我们使用节点分类任务构建目标函数.在隐状态聚合层之后,我们得到了节点的最终特征表示矩阵H∈N×F′,然后我们将其输入到图卷积层(由公式(12)定义)用于预测未标记节点的标签.
(12)

我们的模型是通过最小化所有带标签节点的交叉熵损失来训练的,如公式(13)所示:
(13)
其中,yl是带标签节点的下标集合,Hlcnode指的是第l个带标签节点的图卷积层输出的第c项.Ylc表示第l个带标签节点的真实值.
3 实验结果与分析
3.1 实验数据集
为了验证我们提出的模型(MAGCN)的性能,我们在节点分类任务上与之前的先进模型进行了比较.我们使用了3个基准数据集:Cora,Citeseer和Pubmed[15];这些数据集是引文网络,其中节点表示文档,边表示文档之间的引用,标签表示的是文档所属的类别.每个节点的特征由词袋(bag-of-word)表示,特征的维度由语料库大小决定.对于每个数据集,每种标签下有20个节点用于训练.此外,有500个节点用于验证,1000个节点用于测试.有关这些数据集的详细统计信息,见表1.
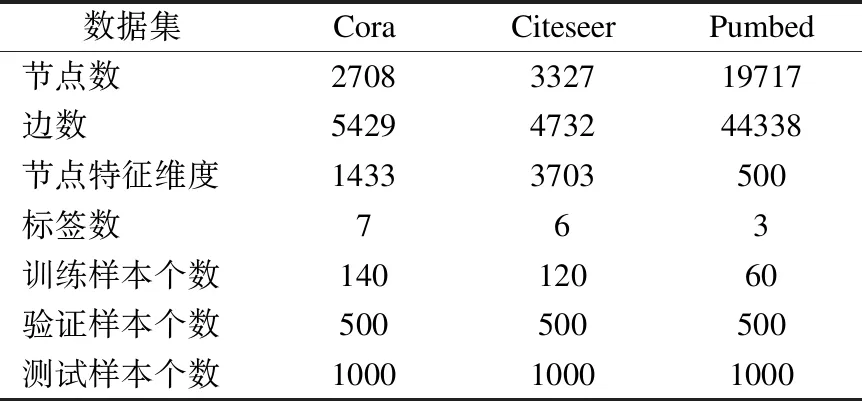
表1 节点分类实验数据集描述Table 1 Details of datasets for node classification
3.2 实验设置
对于节点分类,在多注意力图卷积层中,我们使用了多头注意力机制,即独立运行图卷积多次,然后将所有图卷积后的输出拼接在一起.对于Cora和Citeseer数据集,多注意力图卷积层由8个注意力头组成,每个注意力头输出8维特征表示;对于Pubmed数据集,多注意力图卷积层由4个注意力头组成,每个注意力头输出4维特征表示.此外,所有数据集上的邻居阶数最大值均取值为3.
我们使用Adam[16]随机梯度下降优化器对我们的模型进行训练,以最小化训练节点上的交叉熵,最多训练3000次,即3000个epochs.Cora、Citeseer和Pubmed数据集的学习率分别设置为0.005、0.0085和0.005,L2正则化的权重分别设置为0.01、0.002和0.005.动态路由迭代次数r设置为3次.我们通过提前停止策略(early stopping strategy)来终止训练,即验证集节点上的交叉熵损失在100个连续的epoch都不下降时结束训练.此外,为了避免过拟合,我们在模型各层之间都使用了Dropout[17],其比率设置为0.5.对于所有数据集,我们运行模型10次,并使用平均分类精度和标准偏差作为最终结果.所有训练都使用Pytorch-1.2.0,以及Fey等人提供的几何深度学习扩展库Pytorch Geometric[18],并在单块Nvidia GTX-1080Ti GPU卡上完成.
3.3 节点分类
3.3.1 模型对比
我们将我们的模型与DeepWalk[19]、Planetoid[15]、Chebyshev[6]、GCN[7]和GAT[10]进行了比较,这些模型在节点分类精度方面都是目前最先进的模型.Cora、Citeseer和Pubmed数据集上的节点分类精度结果汇总见表2.
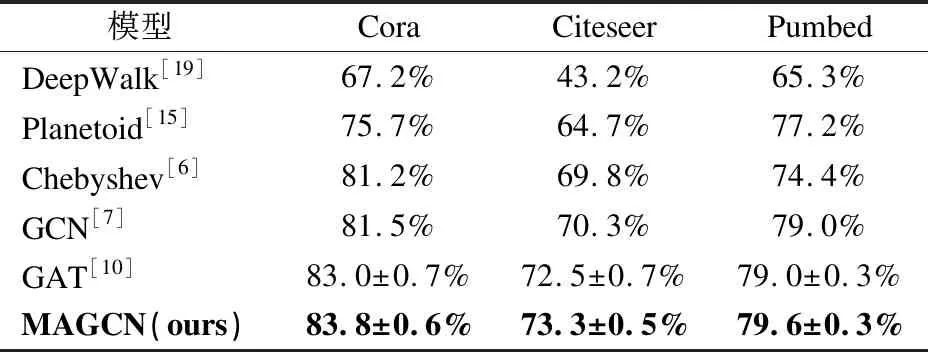
表2 节点分类任务分类正确率Table 2 Test accuracy on node classification
对比方法的所有结果均来自其原始文献.结果表明,我们的模型在所有数据集上始终保持最佳性能,这意味着MAGCN确实能够通过探索高阶邻域信息来学习更多的鉴别节点的特征.与GAT直接比较,我们的MAGCN在所有3个数据集上的性能分别提高了0.8%、0.8%和0.6%.注意,与同样使用注意力机制的GAT相比,我们的MAGCN在学习节点表示时仅多考虑了高阶邻居的信息.此外,我们还观察到,与GAT相比,MAGCN在3个数据集上的分类准确率标准偏差更小,这说明MAGCN的训练更稳定.
3.3.2 参数分析
在GCN中,叠加多个图卷积层(K层)可以增加一个节点的接受域,使其能覆盖到它的K阶邻居.在我们的MAGCN中,节点的接受域由邻居阶数的最大值(即K值)参数控制.为了研究邻居阶数的最大值与节点分类性能之间的关系,我们在节点分类任务中使用了不同的K值.结果汇总在表3中,结果表明,随着邻居阶数的最大值增加到3,模型节点分类的性能将会逐步得到改善.但是当邻居阶数的最大值超过3时,即在学习节点表示时,考虑了节点的3阶以上邻居,使得MAGCN可能会从不太相关的邻居那里获取大量信息,从而无法学习合适的节点表示.此外,对于节点分类,GAT模型包含两层,这意味着节点的接受域是它的2阶邻居.通过将邻居阶数最大值的参数设置为2,我们的MAGCN具有与GAT相同的模型容量,但实验结果显示我们的模型具有更好的表现,如表3中K值取2的行所示.

表3 不同K值在节点分类准确率方面的比较Table 3 Comparison of difference K interm of node classification accuracy
在GAT中使用多头注意力旨在用来增加模型的容量,但并没有给出具体的解释.为了探寻使用多头注意力机制对提升模型性能是否有效,我们进行了相关实验.通过设置多注意力图卷积层中的相关参数,即使用不同数量的注意力头,每个注意力头输出不同维度的特征表示,其他设置保持不变,在Cora数据集上的实验结果如表4所示.注意,为了使得多注意力图卷积层之后得到的节点表示维度一致,注意力头数量乘上每个注意力头输出表示的维度需保持一致.

表4 不同数量注意力头的实验结果Table 4 Experimental results of different #heads
从表4的结果来看使用8个注意力头在Cora数据集上的节点分类准确率最高,而使用4个注意力头时标准差更小,训练更稳定.对比只使用单个注意力头,多头注意力机制确实能提升模型的性能.
3.3.3 隐状态聚合层的删减实验
设计隐状态聚合层的目的是为了能自适应地聚合从不同阶邻居学习到的节点的隐状态.为了验证它是否有效,我们进行了如下实验:用简单的add操作替换隐状态聚合层.具体来说,在我们得到节点的隐状态(H1,H2,H3)之后,直接通过H=H1+H2+H3来计算节点的最终表示.其它部分则保持不变.有/无隐状态聚合层的MAGCN之间的比较结果汇总在表5中,其中MAGCNO表示用add操作代替隐状态聚合层的MAGCN.结果表明,在Cora、Citeseer和Pubmed数据集上,使用隐状态聚合层可以提高模型的性能,准确率分别提高了1.2%、1.0%和0.6%.这些结果表明,隐状态聚合层能够合适地确定不同阶邻居信息对最终节点表示的贡献,从而使得最终学到的节点表示更完善.

表5 有/无隐状态聚合层的MAGCN实验结果Table 5 Experimental results of MAGCN with/without hidden state aggregation layer
3.4 可视化
对网络表示学习效果的另一种评估方式是对学习到的网络表示进行可视化.Cora数据集的节点共有7种不同的类别标签,很适合进行可视化.我们首先使用MAGCN与node2vec[20]模型以及GCN模型学习节点的低维向量表示,然后将学习到的节点向量表示输入到t-SNE[21]模型中.t-SNE会将节点表示映射到二维向量空间中的一个点,即每一个节点在二维空间中有一个坐标,以实现可视化.每一种类别标签对应一种形状,具有相同类别标签的节点在二维空间中对应的点具有相同的形状.
图3展示了不同模型学习到的节点表示的可视化效果.从可视化结果来看,我们的MAGCN可视化效果最好,能观察到明显不同的7个簇,而且簇与簇之间的间隔也相对比较大.由于node2vec只利用了原始网络的结构信息,忽略了节点的属性信息,导致学习到的节点表示在可视化时未能形成明显的簇,具有不同标签的节点混合在一起的情况比较严重,还有数个节点远离了中心.GCN模型的可视化效果较node2vec有了很大的提升,具有相同标签的节点大致分到了一起,但是簇与簇之间的边界还是不够明显.由于GCN和MAGCN都考虑了节点的属性信息和结构信息,因此可视化效果较node2vec更好,此外,由于我们的MAGCN考虑了节点的多阶邻域信息,而且使用了注意力机制,使得我们的模型具有更好的可视化表现.
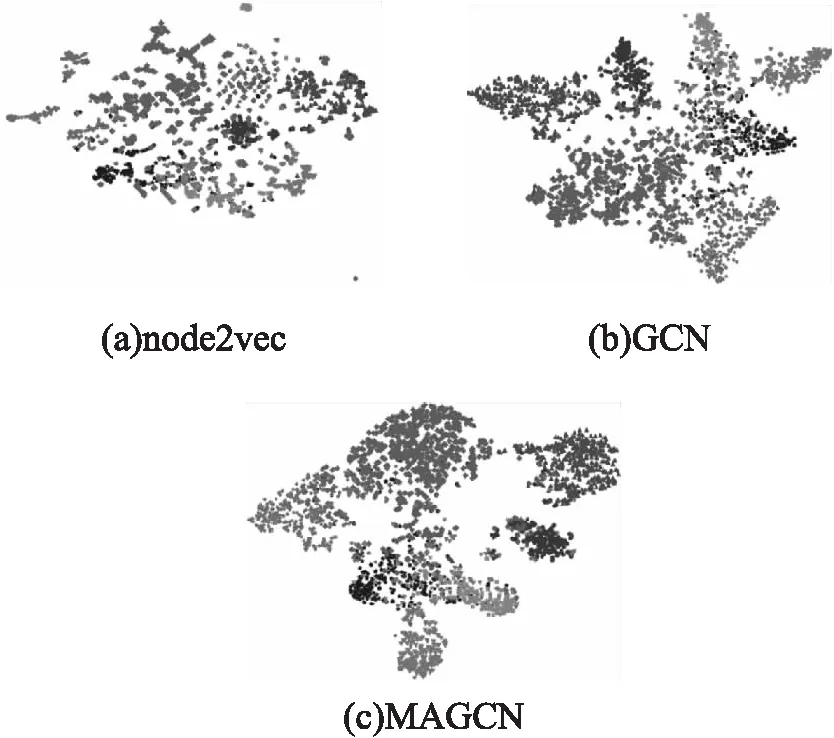
图3 Cora数据集t-SNE可视化Fig.3 t-SNE visualization on Cora dataset
4 结论与展望
在本文中,我们提出了基于注意力机制的融合多阶邻域信息的网络表示学习模型MAGCN,以利用图中蕴含的丰富信息学习节点表示.设计了多注意力图卷积层,用于捕获图的局部和全局结构信息,生成不同的节点表示;隐状态聚合层采用动态路由算法,将不同节点表示聚合在一起,生成最终的节点表示.在3个引文网络上的节点分类任务的实验结果表明,该模型与现有方法相比具有更高的分类准确率.此外,我们的模型具有更好的可视化效果.接下来的工作可考虑寻找一种新的结构,能够根据输入图数据的特征自适应确定使用多少阶邻居信息更合适,并在更多的任务中评估MAGCN的性能.

