考虑涡泄模式的低质量比圆柱涡激运动数值模拟

孙洪源，何栋梁，林海花，常 爽，于福临

(1. 山东交通学院 船舶与轮机工程学院，山东 威海 264209；2. 中国海洋大学 工程学院，山东 青岛 266100)

0 引 言

随着海洋浮式结构的广泛应用，Spar 海洋平台、Spar 型浮式风电基础等所包含的立柱式结构，在一定流速下发生涡激振动的现象。为了区别，将这种长径比比较低、漂浮于水面的刚性结构物的涡激振动现象称为涡激运动。涡激运动涉及诸多科目，如流体力学、计算流体力学、振动学、结构力学和统计学等[1]。

海洋结构物涡激运动（Vortex induced motion，VIM）这一热点问题越来越受到深海工程技术人员和研究人员的关注，它是典型钝体绕流中升力和拖曳力所导致的直接后果[2]。目前国际上已有一些学者对涡激运动进行了研究，其中包含对海洋平台等结构物进行涡激运动集体预报等[3-5]。深水Spar 平 台、浮筒等均具有特殊的深吃水立柱式结构，当水流经过时，圆柱体后方发生周期性涡旋分离，致使结构受到沿流向的拖曳力以及垂直于流向的升力[6]。

本文重点研究的是低质量比圆柱与浮式圆柱涡激运动特性之间的关系。将运动系统简化为质量（m）-弹簧（k）-阻尼（ζ）系统，分析浮式圆柱运动的控制方程并通过4 阶Runge-Kutta 法离散，得到一段时间内步长的速度和位移。通过软件的自定义功能编程并嵌入到Fluent 软件中，可以实现圆柱体的运动以及流场的更新，流场更新后再次反作用于圆柱，实现圆柱与流体的流固耦合。这已成为安全性及运动性能评估方面必须考虑的重要原因[7]。

1 数值计算模型

1.1 涡激运动的主要研究方法

随着计算机技术的发展，计算流体力学（CFD）方法逐渐应用到研究浮式海洋平台涡激振动的问题中[8]，采用数值模拟方法弥补了模型试验对于一些多参数的敏感性分析和流场捕捉方面成本太高的不足。为了保证有限元仿真的可靠性，在建模时需要考虑模型的力学性质，采用合理的单元类型和应变方程去模拟实际的结构[9]。

涡激运动的研究在于规定流体的参数，因为它与许多参数有关，这些参数都会直接或者间接影响这个流体力。

1.2 涡激运动的相关参数

1）雷诺数：Re=Uc·(D/v)；

2）斯托哈尔数：S t=fv·(D/Uc)；

3）约化速度：Ur=Uc·(TSWAY/D)；

4）无量纲振幅：A/D(=[Amax−)Amin]/2D；

5）质量比：m∗=m/πρD2L/4。

式中：Uc为水来流速度；D为圆柱动力直径；V为水粘性系数；L为圆柱高度；fv为圆柱涡泄模式频率；TS WAY为圆柱横摇周期；A为 圆柱运动幅值；ρ为流体密度。

1.3 涡激运动求解过程

本文将弹性支撑圆柱的涡激运动系统简化为质量-弹簧-阻尼系统，如图1 所示。

图1 弹性支撑圆柱涡激运动模型Fig. 1 Vortex-induced motions model of elastically supported cylinder

均匀流中，圆柱涡激运动控制方程为：

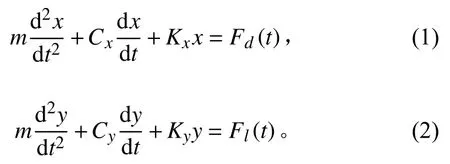
式中：t为 时间；m为质量；Cx=4πmζx fnx和Cy=4πmζy fny分别为顺流向和横流向运动的阻尼系数，其中 ζ为阻尼比；Kx和Ky分别为顺流向和横流向的系统刚度；x和y分别为顺流向和横流向涡激运动位移；Fd(t)为阻力；Fl(t)为升力。

本文计算区域与流场网格划分情况采用圆柱直径D=0.1m，计算区域大小为 20D×4 0D，速度入口距离圆心位置为10D，压力出口距离圆心位置为 30D，上下边界为滑移型距离圆心1 0D，柱体表面边界为无滑移型。为了考虑涡激运动数值模拟的动网格应用，圆柱周围设置了直径 7D的随体网格，随体网格采用结构网格，其他区域采用非结构网格。流场计算应用Fluent 求解器，选择SSTK−ω湍流模型，近壁面中设置了10 层边界层，边界层高度为0.14，网格高度符合y+≈1（y+是无量纲化的壁面距离）。动量方程中的压力-速度耦合应用SIMPLEC 算法。为了减少数值的耗散，动量、湍流动能、耗散率应用2 阶迎风格式。

网格划分既要保证足够的计算精确程度，又要兼顾运算的时间成本。在正式计算之前需要测试网格的密度，以获得最佳效果。由于在数值模拟中采用了动网格技术，所以单纯的测试圆柱绕流并不能获得计算精度与时间的最优方案。本文在质量比m∗=2.6，两向固有频率相等fnx=fny=0.38 Hz 的条件下，测试了在约化速度Ur=5 的圆柱涡激运动，结果见表1。考虑计算精度与时间成本，本文选择了网格b 作为最优方案。

表1 网格测试结果Tab. 1 Grid test results

2 实验结果与分析

2.1 计算工况

为了验证数值模拟方法的可靠性，选择质量比为2.6 的工况与Jauvtis 和Williamson[10]实验结果进行对比。后期对质量比2.6 的圆柱与质量比为1 的浮式圆柱进行涡激运动特性研究比较，具体工况信息如表2 所示。

表2 计算工况表Tab. 2 Calculation condition table

2.2 涡泄模式的比较

图2 为不同响应分支所对应的涡旋泄放模式：左侧方为数值模拟结果，右侧方为Jauvtis 和Williamson的实验结果。

在初始涡旋泄放模式有2 种，分别为S S模式和2S模式。在初始分支的开始阶段，由于顺流向幅值大于横流向幅值处于主导地位，涡泄模式表现为特有的S S（streamwise symmetric vortices shed per cycle）模式，即每个周期泄放一对对称的涡旋，如图2（a）所示。随着流速增加，横流向振幅一旦大于顺流向振幅时，涡旋泄放即表现为 2S（two single vortices shed percycle）模式，如图2（b）所示。

在上端分支，当横向振幅达到最大值时，旋涡泄放出现了 2T（two triplets of vortices per cycle）模式，如图2（c）所示。

在下端分支，涡旋泄放表示为 2P（two pair vortices shed per cycle）模式，即1 个周期泄放2 个涡，如图2（d）所示。

图3 给出了 2T模式在1 个周期的旋涡图，当圆柱处于横流向最大位移时，速度最小但加速度最大，在这种较大加速度作用下产生了3 个涡。其中一个涡的旋转方向与另外2 个相反，且这个涡的强度小于其余2 个，数值计算较好模拟了这一特有现象。

图2 不同响应分支对应的涡泄模式Fig. 2 Vortex release modes corresponding to different response branches

图3 2T 涡泄模式1 个周期内的涡旋图Fig. 3 2T Vortex diagram within one cycle of vortex release mode

2.3 幅值比较

图4给出了不同约化速度下无量纲振幅与实验结果的对比。由图4（a）可见，数值模拟与实验所得的无量纲横流向振幅Ay∗曲线变化趋势是一致的，同样表现出：初始分支I（Initial branch）、上端分支U（Upper branch）、下端分支L（Lower baranch）以及去同步化阶段D（Desynchronization）。特别在初始分支、下端分支和去同步化阶段，数值模拟与实验结果吻合良好，能够真实反映实验结论。然而在上端分支，数值模拟没有达到实验中的最大横流向振幅。同样对于图4（b），数值模拟与实验所得的无量纲顺流向振幅Ax∗曲线趋势大致吻合，只是在上端分支的顺流向振幅有所低估。出现这种现象是因为在上端分支时，圆柱的运动幅值相对较大，大大减弱了圆柱的轴向相关性，而在二维圆柱数值模拟中，内部假设了其轴向是完全相关的[11]。另外，Fluent 数值模拟中采用了雷诺平均法，未考虑流场中的随机扰动[12]。通过比较可以得出结论：应用数值计算可以较好的模拟圆柱涡激运动，但在最大振幅峰值方面有所低估。

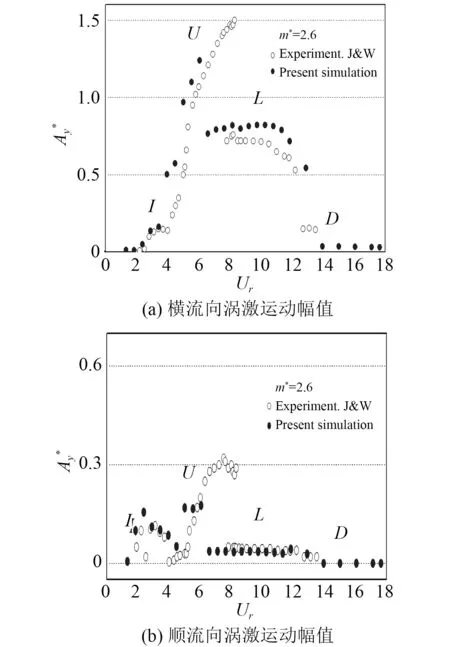
图4 不同约化速度下无量纲振幅与实验结果的对比Fig. 4 Comparison of dimensionless amplitude and experimental results at different reduction speeds

2.4 轨迹比较

图5给出了不同约化速度下，数值模拟与Jauvtis和Williamson 实验所得的运动轨迹比较。数值模拟所得到的初始分支、上端分支和下端分支的圆柱运动轨迹与实验结果基本相似，再次验证了数值模拟方法的可靠。

2.5 考虑涡泄模式的浮式圆柱涡激运动特性

随着约化速度的不断增加，顺流向涡激运动频率均为横流向涡激运动频率的2 倍关系。Ur=4.47 处于涡激运动初始分支的后部，对比图2（b），同样在低阻尼比条件下，质量比2.6 的圆柱表现为 2S模式，而质量比为1 的浮式圆柱表现为 2P模式。图6 给出了此约化速度下一个周期的涡旋泄放图。

Ur=7.11 处于涡激运动的上端分支，与图2（c）一样表现出 2T模式。顺流向涡激运动频率为横流向涡激运动频率的2 倍关系。

图5 不同约化速度下圆柱运动轨迹Fig. 5 Cylindrical trajectory under different reduced speeds

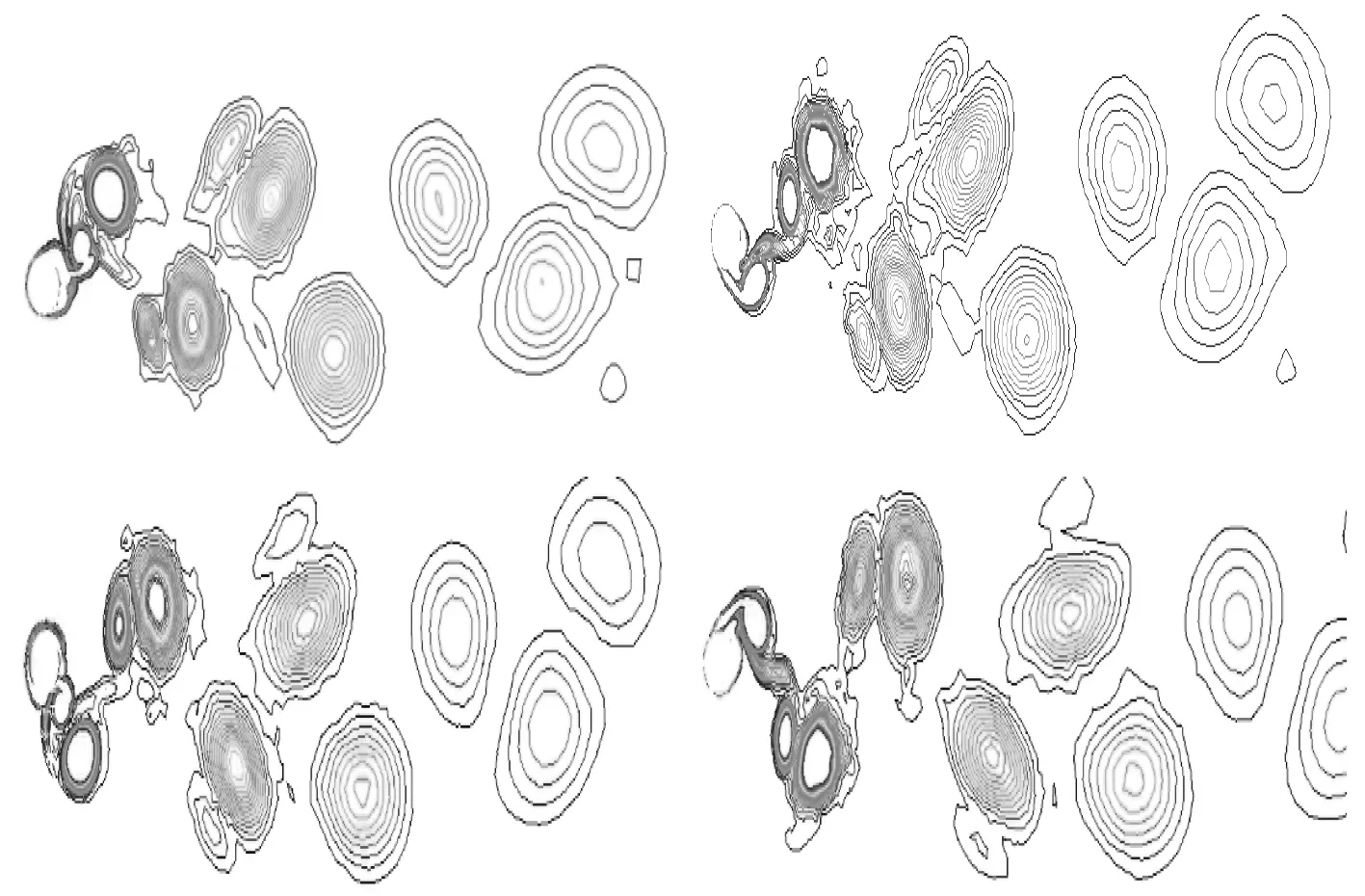
图6 浮式圆柱涡激运动在 Ur =4.47 时一个周期涡泄图（m*=1，）Fig. 6 A periodic vortex release diagram of floating cylindrical vortex induced motion at Ur=4.47（m*=1，）

Ur=11.84 处于涡激运动的下端分支，涡泄模式与图2（d）一样表现为 2P模式。Ur=20.26 处于下端分支与去同步化分支过渡区域，横流向涡激运动频率有2 个，分别是0.66 Hz 和1.61 Hz，0.66 Hz 与下端分支中的锁定频率相近，1.61 Hz 与该流速下的固定圆柱绕流频率相等。虽然横流向运动表现为2 个频率，但由于在去同步化分支中涡激运动幅值非常小，涡泄模式表现为2S模式。

表3 给出了质量比为1 的浮式圆柱横流向、顺流向涡激运动响应谱，图7 给出了各自对应的涡泄图。顺流向与横流向频率比为2 倍关系，初始分支和去同步化分支涡泄模式为 2S模式，其他响应分支为 2P模式。

可以看出它的上端分支的范围很小，与初始分支难以区分，所以上端分支中的 2P涡泄模式表现并不明显。与图2 对比可见，同样在低质量比条件下，浮式圆柱的涡旋泄放表现出了不同的形式。

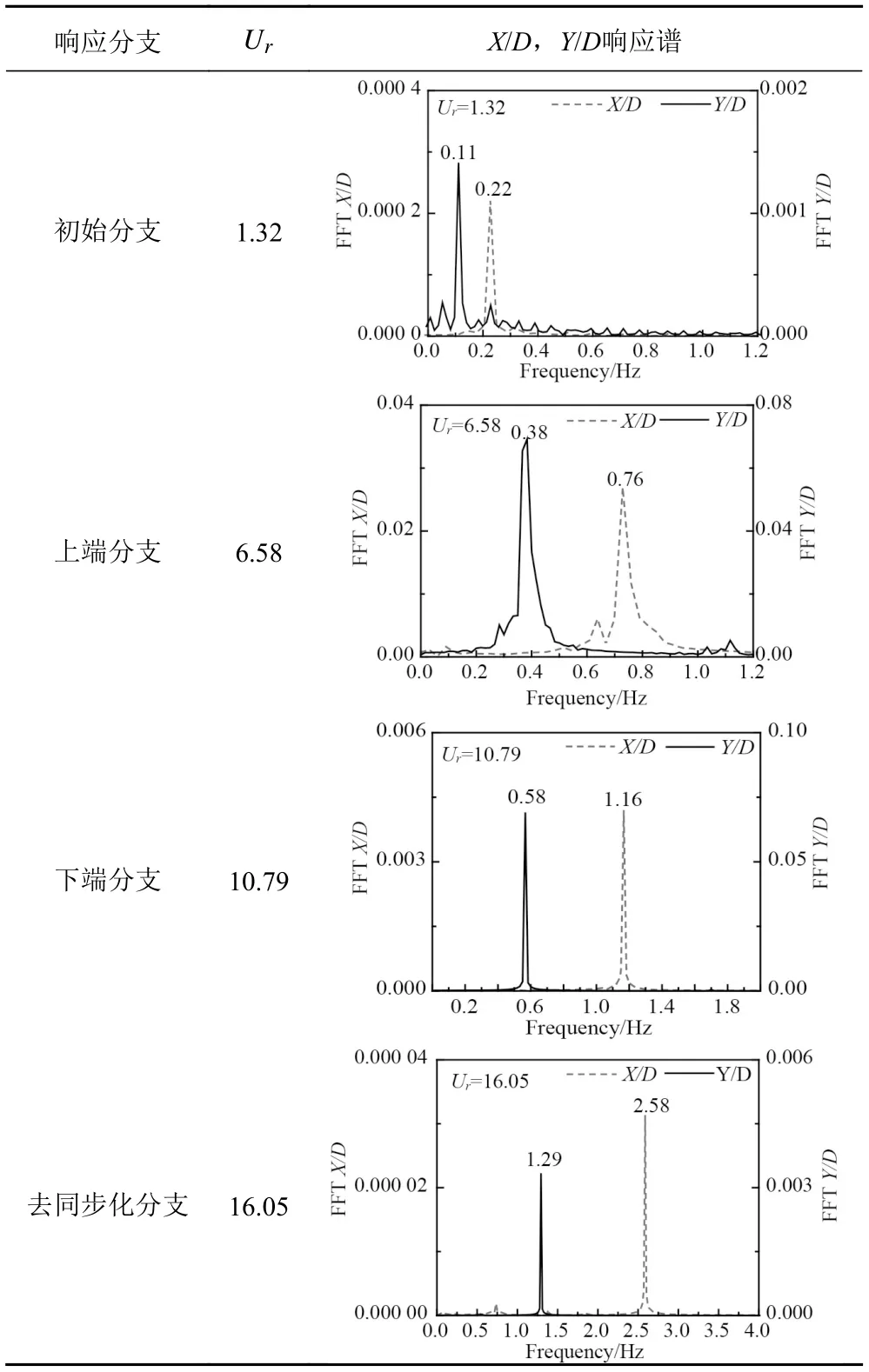
表3 浮式圆柱X/D、Y/D 涡激运动响应频谱图（m*=1）Tab. 3 Spectral diagram of X/D and Y/D vortex induced motion of floating cylinder（m*=1）

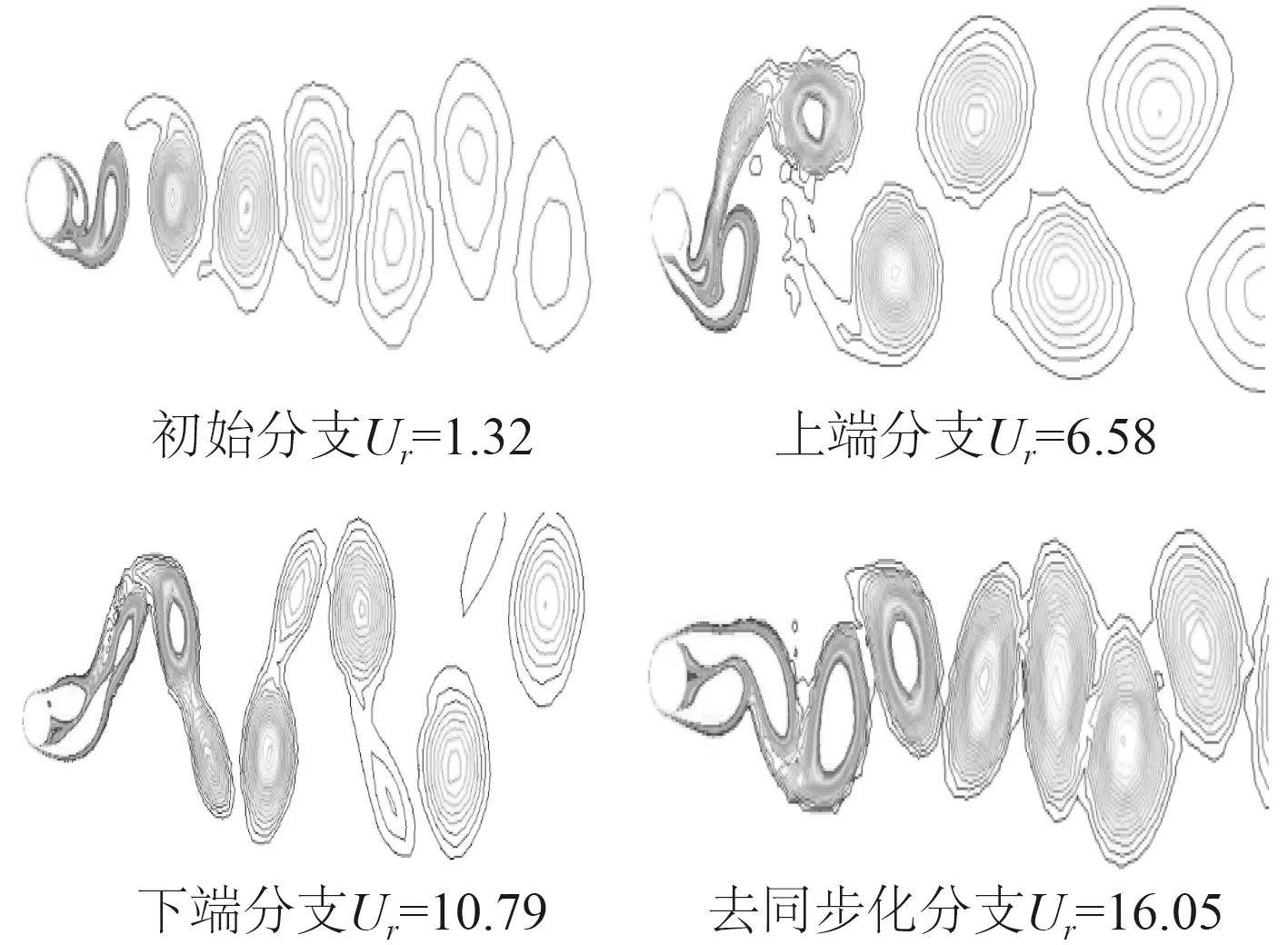
图7 浮式圆柱X/D，Y/D 涡激运动涡泄图Fig. 7 Vortex-exhaust diagram of floating cylinder X/D and Y/D vortex-induced motion

3 结 语

本文应用CFD 数值模拟方法对二维圆柱在不同流速下的涡激运动问题进行研究。

1）通过与Jauvtis&Williamson 在2004 年的经典实验结果的对比，数值计算可以较好模拟圆柱涡激运动，但在最大振幅方面有所低估。初始分支、上端分支和下端分支的运动轨迹与实验结果基本相似。数值模拟再现了实验中的S S， 2S， 2T和 2P涡泄模式。

2）浮式圆柱涡激运动的初始分支，表现为2 种不同的涡泄模式，分别为P+S模式和 2P模式。而质量比为2.6 的圆柱，在初始分支中涡旋泄放表现为S S模式和 2S模式。