基于属性的多授权中心身份认证方案

唐飞，包佳立，黄永洪，黄东，王惠莅

（1.重庆邮电大学计算机科学与技术学院，重庆 400065；2.重庆邮电大学网络空间安全与信息法学院，重庆 400065；3.重庆机电职业技术大学信息工程学院，重庆 402760；4.中国电子技术标准化研究院信息安全研究中心，北京 100076；5.西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071）

1 引言

身份认证技术作为网络空间安全的第一道关口，是网络空间环境确认操作者身份的有效方法，保证了用户与其数字身份的绑定关系。身份认证方案是一种交互过程，使持有私钥的证明者能够向持有相应公钥的验证者证明其合法身份。

身份认证方案的概念由Fiat 等[1]提出，方案中存在一个可信中心核实用户身份信息并为其生成私钥，用户可以利用该私钥向其他用户证明其身份的真实性。Schnorr[2]方案是经典的身份认证方案之一，其安全性依赖于离散对数的困难性。随后，Guillou 等[3]基于RSA（Rivest-Shamir-Adleman）问题提出了一种高效的身份认证方案。

为了简化传统公钥基础设施中的证书管理工作，Shamir[4]提出了基于身份的密码方案概念。在基于身份的密码方案中，将实体用户的身份信息作为公钥，并由一个可信的密钥生成中心（KGC,key generation center）生成用户的密钥。Kurosawa 等[5]根据BB04 签名方案[6]构建了一种基于身份的身份认证方案，并证明了方案在随机预言模型下的安全性。Chin 等[7]提出了一种在标准模型下可证明安全的身份认证方案。Barapatre 等[8]根据基于身份的密钥封装机制提出了一种基于身份的身份认证方案通用框架，并构造了一种具体的认证方案。

在基于身份的密码方案基础上，Sahai 等[9]进一步提出了基于属性的密码方案概念。以属性加密[9]为例，用户的密钥和密文都被标记了一个属性集合，当用户拥有的属性个数超过加密者预设的门限值时，用户可以对密文进行解密。属性密码提供了更加灵活的操作关系，受到了国内外学者的广泛研究，例如基于属性的加密方案[10-11]、基于属性的签名方案[12-15]、基于属性的密钥交换协议[16-17]等。基于属性密码的优良性质，显然可以考虑其在身份认证领域的应用。Anada 等[18]将属性密码推广到身份认证方案中，定义了证明者策略和验证者策略2 类基于属性的身份认证方案，并基于属性密钥封装机制实现了属性身份认证方案的通用构造，给出了一种具体的实现方案。

在基于属性的密码方案中，也需要一个可信的密钥生成中心来生成用户的私钥。因此，用户需要相信中心不会泄露用户私钥。此外，单个密钥生成中心也面临攻击风险过高和负担过重等问题。事实上，Chase[19]于2007 年就提出了多授权中心属性加密方案的概念。在他的方案中，用户私钥的生成由多个授权中心共同完成，但方案仍需要一个可信中心对用户身份信息进行统一认证以防多用户的合谋攻击。为了解决这一问题，Lin 等[20]结合分布式密钥生成技术[21]提出了一种不依赖任何可信中心的门限多授权中心属性加密方案。

针对无可信中心环境下的属性身份认证需求问题，在Anada 等[18]所提出的基于属性的身份认证框架基础上，本文提出多授权中心的属性身份认证方案。本文主要贡献如下。

1) 定义了基于属性的多授权中心身份认证方案的概念，具体包括初始化算法、密钥生成算法和认证协议3 个部分。与单授权中心属性身份认证的不同之处在于，用户的私钥由n个授权中心中的至少t个共同完成，且方案最多可以抵抗来自t-1 个授权中心的合谋攻击，具有较高的安全性。

2) 基于双线性映射构造了一种属性身份认证方案。该方案支持门限谓词策略，即证明者的属性集与验证策略属性集的交集个数至少需要满足预定的门限值。分析了方案在分布式密钥生成环境下的安全性，并从计算开销、通信开销等方面分析了方案的效率。此外，与同类型认证方案的比较结果表明，所提方案具有更优良的综合性能。

3) 以多因子身份认证为例，分析所提方案在电子凭据应用场景中的可行性。以口令、邮箱、生物特征等因子构成用户的属性集，用户获得属性集相关的私钥。在身份认证过程中，验证者指定验证策略属性集，并规定验证者需满足的属性个数门限值，从而实现基于用户多因子的身份认证机制。

2 预备知识

2.1 双线性对

定义1令G和GT是2 个阶为大素数p的乘法循环群，其中g是群G的生成元。双线性对e:G×G→GT是满足如下性质的映射。

1) 双线性。对于任意a,b∈Zp，有e(g a,gb)=e(g,g)ab。

2) 非退化性。存在g c,gd∈G，使e(g c,gd) ≠1GT，其中1GT代表群GT的单位元。

3) 可计算性。存在有效的算法对任意a,b∈Zp，可计算e(g a,gb)。

2.2 方案定义

基于属性的多授权中心身份认证方案包括3 种算法或者协议，分别是初始化（Setup）算法、密钥生成（Key-generation）算法和认证协议。其中，初始化算法根据安全参数得到系统公开参数；密钥生成算法根据用户的属性集生成相应的属性密钥；认证协议由证明者P 和验证者V 共同完成。基于属性的多授权中心身份认证方案的具体定义如下。

初始化。输入安全参数λ和属性全集U，生成系统公开参数params。同时，每个授权中心iP根据系统参数params 进行相应的初始化，得到自己的主密钥ski。

密钥生成。输入系统参数params 和用户属性集合I，如果用户有资格获得这些属性，则向至少t个授权中心iP请求生成部分密钥，用户在获得至少t个部分密钥之后，合成自己的属性密钥集Dj，其中j∈I。

认证协议。证明者P 拥有参数(params,I,DI)作为输入，验证者V 拥有参数(params,I*)作为输入，其中I*是 V 选择的验证策略属性集。如果|I∩I*|≥k，则P 能正确证明其身份信息，V 输出1；否则，V 输出0。其中，k为策略所规定的门限值。

2.3 安全模型

基于属性的身份认证方案需满足不可仿冒性和匿名性。

1) 不可仿冒性

在不可仿冒性定义中，敌手首先与诚实证明者运行认证协议，随后尝试向第三方仿冒其为一个合法证明者。Anada 等[18]称这类针对属性身份识别方案的攻击为中间人攻击。

初始化阶段。挑战者C 输入安全参数λ，运行Setup 算法得到系统参数params，并将params 发送给敌手A 。同时，根据params 对所有授权中心T1,…,Tn进行初始化。

询问阶段。敌手A 可以发起如下询问。

①密钥生成询问。在接收到系统参数params后，敌手A 向挑战者C 发出属性集合I密钥生成请求，C 返回相应属性密钥DI。询问密钥生成的属性集合I不能满足攻击目标属性集合I*的要求，即|I∩I*|＜k。

② 交互训练。敌手A 作为恶意验证者V*和诚实证明者P 交互运行认证协议。

挑战阶段。敌手A 作为恶意证明者P*和任意的诚实验证者V 进行交互，试图说服验证者接受。

如果任意多项式时间敌手A 都不能以不可忽略的优势使诚实验证者接受，则称基于属性的多授权中心身份认证方案具有不可仿冒性。

2) 匿名性

基于属性的多授权中心身份认证方案的匿名性表示拥有属性集I的证明者在向验证者证明后，除了会泄露|I∩I*|≥k这一事实外，不会泄露其他任何属性信息。基于属性的多授权中心身份认证方案的匿名性的具体定义如下。

初始化阶段。挑战者C 输入安全参数λ，运行Setup 算法得到系统参数params，并将params 发送给敌手A 。同时，根据params 对所有授权中心P1,…,Pn进行初始化。

询问阶段。敌手A 可以发起密钥生成询问。在接收到系统参数params 后，敌手A 向挑战者C发出属性集合I密钥生成请求，C 返回相应属性密钥DI。

挑战阶段。敌手A 与挑战者C 进行如下操作。

①敌手选择3 个属性集(I0,I1,I*)，其中I0和I1表示2 个证明者身份属性集，I*表示用于挑战的验证策略属性集，且|I0∩I*|≥k，|I1∩I*|≥k。

② 挑战者运行密钥生成算法生成密钥DI0和DI1，并将2 个私钥发送给敌手。

③挑战者随机选择b∈{0,1}，并充当证明者P使用私钥DIb与敌手交互运行认证协议。

④ 最后，敌手输出猜测值b'，如果b'=b，则表示敌手猜测成功。

本文将上述游戏中敌手的成功优势定义为|Pr[b'=b]-1/2|。如果任意多项式时间敌手A 都不能以不可忽略的优势区分证明者P 用的是私钥DI0还是DI1，则称基于属性的多授权中心身份认证方案具有匿名性。

3 具体方案

本文方案主要借鉴了Li 等[22]的属性签名方案。Li 等[22]构造了一种支持门限谓词的中心化属性签名方案。为了实现无可信中心环境下的用户属性密钥生成，本文采用分布式密钥生成（DKG,distributed key generation）技术[21]。分布式密钥生成技术是门限密码系统的主要组成部分，主要通过多方参与的形式来计算共享的公钥和私钥集，不需要依赖任何可信第三方，其核心思想是(t,n)门限秘密共享。秘密共享用于在一组参与者中共享一个秘密，每个参与者都有关于秘密的部分信息。门限秘密共享意味着n个参与者之间的至少t个参与就可以重建秘密值。在DKG 协议中，参与者共同选择并生成一个随机秘密共享值s。每个参与者Pi选择一个随机共享值si，然后至少t个参与者参与就可以恢复出秘密共享值s，并公开值y=gs。本文将系统的主密钥当成秘密共享值s，只要有t个参与者就可以重建主密钥，同时在系统中公开系统主公钥y=gs。

由阈值门组成所有谓词γ。具体地，支持阈值k为 1～d2的所有谓词γk,I*(·) →0/1，其中。

回顾关于拉格朗日插值的知识，给定d-1次多项式上的d个点q(1),…,q(d)，则可以利用拉格朗日插值公式来计算q(i)，其中i∈Zp。设S为d元素集，在q(i)的计算中，将q(j)的拉格朗日系数Δj,S(i)定义为

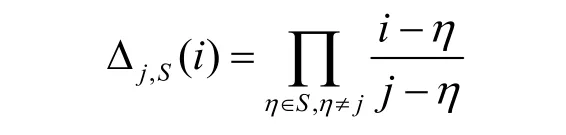
3.1 详细过程

本节将描述基于属性的多授权中心身份认证方案，该方案由以下3 个阶段组成。

初始化（Setup），系统初始化阶段。

1) 根据安全参数λ生成素数阶p。选择2 个阶为素数p的乘法循环群G和GT，g是群G的生成元，双线性映射e:G×G→GT。定义属性全集为U，默认属性集A中有a-1个属性元素。选取哈希函数为H:{0,1}*→G。系统公共参数为

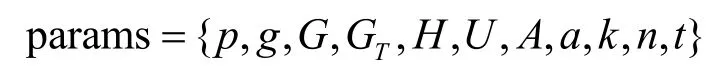
其中，属性门限值为k∈[1,a]，n为授权中心的个数，t为用户属性密钥生成的门限值。

2) 生成系统主密钥。

Step1iP选择一个t-1 阶的多项式

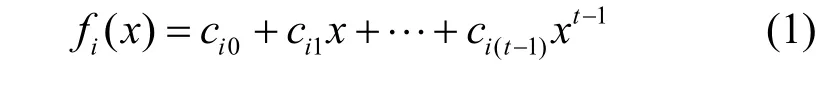
然后，Pi分别计算并广播Cik=gcik(modp)，其中k=0,…,t-1。接着Pi计算秘密值yij=f i(Pj)，其中j=1,…,n，并将其发送给jP，其中j≠i。

Step2Pj验证等式是否成立，如果成立，则认为Pi为诚实的中心；否则，Pj要求Pi重新广播yij。

Step3由此，可以得到系统的主密钥

其中，S表示参与密钥生成的t个中心。从而得到系统主公钥y=gs。

3) 系统中的所有授权中心根据系统参数共同生成参数g2∈G。

Step1Pi选择一个n-1 阶的多项式

然后，Pi分别计算并广播Bik=gbik(modp)，其中k=0,…,n-1。接着Pi计算秘密值t ij=hi(Pj)，其中j=1,…,n，并将其发送给Pj，其中i≠j。

Step2Pj验证等式是否成立，如果成立，则认为Pi为诚实的中心；否则，要求Pi重新广播tij。

Step3经过上面的交互，每个授权中心都可以计算参数

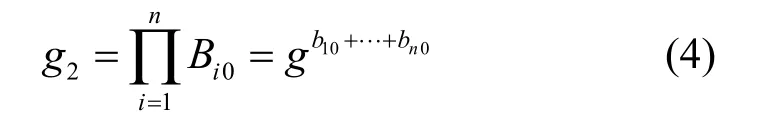
然后，生成参数Z=e(y,g2)。

4) 公开系统参数params={p,g,g1,Z,G,GT,H,U,A,a,k,n,t}，其中，属性门限值k∈[1,a]，n为授权中心的个数。

密钥生成（Key-generation），为属性i∈I生成相应的属性私钥Di。

1) 生成一个新的属性集=I∪A。对于每个j∈，Pi选择一个随机值rij∈Zp，并计算

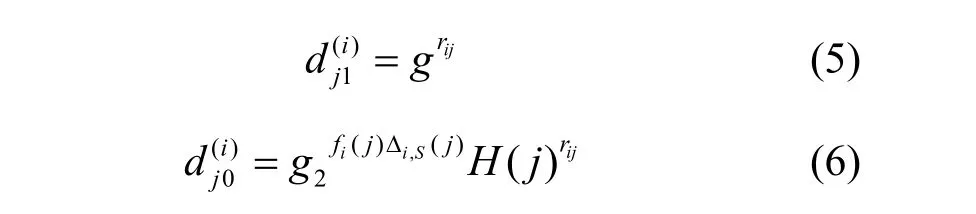
2) 用户收到t个中心发来的部分密钥后，计算自己的属性私钥

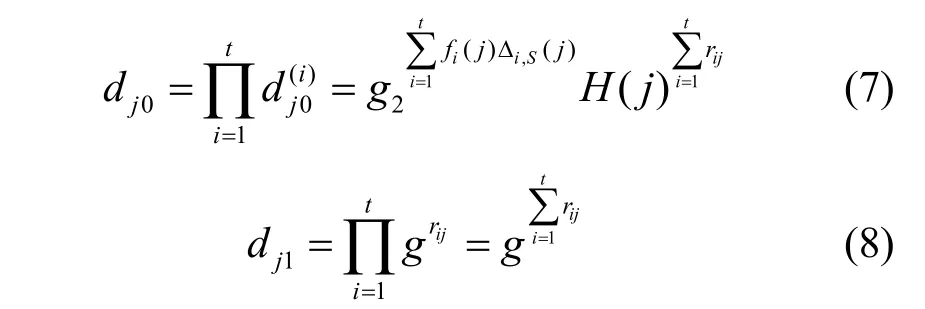
由此得到每个属性j∈Iˆ的私钥Dj=(d j0,dj1)。

认证协议。为了完成身份认证过程，即证明用户拥有验证策略属性集I*中的至少k个属性。首先，用户选择一个含有k个属性的属性子集I′⊆I∩I*，并进行以下操作。

1) 用户选择一个默认属性子集A′⊆A，其中=a-k并且选择m+a-k个随机值ri′∈Zp，其中i∈I*∪A′，并随机选择x∈Zp，计算

然后，将(σi,σ0′)发送给验证者。

2) 验证者随机选择c∈Zp，并发送给用户。

3) 用户收到c后，计算

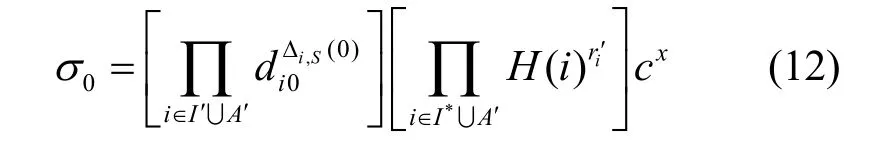
并将σ0发送给验证者。

3.2 正确性分析

首先，所提方案的系统初始化和密钥生成2 个算法的正确性可通过分布式密钥生成技术的正确性得以保证。其次，交互验证协议的正确性如下。

4 方案分析

4.1 安全性分析

本文方案采用的是Gennaro等[21]的分布式密钥生成方法，该方法已经被证明是抗合谋的。因此，本文方案可以最多抵抗来自t-1 个授权中心的合谋攻击。此外，分布式密钥生成技术核心在于以一种隐式的方式恢复系统主密钥s，从而得到用户的属性私钥。因此，不同于Chase[19]的各授权中心负责一个或多个属性密钥生成，基于分布式密钥生成技术的用户属性密钥生成机制可以抵抗来自用户的合谋攻击。

如前所述，本文方案主要基于文献[14]的单授权中心属性签名方案。借鉴文献[22]的混合证明思路，可以将本文方案的不可仿冒性和匿名性分别规约到文献[14]方案的不可仿冒性和签名者隐私性上。规约方法具体如下，首先定义如下3 个游戏。

1) 游戏Game0。与不可仿冒性和匿名性安全定义一样，所有参与方均诚实执行相关算法或协议。

2) 游戏Game1。将系统主密钥定义为y=gas，其中，指数a是文献[14]方案中CDH（computational Diffie-Hellman）问题的一个挑战实例；指数s是所有授权中心联合生成的随机秘密值，但所有授权中心均不知道s的具体值，除非至少t个授权中心发起合谋攻击。

3) 游戏Game2。在该游戏中，系统主密钥依然为y=gas，与Game1的区别在于，在Game2中，挑战者充当授权中心角色，知道秘密值s。

由此，可以证明任意多项式时间敌手的优势在上述3 个游戏中是计算不可区分的。

引理1如果文献[21]的分布式密钥生成技术是安全的，则敌手在游戏Game0与Game1中的优势是计算不可区分的。

证明根据分布式密钥生成技术[21]的安全性结论可知，即便t-1个参与者发起合谋攻击，依然不能区分元素y=gs∈G是由n个参与者协作生成的还是从群G中随机选择得到的。因此，任意多项式时间敌手都无法区分元素y:=gs∈G和y:=gas∈G，其中s是分布式密钥生成技术的真实值，a是CDH 问题实例中的指数，且a与s是相互独立的。因此，对任意多项式敌手而言，其在游戏Game0与Game1中的优势是计算不可区分的。

证毕。

引理2任意多项式敌手在游戏Game1与Game2中的优势是计算不可区分的。

证明 注意，在2 个游戏中，系统主公钥均为y=gas，其中s是分布式密钥生成技术的真实值，a是CDH 问题实例中的指数，且a与s是相互独立的。因此，尽管挑战者知道值s，但是y=gas依然是群G中的一个随机元素，对敌手而言挑战者是否知道s并不会影响敌手的攻击。

证毕。

基于上述2 个引理，可以分别证明本文方案的不可仿冒性和匿名性。

1) 不可仿冒性

首先证明引理3。

引理3如果文献[14]的属性签名方案具有不可仿冒性，则任意多项式时间的仿冒攻击敌手在游戏Game2中的优势是可忽略的。

证明将本文方案记为ABI，仿冒攻击敌手为A，挑战者为C；将文献[14]的单授权中心的属性签名方案记为ABS，伪造敌手记为A'，挑战者记为C'。将ABI 方案的不可仿冒性规约到ABS 的不可仿冒性，ABI 的挑战者C 同时也充当ABS 方案的敌手A'，C 尝试利用敌手A 仿冒攻击ABS 方案的安全性。具体证明过程如下。

初始化阶段。挑战者C 输入安全参数λ，运行Setup 算法得到系统参数params。同时，根据参数params 运行分布式密钥生成算法生成y=gs。此外，从挑战者C'处获得 CDH 问题挑战实例(g a,gb)。最后，将系统主公钥设置为y=gas，并将系统公开参数发送给敌手A。

询问阶段。敌手A 可以发起如下询问。

①密钥生成询问。敌手A 向挑战者C 发出属性集合I密钥生成请求。收到请求后，C 将属性集合I发送给ABS 的挑战者C'。根据ABS 方案的不可仿冒性证明，C'会返回相应的属性密钥DI。C 直接将ID返回给敌手A 即可。

②交互训练。敌手A 作为恶意验证者V*和诚实证明者P 交互运行认证协议，挑战者C 在这里需要充当证明者P 向敌手A 提供认证操作。当敌手发送挑战值c给挑战者时，挑战者将c充当消息发送给ABS 方案的挑战者C'，根据ABS 方案的不可仿冒性证明，C'会返回一个合法签名。最后，挑战者C 将签名作为挑战回复返回给敌手A。因为签名是有效的，所以其一定能通过验证协议。

挑战阶段。敌手A 作为恶意证明者P*和任意的诚实验证者V 进行交互，试图说服验证者接受。在这里，挑战者C 充当验证者V，选择挑战值c*发送给敌手A。

最后，如果敌手A 能成功打破ABI 方案的不可仿冒性，则表示其能生成关于挑战值c*的有效验证信息(σi,σ0′,σ0)，使其通过验证等式

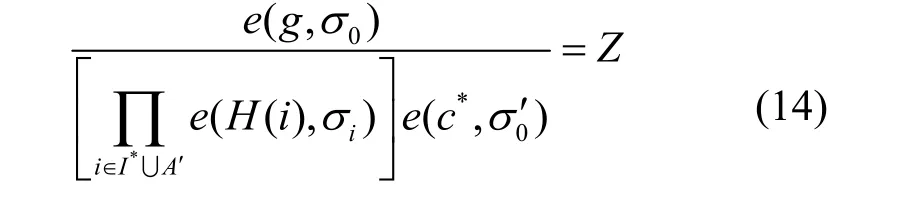
因此，挑战者C 将c*作为挑战消息，并输出(c*,σi,,σ0)作为ABS 方案的伪造签名。最后，根据ABS方案的不可仿冒性证明可知，C'会根据C的伪造输出值T=gasb，C计算Ts-1即可得到给定CDH 问题实例的解gab。

证毕。

根据引理1～引理3，即可得到定理1。

定理1如果文献[21]的分布式密钥生成技术是安全的，且文献[14]的单授权中心属性签名方案具有不可仿冒性，则本文方案具有不可仿冒性。

2) 匿名性

匿名性的证明类似于上述不可仿冒性证明，唯一区别是将本文方案的匿名性规约到单授权中心的签名者隐私性上。事实上不难发现，属性身份认证方案的匿名性要求与属性签名方案的签名者隐私性要求是一致的。因此，本文直接给出定理2。

表1 方案效率对比

定理2如果文献[21]的分布式密钥生成技术是安全的，且文献[14]的单授权中心属性签名方案具有签名者隐私性，则本文方案具有匿名性。

4.2 效率分析

本节分析本文方案的效率，包括计算开销和通信开销。系统成功建立后，就不会再运行初始化算法。此外，用户获得属性密钥后，也不再需要运行密钥生成算法。因此，本文不考虑初始化算法和密钥生成算法的计算和通信开销。

在基于双线性映射的密码方案中，双线性对运算、map-to-point 运算、群元素指数运算和群元素乘法运算是消耗最大的4 种运算，因此本文只考虑这4 种运算的开销。将这4 种运算的计算开销分别记为Tpar、Tmtp、Texp、Tmul，并基于这4 种运算考虑本文方案各算法的开销。

将本文方案与同类型的方案进行效率对比。目前，尽管只有一篇基于属性的身份认证方案的文献[18]，但是，基于属性签名方案也可以实现属性身份认证方案。所以，本文也将相关属性签名方案进行对比。本文主要关注多授权中心的属性身份认证方案，因此不比较文献[18]的方案。此外，本文方案基于文献[14]的属性签名方案，所以计算开销和通信开销与文献[14]的方案均一致。事实上，文献[14]也考虑了多授权中心，其方法主要基于Chase[19]的多授权中心方法，因此需要一个额外的可信中心对用户进行统一认证，以防合谋攻击。文献[23]构造的多授权中心属性签名方案与文献[14]的方案核心技术类似，方案的计算开销与通信开销一致。文献[24-26]的多授权属性签名方案与本文方案采用的技术不一样，因此将本文方案与文献[24-26]的方案进行效率对比，并参考文献[27]的效率分析形式，对比结果如表1 所示。

表1中，m表示验证策略属性集中的属性个数，k表示策略门限值，l表示每个权威的访问结构中包含的属性，τ表示集合中元素的个数。

接下来，分析本文方案与文献[24-26]方案在传输带宽方面的需求对比，并参考文献[27]的效率分析形式，对比结果如表2 所示。

表2 方案通信开销对比

表2 中，|G|表示群G中的元素长度，|GT|表示群GT中的元素长度。

5 多因子身份认证应用

本节考虑本文方案在电子凭据中的多因子身份认证应用。

正如文献[28]所说，随着“互联网+”时代的到来以及电子商务的快速发展，纸质凭据的成本高、难以管理等问题越来越明显，电子凭据以其高效、成本低廉和绿色环保等优点受到人们的青睐。凭据是日常生活中被用作证明物品的东西，包括电子发票等。电子凭据作为纸质凭据的一种电子化产物，具有相同的效用。

电子凭据的流程包括电子凭据的开具、查验以及查询等业务，不同的业务所需的操作权限等级不同。同时，电子凭据涉及用户大量的敏感信息，保护用户敏感信息是对电子凭据业务所提出的挑战。为了保证电子凭据相关业务的正确执行，确保电子凭据生成和使用的合理性，需要确认操作者的权限，并对操作者进行身份认证。

众所周知，单因子身份认证具有不灵活、不支持细粒度身份认证等问题。为了解决这一问题，张敏等[29]提出将生物特征、口令、邮箱3 种因子或者任意其中2 种结合进行身份认证，形成多因子的身份认证方案。多因子身份认证方案的提出提高了认证方案的安全性。

文献[28]针对电子凭据业务中身份认证的需求，提出了多元认证方案。在该方案中，根据用户提交的身份信息、应用场景描述、所需权限描述等，系统为其分配不同类型的认证方式，例如口令认证、指纹识别、人脸识别等。本文方案根据用户口令、邮箱、生物特征、访问权限等因子构成用户的属性集，通过属性谓词策略判断用户属性集是否满足验证策略要求，以此来完成身份认证，从而可以实现基于属性的细粒度认证方式。基于本文方案的电子凭据中的身份认证模型如图1所示，具体过程如下。

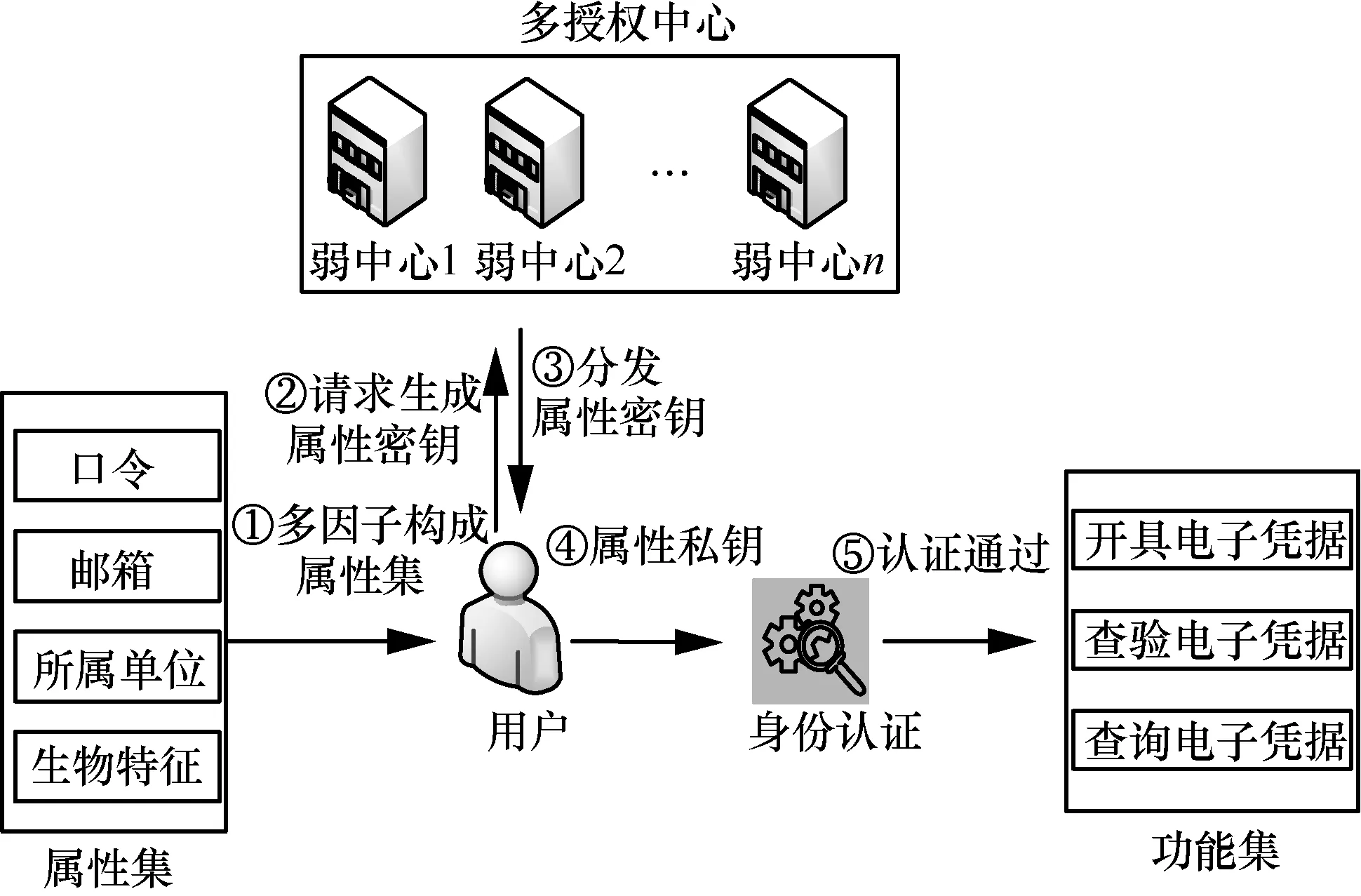
图1 基于本文方案的电子凭据中的身份认证模型

1) 电子凭据管理系统中的用户根据口令、邮箱、所属单位、职务、角色、生物特征等因子构成自己的属性集。

2) 用户根据属性集向n个授权中心中的至少t个授权中心发出属性密钥生成请求。授权中心在收到用户发出的请求后，根据所提交的属性集为属性集中的属性生成相应的部分密钥，并将其发送给用户。

3) 用户在收到来自t个授权中心发送来的部分密钥后，自己合成属性私钥。

4) 用户利用属性私钥通过认证协议证明自己身份的合法性，即拥有对电子凭据进行某操作的权限，例如，开具电子凭据、查验电子凭据或者查询电子凭据。在认证协议中，电子凭据系统需要指定进行不同电子凭据操作所需要的验证策略属性集，并规定所需要满足的属性个数门限值。如果用户所提交的属性集与需要进行某项操作所指定的验证策略属性集的交集的属性个数达到属性个数门限值，则用户身份合法，身份认证成功；否则，身份认证失败。

5) 身份认证成功后，用户可以进行相应操作。例如用户需要查询电子客票信息时，提供相应的属性私钥通过身份认证即可查询电子凭据。

6 结束语

本文定义了基于属性的多授权中心的身份认证的概念，并基于双线性映射构造了一种高效的属性身份认证方案。在该方案中，根据用户的身份属性信息构成用户的属性集合，结合分布式密钥生成技术实现用户属性私钥的生成，并通过门限谓词策略规定认证机制，分析了所提方案的安全性、不可仿冒性和匿名性。此外，还考虑了基于属性身份认证方案在电子凭据中的多因子认证应用。