基于优化预测控制的VIENNA整流器研究

（南京工业大学电气工程与控制科学学院，江苏南京211816）

VIENNA整流器除了具有功率因数高、开关器件少、以及功率密度高等特点外，还有电网不平衡等特殊条件下仍然可以工作、谐波抑制特性好等优点。对提供电动汽车充电的直流充电桩而言，采用VIENNA整流器作为直流充电桩的前级整流模块，是较理想的选择，具有很高的研究意义和实际应用价值[1]。

当下对三相VIENNA整流器的研究主要从脉冲调制技术和控制策略等方面入手。针对控制策略研究方面，主要由比例积分（PI）控制、平均电流控制、单周期控制和直接功率控制等[2]。PI控制算法简单，物理意义明确，易于实现，但在系统启动与负载突变等情况下动态特性较差，对系统参数选取也有很高的要求[3]。本文提出了优化预测控制控制策略，外环采用功率预测控制[4]，并引入准比例谐振（QPR）电流控制，内环采用无差拍控制策略。以三相三电平VIENNA整流器为主拓扑，利用Matlab/Simulink软件以及搭建实验模型验证分析其可行性，与传统双闭环控制进行对比，通过对仿真波形的对比以及实验验证分析可知，优化预测控制下的VIENNA整流器继承了传统双闭环控制策略的优点，提高了直流侧的抗扰性和平稳性，使得整流器处于单位功率因数运行。

1 VIENNA整流器数学建模

三相三电平VIENNA整流器的拓扑结构如图1所示，VIENNA整流器的工作状态由双向功率开关管开关状态和输入电压的相位决定。

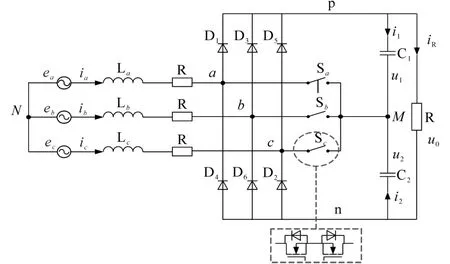
图1 三相三电平VIENNA整流器原理图Fig.1 Principle diagram of three-phase three-level VIENNA rectifier

建立VIENNA整流器的数学模型。定义[5]：双向开功率关管Sa,Sb,Sc，简 记SK(K=a,b,c)；uaM,ubM,ucM分别是VIENNA整流器的整流桥臂输入节点（a点、b点、c点）到直流侧中性点M之间的电压，简记uKM(K=a,b,c)。SK=1表示该双向开关管是导通的，SK=0表示该双向开关管是关断的；SKp=1表示VIENNA整流器的上桥臂二极管导通，SKp=0表示VIENNA整流器的上桥臂二极管关断；SKn=1表示VIENNA整流器的下桥臂二极管导通，SKn=0表示VIENNA整流器的下桥臂二极管关断。为了方便计算，分别推导出各个坐标系下的数学模型如下。

1.1 abc坐标系下VIENNA整流器的数学模型

1.2 α- β坐标系下VIENNA整流器的数学模型

VIENNA整流器在α-β坐标系下动态模型方程为

1.3 d-q坐标系下VIENNA整流器的数学模型

2 VIENNA整流器的控制策略

本文提出优化预测控制的控制策略，外环采用功率预测控制，并引入准比例谐振（QPR）电流控制，内环采用无差拍控制策略。

2.1 无差拍控制

网侧输入处于平衡状态时，三相VIENNA整流器可以等效成单相模型[6-7]，如图2所示。

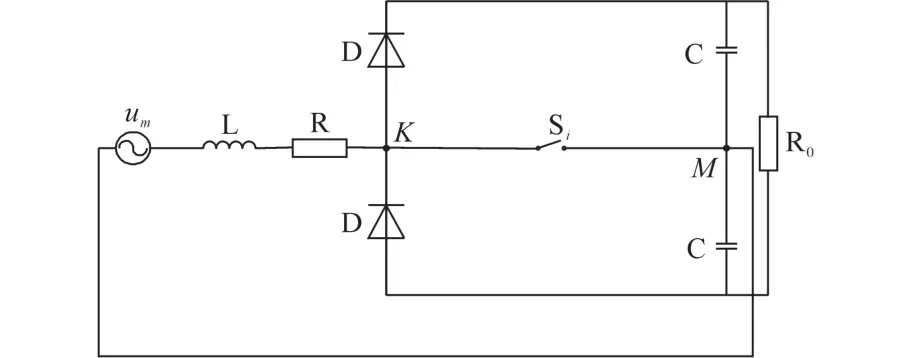
图2 三相VIENNA整流器单相等效模型Fig.2 Single-phasee quivalent model of three-phase VIENN Arectifier

假定开关管均为理想器件，忽略电路中的等效电阻R。当功率开关管开通时：

图3为开关开通、关断情况下电感电流波形。

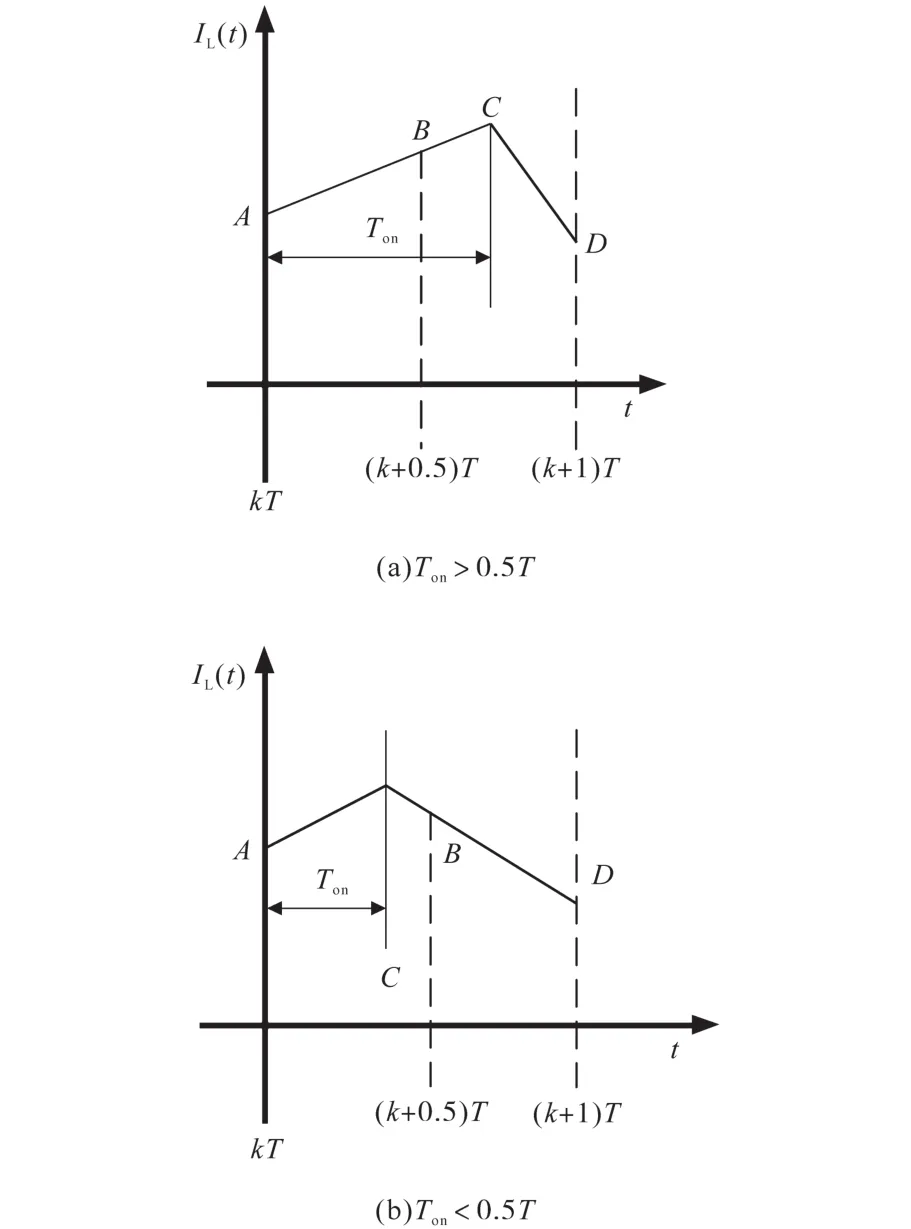
图3 开关开通、关断情况下电感电流波形Fig.3 Inductor current waveforms under switching on and off

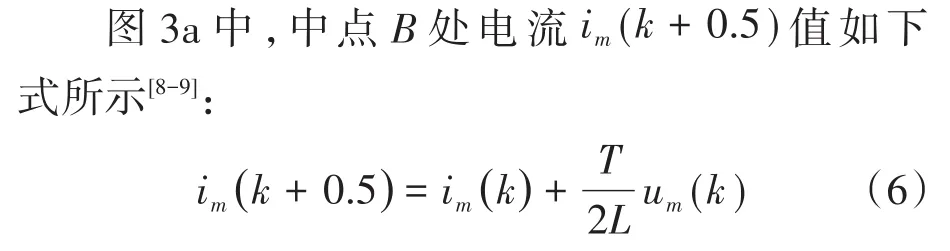
2.2 准比例谐振QPR控制策略

理想谐振变换器与比例控制部分相结合，形成比例谐振（proportional resonance，PR）。非理想谐振变换器与比例控制部分相结合，形成准比例谐振（QPR）。比例谐振控制器同重复控制相似，属于一种基于内模原理的控制，其传递函数如下：

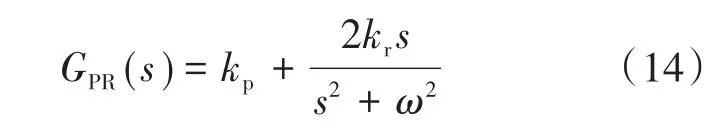
式中：kp为比例系数；kr为谐振系数；ω为谐振频率。

PR调节器从数学分析和计算方面上是完全无损的，可以实现信号跟踪的无差性；但是PR调节器带宽太小，在实际应用时波动点增益较小，无法达到无穷大的增益，严重影响幅值跟随效果，并且系统的稳定性和增益成反比。为了解决PR调节器存在的问题，常采用准比例谐振QPR控制器，其传递函数为

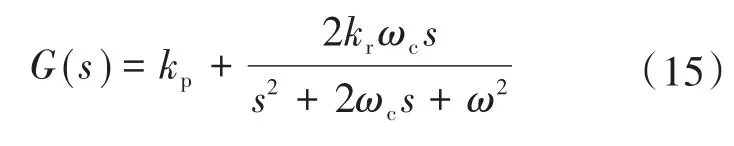
式中：ωc为截止频率。

根据式（15）得到QPR的结构框图如图4所示，QPR控制中参数值分别为：kp=1,kr=10,ω=100π,ωc=10 rad/s。

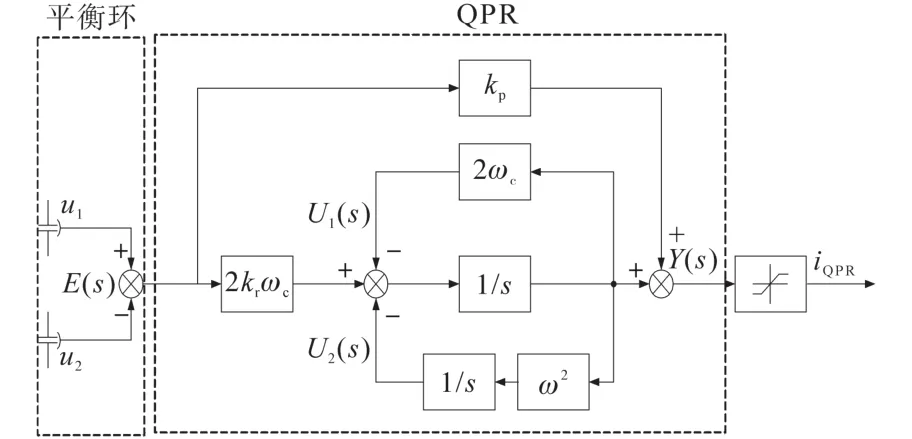
图4 准比例谐振的结构框图Fig.4 Structure block diagram of quasi-proportional resonant

2.3 功率预测控制

2.3.1 传统功率预测控制

2.3.2 优化功率预测控制

优化预测控制框图如图5所示。优化预测控制策略外环在基于功率预测控制基础上引入了准比例谐振控制iQPR，这有利于提高平稳性和动态性能；内环部分引入无差拍控制，提高了系统的动态性能和跟踪精度。

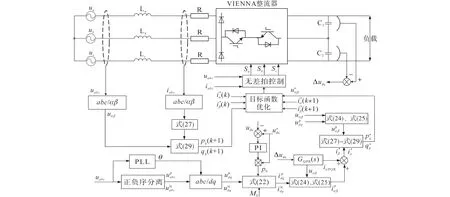
图5 优化预测控制框图Fig.5 Optimized predictive control block diagram

3 仿真分析

为了验证提出的控制策略具有很好的动态性能和抗扰性，本文在Matlab环境下搭建了VIENNA整流器仿真模型，主要参数为：输入相电压有效值Um=220 V，直流侧输出电压Udc=800 V，输出功率P0=16 kW，开关频率fs=50 kHz，采样频率fr=50 kHz，交流侧滤波电感L=2 mH，直流侧稳压电容C1=C2=4 700 μF，优化预测控制的效果与传统双闭环控制做对比。

图6为输入电压、电流仿真波形，从图6可以看出，三相VIENNA整流器的输入侧电压、电流同相位，满足单位功率因数运行。

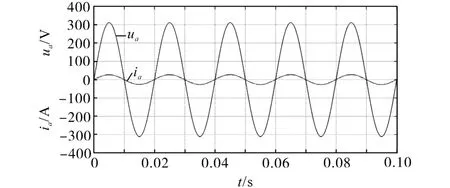
图6 输入电压电流仿真波形Fig.6 Input voltage and current simulation waveforms

图7为负载突变时在两种不同控制策略下输出侧电压仿真波形图。当负载在1 s时刻发生突变时，从图7a和图7b可以发现：采用传统双闭环控制时，在1 s处输出侧电压发生的突降在14 V左右，经过0.08 s恢复到稳定状态；采用优化预测控制时，在1 s处输出侧电压发生的突降在5 V左右，经过0.03 s恢复到稳定状态。这反映了传统双闭环控制和优化预测控制对负载突变都具有良好的抗扰性，在动态性能、抗扰性和稳定性方面，优化预测控制都显得较好一些。

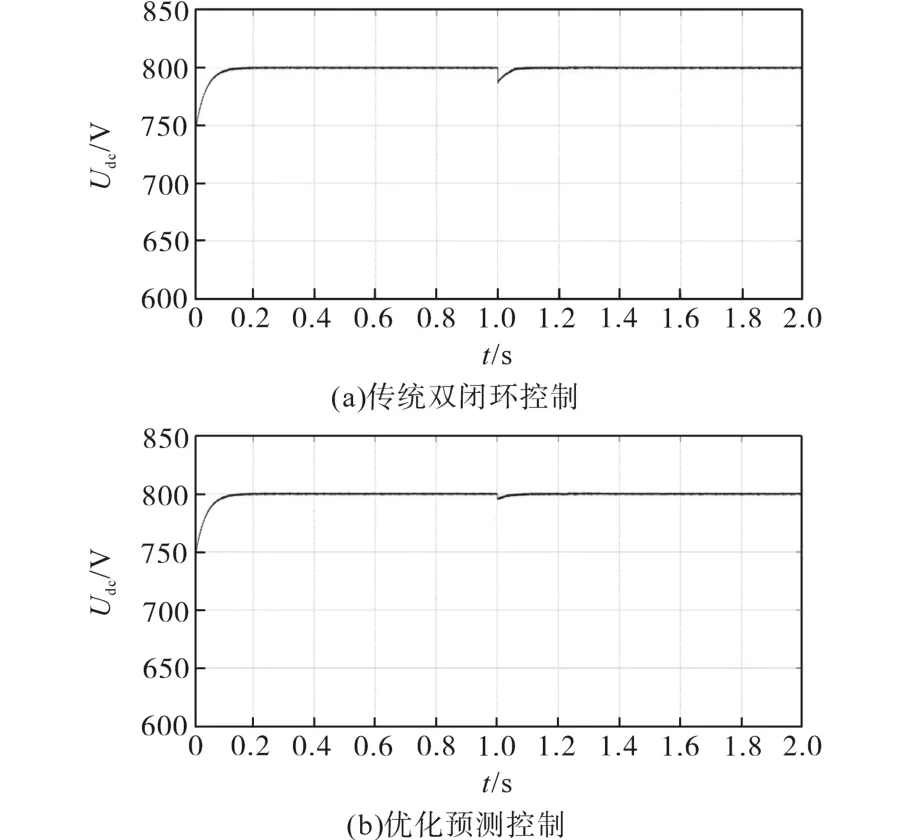
图7 负载突变时输出侧电压仿真波形Fig.7 Simulation waveforms of output side voltage when load changes abruptly

4 实验验证

通过理论推导及分析结果，搭建了一台15 kW的实验样机，实验参数设置和仿真参数相同，控制电路采用型号为TMS320F2812控制芯片。

图8为三相VIENNA整流器网侧输入电压、电流实验波形。从图8中可以看出，输入电流、输入电压同相位，输入电流跟随性很好，满足单位功率因数运行要求。

图8 三相输入电压、电流实验波形Fig.8 Experimental waveforms of three-phase input voltage and current

当负载发生突变时，直流侧输出电压的实验波形情况如图9所示。从图9中可以看出，在传统双闭环控制下，从平衡态突降了大概10 V左右，经过0.10 s恢复到稳定状态；在优化预测控制下，从平衡态大概突降了6 V左右，优化了约50%，经过0.06 s恢复到稳定状态，进一步说明了优化预测控制的抗扰性较好，平稳性较好，与仿真结果相符。

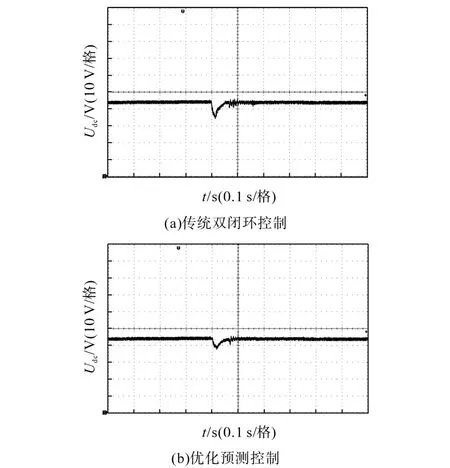
图9 负载突变时直流侧输出电压实验波形Fig.9 Experimental waveforms of DC side output voltage under sudden load change

当网侧输入电压不平衡时，直流侧输出电压波形如图10所示。在网侧输入电压发生故障，由平衡态转换到不平衡态时，在传统双闭环控制下直流侧输出电压发生振荡，而在优化预测控制下直流侧输出电压发生突降，约6 V左右。传统控制相较于优化预测控制，同样的故障情况下，尽管直流侧输出电压维持在800 V附近波动，但振荡比较大，从经典控制理论上讲，这是不平衡的，平稳性较差，而优化预测控制的实验波形平稳性较好。

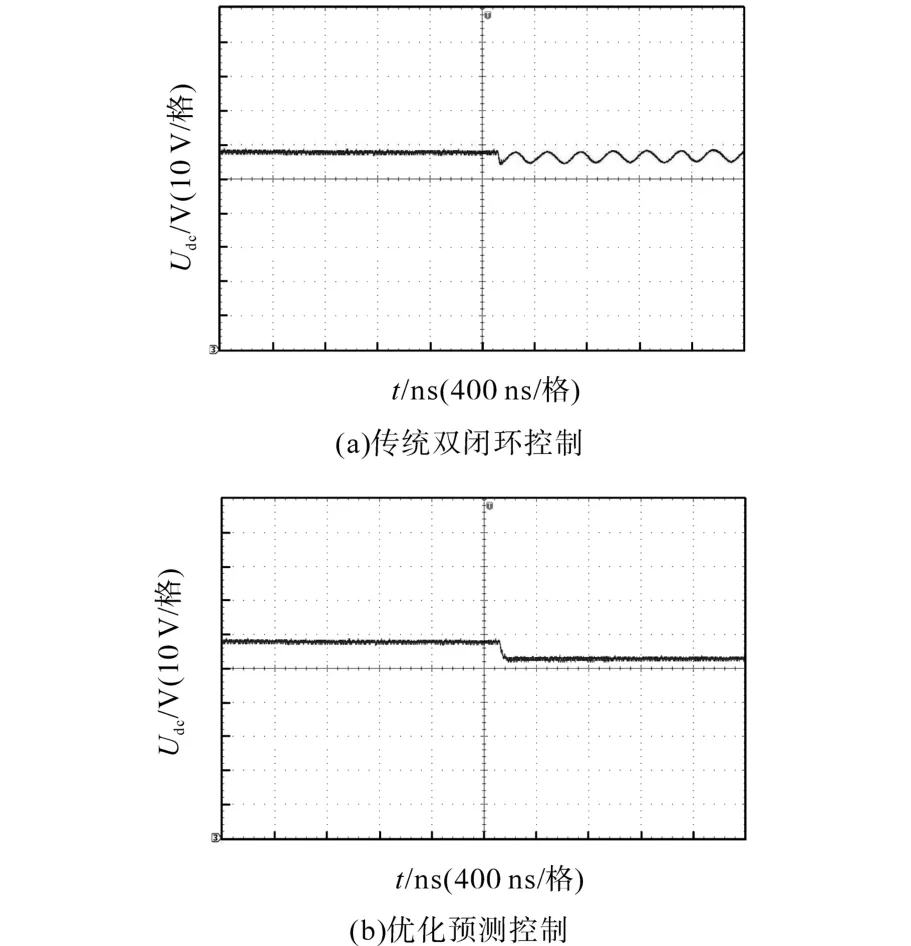
图10 网侧不平衡时直流侧输出电压实验波形Fig.10 Experimental waveforms of DC output voltage when the network side is unbalanced

5 结论

介绍了基于优化预测控制的VIENNA整流器设计方案。通过对主电路参数以及控制策略的分析与设计，建立基于Matlab/Simulink的仿真模型以及实验样机进行实验验证。仿真和实验表明，相对于传统的双闭环控制，优化预测控制具有较好的抗扰性、平稳性和动态性能。