基于扩张状态观测器的PMSM积分时变滑模控制

（青岛大学自动化学院，山东青岛266071）

永磁同步电机（permanent magnet synchronous motor，PMSM）由于其固有的低转子惯性、高效率、结构坚固、高功率密度等优点，在电动汽车、风力发电系统、机器人等各种工业应用中受到了广泛关注[1-3]。永磁同步电机的控制系统通常采用磁场定向结构，形成了内电流环和外速度环的串级控制结构。这项技术使得永磁同步电机具有与直流电动机相似的转矩控制性能，在转速和电流回路中采用比例积分控制，但电机参数的准确性会影响系统动态性能。此外，由于电动机的非线性、强耦合和振动特性[4-5]，传统的串级控制结构不能很好地处理机电方面的非线性问题。这些因素必然会影响控制系统的动态响应，在某些地方可能不能满足特殊要求[6-7]。

近年来，针对永磁同步电机驱动系统，各种采用现代控制技术的新型控制方法被提出，如自适应反步控制[8]、无源性控制[9]、滑模变结构控制[10]、模糊控制[11]、预测控制[12]、神经网络控制[13]等，均从不同方面提高了永磁同步电机的性能。在这些控制方法中，滑模变结构控制由于具有响应速度快、鲁棒性强、实现简单等优点[14-15]，因而受到学者们的广泛关注。在文献[16]中，针对PMSM的速度环控制，提出了一种基于新型趋近律的滑模控制方法，减小了抖振，同时设计了观测器来估计扰动，提高了鲁棒性。在文献[17]中，针对PMSM的电流环控制，设计了一种新的具有扰动补偿能力的滑模电流控制策略，改善了滑模控制过程的抖振现象，提高了电流的响应速度，实现了精确的电流跟踪控制。文献[18]应用分数阶微积分，设计了适用于永磁同步电机的分数阶滑模速度控制器，提高了永磁同步电机非线性速度控制的鲁棒性，并减少了抖振，同时提出了滑模负载转矩观测器，改进了控制器的性能。以上设计的控制器均采用串级控制结构，为了保证系统的稳定性而降低了系统的动态性能。

为了解决上述文献中存在的动态响应慢的问题，本文提出了一种新型积分时变滑模控制策略，将反馈线性化理论与积分时变滑模方法相结合，不同于传统的滑模控制，该积分时变滑模控制采用非线性滑模面，滑模面中的积分项可以有效地削弱传统滑模面带来的抖振，时变项加快了系统的动态响应速度。另外考虑到负载转矩等外界干扰，设计了扩张状态观测器，可实时估计负载转矩，提高系统的抗干扰性能。

1 永磁同步电机数学模型

对于隐极式永磁同步电机（Ld=Lq=L），在d-q同步旋转坐标系下的数学模型为[19-20]

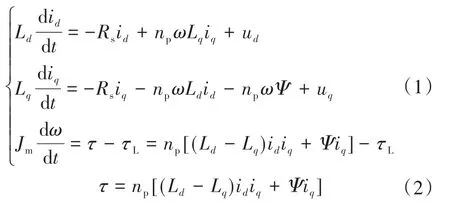
式中：ud，uq分别为d，q轴的定子电压；Ld，Lq分别为d，q轴的定子电感；id，iq分别为d，q轴的定子电流；Rs为定子电阻；np为极对数；Ψ为永磁体产生的磁链；Jm为转动惯量；τ为电磁转矩；τL为负载转矩；ω为转子机械角速度。

本文研究的永磁同步电机速度驱动系统的结构如图1所示。该控制系统包括逆变器、脉宽调制模块、永磁同步电机、坐标变换模块、单回路控制器和扩张状态观测器。为确保恒定的磁通工作状态，该系统采用基于的控制[21-22]。

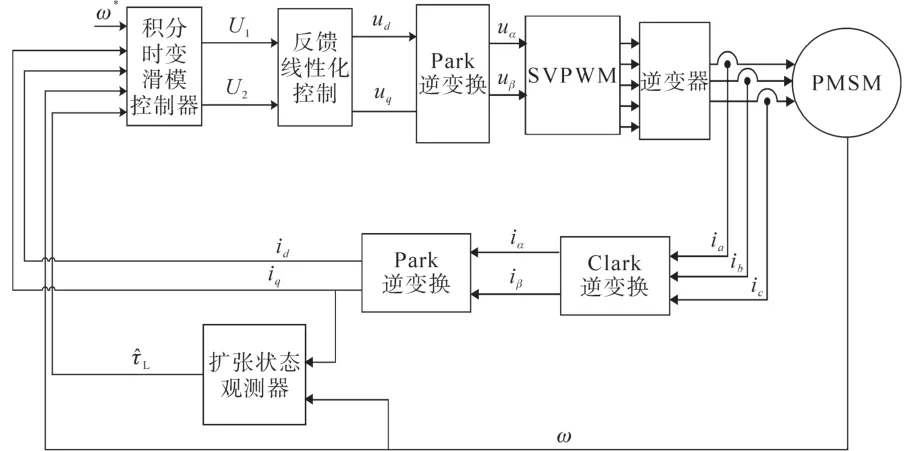
图1 PMSM速度控制系统框图Fig.1 The block diagram of PMSM speed control system

2 控制器的设计

为了实现永磁同步电机驱动系统的速度跟踪控制，使系统的动态响应更快，稳态性能更好，本文采用基于反馈线性化原理的积分时变滑模控制策略。

2.1 PMSM模型的线性化

式（1）所示的永磁同步电机的数学模型可被视为具有如下变量的非线性系统：

1）状态变量x=[x1x2x3]T=[idiqω]T；

2）输入变量u=[uduq]T；

3）输出变量y=[y1y2]T=[idω]T。

反馈线性化控制是实现系统动态解耦和全局线性化的有效方法，采用反馈线性化变换推导出完全解耦的永磁同步电机线性化模型。根据反馈线性化原理，在输入变量出现之前输出变量对时间的重复微分可推导为

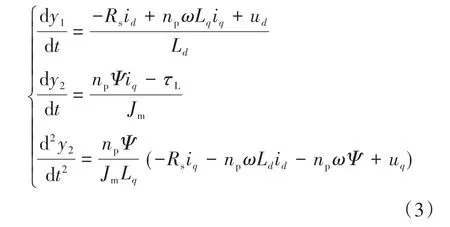
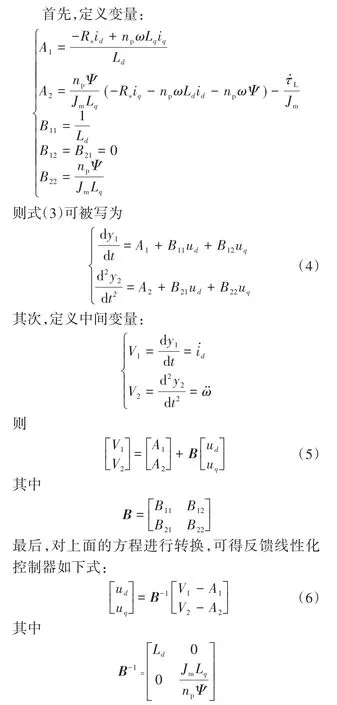
式（6）计算的控制律为基于反馈线性化的永磁同步电机控制系统的参考电压。然而，方程中包含中间变量，因此，本文引入积分时变滑模控制方法消除中间变量。

2.2 积分时变滑模控制器的设计

3 扩张状态观测器的设计

在实际的永磁同步电机伺服系统中，扰动是不可避免和不可检测的，例如负载转矩、参数不确定性等，特别是负载转矩，在整个系统跟踪控制精度中具有至关重要的影响。为了实时观测负载转矩，本文设计了一种新型的扩张状态观测器。

由于在实际运行过程中负载转矩是时变的，若采用此观测器实时观测负载转矩，则会快速抑制扰动，同时保证基于该观测器的速度控制器的有效性。

4 实验结果分析

基于Links-RT快速成型实验平台，对本文提出的基于扩张状态观测器的积分时变滑模控制策略的可行性进行了实验验证，该平台是由北京灵思创奇公司开发的一套半实物仿真系统，它可以实现与Matlab/Simulink的无缝连接。实验平台由研发型伺服驱动器、Links-RT仿真机、制动电阻、永磁同步电机和负载电机组成。永磁同步电机系统实验平台如图2所示。

图2 永磁同步电机系统实验平台Fig.2 Experimental platform of PMSM system

实验采用的是森创130MB150A型隐极式永磁同步电机，其参数为：转动惯量Jm=0.003 kg·m2，永磁体磁链Ψ=0.29 Wb，定子相电阻Rs=0.93 Ω，定子电感Ld=Lq=0.003 mH，磁极对数np=4。

为了验证所提控制策略的控制效果，本文共设计了2组实验。

实验1：在t=0 s时，给定转速ω=400 r/min，在t=10 s时，转速跳变到ω=700 r/min，在t=20 s时，转速跳变到ω=1000 r/min，分别进行电机空载启动和重载转矩变化条件下的实验。其中，重载转矩变化条件为：电机启动时转矩4N·m，在t=14s时，转矩变为8N·m，在t=18s时，转矩变为4N·m，得到PMSM驱动系统响应曲线，为了验证该控制算法的优越性，将其与传统滑模控制方法在速度跟踪性能上进行了比较。图3a为空载启动时的本文控制策略与滑模控制策略的速度响应对比曲线，图3b为重载转矩变化时的速度响应曲线；图4为本文所提控制策略在转速突变时的相电流响应曲线。

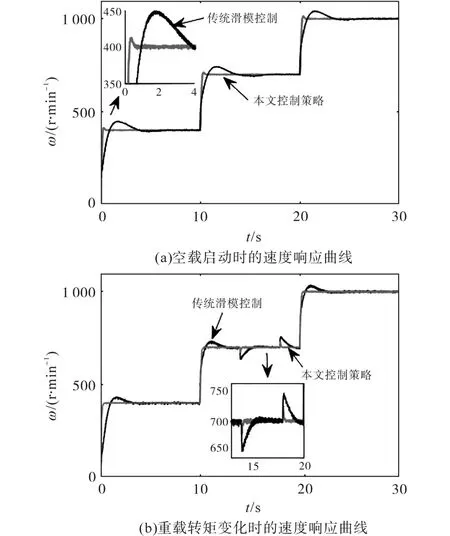
图3 转速变化时的速度响应曲线Fig.3 Speed response curves when speed varying

从图3的转速响应曲线中可以看出，本文所提控制策略的转速响应较之传统滑模控制算法要更快。如在转速ω=400r/min时，传统滑模控制的超调约为50 r/min，稳定时间约为4 s左右。本文所提控制策略基本无超调，稳定时间约为0.5 s。这表明本文所提控制策略使永磁同步电机驱动系统的速度响应更快且跟踪更平稳。

图4 转速变化时的三相电流响应曲线Fig.4 Three-phase current response curves when speed varying

实验2：系统空载启动，给定转速ω=1000 r/min，当电机进入稳态后，在t=10 s时突增负载转矩扰动τL=2 N·m，在t=15s时突减负载转矩扰动τL=2 N·m，得到系统响应曲线如下：图5为负载转矩变化下的本文所提控制策略与传统滑模控制算法的转速对比曲线；图6为本文所提控制策略在电机转速ω=1000 r/min时的三相电流曲线、d，q轴电流曲线和d，q轴电压曲线。

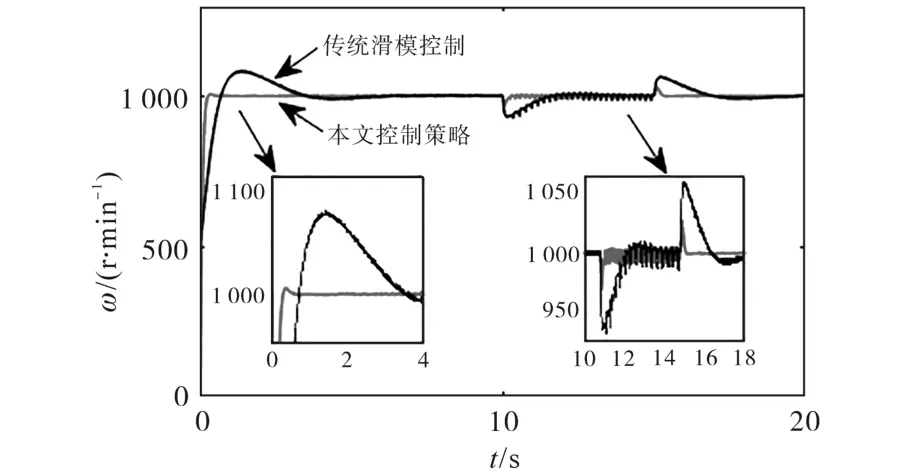
图5 负载变化时的转速响应曲线Fig.5 Speed response curves when load varying

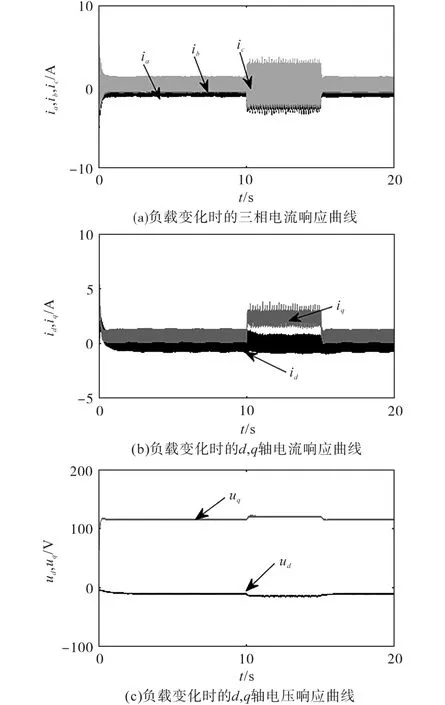
图6 负载变化时的电流和电压响应曲线Fig.6 Current and voltage response curves when load varying

从图5可以看出，当电机转速ω=1000 r/min时，本文所提控制策略的超调极小，稳定快，抖振小，传统滑模控制的超调约100 r/min左右，稳定时间长，抖振大。这表明本文所提控制策略的超调更小，稳定时间更短，系统响应速度更快、精度更高。当负载突变时，本文所提控制策略的波动为25 r/min，干扰恢复时间为0.3 s。传统滑模控制方法的波动约为60 r/min，波动较大，干扰恢复时间至少2 s左右。实验对比表明，在本文设计的控制策略下系统的转速变化很小，并且能很快恢复到给定转速，抖振幅度小。因此本文提出的基于反馈线性化的积分时变滑模控制策略不仅优化了系统的动态性能，而且增强了系统的鲁棒性。

从图6的电流和电压响应曲线中可以看出，本文所提控制策略不需要更高的电压来实现参考速度，另外，电压uq的波动较小，因此可知，本文所设计的控制策略相对于传统滑模控制，在一定程度上能够使系统更加快速地到达给定转速，有效提高了永磁同步电机驱动系统的动态性能。

由图5可知，在10～15 s之间负载发生变化，转速在经过微小的波动后能够迅速恢复到给定值，这表明本文设计的扩张状态观测器控制效果很好。图7为负载变化时的转矩观测值跟踪负载给定值的结果。由图7可知，本文所提出的观测器能够准确估计外部负载扰动，快速跟踪负载给定值，波动性较小，跟踪精度比较高。

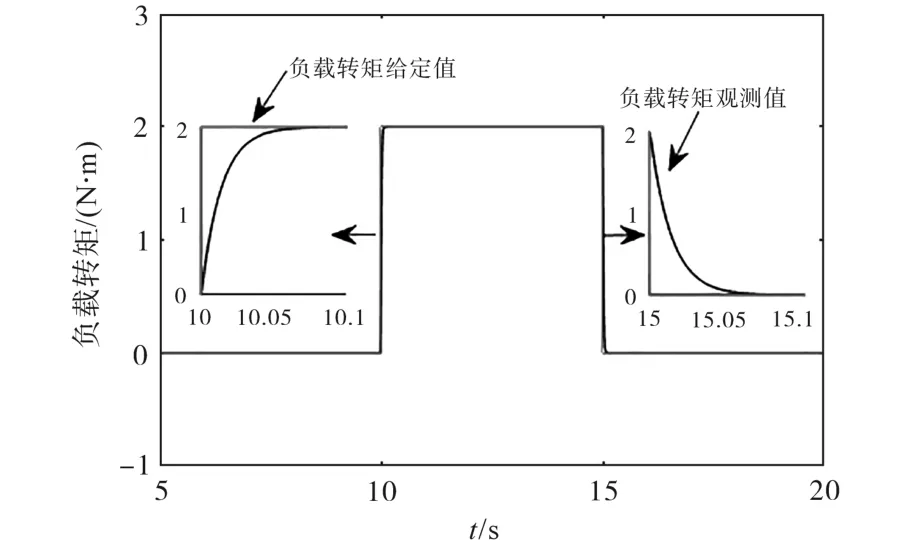
图7 负载变化时的负载转矩波形Fig.7 Load torque waves when load varying

基于以上实验研究可以看出，无论有无负载扰动，与传统滑模控制方法相比，本文提出的新型积分时变滑模控制器都能够快速无超调地响应给定转速，尤其当负载转矩突变时，本文提出的新型观测器能够快速跟踪并准确观测负载扰动，使得本文所提控制器能有效抑制负载变化对系统产生的影响，提高了系统的鲁棒性。因此，实验充分验证了本文提出的控制器与传统滑模控制相比更能够满足永磁同步电机驱动系统的高精度控制要求。

5 结论

1）围绕永磁同步电机驱动系统的速度控制问题，提出了积分时变滑模控制策略，该策略应用了反馈线性化理论，实验结果表明，相比于传统滑模控制，该策略可以保证系统动态响应速度更快、基本无超调。

2）该新型积分时变滑模控制策略对系统存在的扰动具有很好的鲁棒性，能够保证电机速度快速跟随给定且波动小，改善了系统的动态和稳态性能。

3）本文以负载转矩为扩张状态，设计了扩张状态观测器，能够较精确地实时观测负载转矩，提高了系统的抗扰性。