基于磁链与负载观测器的异步电机反步滑模控制

（青岛大学自动化学院，山东青岛266071）

异步电机（induction motor，IM）由于价格低廉、可靠耐用、维护要求低以及调速范围广的优点，被广泛用于工业制造中[1]。然而，异步电机是一个非线性、多变量和强耦合的系统，要想充分发挥其机械性能，需要选择合适的控制方法[2]。矢量控制使异步电机的磁通与转矩解耦，进而响应速度加快，调速性能也大幅提升[3-4]。实际工业生产中，电机的持续运行会导致绕组升温，这会使绕组参数发生摄动，其中转子电阻值会在很大程度上发生改变[5-6]，而且电机负载转矩通常是未知或不精确的，因此使矢量控制动态响应大打折扣，降低了系统运行的可靠性[7]。目前，有许多控制算法可以使异步电机系统具有良好的动、静态性能。文献[7]提出了一种暂态矢量估计器，将标量控制（v/f）的鲁棒性与矢量控制的动态性能融合在一起。文献[6]中使用已知回归模型来同时估计电机速度与定、转子电阻，增加了联合估计的稳定性。文献[8]设计了基于Gopinath模型的电压模型磁链观测器，其对转子电阻与互感变化具有鲁棒性。文献[9]利用模型参考自适应（model reference adaptive system，MARS）算法，在线辨识转子时间常数，降低了转子电阻摄动对转速的影响。文献[10]设计的模型预测控制结构简单，降低了参数调节的难度，但不能完全消除系统中的不确定因素和外部扰动。文献[11-12]设计了一种在零频或低频下的速度控制方法，提出一种新型自适应滑模观测器（sliding mode observer，SMO），对定转子电阻进行估计，增加了系统对参数不确定的鲁棒性和估计精度。哈密顿控制在电机参数变化时能够稳定跟随期望转速，但是系统的响应速度较慢[13]。模糊控制倚赖学者的经验，其应用范围也因此受到限制[14]。模型参考自适应与神经网络控制运算量大，对处理器性能要求较高，也没有被广泛应用于生产中[15-16]。滑模变结构控制鲁棒性好，但会使系统产生抖振，抖振过大会影响系统性能[17]。自适应反步控制可以减弱负载干扰的影响，但跟踪精度依赖于磁通的观测精度[18]。转子电阻摄动时，传统的开环磁链观测器不能准确估计出电机磁通值，常规滑模磁链观测器观测值抖振较大[19-20]。

本文设计了转子磁链观测器、负载转矩观测器与反步滑模控制算法，将转子磁通观测值用于负载转矩的估计，并将磁链与负载的观测值送入反步滑模控制器。实验结果表明，在转子电阻摄动与负载未知且变化时，该策略具有更好的运行性能。最后，针对电机启动或转速突变时定子电流与电磁转矩急剧增加的问题，提出了一种转速软给定策略，实验结果验证了该软给定方法的有效性。

1 异步电机数学模型

在d-q同步旋转坐标系下，按转子磁链定向λrd=λr,λrq=0，异步电机的数学模型为[19]

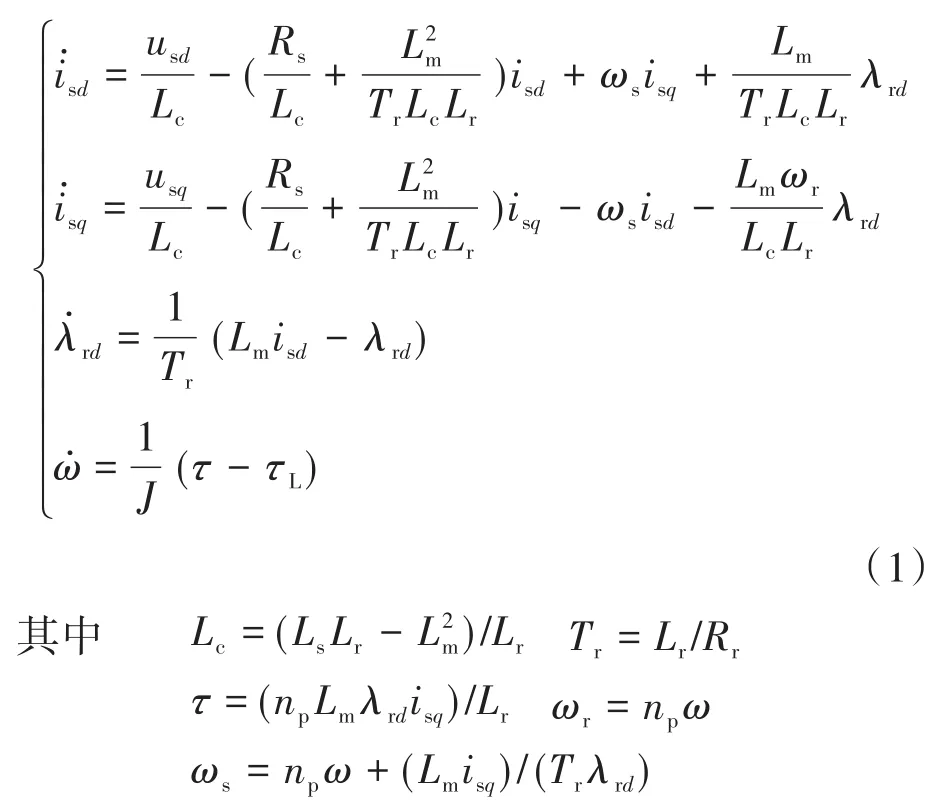
式中：Tr为转子时间常数；isd，isq分别为d，q轴的定子电流；usd，usq分别为d，q轴的定子电压；λrd，λrq分别为d，q轴的转子磁链；Rs，Rr分别为定子和转子电阻；Ls，Lr，Lm分别为定子电感、转子电感和定转子之间的互感；ω为转子机械角速度；ωs，ωr分别为定子电角速度和转子电角速度；J为转动惯量；np为极对数；τ，τL分别为电磁转矩和负载转矩。

2 异步电机控制系统框图

图1为异步电机反步滑模控制系统框图。观测器通过定子电流与转速的测量值，估计出磁通与负载，最后将测量值与观测值一起送入反步滑模控制器。

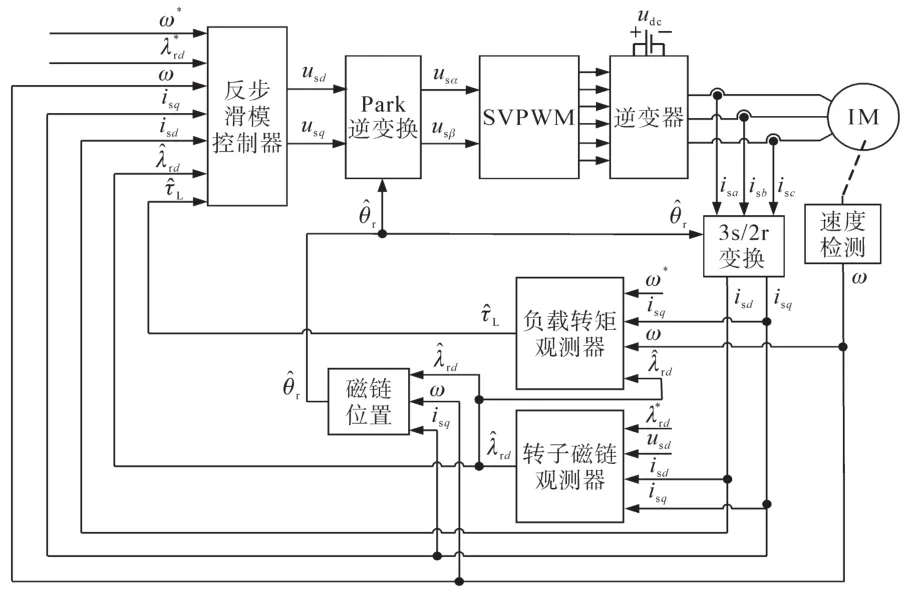
图1 异步电机反步滑模控制系统框图Fig.1 Structure diagram of backstepping sliding mode control of induction motor

3 转子磁链观测器设计

由于转子磁链λrd无法直接测得，根据式（1）所示的异步电机的数学模型，设计闭环指数趋近律的滑模转子磁链观测器。

观测器设计如下：

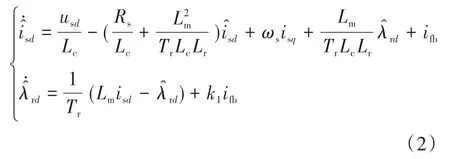
其中

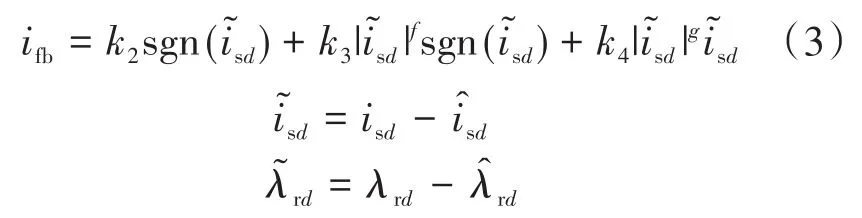
通过式（1）和式（2），可得定子电流与转子磁通的观测误差方程为

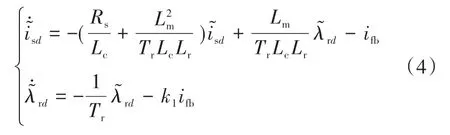
定义定子电流与转子磁通观测误差的滑模面为

定义Lyapunov函数为

根据式（3）～式（5），可得V1的一阶导数为

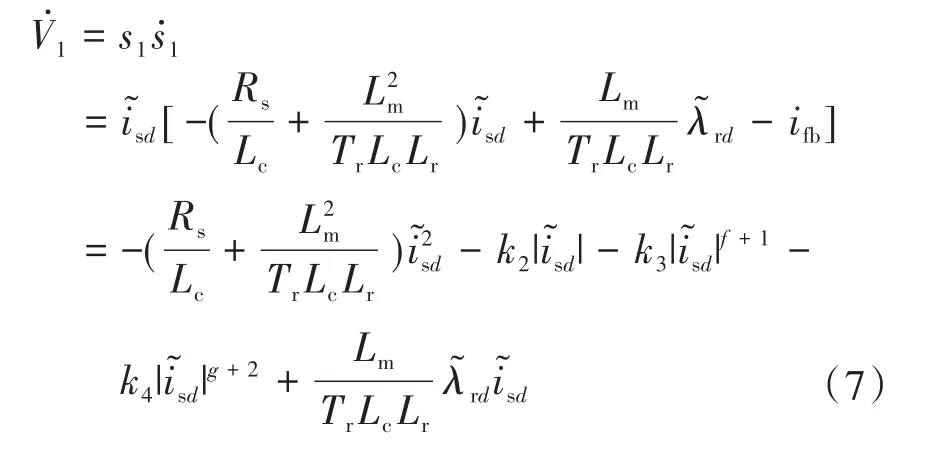
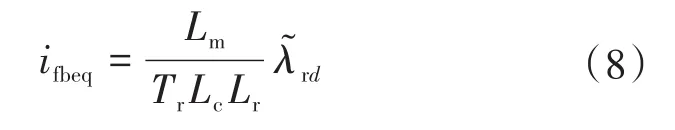
定义Lyapunov函数为

根据式（3）～式（5），可得V2的一阶导数为

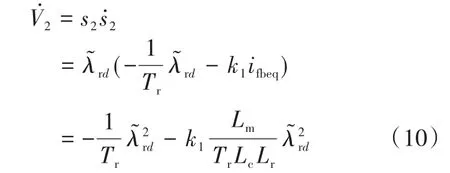
由于设计参数满足k1＞ 0，故可得。当且仅当，即s2=0 时，。根据 Lyapunov稳定性定理可知，d轴磁通是渐近收敛的。在控制律ifbeq的控制下，磁通观测值可以在有限时间内收敛至真实值λrd。

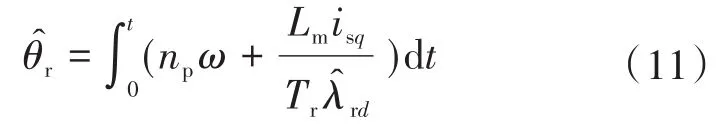
4 反步滑模控制器与负载转矩观测器的设计

4.1 反步控制器与负载转矩观测器设计

定义转速误差、磁链跟踪误差为

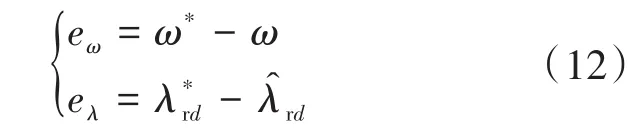
式中：ω*为给定的转子机械角速度为给定的转子d轴磁通。

根据式（1），可得式（12）的一阶导数为

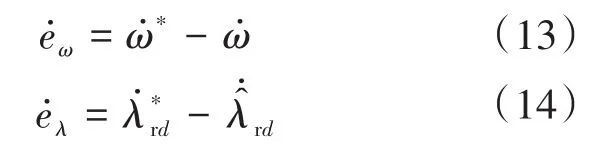
为了更好地抑制负载转矩扰动的影响，本文在反步控制器的设计步骤中，设计了负载转矩观测器，实现了对未知负载转矩的精确估计。定义Lyapunov函数为

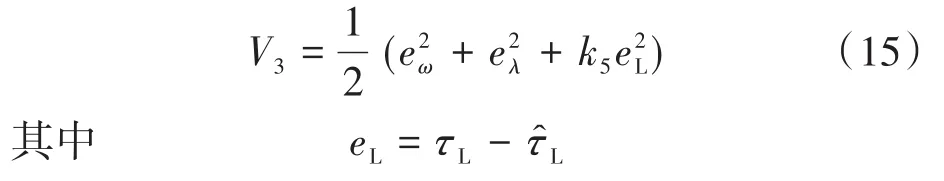
式中：k5为设计参数，k5＞ 0；eL，分别为负载转矩的误差值和估计值。

根据式（13）、式（14），可得V3一阶导数为

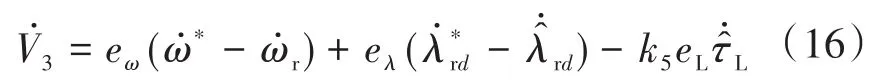
4.2 滑模控制器设计

5 系统稳定性分析

为了证明所设计控制器的稳定性，定义整个系统的Lyapunov函数为

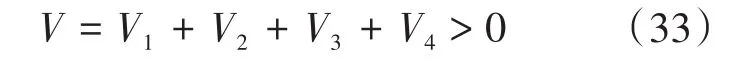
对式（33）求一阶导数，可得：

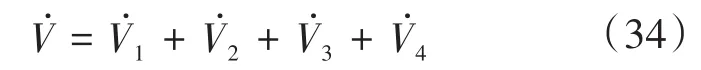
将式（7）、式（10）、式（19）和式（31）代入式（34），可得：

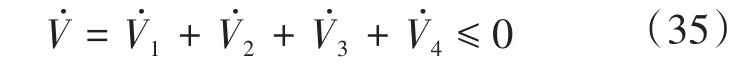
当且仅当s1=s2=s3=s4=eL=eλ=eω=0时。根据Lyapunov稳定性判据和Lasalle不变集可知，所设计的控制系统是全局渐近稳定的。

6 转速软给定

在电机启动或转速设定变化时刻，会产生较大的冲击电流，进而导致电磁转矩急剧升高，严重影响了电机系统的运行安全。因此，本文设计了一种转速软给定的方法，软给定转速为

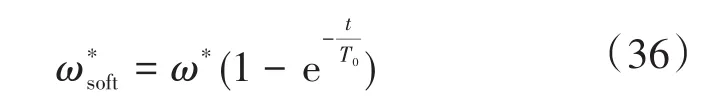
7 实验验证与结论

为了验证所设计控制策略的实用性，在基于LINKS-RT的感应电机变频调速实验平台上进行实验验证。LINKS-RT是北京灵思创奇公司开发的与Matlab/Simulink连接的变频调速系统。实验平台如图2所示，该平台由异步电机、负载电机、制动电阻、研发型伺服驱动器与仿真机组成。在给定转速变化、负载未知且变化和转子电阻摄动的情况下，将该控制策略与自适应反步控制方法进行实验结果的对比。磁链观测器参数为：k1＝0.00001，k2＝k3＝k4＝50，f＝g＝0.5；负载观测器参数为：k5=1100，k8=3 500；控制器参数为：k6＝k7＝50，k9＝k10＝1，k11＝k12＝k13＝k14＝1500，m=n=0.5；实验时间为20 s。实验采用的异步电机参数为：PN＝1.5 kW，UN＝220 V，IN＝5.9 A，nN＝1 500 r/min，Rs＝0.96 Ω，Rr＝0.93 Ω，Ls＝118.32 mH，Lr＝118.67 mH，Lm＝112.23 mH，τL＝9.6 N·m，np＝2，J＝0.0038 kg·m2。

图2 异步电机系统实验平台Fig.2 Experiment platform of induction motor system

为验证该控制策略对设定转速变化与负载未知且变化的鲁棒性，在t=0 s时，给定转速ω*=200 r/min，转子磁通，负载τL=1 N·m。5 s时，ω*增加至600 r/min，10 s时，ω*增加至1 000 r/min，15 s时，负载增加至2 N·m。响应曲线如图3所示。由图3可见，该策略在给定转速ω*变化时，有更快的响应速度；稳态时该策略的跟踪精度更高；负载转矩未知且变化时，该控制策略能准确快速地估计出实际负载转矩，且在负载转矩变化时刻，电机转速波动更小；改进型滑模磁链观测器能准确地观测到电机转子磁链，且较常规滑模观测器的抖振更小。

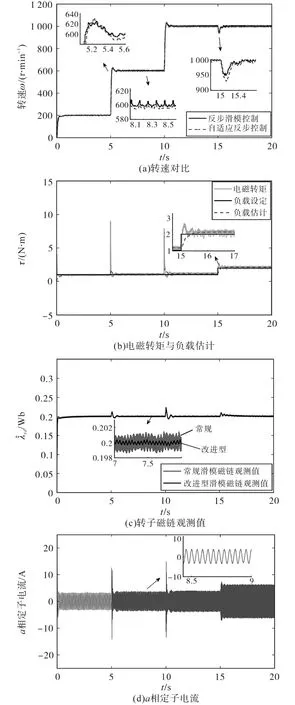
图3 转速与负载转矩变化时的实验曲线Fig.3 Experimental curves when the speed and load torque change

实验中异步电机转子电阻无法突变，可更改控制器中转子电阻的参数Rr来模拟电机转子电阻突变。为验证该控制策略对转子电阻摄动的鲁棒性，在图3的实验条件下，t=8 s时将控制器中的参数Rr变为标称值的0.5倍，即Rr=0.465 Ω。实验响应曲线如图4所示。由图4可见，转子电阻突变后，该策略转速波动小且能迅速跟踪至给定转速；所设计的磁链观测器仍能准确观测到转子磁链，且较常规滑模观测器的抖振小。

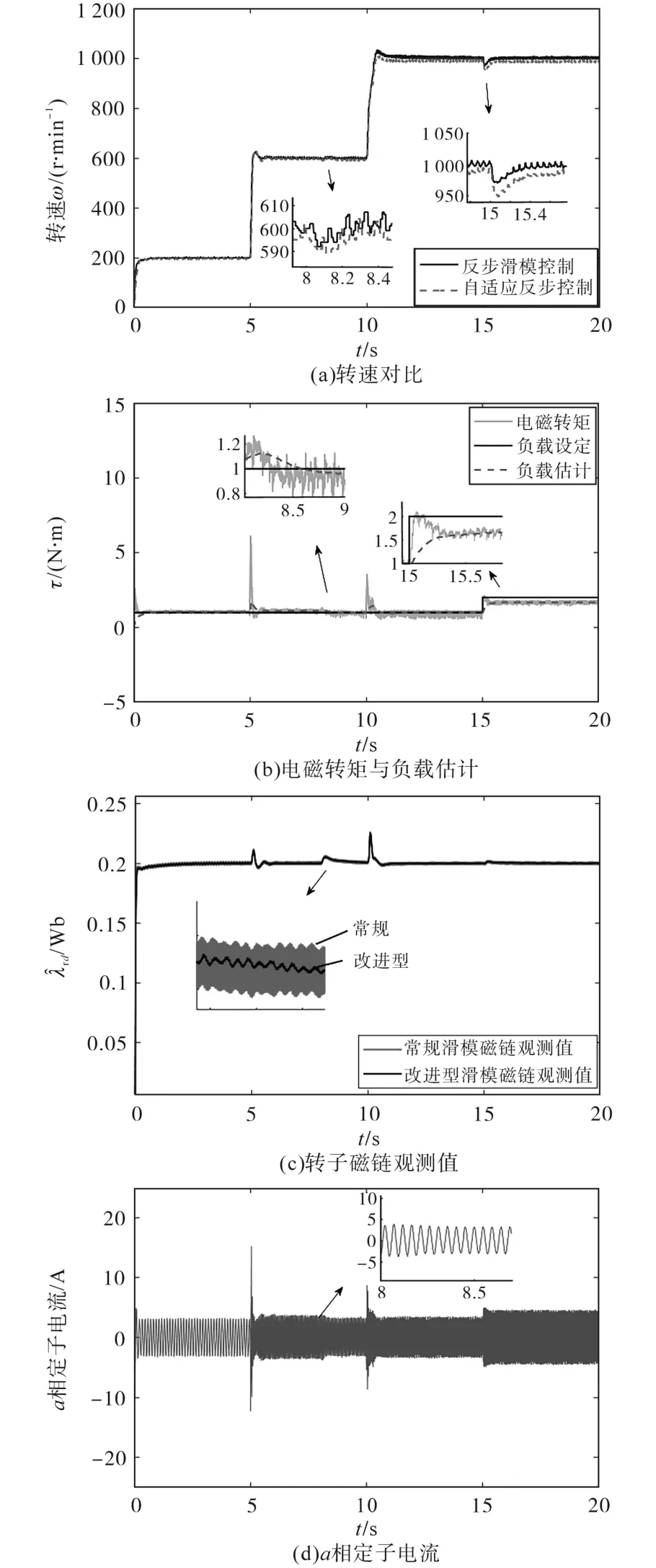
图4 转子电阻摄动时的实验曲线Fig.4 Experimental curves when the rotor resistance perturbation

在图3的实验中，电机启动或给定转速变化时刻，定子电流与电磁转矩急剧增加，这会影响电机系统的寿命与运行安全。采用本文设计的转速软给定的方法，将给定转速ω*通过式（36）转换为软给定转速，其中设计参数T0=0.2。再次运行图3条件下的电机系统，响应曲线如图5所示，软给定前后数据对比如表1所示。由图3、图5与表1可见，在转速软给定条件下，该控制策略在转速变化的时刻（0 s，5 s，10 s），定子电流与电磁转矩的峰值明显减小，验证了转速软给定算法的实用性，增强了电机系统的使用安全。

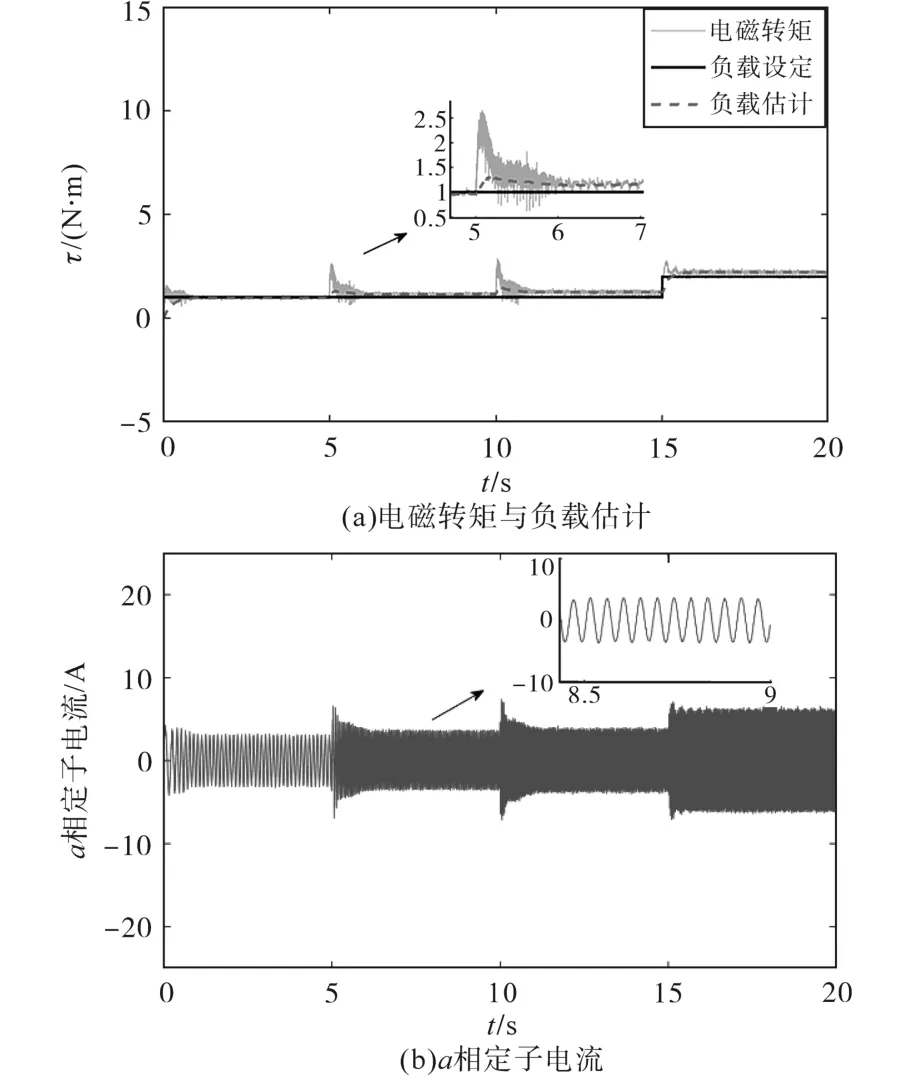
图5 转速软给定下的实验曲线Fig.5 Experimental curves when the soft speed setting

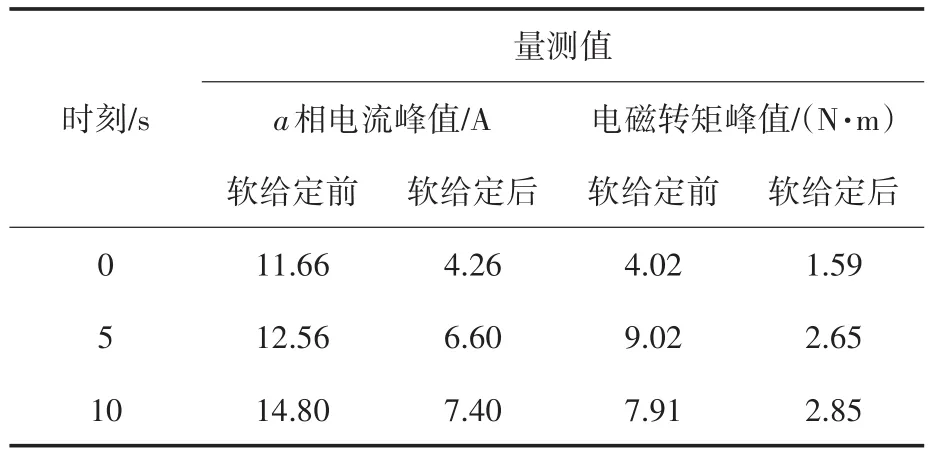
表1 转速软给定下的数据对比Tab.1 Data comparison of the soft speed setting

本文设计了改进型磁链观测器、负载转矩观测器与反步滑模控制策略，提出了一种转速软给定算法。利用电流和转速的测量值，精确估计出转子磁通值，同时将磁通观测值用于负载转矩估计。实验结果表明，所设计的观测器可以准确观测出磁通与负载转矩，设计的控制策略响应速度快且稳态精度高，有效抑制了转子电阻摄动与负载扰动对系统性能的影响，使异步电机速度控制具有良好的鲁棒性、动态响应速度与跟踪精度。最后，实验结果验证了转速软给定方法的有效性。