湍流情况下气溶胶微小通道沉积规律数值模拟研究
涂 卓,曹学武
湍流情况下气溶胶微小通道沉积规律数值模拟研究
涂 卓,曹学武*
(上海交通大学,上海 200240)
本文利用数值模拟方法研究湍流情况下气溶胶微小通道内的沉积规律。通过对Muyshondt实验的模拟并与实验数据对比验证了雷诺应力模型(RSM)和离散相模型(DPM)的适用性。分析了颗粒粒径、气体流量对气溶胶沉积的影响,并利用修正后的DPM模型研究了通道弯曲度对气溶胶沉积的影响。结果表明在湍流情况下,气溶胶在微通道内沉积占优机制为湍流扩散,主要影响粒径较小的气溶胶颗粒,随着雷诺数增大,湍流扩散增强,颗粒总沉积率增大;在弯曲通道内,气溶胶颗粒沉积率随粒径变化呈现先增大后减小的趋势,由于惯性碰撞作用增强,颗粒总沉积率相比水平通道显著增大,但进一步增大通道弯曲度对颗粒总体沉积率的影响不显著。
气溶胶;湍流;微通道
当反应堆发生严重事故时,安全壳内会弥散大量放射性气溶胶,气溶胶可通过安全壳上的微小缝隙泄漏进入环境中。已有研究表明,微小通道对气溶胶颗粒具有显著的去除作用。因此,研究气溶胶在微小通道内的沉积对事故后放射性源项的确定具有重要意义。
气溶胶在微小通道内沉积现象十分复杂,通常情况下,安全壳内放射性气溶胶颗粒粒径较小,安全壳内混合气体流动对气溶胶颗粒在微小通道内的沉积有显著影响。加拿大英属哥伦比亚大学Bowen[1]等提出层流条件下气溶胶微粒在矩形或者圆通道中沉积的计算模型,模型过于简单,计算结果与实验结果相比存在量级上的差异。Nazaroff[2]研究了层流条件下气溶胶在微小通道内的沉积,模型考虑了布朗扩散、重力沉降和惯性碰撞三种主要的颗粒沉积机制,并假设这些机制是独立的,总穿透率为三个独立过程穿透率的乘积,该模型在低雷诺数下与实验结果具有较好符合性。印度原子能监管委员会的Bishnoi[3]等利用Realizable-湍流模型和DPM模型研究层流流动下气溶胶在混凝土随机裂缝中的沉积,模拟结果与实验结果具有较好的符合性,该文未进一步研究湍流流动对气溶胶沉积的影响。
在严重事故条件下,微小通道两端具有较大压差,气体在通道内形成湍流。湍流扩散作为一种新的沉积机制引入。目前对该机制的机理模型研究较少,大多为基于实验数据提出的经验模型。Liu和Agarwal[4]提出了基于无量纲松弛时间和无量纲沉积速率的经验关系式。Sippola与Nazaroff[5]试图将机理模型与经验关系式结合起来,并将施密特数引入模型,认为对于大多数反应堆事故分析经验模型都是适用的。韩云龙[6]等利用雷诺应力湍流模型和DPM模型研究厘米级通风管道内颗粒物的沉积,模拟结果基本符合实验数据和经验关系式。Tian[7]研究了不同湍流模型和壁面模型对计算结果的影响,认为雷诺应力湍流模型及二层边界条件的使用能合理的预测颗粒物的沉积。
本文利用Fluent中的机理模型分析湍流流动下毫米级微小通道内气溶胶沉积现象。研究粒径和载气流量对气溶胶颗粒沉积的影响。针对气溶胶在弯曲通道内的沉积利用UDF对原DPM模型进行修正,并进一步研究气溶胶在弯曲通道内的沉积规律。
1 模型及模型验证
颗粒的运动由DPM模型计算,颗粒运动方程为公式(1),主要考虑流体对颗粒的曳力和颗粒重力,计算颗粒运动轨迹,当颗粒运动至出口,认为其逃逸,当颗粒运动至壁面,认为其沉积。
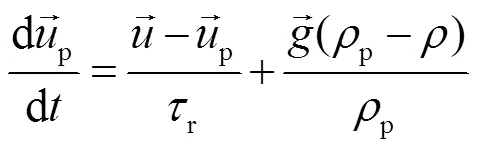


该模型有以下假设:
(1)气溶胶固体项为稀相,忽略颗粒间碰撞。
(2)单项耦合,仅考虑气体对颗粒的作用。
(3)忽略气溶胶颗粒与壁面的碰撞反弹。




——平均轴向气流速度;
——管道长度;
——气溶胶颗粒穿透率;
——摩擦因子。
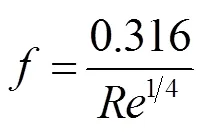



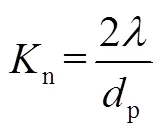
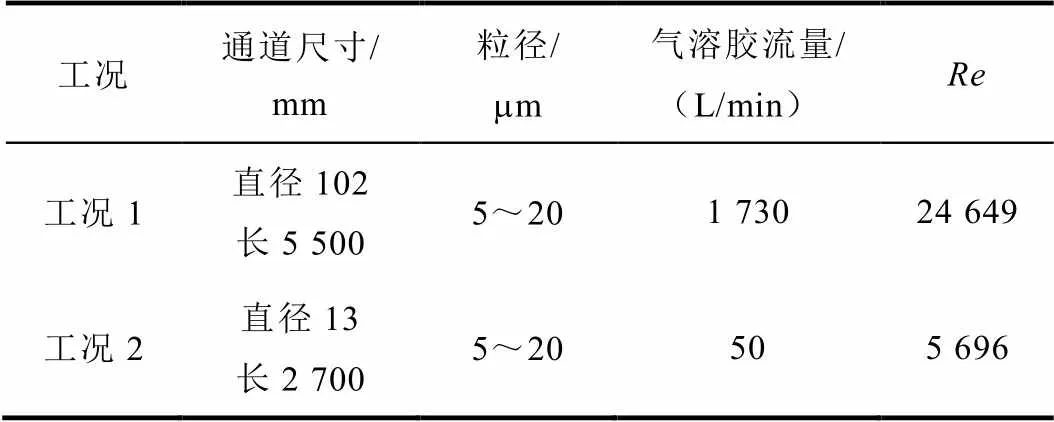
表1 实验参数表
考虑到管道为规则对称几何,故将计算域简化为二维模型,网格参数如表2所示,满足模型计算要求。
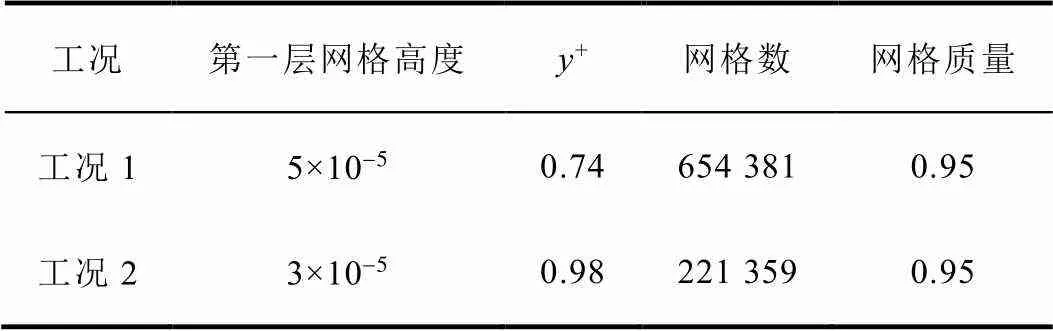
表2 网格参数
计算假定入口颗粒粒径满足Rosin-Rammler[10]分布。
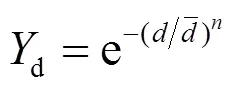
——分布参数。
模拟结果与实验数据对比如图1所示。本文分别选用Realizable-湍流模型和雷诺应力湍流模型对流场进行模拟,从对比结果看,选用雷诺应力湍流模型时,模拟结果与实验吻合更好,由于雷诺应力模型考虑了湍流流场的各向异性,可以得到更精确的湍流流场,使得DPM模型可以更加准确计算颗粒的轨迹因此模拟得到无量纲沉积速率随无量纲松弛时间变化趋势与实验结果基本吻合,并且误差保持在一个量级以内,说明用雷诺应力湍流模型与DPM模型耦合的方法分析通道内气溶胶沉积是合理的。
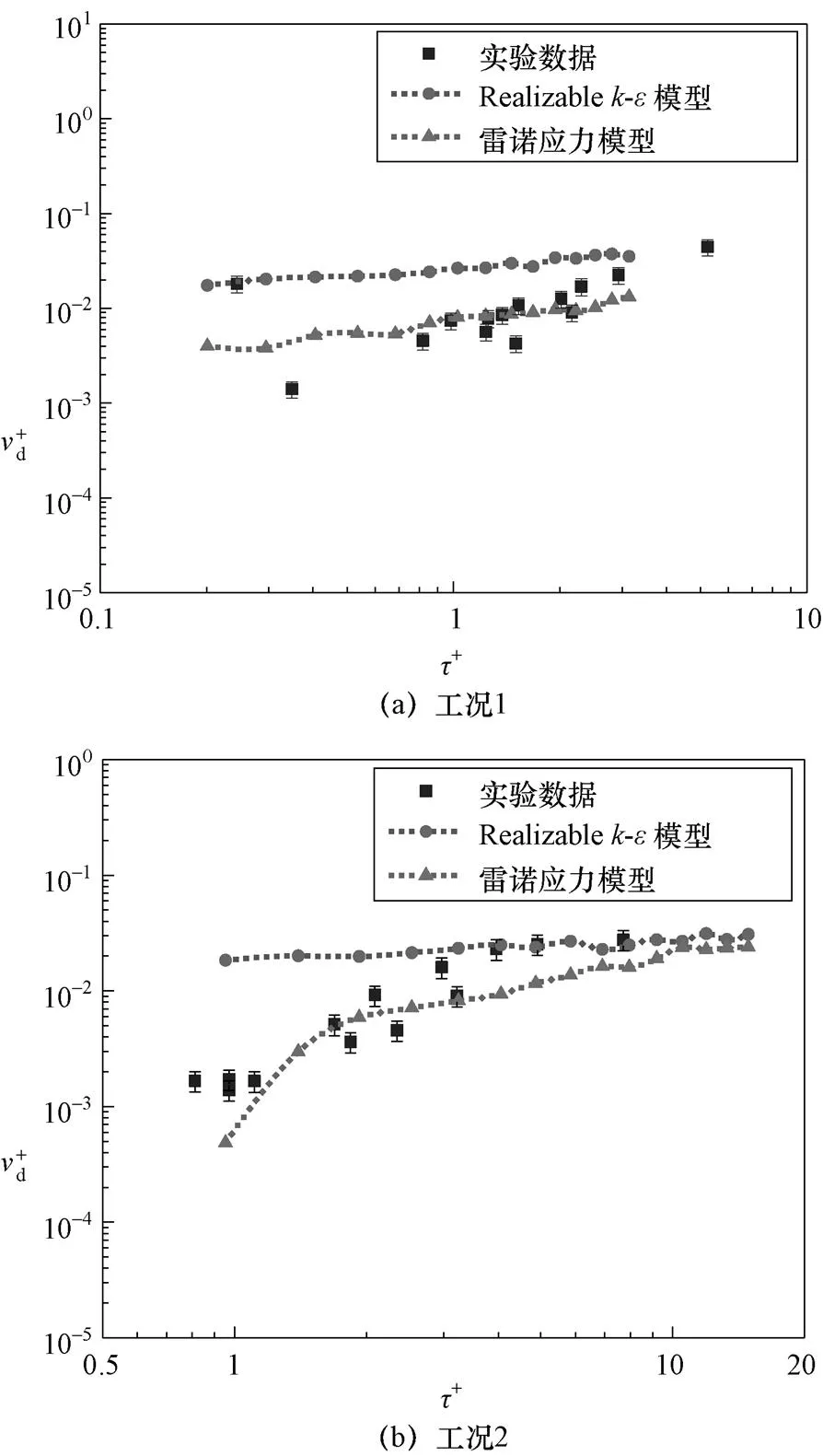
图1 模拟结果与实验数据对比
2 结果与讨论
建立毫米级微通道模型,通道直径1 mm,长52 mm,如图2所示。研究颗粒粒径、气溶胶流量和通道弯曲度对颗粒沉积的影响,分析湍流情况下不同沉积机制的作用规律。

图2 微通道几何模型
2.1 颗粒粒径对沉积的影响
选取二氧化钛颗粒进行研究,颗粒粒径为0.5~5 μm,浓度200 mg/m3。得到湍流流动时颗粒沉积率(沉积率定义为颗粒沉积量与总量比值)随粒径变化曲线,如图3(b)所示。可以看出,颗粒粒径对沉积率有明显影响。当载气流动为湍流时,整体上看沉积率变化曲线呈现增长趋势,即气溶胶颗粒沉积率与颗粒粒径正相关。但可根据局部变化情况将曲线大致分为三个不同的区域,即稳定区、增长区和波动区,根据方程(1),在不考虑其他作用力的情况下,颗粒受重力和流体曳力是影响颗粒运动轨迹的主要因素,随着粒径的增大,重力沉降作用更加显著,导致大颗粒更容易在通道内沉积。随着粒径增大,沉积率变化不再明显,该现象的出现是由于随着颗粒粒径逐步增大,颗粒具有更大惯性,使得湍流扩散的影响逐步减弱。
2.2 气溶胶载气流量对沉积的影响
选取不同气溶胶载气流量,计算得到沉积率随粒径变化曲线如图3所示,当层流流动时,随着雷诺数增大,气溶胶沉积率呈现下降趋势;当湍流流动时,随着雷诺数增大,气溶胶沉积率呈现上升趋势,表明在湍流情况下,气溶胶沉积占优机制与层流情况下不同,湍流扩散使得颗粒运动轨迹偏离流线,增加了颗粒与壁面惯性碰撞的概率,使得颗粒沉积率增大。
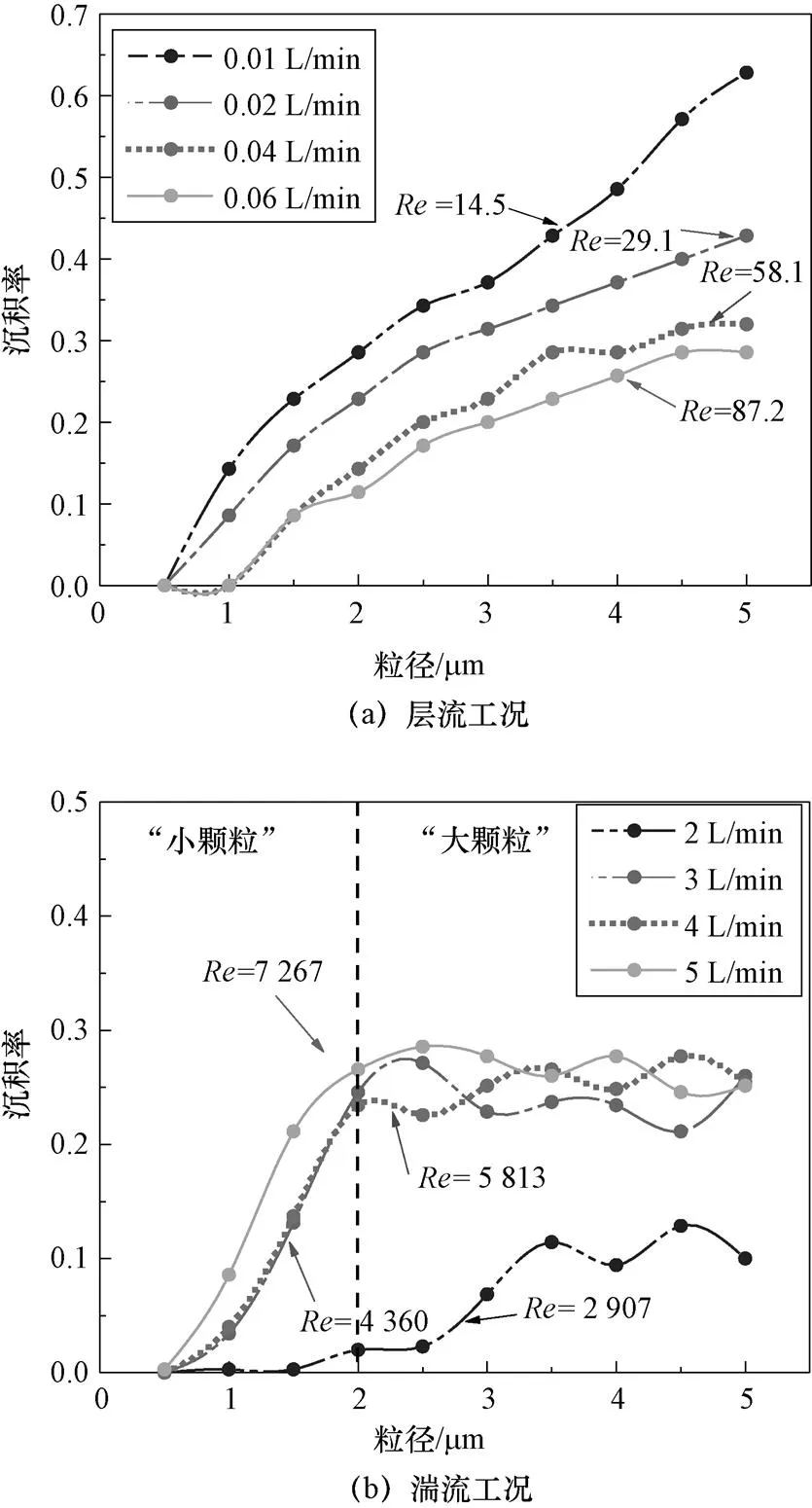
图3 不同流量下沉积率随粒径变化
根据沉积率的变化趋势将颗粒划分为“小颗粒”(0.5~1.5 μm)和“大颗粒”(2~5 μm)。随着雷诺数由2 907进一步增大,小颗粒的沉积率继续增大,而大颗粒的沉积率变化不明显。分别统计小颗粒和大颗粒在不同流量下的总体沉积率得到图4所示柱状图。可知随着雷诺数进一步增大,小颗粒总体沉积率从5.5%增加到10%,大颗粒沉积率由24%增加到26%。说明湍流扩散可以显著提高小颗粒的沉积率。主要原因为大颗粒具有更大的惯性,能够在一定程度上削弱湍流扩散的影响。
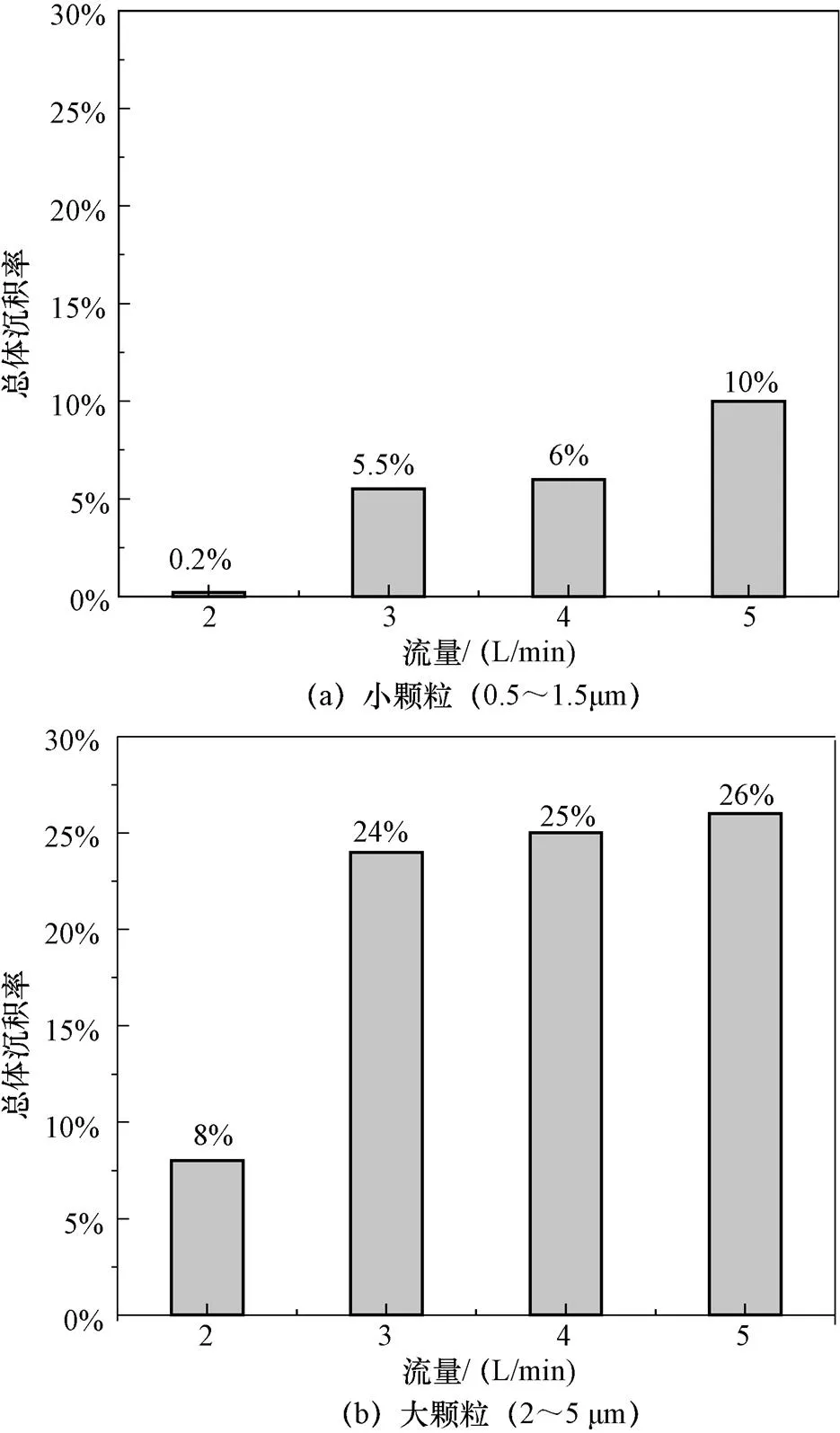
图4 颗粒总体沉积率统计图
图5给出了通道上下壁面颗粒质量浓度分布曲线,随着湍流的增强,颗粒单位距离的沉积量增大,并且通道上下壁面颗粒浓度分布趋于一致,上壁面浓度甚至略高于下壁面。表明湍流状态时,湍流扩散的影响会高于重力沉降成为占优机制。

图5 通道上下壁面颗粒浓度分布

图5 通道上下壁面颗粒浓度分布(续)
2.3 弯曲通道内沉积模型的修正与弯曲度影响分析
本节建立四种不同弯曲度的通道几何模型,如图6。通道长均为52 mm,弯曲度分别为0°、30°、60°、90°,气溶胶流量为5 L/min。

图6 通道几何模型
考虑到在弯曲通道内惯性碰撞将成为气溶胶沉积的占优机制,原模型中颗粒接触壁面就沉积的假设不再适用于气溶胶颗粒在弯曲微小通道内的沉积,因此必须采用新的模型考虑颗粒与壁面的碰撞,同时引入新的沉积判定准则来对原模型做出修正。
(1)气溶胶沉积判定准则
Konstandopoulos[11]等在研究中,引入了“临界碰撞角”的概念并检验了该准则的有效性。碰撞角定义如下:
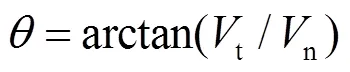
该模型中,颗粒的沉积判定依据基于临界碰撞角,即当颗粒入射角超过临界碰撞角时,认为颗粒沉积,否则反弹。颗粒沉积判定准则为:

模型采用能量分析法对斜向碰撞进行评估,得到临界碰撞角为:
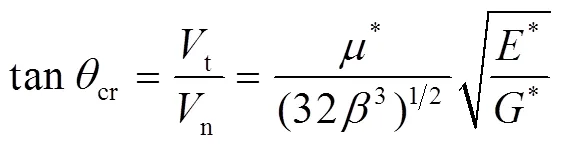
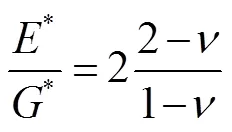
(2)颗粒碰撞反弹速度计算
清华大学施学贵等[12]利用多脉冲全息激光技术研究气溶胶颗粒在气流中的运行,通过大量统计研究发现颗粒与壁面碰撞恢复系数与入射角度和入射速率有关,得到如下经验关系式:

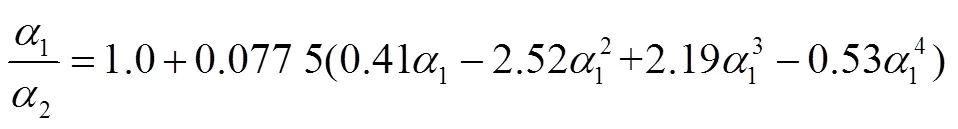
颗粒与壁面碰撞示意图如图8所示。
图8 颗粒与壁面碰撞示意图
Fig.8 The schematic of particle collision with wall
基于上述模型,通过用户自定义函数(UDF)对壁面边界条件进行修正,并将其动态链接到 Fluent求解器中与DPM模型进行耦合,使Fluent在计算气溶胶颗粒运动轨迹时考虑颗粒与壁面的碰撞反弹,并根据新的颗粒沉积判定准则统计颗粒的沉积率。数值模拟过程如图 9所示。
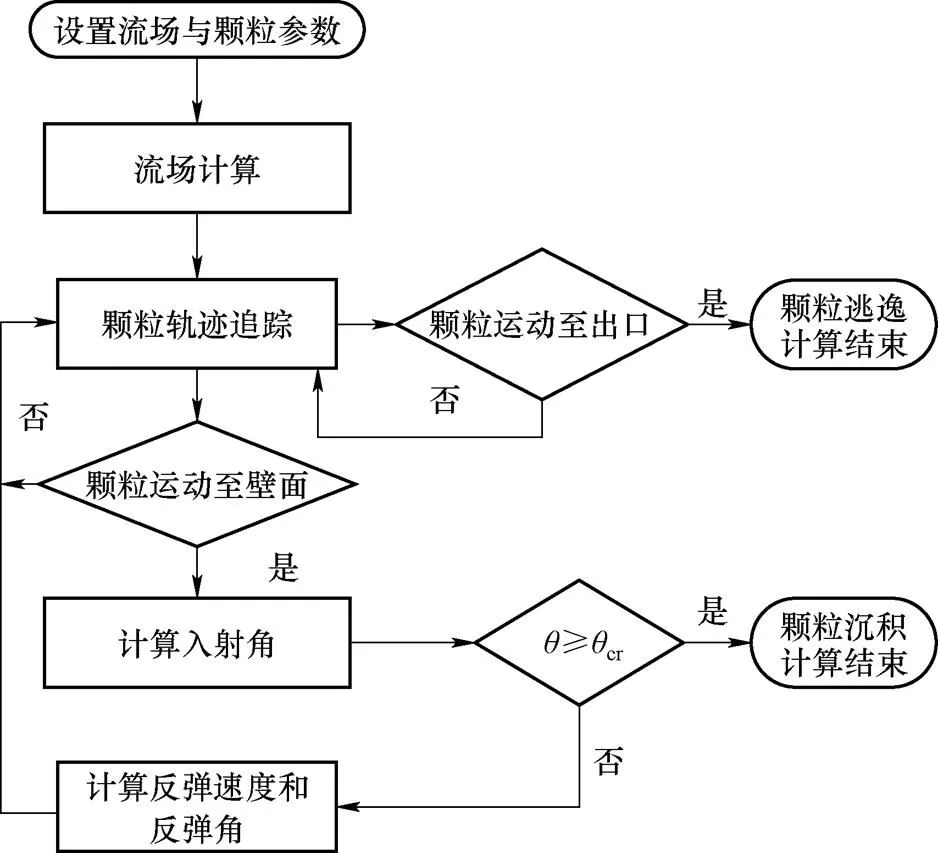
图9 修正模型计算流程图
采用修正后的DPM模型计算弯曲通道内气溶胶的沉积率,并与原模型进行对比,如图 10所示。结果显示,在直管中修正后模型与原模型计算结果基本一致,表明原模型计算直管中气溶胶颗粒沉积是适用的。在弯管计算中,修正后模型与原模型计算大颗粒的沉积率有很大差异。原模型中,粒径较大的颗粒由于碰撞频率较大,在不考虑颗粒反弹的情况下几乎全部沉积。修正模型计算结果中小颗粒由于具有较小的斯托克斯数,具有很好的随流性,使得小颗粒极容易跟随流体从出口逃逸;随着粒径增大,颗粒碰撞概率显著增大,由于与壁面碰撞反弹,颗粒并不会全部沉积。大颗粒随流性差导致其轨迹偏离流线,故与壁面碰撞时能够有较大的碰撞角,导致其不容易沉积,因此随着粒径增大,大颗粒沉积率呈现下降趋势。
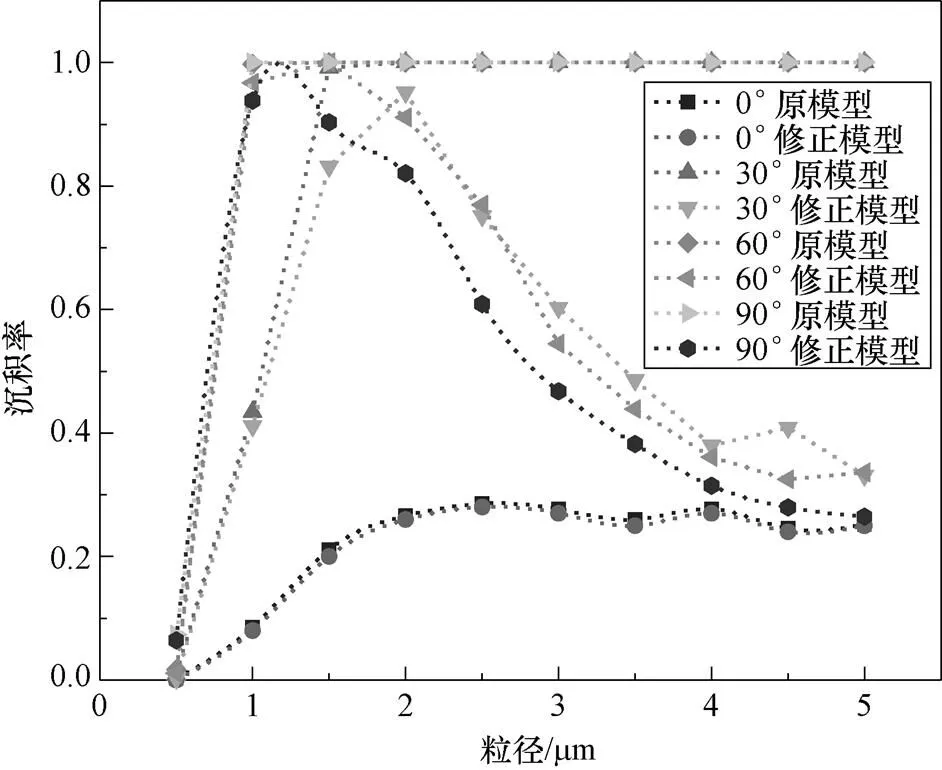
图10 修正DPM模型计算结果与原模型对比
图11给出利用修正模型计算得到的颗粒总体沉积率随弯曲度变化统计图,可以看出气溶胶颗粒在弯曲管道内的沉积率明显高于直管,说明弯曲管道可以显著提高气溶胶颗粒的惯性碰撞,促进气溶胶颗粒的沉积,但弯曲度进一步增大对沉积率的影响十分有限,甚至可能导致颗粒沉积率略微出现下降。由90°弯管壁面沉积颗粒质量浓度云图(见图12)可知,气溶胶在弯曲微小通道内的沉积主要集中于弯管段入口处,在弯管段后半部由于持续的惯性碰撞出现离散的沉积点,管道上壁面颗粒沉积极少,可知在弯曲通道内气溶胶沉积主要机制为惯性碰撞。

图11 颗粒总体沉积率随弯曲度变化统计图

图12 90°弯管壁面沉积颗粒质量浓度云图
3 结论
(1)本文利用雷诺应力模型和DPM模型对Muyshond实验进行模拟,并与实验数据对比,验证了该模型分析湍流情况下气溶胶在微小通道内沉积现象的适用性。
(2)气溶胶颗粒粒径和气溶胶载气流量均对气溶胶颗粒沉积具有显著影响,湍流情况下随着颗粒粒径的增大,颗粒沉积率先增大后趋于稳定;随着载气流量增大,气溶胶沉积率呈现增大的趋势。
(3)在湍流情况下,气溶胶在微小通道内的主要沉积机制为湍流扩散,湍流扩散主要影响粒径较小的气溶胶颗粒,增大气体雷诺数可以增强湍流扩散的影响,使得气溶胶颗粒在壁面的沉积趋于均匀。
(4)在弯曲通道内,气溶胶颗粒沉积率随粒径变化呈现先增大后减小的趋势,弯曲通道相比水平通道可以显著增强气溶胶颗粒的惯性碰撞,促进气溶胶颗粒的沉积,在弯曲通道内气溶胶沉积主要机制为惯性碰撞。
[1] Bowen B D,Levine S,Epstein N.Fine particle deposition in laminar flow through parallel-plate and cylindrical channels[J].Journal of Colloid and Interface Science,1976,54(3):375-390.
[2] Liu D L,Nazaroff W W.Modeling pollutant penetration across building envelopes[J].Atmospheric Environment,2001,35(26):4451-4462.
[3] Bishnoi L R,Vedula R P.Prediction of air leakage and aerosol transport through concrete cracks with a fractal based crack morphology model[J].Nuclear Engineering and Design,2013,265:393-401.
[4] Liu B Y H,Agarwal J K.Experimental observation of aerosol deposition in turbulent flow[J].Aerosol Science,1974,5:145-155.
[5] Sippola M R,Nazaroff W W.Particle deposition from turbulent flow:review of published research and its applicability to ventilation ducts in commercial buildings[R].Lawrence Berkeley National Laboratory,2002.
[6] 韩云龙,胡永梅,钱付平.通风管道内温湿度对颗粒沉积的影响[J].土木建筑与环境工程,2010,32(4):66-70.
[7] Tian L,Ahmadi G.Particle deposition in turbulent duct flows-Comparisons of different model predictions[J]. Journal of Aerosol Science,2007,38(4):377-397.
[8] Gosman A D,Ioannides E.Aspects of computer simulation of liquid-fuelled combustors[J].Energy,1983,7(6):482–490.
[9] Muyshondt,Arnold,Anand N K,et alTurbulent deposition of aerosol particles in large transport tubes[J].Aerosol Science and Technology,1996,24(2):107-116.
[10] ANSYS,Inc.ANSYS Fluent Theory 2019R3[R].201 9.
[11] Konstandopoulos,Athanasios G.Particle sticking/rebound criteria at oblique impact[J].Journal of Aerosol Science,2006,37(3):292-305.
[12] 施学贵,徐旭常,冯俊凯.颗粒在湍流气流中运动的受力分析[J].工程热物理学报,1989,10(3):320-325.
Simulation of Aerosol Deposition in the Micro-channel under Turbulent Flow
Tu Zhuo,Cao Xuewu*
(Shanghai Jiaotong University,Shanghai 200240,China)
In this paper, the numerical simulation method is used to study the deposition law in the aerosol micro-channel under turbulent flow. The applicability of the Reynolds Stress Model (RSM) and the Discrete Phase Model (DPM) is verified by the experimental results of the Muyshondt experiment. The influence of the particle size and the gas flow rate on aerosol deposition is analyzed using the original DPM model, while the influence of the channel curvature on the aerosol deposition is studied using the modified DPM model with UDF considering the collision. The results show that in the case of turbulent flow, the dominant mechanism of the aerosol deposition in the microchannel is turbulent diffusion. Turbulent diffusion mainly affects aerosol particles with smaller diameters. As the Reynolds number increases, turbulent diffusion increases, the overall particle deposition rate increases. In the curved channel, the deposition rate of aerosol particles first increases and then decreases with the change of the particle size. Due to the enhanced inertial collision effect, the overall particle deposition rate increases significantly compared with the horizontal channel. But further increasing the channel curvature has no significant effect on the overall particle deposition rate.
Aerosol; Turbulent flow; Micro-channel
X513
A
0258-0918(2021)06-1260-09
2020-10-23
国家科技重大专项项目(2019ZX06004013)
涂 卓(1995—),湖北荆门人,硕士研究生,现主要从事反应堆严重事故方面研究
曹学武,E-mail:caoxuewu@sjtu.edu.cn

