考虑通信延时的直流微网分组一致性控制策略研究

梁海峰， 丁锦睿， 边 吉

(华北电力大学 分布式储能与微网河北省重点实验室，河北 保定 071003)

0 引 言

微电网是由分布式电源、换流器、负荷以及储能装置等汇聚而成的小型发配电系统[1]。其可以通过联络点与大电网相连，工作在并网模式下。当大电网发生故障时，微电网可以运行在孤岛模式下，实现自我管理和控制。并且微电网可以分为交流微电网[2]和直流微电网[3]，相较于交流微电网，直流微电网可以减少电能转换的次数，不用跟踪系统的频率和相位，有效地提高系统的效率和可靠性。

在传统的直流微电网控制方法之中，多微源之间的协同控制方法多采用集中式或分散式的控制方法[4]。然而，传统的分散式控制，由于直流微网中线路阻抗的存在，属于有差控制，在母线电压和功率分配方面存在偏差[5]。而集中式控制虽然可以平衡母线电压和功率分配的精度，但可靠性存在问题，集中控制器的故障会影响整个系统的稳定[6]。

基于一致性的控制方法有效地解决了传统的集中式控制和分散式控制的缺点，并集合两者的优点，是一种有效的分布式系统控制方法[7]。基于一致性算法的分布式控制依托稀疏通信，每个受控节点仅需要本地测量信息和相邻节点的测量信息即可使整个系统的控制变量达到一致性，较传统的控制方法有更好地灵活性和可靠性[8]。

目前在直流微电网的分布式控制领域，国内外专家已经对一致性算法的应用开展了相关的研究。文献[9]对连接在同一母线上的储能单元提出了一种基于PI一致性的算法的电压优化控制策略，将控制问题转化为优化问题，但该控制策略对实际系统中通信延时对控制效果的影响没有具体的推导。文献[10]对微电网群的协同控制提出了一种基于离散一致性的智能多级控制策略，通过建立对角元素不为零的随机矩阵消除通信延时对收敛稳定性的影响。一致性算法不仅需要考虑通信延时的问题，状态观测器的初值也可能对最终收敛结果产生影响。文献[11]在传统的基于一致性的控制方法的基础上，加入抗干扰观测器，有效地提高收敛值的准确性。

文献[9-11]都是在一致性协调控制下，系统中所有智能体最终收敛到一致的状态，但随着系统中智能体数量的增加，最终达到一致性的时间也会相应的增加。为解决这一问题，基于分组一致性算法的控制策略[12]被应用于直流微电网的控制中。文献[13]应用离散分组一致性算法对双母线结构直流微电网内的电压观测器分别编组，使之分别快速收敛。但其没有考虑通信延时和一致性过程中可能出现的电流或电压观测器受到扰动的情况。

本文提出一种基于分组一致性算法的自适应下垂控制方法，不仅考虑实际系统中存在的通信延时的影响，而且加入抗干扰环节，提高了系统达到一致性的收敛速度和精度，并且平衡了母线电压波动和功率分配精度。

1 微电网的结构和传统下垂控制的缺陷

1.1 多母线结构直流微电网

早期的直流微电网只含有一条公共的直流母线[14]，当该母线发生故障时，会影响整个微网的稳定性和供电可靠性，而且直流功率单元的电压等级并不相同，因此出现多母线结构的直流微电网[15]，其能够实现不同类型、容量和直流电压等级的分布式电源、储能系统和负荷等的接入。为了简化分析，本文仅考虑孤岛模式下双母线结构的直流微电网的协同运行，其结构如图1所示。

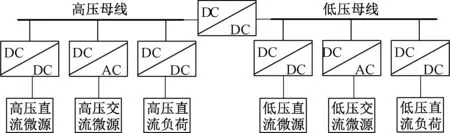
图1 多母线结构直流微网示意图Fig.1 Structure diagram of multi-bus DC microgrid

高压和低压母线分别实现区域自治，根据各自系统中微源和负荷的运行状态进行动态地调整。并且只有当其中任一区域功率不足而另一区域功率盈余时，两母线之间的换流器才会工作，从而维持整体系统的经济、有效地运行。

1.2 传统下垂控制的缺陷

图1中的六节点的双母线结构[16]的直流微电网的戴维南等效模型如图2所示。传统的阻性下垂控制方程[17]如下：针对任意第j个微源，当其向外供电时，存在以下方程：

Uoi=Uref-RdiIoi,i=1,2,…,n

(1)

式中:Uoi为第i个换流器的输出电压；Uref为第i个换流器参考输出电压；Rdi为第i个微源的下垂控制系数；Ioi为i个微源的输出电流。

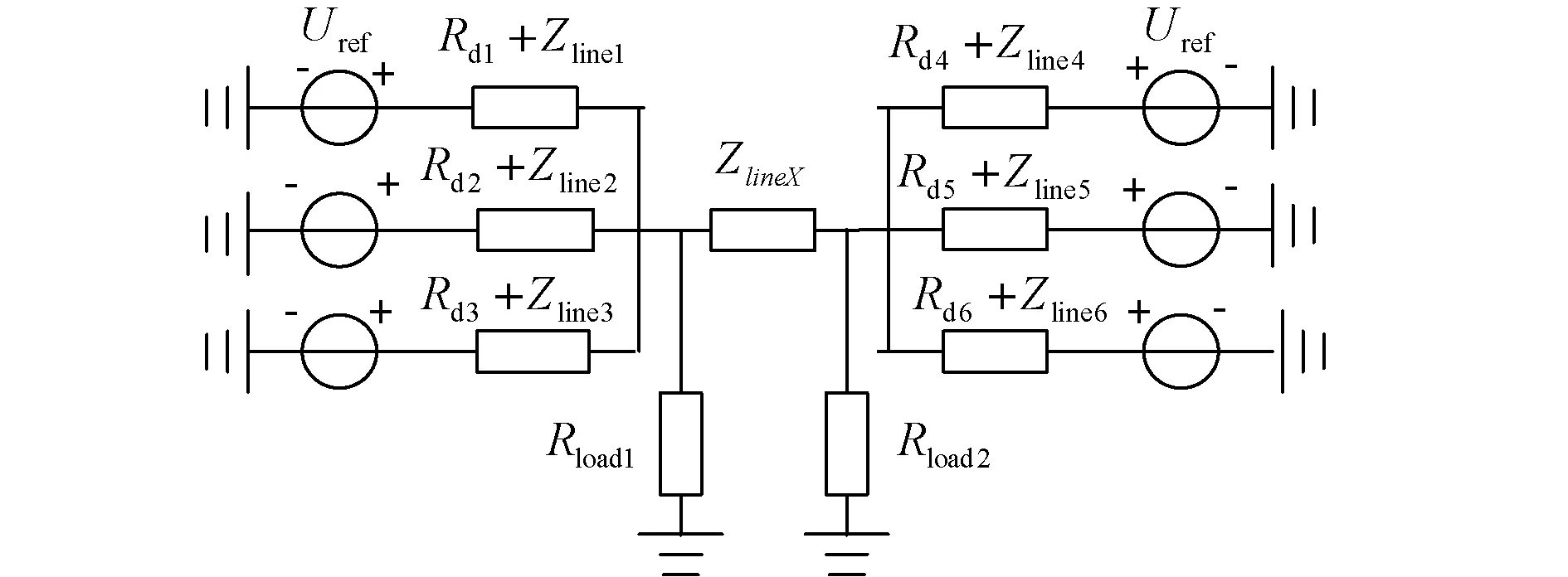
图2 双母线结构直流微电网戴维南等效模型Fig.2 Thevenin equivalent model of dual-bus DC microgrid

由式(1)可知，要使两母线区域内的功率单元分别实现功率精分，即要使各换流器的输出功率与自身额定功率成正比[18]，各节点的输出电流应满足下式：

(2)

式中：Xlinei为第i个换流器到其所在母线的线路阻抗；ni-j为第i个换流器和第j个换流器的额定功率之比。图2中XlineX为两母线之间线路的等效阻抗；Rload1、Rload2分别为两母线的等效负载电阻。但在实际控制过程中，线路阻抗往往无法确定或者会发生变化，此时传统的阻性下垂控制策略由于下垂系数固定，很难满足式(2)，达到功率的精确分配。

因此，为了实现直流微电网中各微源功率的精确分配，同时维持母各线电压的稳定。本文提出了基于分组一致性算法的多母线结构直流微电网控制策略。

2 考虑延时的分组一致性算法

2.1 分组一致性算法和最大通信延时

在一致性控制过程中，为了使系统快速有效地实现控制目标，多智能体需要尽快达到收敛。然而一致性协调控制中随着智能体数量的增加，系统达到收敛的时间会不可避免地增加，并且不同的智能体可能需要收敛到不同的目标值。因此文献[13]采用分组一致性算法来实现系统的快速收敛，并且各子网可以收敛到对应的不同目标值。但通信延时对一致性控制的收敛过程影响同样很大，本文提出考虑延时的分组一致性算法，同时给出系统最终收敛时能够承受的最大通信延时并给出相应证明。

当系统的通信延时小于本文所给出的最大通信延时，通信延时对系统收敛情况的影响文献[19-21]已给出具体分析，本文不再对其进行建模分析，主要考虑最大通信延时对系统最终能否收敛的影响。

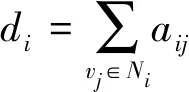
当拓扑结构为无向图、强连通平衡图时，可以得到如下的平均分组一致性[22]控制协议：

(3)

其中

∀i,j∈L1,aij≥0;∀i,j∈L2,aij≥0

(4)

(5)

式中:xi为第i个换流器的控制变量;τ为系统的通信延时。在式(3)中,为了平衡两个分组之间的相互影响，还需满足以下两个条件[23]：

(6)

(7)

若式(3)能够逐渐达到分组一致性[24]，系统的通信延时τ还需要满足下式：

(8)

(9)

2.2 最大通信延时的证明

对如式(3)所示的分组一致性算法能够收敛的最大通信延时，即式(8)进行证明，需要使用以下三个引理：

引理1[25]如果拓扑连通图G为连通的二分图，并且D和A分别是G的结点矩阵和邻接矩阵，那么矩阵D-A的秩为n-1。

引理2[26]对于任意γ∈[0,1)，当ω∈R时，此时凸包γCo(0∪{Ei(jω),i∈N}不包含(-1,j0)，其中

(10)

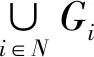
首先对式(3)做Laplace变换，可以得到系统的特征方程为det(sI+L(s))=0,其中I为单位阵，L(s)的定义如下：

(11)

令

F(s)=det(sI+L(s))

(12)

由系统稳定性判定的原理可知，只有F(s)零点都具有负实部或者s=0，如式(3)所示的平均分组一致性控制协议才能达到分组一致性。接着分两种情况对其进行分析。

(1)当s=0时，F(s)=det(D-A)，由引理1可知，s=0为F(s)的唯一零点。

(2)当s≠0时，令

P(s)=det(I+G(s))

(13)

其中

(14)

若P(s)的零点都具有负实部，则F(s)的零点也都具有负实部，则控制协议(3)能达到平均分组一致性。

令s=jω，对于式(14)，根据广义Nyquist准则，如果∀ω∈R，λ(G(jω))的Nyquist曲线不包含点(-1,j0)，则式(14)中所有零点均具有负实部。

根据盖氏圆盘定理，矩阵G(jω)的特征值λ(G(jω))满足：

(15)

且

(16)

式中:C为复数域，由式(16)可知，圆盘的中心Gi0(jω)为

(17)

当圆盘的中心Gi0(jω)的Nyquist曲线随着ω∈R变换时，圆盘Gi也随着变化。假设复平面的原点为O，O与Gi0连线的延长线交与圆盘的边界圆周于Wi点，已知随着Gi的变化，端点Wi的轨迹为

(18)

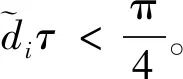
令γ=max{γi,i∈N},显然当γ<1，∀i∈N，下式成立：

(19)

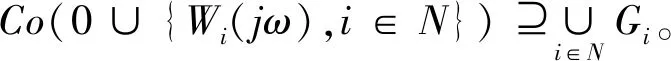
所以特征值λ(G(jω))的轨迹不包含(-1,j0)，则式(13)的特征根都具有负实根，可以得到当系统延时满足式(8)时，一致性控制协议(3)能够逐渐达到平均分组一致性。

3 基于考虑延时的分组一致性算法的自适应下垂控制

3.1 分组一致性的通信架构

本文将系统中每一个微源看作一个独立的智能体，将具有双母线结构的直流微电网上的微源按所处母线电压的不同分为两组，高、低压母线上微源的观测器节点下标集合，分别记作Lh和Ll；Nhi和Nli分别为高低压母线中的微源集合,其分组一致性通信框架的示意图如图3所示。

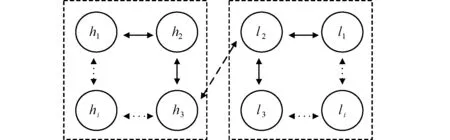
图3 分组一致性通信框架示意图Fig.3 Framework of communication based on group consensus algorithm

在控制策略运行的过程中，高、低压母线上的观测器采集所需信息，并分别在各自子网内进行信息交互，同时不同母线间的边界节点也交换信息，可以优化整体系统的控制效果。当任意母线的功率发生不平衡时，两母线间还可以进行能量交换，维持母线电压的稳定。

3.2 电压恢复一致性迭代

在分组一致性的控制过程中，通信系统总不可避免的存在通信延时的问题，当延时过大时，系统的一致性迭代就难以达到收敛。因此本文给出了当采用分组一致性算法的系统能够稳定时的通信延时τ的范围及其证明，当τ满足式(8)的条件时，该系统就能达到平均分组一致性。

在实际的应用过程中，在进行一致性迭代时电流和电压观测器所观测到的数值可能会受到干扰，从而影响一致性算法的收敛精度。因此本文在分组一致性算法的基础上，加入抗干扰状态观测器，电压恢复一致性迭代具体如下式所示：

(20)

其中

(21)

(22)

(23)

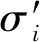
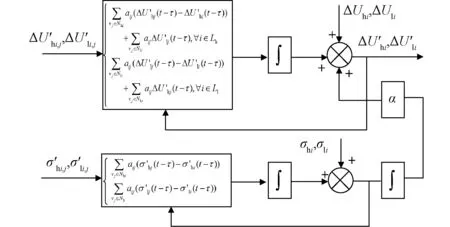
图4 电压恢复一致性迭代Fig.4 Voltage recovery based on consensus iteration

根据式(23)可得

(24)

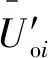
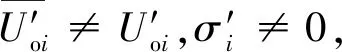
经过多次一致性迭代过后，高、低压母线上的功率节点上的电压会分别收敛到Uoh[∞]和Uol[∞]。

3.3 下垂系数自适应控制

在传统的阻性下垂控制中下垂系数固定，由于线路的阻抗可能无法测量或者在系统运行的过程中会发生变化，导致直流微电网无法在满足母线电压稳定的同时保证功率精分。因此本节提出了基于分组一致性算法的下垂系数修正的控制策略。

直流微网系统中各微源的额定容量存在差异，因此在获得各母线电压的平均值后，需要根据微源的负载能力来调节其输出功率，由式(25)来计算各微源的电流的标幺值：

(25)

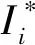
(26)

结合式(1)、(20)和(26)，可得对应的阻性下垂系数Rdi:

(27)

式中:Rdi(t)为第i个微源在第t时刻的下垂系数。

设备级控制由PI控制器完成，根据式(27)得出的修正后的下垂系数，用以对电压和电流做出相应的具体调节，从而在维持电压稳定的同时，实现功率精分。

4 仿真验证

4.1 仿真模型及参数

本文通过建立MATLAB/Simulink仿真模型，对所提出的适用于多母线结构的直流微电网的分组一致性控制策略进行分析，来验证本文所提出的控制策略的有效性。

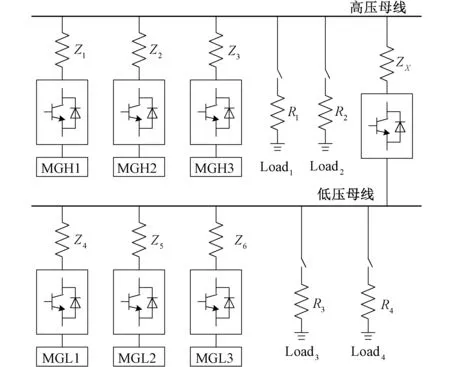
图5 双母线结构直流微网仿真模型 Fig.5 Simulation model of dual-Bus DC microgrid

仿真所搭建的双母线结构直流微网结构示意图如图5所示。在该仿真图中共包含3个高压直流微源MGH1、MGH2和MGH3，以及3个低压直流微源MGL1、MGL2和MGL3，且分别位于高、低压母线上。两母线通过换流器连接进行功率交换，且每个母线上各有两个阻性负载，分别记作Load1到Load4，其对应的负载阻抗分别为R1到R4，可以在不同的时间进行开闭，模拟微网负荷变化的情况。仿真中的具体参数如表1所示。

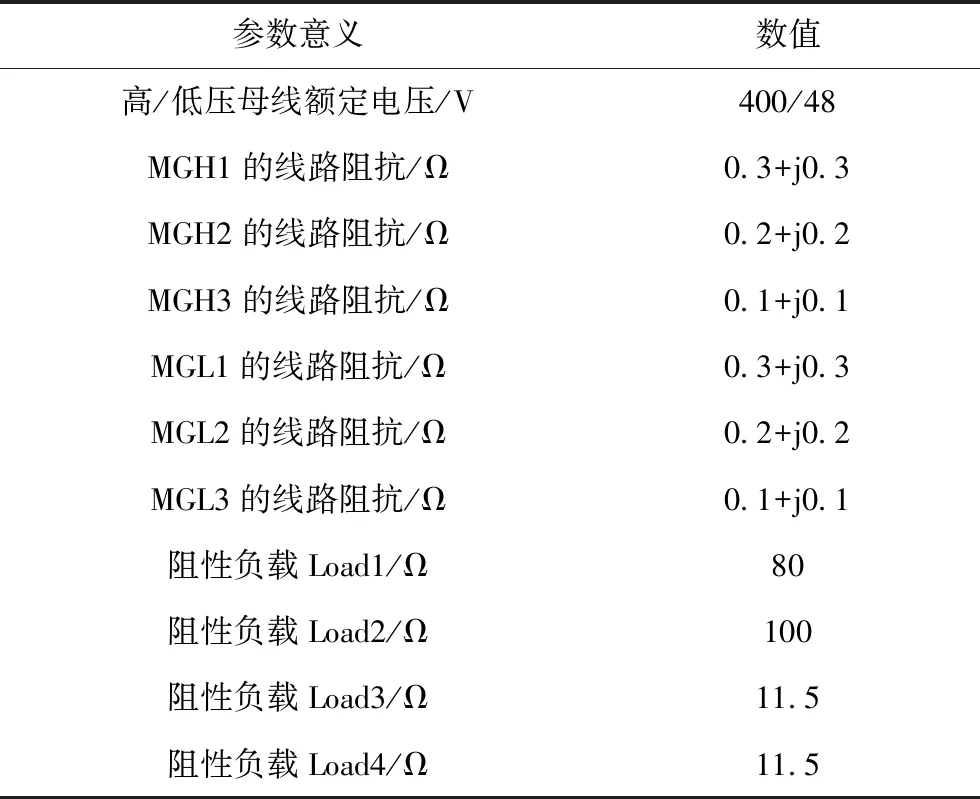
表1 直流微电网参数

4.2 分组一致性最大延时分析

MGH1-3和MGL1-3的换流器出口处电压和电流观测器依次记作智能体Agent1-Agent6，其中，Agent1-Agent3位于高压子网内，同时Agent4-Agent6位于低压子网内，图5对应的通信拓扑如图6所示。

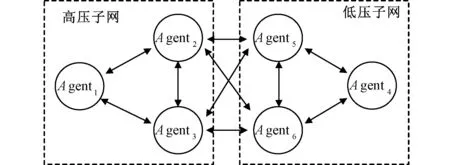
图6 微网通讯拓扑结构Fig.6 Communication topology of microgrid

假设如图6所示的拓扑结构下，当两微源间存在通信时，其通信权值均为1，并且通信权重还需满足式(4)、(5)、(6)和(7)，则该拓扑结构的邻接矩阵A为

(28)

结合式(8)和(28)计算可知，该仿真系统的最大通信延时τ为0.3 926 s。该仿真系统在0到2 s内高压和低压子网内分别只有负荷Load1和Load3接入系统，且0到1 s内微网采用传统下垂控制方法，在1 s时切换至本文所提出的考虑通信延迟的一致性控制策略。本节在该通信拓扑结构下，给通信延时为0.39 s和0.4 s时该直流微网中各微源的电流和电压的变化情况，即分别为通信延时小于和大于由式(8)得出的最大通信延时的情况。

图7(a)和7(b)分别为通信延时为0.39 s，即小于最大通信延时，微网切换控制策略时，微源的电流和电压的波形图。图7(a)中，1 s以前微网采用传统下垂控制策略，由于各微源所在的线路的阻抗不同，微网系统内的负荷不能够精确分配。在1 s时系统切换至本文提出的考虑延时的分组一致性控制策略，因为此时通信延时小于该系统所能承受的最大通信延时，在1.08 s时，高压和低压子网分别收敛于1.64 A和1.40 A，实现各子网内微源功率的精确分配。

图7(b)中在高压和低压子网内微源在1 s前由于线路阻抗的差异，换流器出口电压不尽相同，当切换控制策略后，各子网内微源均在1.15 s时收敛于各自子网的额定电压。

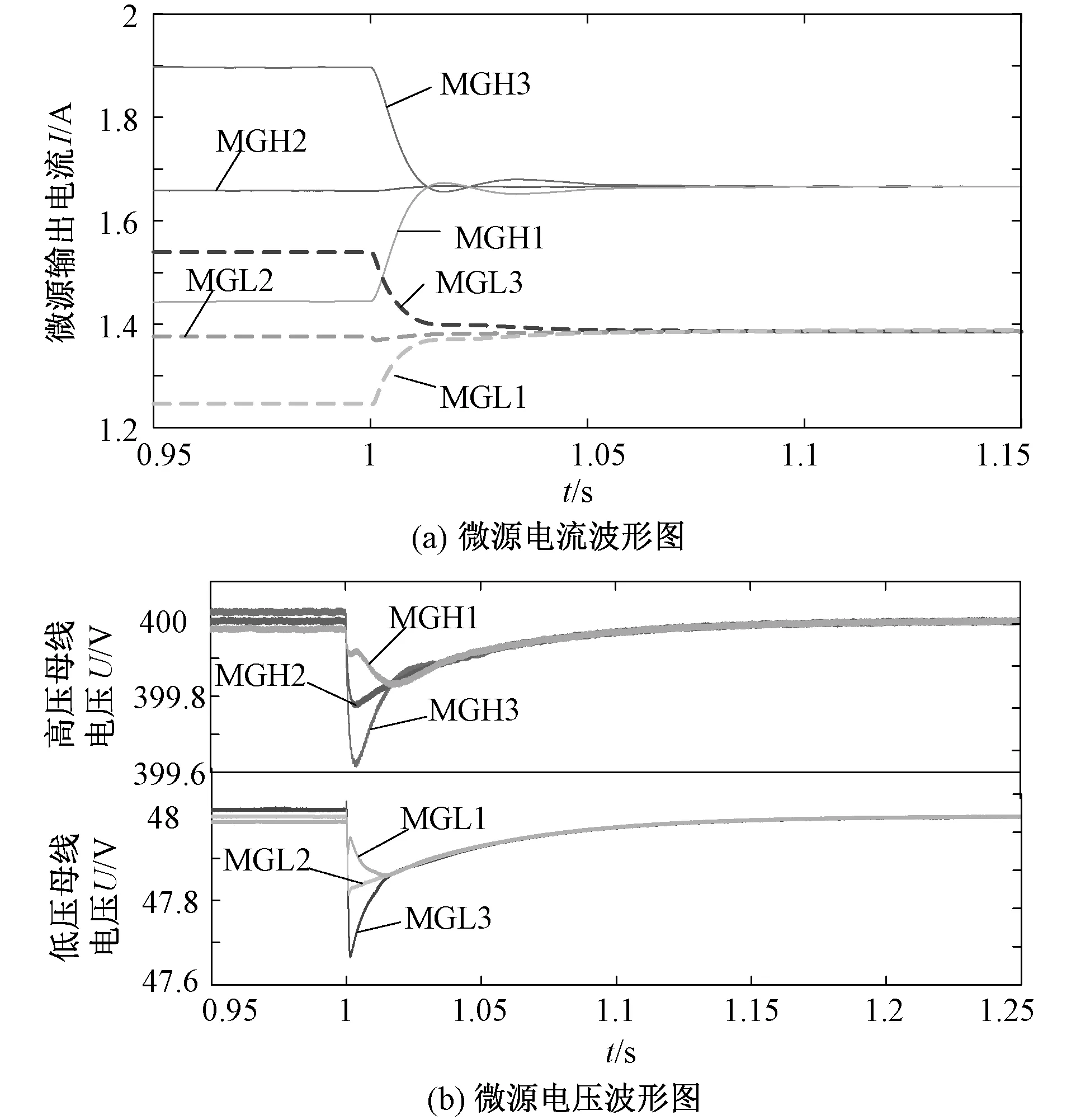
图7 通信延时为0.39 s时微源电流和电压波形Fig.7 Micro-sources current and voltage waveform when communication delay is 0.39 s

而图8为通信延时为0.4 s时，即大于最大通信延时，微网内各微源输出电流的波形图。由于此时的通信延时大于由式(8)所得出的系统能承受的最大通信延时，各微源的输出电流在1.2 s之前处于振荡状态，系统稳定之后最终也不能够达到收敛。

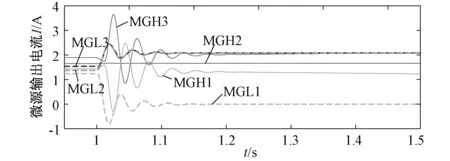
图8 通信延时为0.4 s时微源电流波形Fig.8 Micro-sources current and voltage waveform when communication delay is 0.4 s

因此，双母线结构的分组一致性控制策略只有当通信延时满足式(8)时，系统才能够达到平均分组一致性。

4.3 子网间通信故障分析

微电网各子网内发生通信故障时的分析在文献[28]中已经进行具体阐述。本文对双母线结构的微电网的子网间通信发生故障的情况进行分析。当如6所示的通信拓扑中高低压子网间的通信线路全部故障时，直流微网的通信拓扑结构变为了两部分。该仿真分析在该极端工况下，直流微网中各微源电压和电流的变化情况。图9为通信延时为0.39 s时，子网间发生通信故障时的电流和电压变化波形图。

由于此时两子网间通信发生故障，两子网只能获得各自子网内微源的信息，在相同通信延时下，会影响微源达到一致性的时间。图10(a)中高压和低压子网中电流达到收敛的时间分别为1.12 s和1.15 s，均大于通信正常时微网电流达到分组平均一致性的1.08 s。图10(b)中高压和低压子网中电压再次恢复到额定电压的时间分别为1.28 s和1.32 s，也大于通信正常时的恢复时间。

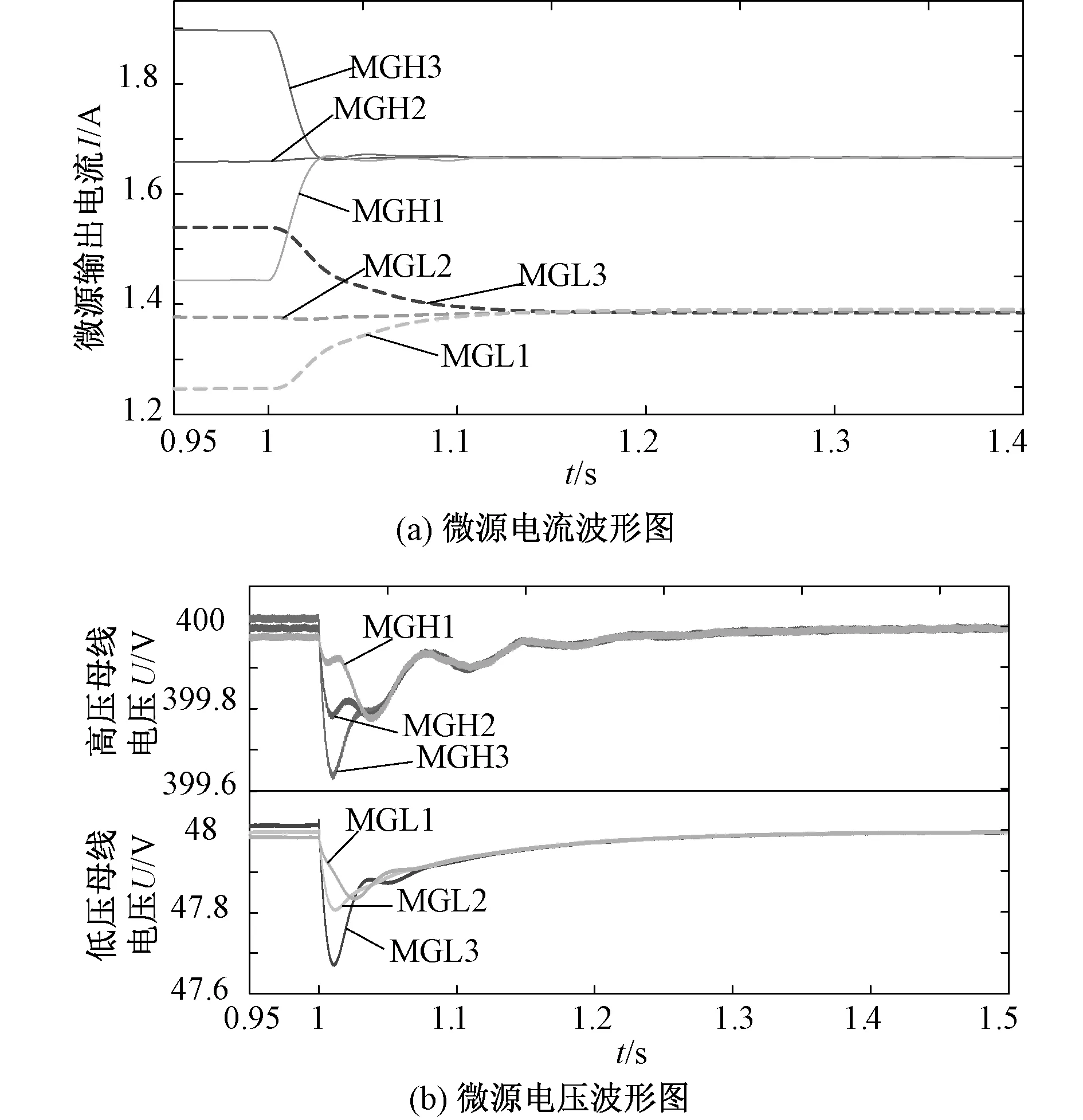
图9 子网间发生通信故障时微源电流和电压波形Fig.9 Micro-sources current and voltage waveform when communication failure occurs between sub-nets

因此当子网间通信发生故障时，会使系统达到收敛的时间增长，且两子网达到稳态的时间不相同，不利于系统的稳定。

4.4 系统负荷扰动分析

由于分布式系统存在间歇性和波动性，微电网实际运行的过程中系统功率也会发生波动，本文对双母线直流微电网系统发生负荷变化的情况进行研究。当微电网高压和低压子网间通信正常，且系统的通信延时为0.39 s时，负荷Load1和Load3在0到3 s内均接入系统。在2 s时，负荷Load2和Load4接入微电网，负荷变化时，直流微电网的电流和电压的波形图如图10所示。

图10(a)为系统负荷变化时的电流波形图，当系统负荷突变时，微电网内微源之间先按下垂特性增发功率，然后相互通信，调整各自的下垂系数，高压和低压子网内的微源均在2.05 s时达到收敛。图10(b)为系统负荷变化时的电压波形图，两子网电压在2.15 s时恢复到额定水平。因此该控制策略能够有效的应对系统负荷变化的情况。

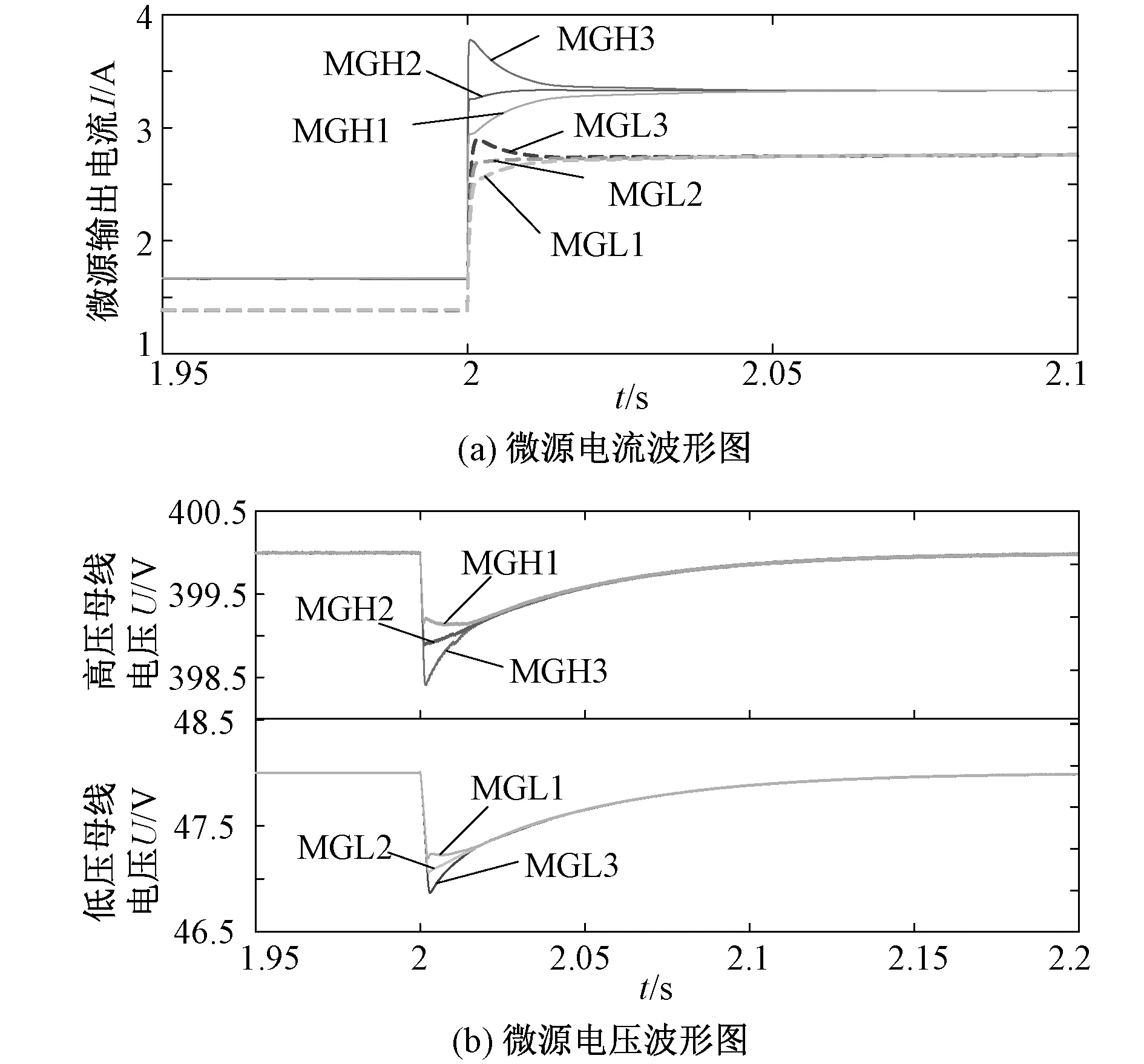
图10 系统负荷变化时微源电流和电压波形Fig.10 Micro-sources current and voltage waveform when load changes

4.5 观测器扰动分析

微电网运行过程中，各微源的电压和电流观测器可能会受到扰动，从而影响一致性算法的控制效果。在3 s时，微电网中分别对位于MGH1和MGL1上的电压观测器分别受到1 V和0.3 V阶跃信号的干扰，图11(a)和(b)分别对应电压观测器受到干扰后，微电网中各微源电流和电压的波形图。

由于抗干扰观测器的调节，图11(a)中高压和低压子网中电流于3.1 s再次达到收敛，实现平均分组一致性。而图11(b)中各微源的电压于3.15 s再次收敛于电压的额定值。

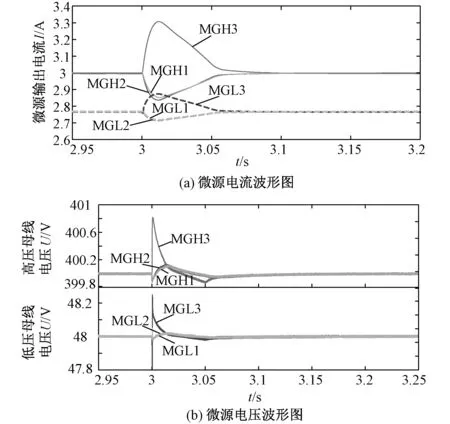
图11 观测器受到干扰时微源电流和电压波形Fig.11 Micro-sources current and voltage waveform when the observer is disturbed

5 结 论

本文提出了一种考虑通信延迟的多母线结构直流微电网一致性控制策略，通过理论推导，得出微电网电压电流达到平均分组一致性所能承受的最大通信延时，并通过MATLAB/ Simulink仿真对理论做出验证。

进行一致性迭代时可能存在电压或电流观测器所观测到的数值受到干扰的情况，从而影响一致性算法的收敛精度。该控制策略加入了抗干扰观测器，能够有效提高系统内各子网电压的收敛精度。

本文根据一致性算法得出的电压和电流，动态地调整下垂系数，能够实现微电网的功率精分和母线电压稳定。并且不同母线上的微源能够实现功率的交换，提高了整体系统的可靠性和适应性。