设置新型自复位阻尼器的隔震结构动力响应控制效果分析*

田 坤

(上海市建筑科学研究院有限公司上海市工程结构安全重点实验室，上海 200032)

0 引言

在罕遇地震作用下，结构会发生较大变形，从而导致严重损伤，甚至发生倒塌，且残余变形较大，造成震后修复成本高、难度大。因此，减小结构在地震作用下的动力响应与残余变形是土木工程领域具有挑战性的课题。为解决上述问题，可采用具有可恢复功能的结构，经地震作用后，该类结构无须修复或稍加修复即可恢复使用功能[1]。为保证结构具有可恢复功能，通常在结构中设置自复位装置。

1 自复位装置类型

按构造形式及恢复力提供构件可将自复位装置分为以下类型。

1)预应力筋式自复位装置

Christopoulos等[2]研发出自复位耗能钢支撑装置，使用芳纶纤维筋作为恢复力提供构件，并在支撑外筒设置摩擦板，以提高耗能能力。受芳纶纤维筋变形能力限制，该装置行程受限。为此，Erochko等[3]进行了改进，将自复位筋进行层叠串联，提出可提高变形行程的层叠式自复位装置，并进行了力学性能试验研究。

2)形状记忆合金式自复位装置

Zhu等[4]提出由2块钢支撑板和形状记忆合金索组成的自复位摩擦支撑装置，依靠形状记忆合金索提供恢复力，依靠支撑板间的摩擦作用耗能。Khader等[5]提出的自复位支撑装置主要由2块钢板组成，通过形状记忆合金索将2块钢板相连，以提供恢复力，依靠钢板间的摩擦作用耗能。Ozbulut[6]提出黏弹性自复位阻尼装置，在阻尼器外部缠绕形状记忆合金索，通过形状记忆合金索提供恢复力，依靠黏弹性材料剪切变形耗能。Miller等[7]提出自复位屈曲约束支撑装置，在常规屈曲约束支撑外部设置预张拉形状记忆合金棒，通过形状记忆合金棒提供恢复力，依靠屈曲约束支撑耗能。董金芝等[8-9]提出使用大直径形状记忆合金棒的自复位装置，并通过拟静力试验验证了该装置具有良好的力学性能，该装置通过形状记忆合金棒提供恢复力。

3)钢弹簧式自复位装置

Dong等[10-12]设计了用于桥梁结构的自复位耗能支撑装置，通过拟静力试验研究了该装置的力学性能和破坏形式，并进行了参数分析，该装置通过碟形弹簧提供恢复力。蒋璐等[13]研发了设置碟形弹簧的自复位装置，并对设置该装置的单榀摇摆墙-框架结构进行了拟静力试验研究。Issa等[14]提出活塞式自复位支撑装置，并通过拟静力试验研究了该装置力学性能，该装置通过摩擦弹簧提供恢复力和耗能能力。徐龙河等[15-18]基于碟形弹簧，研发出多种自复位支撑装置，并通过拟静力试验研究了多种装置力学性能。

已有自复位装置多依靠构件间的摩擦作用耗能，随着往复运动次数的增加，在地震作用下，装置将发生变形，可能导致耗能能力和可靠度降低。在结构中设置阻尼器等消能减震装置，可显著减小结构在地震作用下的动力响应[19]，但常规黏滞阻尼器不具备自复位能力，为此，研发设置碟形弹簧的新型自复位阻尼器，并进行数值模拟分析，对比分析无控结构、设置常规黏滞阻尼器的隔震结构和设置新型自复位阻尼器的自复位隔震结构动力响应。

2 新型自复位阻尼器构造

新型自复位阻尼器构造如图1所示，主要由导杆、密封外筒和碟形弹簧组成，装置内部填充黏滞阻尼液，依靠碟形弹簧压缩变形产生的弹性恢复力实现自复位，通过内部耗能隔板等部件使黏滞阻尼液发生剪切和挤压，从而起耗能作用。

图1 新型自复位阻尼器构造示意

新型自复位阻尼器工作状态如图2所示，通过构造设计，可使阻尼器受拉和受压时碟形弹簧均处于压缩状态，从而为阻尼器提供弹性恢复力。

图2 新型自复位阻尼器工作状态示意

新型自复位阻尼器主要具有弹性自复位能力和耗能能力，将黏滞阻尼器和碟形弹簧滞回模型进行叠加，可得新型自复位阻尼器理论滞回模型，如图3所示。由图3可知，新型自复位阻尼器滞回模型呈双线性特征。

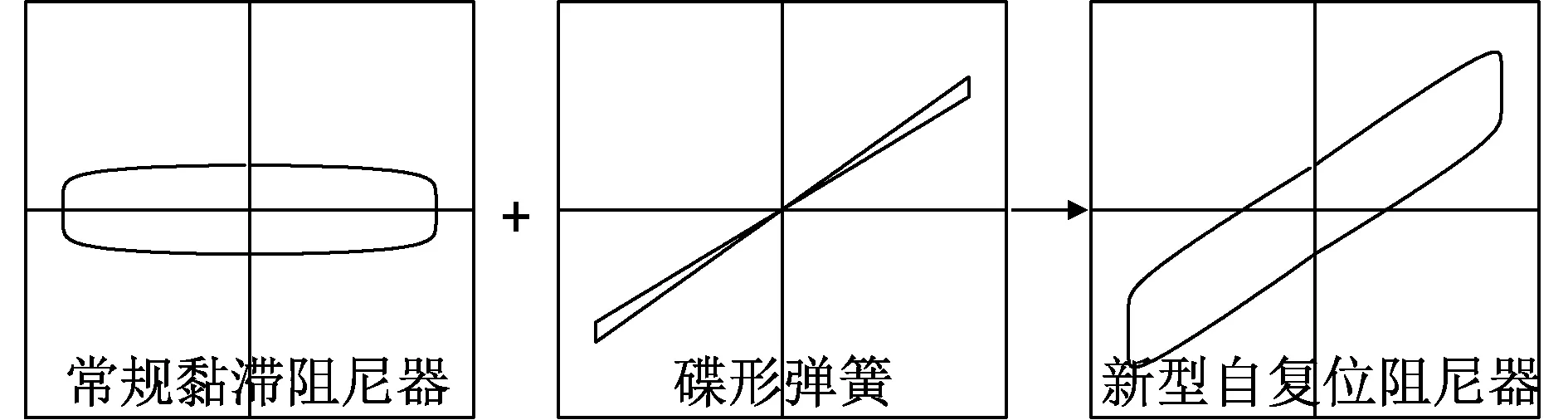
图3 新型自复位阻尼器理论滞回模型

3 有限元模型建立

采用有限元分析软件SAP2000建立12层无控结构质点系模型(见图4a)，对无控结构在地震作用下的动力特性与层间变形特性进行研究，分别在层间位移较大的位置(2，4，6，8层)设置常规黏滞阻尼器和新型自复位阻尼器，建立常规隔震结构质点系模型和自复位隔震结构质点系模型，分别如图4b，4c所示。数值模拟分析时选用El-Centro，Kobe，Loma，Taft波，地震波原始信息如表1所示，归一化地震波时程曲线与加速度反应谱如图5所示。

图4 有限元模型

表1 地震波原始信息

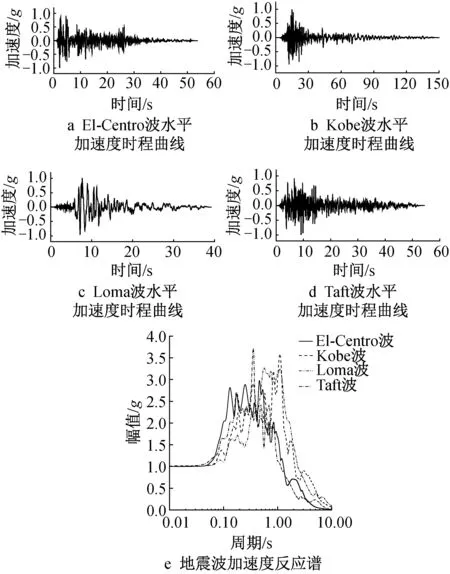
图5 归一化地震波时程曲线与加速度反应谱

4 结构动力响应分析

4.1 加速度

当地面峰值加速度为0.3g时，不同地震波作用下结构加速度放大系数如图6所示。由图6可知，3种结构加速度均随着楼层数的增加而增大，常规隔震结构与自复位隔震结构加速度较无控结构小。在El-Centro，Taft波作用下，自复位隔震结构加速度响应相对于常规隔震结构差别较小，在顶部个别楼层处加速度略放大；在Loma波作用下，自复位隔震结构1～9层加速度响应与常规隔震结构相当，但10～12层加速度减小；在Kobe波作用下，自复位隔震结构加速度相对于常规隔震结构明显减小。

图6 加速度放大系数曲线

当地面峰值加速度为0.3g时，Kobe波作用下常规隔震结构与自复位隔震结构加速度放大系数相对于无控结构减小率如表2所示。由表2可知，自复位隔震结构加速度响应控制效果优于常规隔震结构，其中加速度放大系数减小率最大值为8.59%。

由地震波加速度反应谱可知，Kobe，Loma波在1s(与结构一阶周期0.97s相近)处存在明显峰值段，造成结构动力响应增大，通过设置常规黏滞阻尼器和新型自复位阻尼器，可显著减小结构加速度，且新型自复位阻尼器对结构加速度响应的控制效果更显著。

表2 结构加速度放大系数减小率 %

4.2 位移

当地面峰值加速度为0.3g时，不同地震波作用下结构水平位移峰值和层间位移角峰值分别如图7，8所示，Kobe波作用下常规隔震结构与自复位隔震结构水平位移峰值和层间位移角峰值相对于无控结构减小率分别如表3，4所示。由图7和表3可知，3种结构水平位移峰值均随着楼层数的增加而增大；常规隔震结构与自复位隔震结构水平位移峰值均较无控结构小，尤其是在El-Centro，Taft波作用下；在Kobe波作用下，自复位隔震结构水平位移相对于常规隔震结构减小效果更显著，其中水平位移峰值减小率最大值为27.27%。由图8和表4可知，常规隔震结构与自复位隔震结构层间位移角峰值均较无控结构小，自复位隔震结构层间位移角控制效果更显著，其中层间位移角峰值减小率最大值为14.00%。

表3 结构水平位移峰值减小率 %

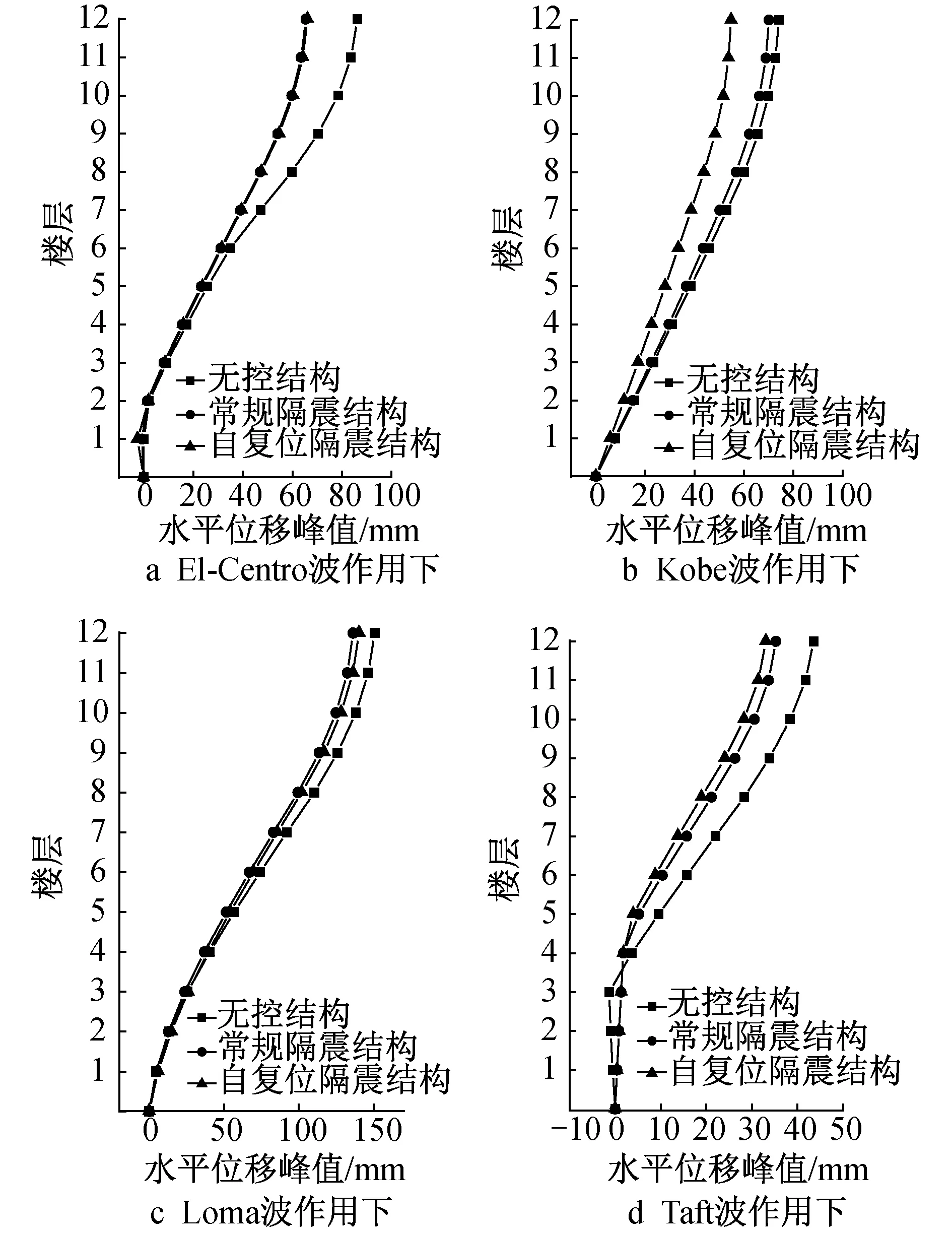
图7 结构水平位移峰值曲线

图8 结构层间位移角峰值曲线

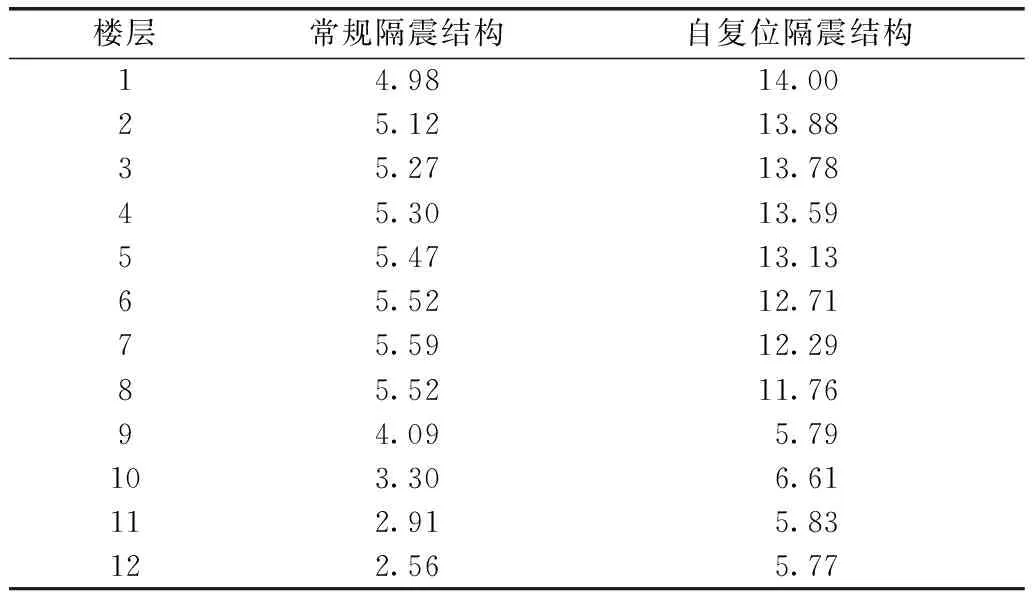
表4 结构层间位移角峰值减小率 %

4.3 滞回性能

当地面峰值加速度为0.3g时，不同地震波作用下常规隔震结构与自复位隔震结构4层处阻尼器滞回曲线如图9所示。由图9可知，新型自复位阻尼器滞回曲线饱满，耗能能力良好，呈双线性特征，与理论滞回模型相符。新型自复位阻尼器变形相对于常规黏滞阻尼器小，Kobe波作用下变形减小9%。

图9 阻尼器滞回曲线

5 结语

研发新型自复位阻尼器，并根据工作原理与力学特性建立阻尼器理论滞回模型。采用有限元分析软件SAP2000建立无控结构、常规隔震结构和自复位隔震结构模型，分别进行动力响应分析，得出以下结论。

1)当新型自复位阻尼器受拉和受压时，内部碟形弹簧均处于压缩状态，可为装置提供弹性恢复力。

2)新型自复位阻尼器不影响结构自振周期，可使结构加速度和位移响应得到有效控制，对位移响应的控制效果更明显。Kobe波作用下，自复位隔震结构加速度放大系数、水平位移峰值、层间位移角峰值减小率最大值分别为8.59%，27.27%，14.00%。

3)对于自振周期与地震动卓越周期相近的结构，新型自复位阻尼器动力响应控制效果优于常规黏滞阻尼器。

4)数值模拟计算得到的新型自复位阻尼器滞回曲线饱满，耗能能力良好，呈双线性特征，与理论滞回模型相符。