基于噪声抑制门的两级自适应线谱增强算法

马 凯 蔡昱明 王易川 程玉胜

①(海军潜艇学院 青岛 266000)

②(91001部队 北京 100036)

1 引言

随着舰船辐射噪声[1]的降低，从强海洋背景噪声中检测出弱的线谱[2]信号，是近年来水声信号处理[3]领域的一个重要研究内容。常用的声呐线谱检测[4–8]方法大都采用傅里叶变换处理方法，但该方法在低信噪比下线谱检测能力较差。1960年，Widrow和Hoff提出了最小均方误差(LMS)算法，因其计算量小且容易实现而得到广泛关注[9–14]，并用于自适应滤波[15,16]、自适应线谱增强等各个方面。自适应线谱增强[17–23](ALE)算法，可以有效抑制噪声，增强线谱，适合于强噪声背景下的信号检测。但其性能随着信噪比的降低急剧下降，针对此问题本文提出基于噪声抑制门的2级ALE算法，可有效地提高其在低信噪比下的性能。

2 基于噪声抑制门的降噪预处理

假设淹没在随机噪声中的CW(Continuous Wave)信号可表示为

图1 Rn(t)

图4为常规FFT方法得到的频谱图与经过噪声抑制门处理后的频谱图的对比，信号经过FFT处理后信噪比为2.6 dB，经过噪声抑制门处理后信噪比为12.2 dB，噪声能量得到明显抑制，信噪比提高了大约9.6 dB。

3 2级ALE算法

3.1 ALE算法原理

ALE算法是宽带噪声背景下检测单频信号或窄带信号的自适应谱估计技术，它不需要独立的参考信号，广泛应用于线谱检测、窄带检测等领域。

图5为自适应线谱增强器的原理框图，图中x(k)为 输入信号，s (k)为 单频或窄带信号，n (k)为高斯白噪声，则ALE的计算公式为

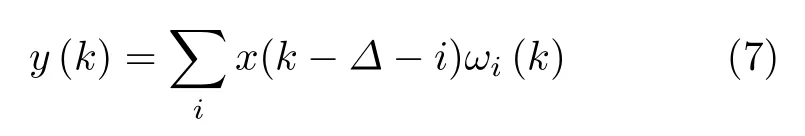
图2 Rs(t)

图3 噪声抑制门示意图

ALE算法在信噪比较高时效果较好，但当信号的信噪比较低时，算法性能下降较为严重，基于此，本文提出2级自适应线谱增强算法。

3.2 2级自适应线谱增强器原理

2级自适应线谱增强器是在1级自适应线谱增强器的基础上，结合频域自适应LMS算法，将输出信号y (k)与 误差信号e (k)的频谱作为第2级自适应LMS算法的输入，原理如图6所示。输入信号 x(k)经过1级ALE后得到线谱增强后的信号y (k)和误差信号e(k)， 此时误差信号e (k)中基本为噪声分量，不含有信号分量。将误差信号 e(k)的傅里叶变换作为参考信号，信号y (k)的傅里叶变换作为期望信号，输入到第2级自适应LMS算法中，则最后得到的输出信号即为经过2级自适应LMS算法增强线谱后的信号。

图4 2种方法频谱图对比

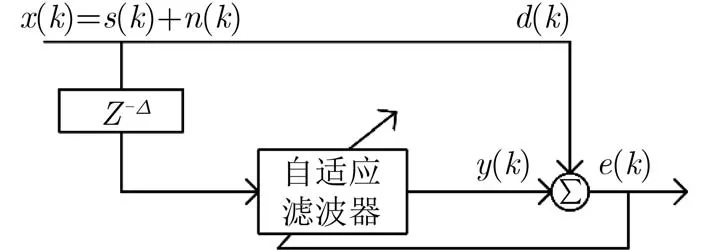
图5 ALE原理框图

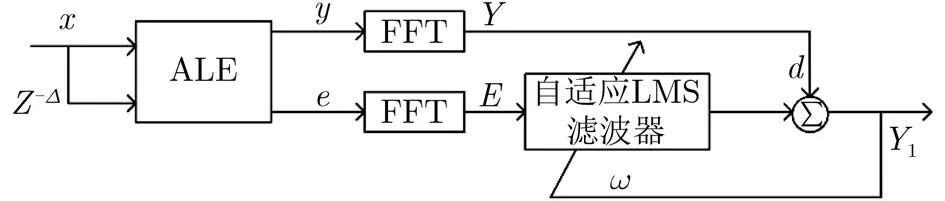
图6 2级ALE原理框图

则第2级自适应LMS算法的计算公式为

3.3 计算机仿真及海试数据处理

3.3.1 计算机仿真

输入信号为单频信号加高斯白噪声信号，信号频率为300 Hz，采样频率为1000 Hz，信号长度为10 s，信噪比为–19 dB。现定义局部信噪比：SNR=S/N, S 为线谱的能量， N为背景干扰的平均能量，以此来作为评价算法性能的一个标准。

图7为3种算法的频谱图，其中图7(a)为原始信号频谱图，从图中可以看出此时线谱能量较弱，背景干扰较强，信噪比为2.3 dB；图7(b)为经过1级ALE算法处理后的结果，从图中可看出，此时线谱能量相对加强，但由于信噪比较低，算法性能不是很好，信噪比为7.5 dB；图7(c)为经过2级自适应LMS算法处理后的结果，从图中可以看出线谱能量较强，背景较为干净，效果较好，信噪比为18.5 dB，相较于1级ALE算法，信噪比提高了11 dB。

下面验证算法在更低信噪比下的性能，将上述仿真条件中的信噪比改为–22 dB，其余不变。图8为更低信噪比下3种算法的频谱图，从图中可以看出，信号基本淹没在噪声背景中，经过1级ALE算法和2级ALE算法处理后，背景噪声能量都有所降低，信噪比分别为0.4 dB, 3.8 dB和6.5 dB，但两者性能都不是很好。

3.3.2 海试数据处理

图9(a)为原始信号的频谱图，线谱的频率分别为98 Hz, 124 Hz和257 Hz，除98 Hz线谱能量较强外，其他线谱信号能量较弱。图9(b)为经过1级ALE算法处理后的信号的频谱图，信号能量有所加强，线谱较为明显。图9(c)为经过2级ALE算法处理后的频谱图，此时背景较为干净，线谱能量较强。

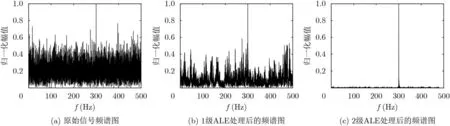
图7 3种算法的频谱图

图8 更低信噪比下3种算法的频谱图

图9 3种算法处理后的频谱图对比

为更直观地比较算法的性能，现对3种算法的频谱图沿时间轴做切片，提取某个时刻的频谱图作比较，并重新定义局部信噪比为： SNRi=Si/Ni，其中， Si为 某根线谱能量，Ni为以此线谱为中心的40个频点的能量的均值。

图10为某一时刻3种算法的频谱图比较。从图中看出，经过1级ALE算法和2级ALE算法处理后，线谱能量得到增强，噪声能量得到抑制，其中2级ALE算法优于1级ALE算法。

表1是3种算法的各线谱的信噪比的比较，可以看出，2级ALE算法相较于1级ALE算法，3根线谱的信噪比分别提高了0.8 dB, 1.4 dB, 0.4 dB。

通过仿真和海试数据处理可以看出，本文提出的2级ALE算法相较于1级ALE算法性能有较大提升，但当线谱能量较弱时，提升不明显，针对此问题，本文提出基于噪声抑制门的2级ALE算法。

4 基于噪声抑制门的2级ALE算法

考虑将噪声抑制门和2级ALE算法结合起来，提出一种基于噪声抑制门的2级ALE算法以提升算法的性能。下面通过仿真和海试数据处理加以验证。

4.1 算法处理流程

图11为本文提出的基于噪声抑制门的2级ALE算法处理流程，过程如下：

(1) 对接收信号s 进行相关处理，并将其通过噪声抑制门，得到处理后的信号 X；

(2) 将处理后的信号 X及其延时信号输入到1级ALE算法中，得到输出信号y 及误差信号e；

(3) 对信号y 及误差信号e 进行傅里叶变换得到信号 Y及误差信号E ；

(4) 将信号 Y及误差信号 E输入到2级ALE算法中 ，得到最终所需的信号频谱Y1。

4.2 计算机仿真

仿真条件同上，输入信号为单频信号加高斯白噪声信号，信号频率为300 Hz，采样频率为1000 Hz，信号长度为10 s，为验证算法在低信噪比下的性能，将信噪比设为–22 dB。

图12为3种算法的对比图，从图中可以看出，在原始频谱图中，300 Hz的线谱被淹没在噪声背景中，此时的信噪比为0.9 dB。经2级ALE处理后，300 Hz处的线谱虽有所加强，旁边杂乱的线谱较多，总体性能较差，此时信噪比为4.6 dB。而经过本文提出的基于噪声抑制门的2级ALE算法处理后，线谱能量得到较大增强，总体背景较为干净，此时信噪比为20.2 dB，相较于2级ALE算法，信噪比提高了15.6 dB。

4.3 海试数据处理

海试数据同上，采样频率为2048 Hz。图13(a)为原始信号频谱图，噪声背景较强。图13(b)为2级ALE算法处理后的频谱图，此时噪声背景有所减弱，线谱有所增强。图13(c)为经过本文提出的基于噪声抑制门的2级ALE算法处理后的频谱图，噪声背景较为干净，效果最好。

为更直观地比较3种算法的性能，按照3.2.2节中的处理方法，对频谱图的某一时刻数据进行切片，如图14所示。经过2级ALE算法处理后，噪声背景有所降低，线谱能量有所增强。而经过本文提出的基于噪声抑制门的2级ALE算法处理后，背景最干净，性能最好。

图10 同一时刻3种算法处理后的频谱图对比

表1 3种算法处理后的线谱信噪比比较(dB)

图11 基于噪声抑制门的2级ALE算法处理流程

图12 3种算法处理后的频谱图对比

表2是3种算法的各线谱的信噪比的比较，可以看出，基于噪声抑制门的2级ALE算法相较于2级ALE算法，信噪比分别提高了6.9 dB, 10.0 dB, 10.7 dB。

图15为另一段海试数据的处理结果，从图15(b)中可以看出，经2级ALE算法处理后，噪声背景有所降低，但能量较弱的线谱增强不明显，效果一般。图15(c)为本文算法处理后的结果，可以看出噪声背景得到较好的抑制，线谱能量得到一定增强，效果较好。

综上分析可得，信噪比较低时，基于噪声抑制门的2级ALE算法性能最好，但同时也存在一个问题，即当频谱中存在多条线谱时，弱线谱的增强幅度相对于强线谱的增强幅度较小，导致弱线谱在频谱图中不是很明显，下一步将针对此问题进行研究。

5 结束语

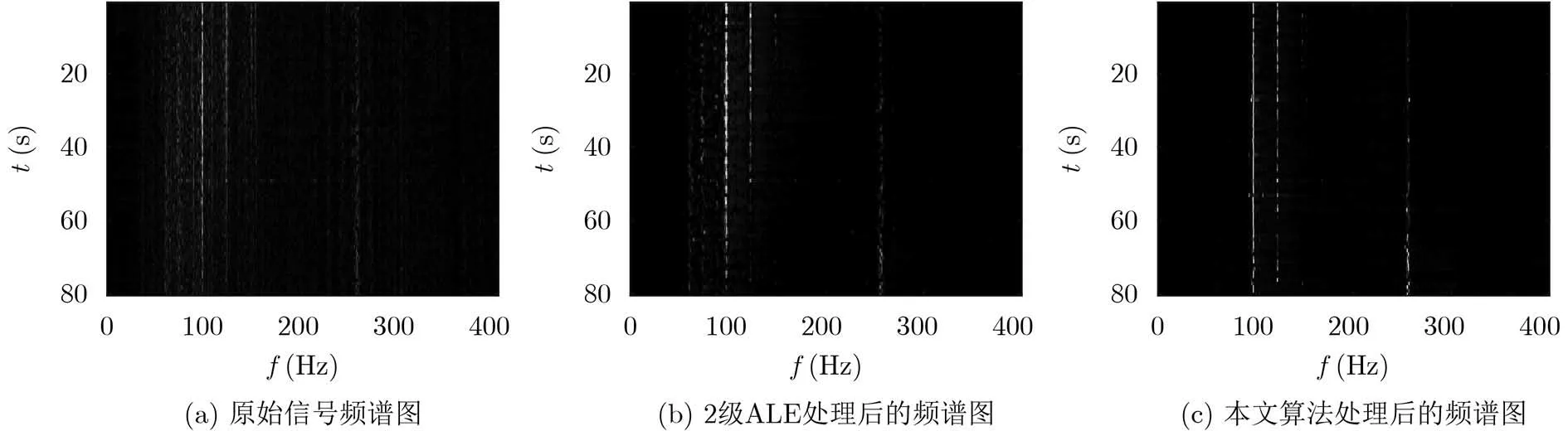
图13 3种算法处理后的频谱图对比

图14 同一时刻3种算法处理后的频谱图对比

表2 3种算法处理后的线谱信噪比比较(dB)

图15 3种算法处理后的频谱图对比

针对低信噪比下普通ALE算法对线谱增强效果有限的问题，提出了2级ALE算法，此算法性能较好，但当信噪比更低时，受限于自适应LMS算法的特性，2级ALE算法性能下降较为严重。基于此，本文利用噪声相关的特性，提出一种基于噪声抑制门的2级ALE算法，经过计算机仿真和海试数据验证，算法在低信噪比下有较好的性能表现。