跨谱段SAR散射中心多维参数解耦和估计方法
谢意远 高悦欣 邢孟道* 郭 亮 孙光才
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
②(西安电子科技大学信息感知技术协同创新中心 西安 710071)
③(西安电子科技大学空间科学与技术学院 西安 710071)
④(西安电子科技大学物理与光电工程学院 西安 710071)
1 引言
近年来,随着国内外微波光子技术和器件的推动与快速发展,雷达的带宽提升了一个数量级,从一般的1 GHz带宽增加到10 GHz以上,使雷达具备了收发和处理跨谱段大带宽信号的能力,极大地提高雷达的距离分辨能力,成像分辨率有望从分米级提升到毫米级[1–3],另外,带宽的提高,更加凸显了目标回波的频率依赖性,使得目标结构部件对不同频率信号的差异性变得更加明显。相比传统方法着重依赖目标部件的视角依赖性进行估计的手段,结合目标部件回波的角度依赖性与频率响应特性应能够更好地实现目标部件的识别[4,5]。高效、精确地提取目标频率、角度依赖特性是实现基于目标电磁特性目标识别分类的基础。
关于散射中心参数提取的方法已有大量文献进行研究。文献[6]实现了属性散射中心模型的位置参数和其他参数的解耦合,降低了复杂度,但是由于其在图像分割前使用Radon变换粗成像,在大视角情况下成像聚焦效果不好,影响后续独立散射中心的提取。基于幅相分离的属性散射中心方法[7]考虑散射模型的幅度相位项可分离,降低了算法复杂度;基于属性散射中心模型的RELAX算法[8]引入快速傅里叶算法,提高搜索效率;基于稀疏信号分析的属性散射中心提取算法[9]将高维的联合字典简化为两个低维字典[10],降低了资源需求,但它们都仅适用于带宽较小的情况,没有考虑频率依赖特性的影响。
在跨谱段雷达系统条件下,信号量相比传统系统成倍增加,信号中包含的目标信息量骤增,然而基于小带宽下低分辨图像参数估计方法,无法完全提取信号中包含的目标精细特性信息。其次,在超高分辨的情况下,目标的频率依赖特性更加明显,电磁模型的参数维度增加,参数估计困难。为了解决这些问题,研究跨谱段情况下电磁散射模型的参数估计问题是非常必要的。
本文提出跨谱段SAR散射中心多维参数解耦和估计方法,实现了大带宽大转角[1,11]的情况下对目标部件精确长度、角度、频率依赖特性的提取。本方法利用了大带宽大视角成像分辨率高的特性,首先对各电磁散射体的位置参数进行精确提取;在获取电磁体的精确位置参数之后,提出结合坐标下降法(Coordinate Descend Algorithm, CDA)和Hooke-Jeeves算法,将复杂多维耦合参数估计问题转化为多个循环迭代的1维参数估计问题,能够高效地实现电磁散射体角度、频率依赖特性的精确估计。通过以上估计结果,可以进一步获取散射体结构,突破了信号分辨率对散射体的识别限制。最后通过仿真实验结果,验证了本文方法的有效性。
2 跨谱段散射中心模型的属性参数分析
在大带宽和大转角成像条件下,散射中心的后向散射回波对频率和方位角度表现出强依赖性。对目标散射中心进行参数化建模,准确高效地描述目标在高频区域的散射特性是算法设计的前提条件。属性散射中心模型能够利用一组特征参数的不同组合来描述典型散射中心的几何和物理属性,表达式简洁,描述较为精确。它利用幂函数建模散射中心幅度的频率依赖关系;利用sinc函数建模散射中心幅度对方位角度的依赖特性[12]。由于属性散射中心的诸多优点,本文以属性散射中心为理论模型对散射中心的频率和角度依赖特性进行描述。根据几何绕射理论和物理光学理论,当目标为电大尺寸目标时,它的散射回波可以用若干个离散点的散射回波的相干叠加近似表示[13,14]。散射中心p 的响应与频率和角度依赖关系由散射点的几何结构、电磁散射机理和极化特性决定,其回波表达式为


3 跨谱段大转角条件下的目标部件长度、角度、频率依赖性提取
针对解决跨谱段大转角条件下基于电磁模型的特性提取问题,本文采用属性散射中心模型对散射体进行参数化描述。首先利用极坐标格式算法对大视角下的目标回波成像得到位置参数,再结合坐标下降法将高维参数估计问题简化为循环迭代的1维参数估计问题。本文算法框图如图1所示。
3.1 目标位置参数估计
在利用属性散射中心模型对散射体进行参数估计时,首先进行位置参数和其他参数的降耦合[8]。然而在大转角情况下,目标的相对转动会导致目标信号存在明显的方位距离耦合,使图像出现散焦,降低成像质量,导致无法获得准确的位置信息。所以引入极坐标格式算法,解除回波包络方位距离的耦合性,获取聚焦良好的图像帮助从粗成像结果中估计出需要的位置参数。
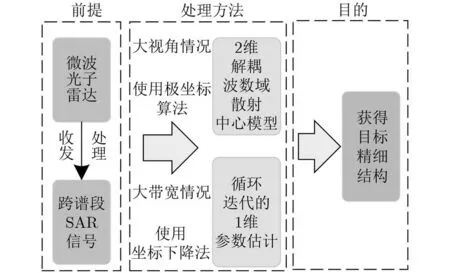
图1 算法框图
以目标上的某一点 Pn(x,y)为例,点目标的波数谱Sn为[16]

其中 KR为波束向量;rn=(x sin θ+y cos θ)为场景基准点到点目标 Pn的 距离向量;θ 表示目标转角的变化;σn为目标的回波振幅。大转角的情况下,耦合会产生散焦现象,降低图像的成像质量。PFA通过对波数域信号进行重采样实现转动补偿,将极坐标格式下的数据插值变换到直角坐标下,实现对距离和方位的解耦,然后使用2维FFT成像。
对波数谱回波式进行极坐标重采样,令Kx=KRcos θ,Ky=KRsin θ,代入到式(2)中得
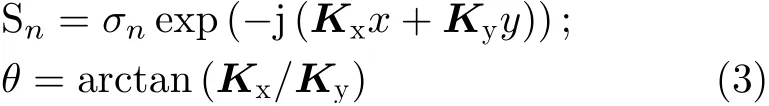
其中,θ 为重采样之后的转角,Kx为 方位向波数,Ky为距离向波数。得到较为清晰的成像结果后,从图像 中获取各个散射点的2维位置参数初始估计值。
3.2 2维解耦波数域散射中心模型
经过回波信号的两维波数域重采样,相应的属性散射中心表达式发生了变化。图2为2维极坐标插值示意图,传统的属性散射中心模型是在图2(a)极坐标格式下录取,数据收集范围为 fc·(1 −β/2)~fc·(1+β/2), 其中fc是中心频率,β 是相对带宽;角度在 −φm/2 ~φm/2之间变化。将数据由极坐标格式 (f,φ) 重新经插值变换到直角坐标格式(fx,fy)下,有: fx=f cos φ , fy=f sin φ,代入到原模型公式中有
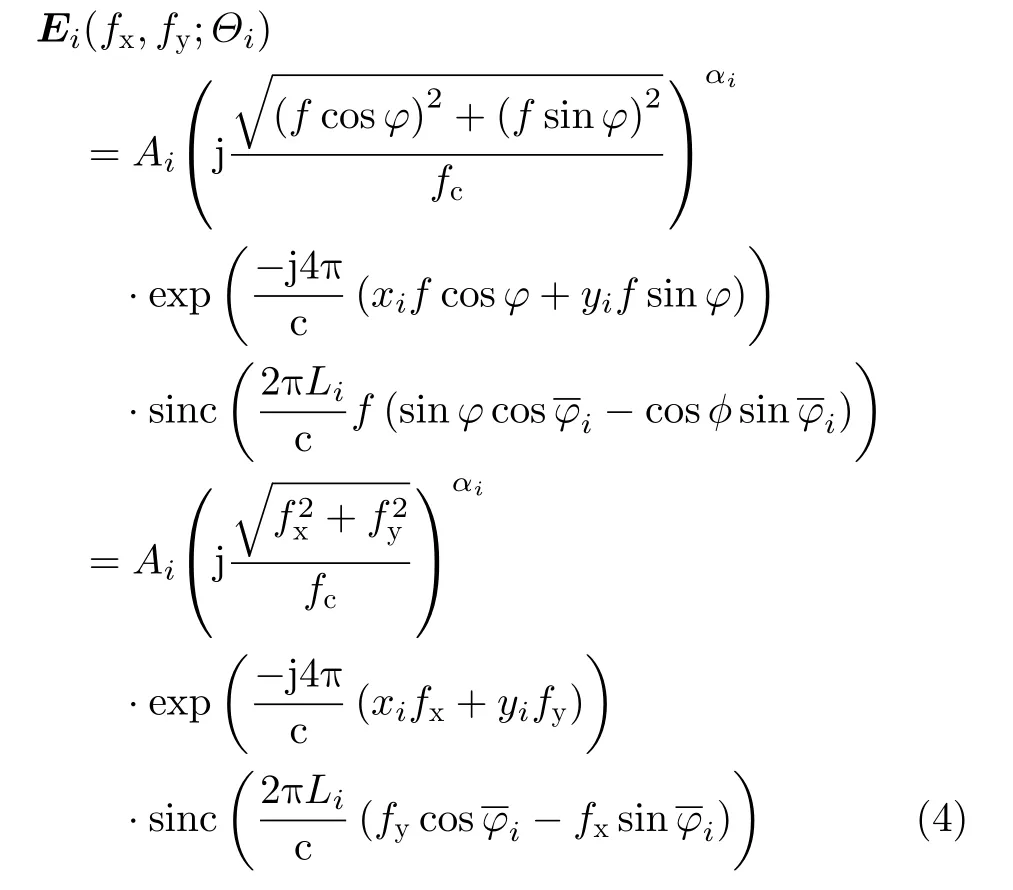

图2 2维极坐标插值示意图
3.3 参数{ L,φ,α}的估计 {}


3.4 幅度{ A}的估计

4 基于坐标下降法的属性散射中心估计流程
根据以上内容,本文所提算法步骤如下所示。算法流程图如图3所示。
步骤 1 利用极坐标算法对目标回波成像,从成像结果中估计位置参数x和y的大概位置。
步骤 2 将成像结果在图像域内采用分水岭算法进行图像分割,获得N个独立的属性散射中心。
步骤 3 将各子散射中心复图像变回数据域获得各属性散射中心的两维波数域数据。
步骤 4 根据2维解耦后的波数域属性散射中心模型公式构造字典。
步骤 5 利用本文所提基于坐标下降法的参数估计方法进行估计。
(1) 先固定 φ 和α 的值,在设定范围内搜索使P1达到最大的Li。如果估计的Li值为0,则跳过角度搜索,直接估计α 的估计值。

图3 参数估计算法流程图

(5) 符合精度要求后,用最小二乘法估计幅度Ai。
步骤 6 对所有散射中心重复以上步骤。
步骤 7 根据已得到的估计值识别各属性散射中心对应的散射体结构类型。

5 实验结果与分析
5.1 简单目标仿真实验分析
利用FEKO软件对模型回波进行仿真。圆柱体长为0.5 m,位置为[–0.25 m, 0 m];球体半径为0.01 m,位置为[–0.8 m, 0.4 m]。扫描频率为6~16 GHz,带宽为10 GHz,采样间隔为78 MHz;观测角度为[–26°, 26°],采样间隔为0.25°。按照图3的流程,首先使用传统算法对仿真模型成像结果如图4(a),图像散焦,无法辨别圆柱和球体。通过极坐标算法对目标模型插值变换得到成像如图4(b)所示,从图像中估计出圆柱体、球体的位置。之后利用分水岭算法在图像域进行图像分割,对分割后的图像作逆变换得到频率域数据。
使用本文方法估计参数,结果如表1所示。由参数重构的图像如图4(c)所示。
可以看出,散射中心1的长度估计误差约为0.05 m,位置估计误差均小于0.01 m,其它参数估计与真实值一致。
5.2 估计性能分析
为了分析本文方法的参数估计性能,在不同信噪比(Signal-to-Noise Ratio, SNR)情况下进行蒙特卡洛实验,雷达参数与5.1节的实验相同,信噪比变化范围为[ 0,20]dB,计算估计的散射中心的参数集与真实值的均方误差(Mean Square Error,MSE)以及均方根误差(Root Mean Square Error,RMSE)。
由图5可以看出,本文算法在SNR优于0 dB时可以获得较为准确的估计结果,且受到噪声的影响较小。而当SNR低于0 dB时,估计精度会明显下降。出现这种现象的原因是0 dB以上时图像分割的结果精度较高,可以获取精确散射中心位置和数据,另外噪声和单个目标数据的弱相关性使得所提方法估计精度较高,而当信噪比下降,图像分割结果误差变大,以上条件无法保证,故精度下降。另外由于分布式目标的参数较多,其估计的精度相比局域式要差。

表1 仿真模型参数估计结果
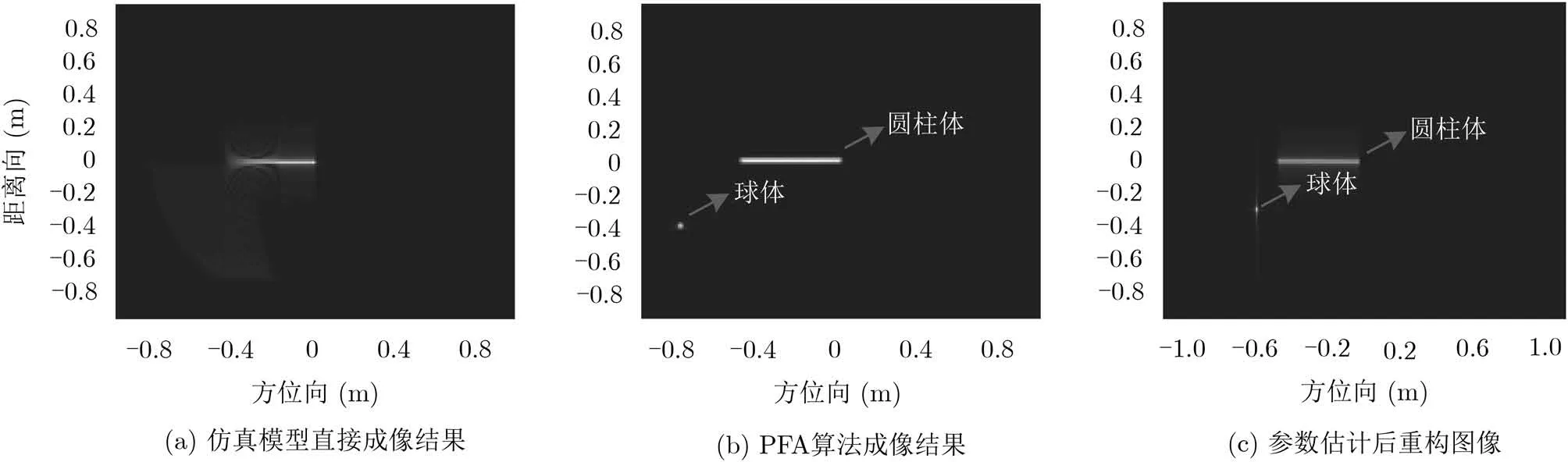
图4 仿真成像结果

图5 不同信噪比下散射中心参数估计情况
5.3 复杂目标仿真实验分析
下面使用Xpatch仿真的挖掘机数据进一步验证算法的有效性。数据扫描频率为7.0472~12.9528 GHz,采样间隔为11.5 MHz,带宽约为6 GHz,距离分辨率约为0.025 m。方位角变化范围为[–10°,9.9286°],采样间隔为0.0714°,方位分辨率约为0.03 m。
如图6(a)为传统成像结果,图像聚焦质量较差;图6(b)为经过极坐标重采样后的成像结果,聚焦良好;根据参数估计结果重构的图像如图6(c)所示。各个散射中心的参数估计值如表2所示。
由表2可知,图像的前部为直边,对应挖掘机的铲斗部分;铲斗两侧后部为圆柱,是挖掘机的连杆部分;图像的中部主要由角、球面及直边组成,为挖掘机机体连接部分;图像的后部由帽顶和直边组成,为挖掘机的工作室部分。

图6 挖掘机成像结果

表2 挖掘机散射中心参数估计结果
根据以上实验结果可以看出,通过本文所提方法可以比较高效、准确地识别目标的位置、长度以及形状。
6 结束语
针对跨谱段、大视角SAR目标的参数估计问题,本文首先利用极坐标算法进行成像,估计散射中心的位置参数。之后通过分水岭算法将图像分割成多个散射中心,再估计每个散射中心的电磁模型参数。考虑到构造字典维度高的问题,提出结合坐标下降法的参数估计方法,将高维参数估计问题转化成多个1维估计问题,再结合Hooke-Jeeves算法进一步提高参数估计精度,降低了运算量,并具有较高的准确性。根据各个散射中心的参数可以识别它们的结构及所处位置。通过对FEKO仿真模型及挖掘机模型的实验验证了方法的有效性。

