基于满意度分析的高速铁路列车运行调整优化研究

王艺楠，田 锐，王义惠，龙思慧，李 璇

（1.北京交通大学 交通运输学院，北京 100044；2.中国国家铁路集团有限公司 调度指挥中心，北京100844；3.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；4.中铁第五勘察设计院集团有限公司 线路运输设计研究院，北京 102627)

0 引言

高速铁路由固定设施、移动设备和运营控制系统组成。作为一种速度快、正点率高、可靠性强、经济环保的现代化出行方式，高速铁路列车在正常环境下按图行车，但在遇到由人员因素、自然环境因素、固定设施移动设备因素等带来的扰动时，会造成列车晚点、旅客出行满意度下降、铁路通过能力降低、运输效益下降。高速铁路列车调度的目标即是使列车运行尽快恢复到正常状态，降低性能损失。因此，研究扰动下的高速铁路列车运行调整理论具有重要意义。文中主要研究恶劣天气下的高速列车运行调整。

在列车计划编制与调整和多目标优化领域，孟令云等[1]提出了一种以改变到发时刻、改变次序、改变股道、改变路径为手段的同步优化列车时刻表和列车路径的精细化混合整数规划模型；周晓昭等[2]建立了高速铁路列车运行图智能调整模型；雷艳红[3]研究了不同大风预警提前时间和不同的风速预警值下广义费用最小的高速列车运行调整方案；孙少军等[4]建立了以晚点时间和晚点列数加权和为目标的城市轨道交通列车运行调整模型；章优仕等[5]研究了列车运行调整综合满意度目标体系；陈彦如等[6]研究了复线列车运行调整的满意优化问题；Keivan 等[7]用ε-约束法解决了旅客旅行时间最小和列车能耗最小的多目标优化问题。金炜东[8]提出了满意度函数的数学描述和公式描述(线性满意度)。满意优化方法通过设定直接影响目标综合满意度的满意度函数，使得指标的变化对目标值的影响更合理，更能准确地反映综合满意度与各单目标满意度的关系。

传统的调度模型目标函数多为单目标，如最小化总晚点时间或其绝对值、最小化总旅行时间或其绝对值等，或是不同目标直接加权，而不是将满意度加权。为了更加合理地评价列车运行，必须建立更为科学的列车运行调整模型。为提高调度工作的质量和旅客出行满意度，文中建立基于总晚点时间最小和晚点列数最小的列车运行调整混合整数规划模型，在此基础上提出基于满意优化的线性满意度加权、梯形满意度加权和传统多目标加权模型。

1 模型建立

1.1 问题描述

当由于恶劣天气需要临时限速时，分散自律调度集中系统(CTC)拟定临时限速命令控制列车限速运行。临时限速命令主要包含限速里程(起止范围)、限速值、限速时段等信息。为了研究临时限速下的最优列车运行调整计划，将路网抽象为微观行车资源，建立混合整数规划模型描述列车的运行状态。列车运行需要满足最早发车时间、最小运行时间、区段最小停留时间、安全时间间隔等约束条件，受限速影响的列车还要满足限速约束。将计划时刻表和限速信息作为输入，通过调整列车在各站到发时刻、运行径路和次序，就可以得到总晚点时间和晚点列数最小的列车运行调整计划。

1.2 约束条件

模型约束条件如下。

（1）流量平衡约束。该组约束表示列车在起点、终点和中间点的流量平衡。

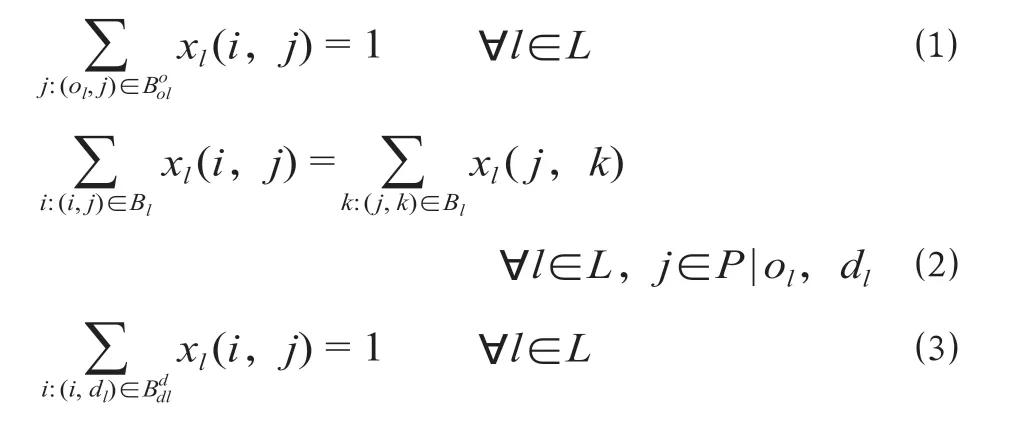
式中：l表示列车编号；L表示列车集合；i，j，k表示节点编号；P表示节点集合；ol/dl表示列车l的始发/终到节点；(i，j)、(j，k)表示区段；表示起始于节点ol的区段的集合；Bl表示列车l可能经过的区段集合；表示终止于节点dl的区段的集合；xl(i，j)是0-1 变量，如果列车l经过区段(i，j),则xl(i，j) = 1，否则xl(i，j) = 0；xl(j，k)同理。

（2）区段间转换约束。该约束表示2 个相邻区段的转换关系，即如果列车相继经过2 个连续区段，则列车离开前一区段的时间等于列车到达后一区段的时间。

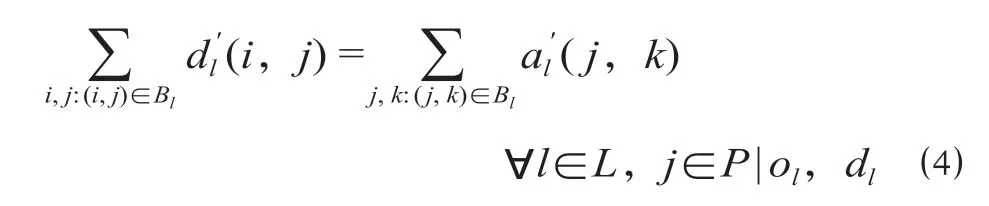
（3）时空网络映射约束。该组约束表示如果列车经过某区段，则它在该区段的到达、离开时间都大于0，反之等于0。

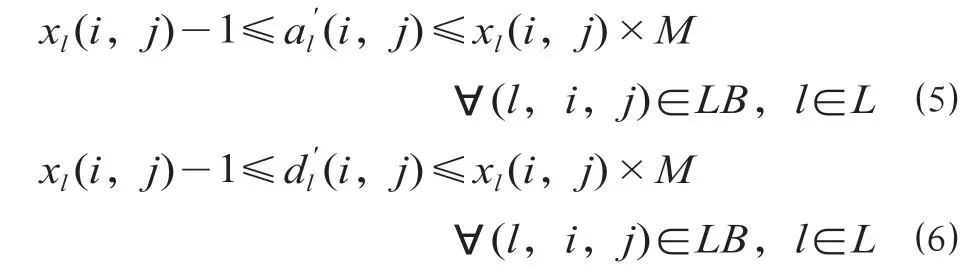
式中：(i，j)表示列车l实际离开区段(i，j)的时间；LB表示列车l和它可能经过的区段共同构成的集合；M表示一个充分大的数。

（4）离开时间窗约束。该约束表示列车离开起始站的时间不早于计划离开时间，即列车不能早发，保证按时刻表到达的旅客可以赶上列车。

式中：(ol，j)表示列车l可能经过的起始于起点的区段集合；表示列车l实际离开区段(ol，j)的时间；el表示列车l在起点的最早发车时间构成的集合。

（5）限速约束。临时限速下的列车运行示意图如图1 所示。其中黄色区域表示限速区域，位于限速区域2 个边界的运行线是不受限速影响的。列车在限速开始时间之前离开限速区域或在限速结束时间之后进入限速区域均不会受到限速的影响。因此，列车受限速影响的条件为列车在限速结束之前进入限速区域且在限速开始之后离开限速区域，用不等式 ⑻ 表示列车受限速影响的时空条件。引入变量表示列车是否受限速影响，得到限速约束 ⑾—⒂，又将约束 ⒂ 线性化处理转化为约束 ⒃—⒅。

图1 临时限速下的列车运行示意图Fig.1 Train operation diagram under temporary speed limit

式中：tl(i，j)表示列车l在区段(i，j)上的实际运行时间；LWB表示经过限速区域的列车l与限速区段(i，j)共同构成的集合；s(i，j)表示限速区段(i，j)上限速的开始时间；e(i，j)表示限速区段(i，j)上限速的结束时间；tl(i，j)表示列车l在区段(i，j)上的实际运行时间；αl(i，j)、βl(i，j)为引入的中间变量，当列车在临时限速开始后离开限速区域时，αl(i，j) = 1，反之，αl(i，j) = 0；当列车在限速结束前离开限速区域时，βl(i，j) = 1，反之，βl(i，j) = 0；o代表0.1；ηl(i，j)为限速表征变量，只有当αl(i，j)与βl(i，j)均为1 时，ηl(i，j)才为1，也就是该列车受限速的影响。

（6）运行时间约束。列车在非限速区段运行时，运行时间大于等于最小停留时间加计划运行时间。列车在限速区段运行时，如果受限速的影响，列车在限速区段的计划运行时间变为限速区段长度除以限速；如果不受临时限速的影响，列车实际运行时间的取值范围等同列车在非限速区段的实际运行时间取值范围。

式中：ltl(i，j)表示列车l 在区段(i，j)上的最小运行时间；ωlmin(i，j)表示列车l 在区段(i，j)上的最小停留时间；st (i，j)表示列车l 在限速区段(i，j)受到限速影响时的最小运行时间。

（7）能力约束。在同一区段上经过的相邻列车要满足安全间隔，这一安全间隔是前一列车离开区段与区段信号设备解锁和区段信号设备锁闭与列车到达区段的间隔时间总和。该组约束保证在同一时间同一区段上只有一列车占用。

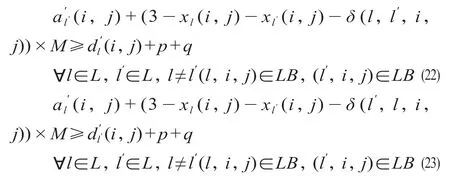
式中：δ (l，l"，i，j)和δ (l"，l，i，j)是区段占用顺序变量，如果列车l 比列车l"先到达区段(i，j)，则δ (l，l"，i，j) = 1，否则δ (l，l"，i，j) = 0；如果列车l"比列车l 先到达区段(i，j)，则δ (l"，l，i，j) = 1，否则δ (l"，l，i，j) = 0；p 表示列车占用某区段与到达该区段的时间间隔；q 表示列车离开某区段与释放该区段的时间间隔。

（8）晚点约束。如果列车实际到达时间小于或等于计划到达时间，则列车晚点时间为0；如果列车实际到达时间大于计划到达时间，则列车晚点时间为实际到达时间减计划到达时间。

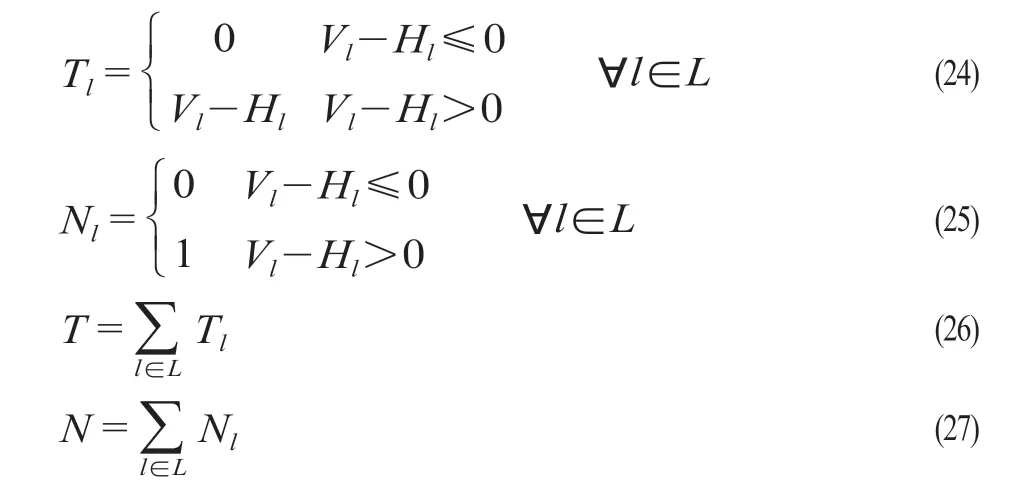
式中：Tl表示列车l 的晚点时间；Nl为晚点变量, 如果列车l 晚点，则Nl= 1，否则Nl= 0；T 为总晚点时间；N 为晚点列数；Vl表示列车l 实际到达终点dl的时间；Hl表示列车l 图定到达终点dl的时间。

（9）其他约束。为了更方便地描述列车实际到达终点站的时间，引入此约束。

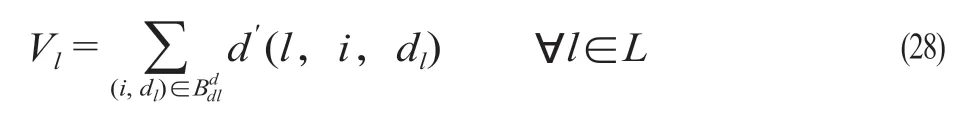
2 目标函数分析

2.1 线性满意度加权

满意优化方法包含了线性加权法的思想，是一种多目标优化方法，可以将多目标问题转化为单目标问题解决。

晚点列数和列车总晚点时间是相向变化的，若仅以总晚点时间作为目标函数，可能会为了减少晚点时间而增加晚点列数，降低正点率。只有将总晚点时间和晚点列数2 个指标综合考虑，才能更好地适应和反映实际中列车调整计划执行的满意情况。满意优化目标函数由总晚点时间和晚点列数2个指标构成，每个指标单独作为目标时都有对应的最优解和最劣解。

由于每个指标都是线性函数，因而依照线性插值建立独立满意度，并按照线性加权法形成综合满意度。

公式(29)表示总晚点时间的独立满意度，列车总晚点时间越短，满意度越高。

式中：Tmax，Tmin分别表示总晚点时间的最劣解和最优解；s1表示总晚点时间满意度。

公式(30)表示晚点列数的独立满意度，晚点列数越少，满意度越高。

式中：Nmax，Nmin分别表示晚点列数的最劣解、最优解；s2表示晚点列数满意度。

公式(31)表示综合满意度目标函数。

式中：s 表示列车延误的综合满意度；ω1表示总晚点时间的权重；ω2表示晚点列数的权重。

2.2 梯形满意度加权

以陈方南[9]提到的降半梯形满意度函数构造综合满意度。降半梯形满意度是常用的满意度函数之一，当指标在一定范围内满意度为1；当指标超过此范围而在另一范围之内时，满意度以线性的方式由1 逐渐降为0；当指标更大时，满意度为0。

公式(32)表示总晚点时间的独立满意度。

式中：a1表示梯形满意度中满意度为1 的最大总晚点时间；a2表示梯形满意度中满意度为0 的最小总晚点时间；s"1表示总晚点时间满意度。

公式(33)表示晚点列数的独立满意度。

式中：b1表示梯形满意度中满意度为1 的最大晚点列数；b2表示梯形满意度中满意度为0 的最小晚点列数；s"2表示晚点列数满意度。

公式(34)表示综合满意度。

式中：s"表示列车延误的综合满意度。

2.3 传统多目标加权

线性加权法是一种常见的多目标优化方法。线性加权同样存在满意解的情况。

公式(35)表示总晚点时间的独立满意度。

3 算例分析

3.1 场景搭建

设计单向调度区段进行仿真试验。该区段中运行列车共10 列。其中，动车组列车4 列，高速铁路列车6 列。

算例使用的路网拓扑图如图2 所示，共有125个节点。

原始时刻表的设计满足以下原则：①安全间隔至少为4 min；②经过某站的车一定在该站的正线通过，在某站停站的车一定在该站的到发线通过；③车站到发线的数量满足在该站同时停车的列车数量要求。

设计一个临时限速场景，恶劣天气导致的临时限速场景设计如表1 所示。

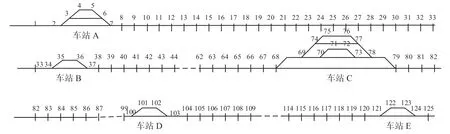
图2 路网拓扑图Fig.2 Railway network topology

3.2 计算结果

总晚点时间和晚点列数的最优解和最劣解如表2 所示。

线性满意度线性加权和传统多目标加权计算结果如表3所示，通过改变权重，得到了一组非劣解。

线性满意度和传统多目标线性加权模型总晚点时间与晚点列数的帕累托关系图如图3 所示，从图3 中可以看出，随着晚点列数权重的减少，晚点列数增加，总晚点时间减小。满意优化的帕累托前沿优于线性加权的帕累托前沿。权重为0.5 的不同梯形满意度线性加权构造方法计算结果如表4 所示。综合表3 和表4，可以看出权重为0.5 时梯形满意度线性加权方法的计算时间优于权重为0.5 时传统多目标线性加权方法。

晚点列数最小、总延误最大的调整后运行图如图4 所示。从图4 中可以看出，临时限速导致G3，G5，G6 共3 列列车晚点，分别晚点3 113 s，2 140 s，1 289 s。临时限速直接影响D3，G3，D4，G5，G6 共5 列列车，间接影响D2。在B 站，D3 和G3 的发车顺序交换；在C 站，D4 和G5 的发车顺序交换；在D站，D2和G3的发车顺序交换，D4 和G6 的发车顺序交换。总延误最小、晚点列数最大的调整后运行图如图5 所示。

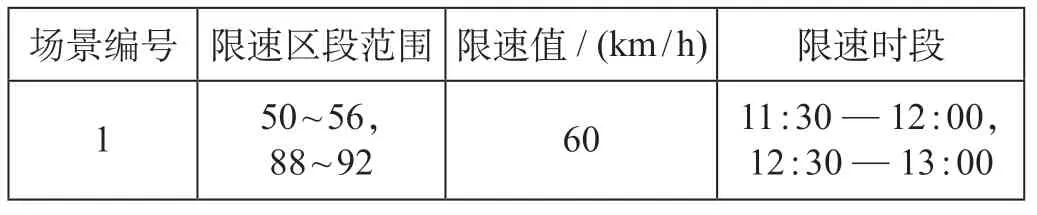
表1 恶劣天气导致的临时限速场景设计Tab.1 Scenario design of temporary speed limit caused by bad weather

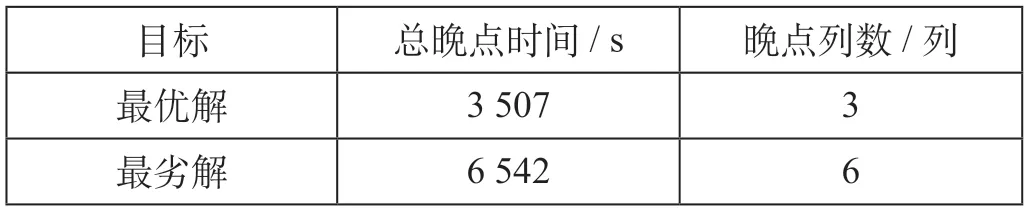
表2 总晚点时间和晚点列数的最优解和最劣解Tab.2 The optimal solution and the inferior solution of the total late time and the number of late trains

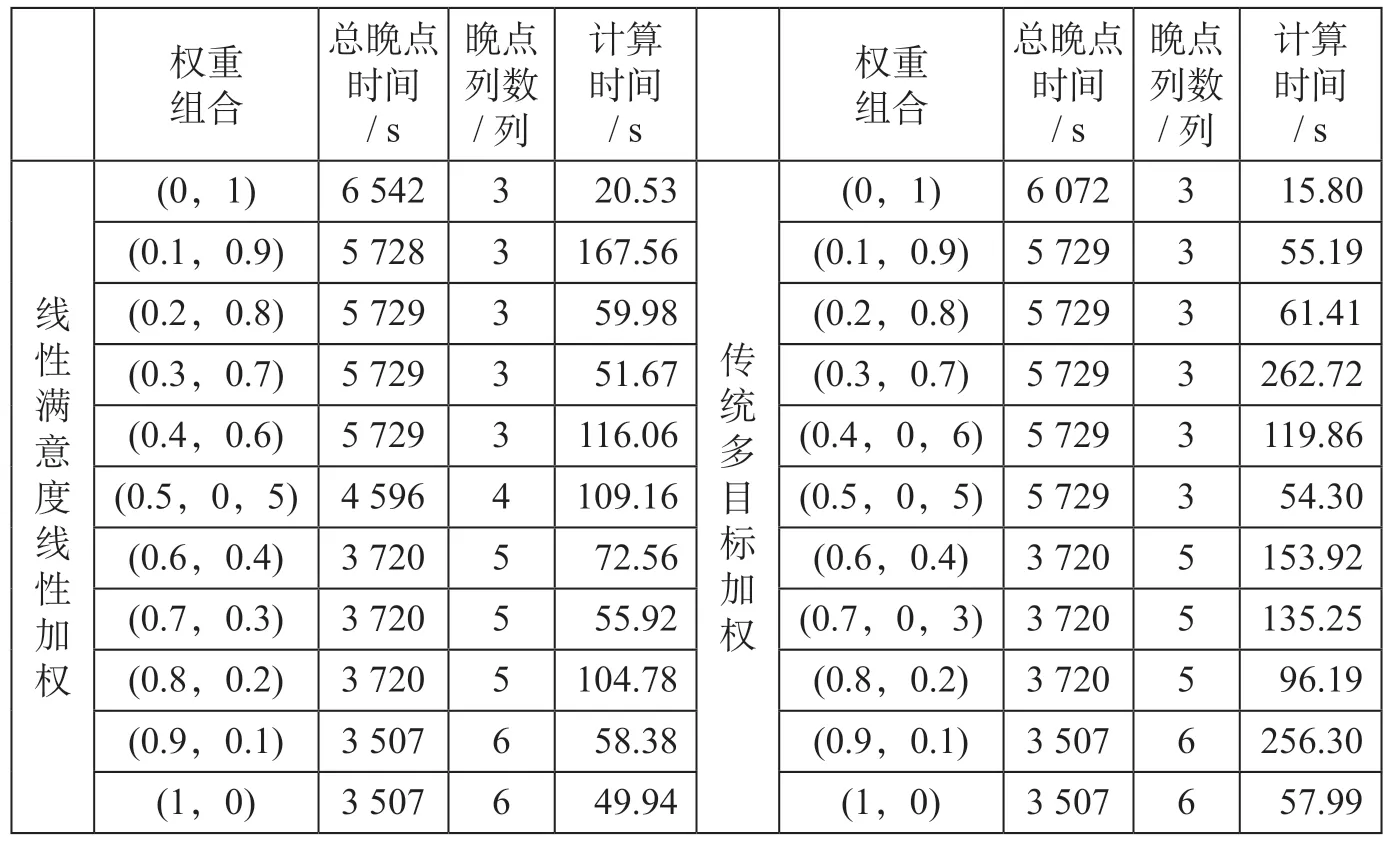
表3 线性满意度线性加权和传统多目标加权计算结果Tab.3 Linear satisfaction with linear weighting and traditional multi-objective weighting calculation results

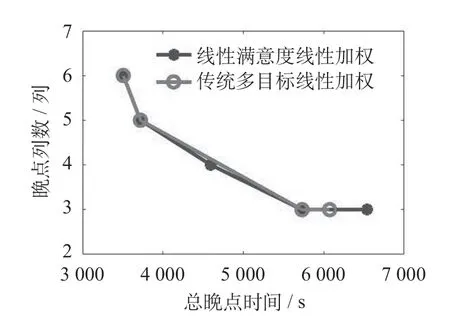
图3 线性满意度和传统多目标线性加权模型总晚点时间与晚点列数的帕累托关系图Fig.3 The Pareto diagram between the total late time and the number of late trains in linear satisfaction and traditional multi-objective linear weighted models

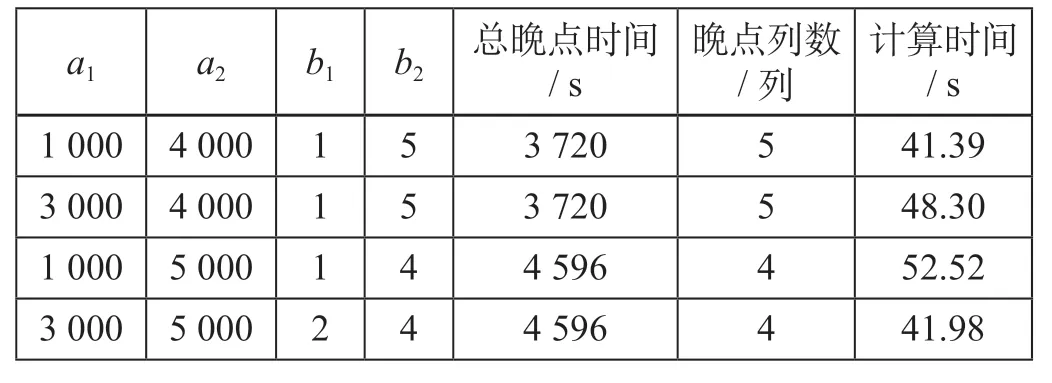
表4 权重为0.5 的不同梯形满意度线性加权构造方法计算结果Tab.4 Calculated results of different trapezoidal satisfaction linear weighted construction method with weight of 0.5

从图5 中可以看出，临时限速导致D3，G3，D4，G4，G5，G6 共6 列列车晚点，各晚点350 s，560 s，785 s，387 s，1 138 s，287 s。临时限速直接影响D3，G3，D4，G5，G6 共5 列列车，间接影响D2。在B 站，D3 和G3 的发车顺序交换；在C 站，D4 和G6 的发车顺序交换；在D 站，D2 和G3 的发车顺序交换。

综上，综合3 种列车运行调整满意优化模型的计算结果，采用满意度线性加权模型比传统线性加权模型具有更好的计算结果和更短的计算时间，可以满足临时限速下列车运行调整的实时性和有效性的要求，与预期相符。

4 结束语

面对复杂环境中的列车运行调整问题，结合实际运行情况和列车运行调整中各约束条件特点，从旅客出行服务品质和铁路系统运营效能等2 个主要角度出发，选用列车总延误、晚点列数2 个性能指标，对指标进行满意度分析，建立列车运行调整方案的综合延误满意度函数，通过满意度函数及综合满意度函数来对性能评价指标进行满意评价，以综合延误满意度最大为目标，分别建立了线性满意度加权模型、梯形满意度线性加权模型和传统多目标加权列车运行调整模型，通过一个仿真实例场景验证了文中提出的满意度线性加权模型在计算结果和计算时间上的优势，可以满足调度的实时性要求。相比于传统加权模型，满意度线性加权模型以函数刻画满意度，使满意度与相应指标具有更具体的映射关系，而多目标满意优化模型也可以更加适用于评价列车运行，为列车运行实时调整问题的求解提供一种新的思路和方法。

图4 晚点列数最小、总延误最大的调整后运行图Fig.4 The adjusted train diagram with the minimum number of late trains and the maximum total delay

图5 总延误最小、晚点列数最大的调整后运行图Fig.5 The adjusted train diagram with the maximum number of late trains and the minimum total delay