基于数值模拟的GH536高温合金铣削力模型
刘 东 王洪健
(北方工业大学机械与材料工程学院,北京 100144)
文 摘 为了研究GH536高温合金的铣削力来指导生产,利用DEFORM-3D对GH536的铣削过程进行了建模和仿真;设计铣削正交仿真方案,对仿真结果进行极差分析。结果表明:铣削深度、铣削宽度和每齿进给量对Fx、Fy和Fz均成正相关、而铣削速度对Fz正相关,其余负相关,其中铣削深度对铣削力影响程度最大,而铣削速度影响程度最小;利用SPSS 对正交仿真数据进行处理,建立GH536 铣削力预测模型,并对模型进行回归分析;设计铣削测力试验,将其结果与铣削力预测模型进行对比,并用铣削力理论模型求解结果作为参照对比,结果表明铣削力预测模型能够比理论模型更准确的预测GH536切削过程中的铣削力。
0 引言
高温合金是一种可以在600 ℃以上的高温环境中长期工作的合金,具有优秀的高温强度。高温合金按着基体元素种类可以分为:铁基高温合金、镍基高温合金和钴基高温合金。而GH536是一种含铁量较高的固溶强化型的镍基高温合金材料,其相似牌号有HastelloyX(美国)、NC22FeD(法国)、NiCr22 FeMo(德国)、Nimonic PE13(英国)。GH536 具有较强的抗氧化、抗腐蚀性,在900 ℃以下仍然具有中等的持久和蠕变强度,而且该合金在650~980 ℃长期使用后具有一定的时效硬化现象[1],是一种工业性能极其优秀的镍基高温合金.然而高温合金普遍为难加工合金,GH536 自然也不例外,加工过程中切削力大、切削温度高,使得刀具磨损严重[2]。GH536 的加工性能差在某些程度上抑制了GH536 的推广和使用。所以对GH536 的加工过程进行研究十分重要,文献[3]对GH536 铣削加工的表面粗糙度进行了研究,通过正交实验建立了GH536 铣削参数与加工表面粗糙度的预测模型。文献[4]研究了对GH536 使用电火花磨削加工技术。目前对于GH536的铣削加工研究较少,尤其在铣削力方面。
随着计算技术的发展,对于铣削加工过程的研究已经由以前的实验法、理论法变成使用有限元仿真软件来进行研究,极大地减少了研究成本和研究时间。文献[5]利用DEFORM对GH4169合金进行铣削仿真,研究了铣削参数对铣削力的影响。文献[6]使用DEFORM 软件对7075 铝合金进行车削仿真,并建立了车削力预测模型。本文使用有限元软件DEFORM 建立GH536 的铣削有限元模型,对GH536进行铣削力分析并建立铣削力预测模型。
1 铣削参数的选择及铣削模型的建立
1.1 铣削参数的选择
仿真刀具选用直径4 mm,前角5°,后角9°,螺旋角35°的硬质合金钨钢铣刀。铣削参数方案选用四因素三水平正交实验表,对于硬质合金铣刀铣削镍基高温合金其铣削速度一般不超过15~30 m/min[7],由于加工硬化现象每齿进给量不宜过小,故设计因素水平表如表1所示。
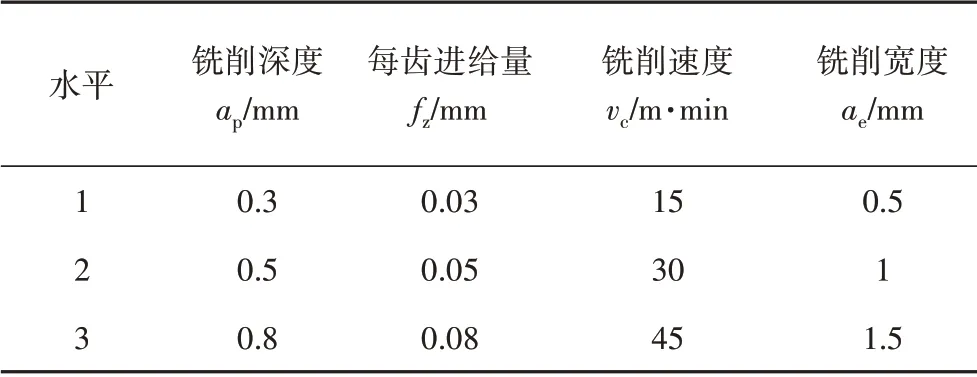
表1 因素水平表Tab.1 Factor level table
1.2 几何模型的建立及网格划分
使用Solidworks 三维建模软件对铣刀和工件进行建模,保存为STL 格式导入到DEFORM 中。其中刀具为简化模型减少仿真时间只建模铣刀刀头部分,其高度为2 mm。工件建模为直径6 mm 高度1 mm 的圆柱体,并根据铣削宽度确定模型宽度,为省去部分铣刀切入过程,于上表面切除铣刀直径为直径、铣削深度为深度的圆槽,如图1所示。在切削过程中工件会产生变形、分离,所以工件定义为塑性,而刀具的变形可以忽略不计,因此将刀具定义为刚性。
在DEFORM 中划分网格时有两种网格划分方式:四面体网格、六面体网格。六面体网格相对于四面体网格的仿真结果更加精确但是难以绘制出复杂模型的边界形状,在切削过程中产生的切屑是一种复杂边界形状模型,使用六面体网格难以完美实现其形状,而切屑的形状是否符合实际切削过程不影响仿真结果的准确程度,故本次仿真采用四面体网格划分方式。网格尺寸最小值应该小于最小特征量才能产生切屑,而一般取30%来保证仿真的精确度。对工件划分网格数目为50 000,最小网格尺寸为0.006 mm,小于铣削过程中最小特征量0.03 mm 的30%。刀具的网格数目对仿真结果的影响不大,因此对刀具网格划分15 000 并对刀尖进行局部加密,如图2所示。

图1 工件建模与网格划分Fig.1 Workpiece modeling and grid generation

图2 铣刀建模与网格划分Fig.2 Milling cutter modeling and mesh generation
1.3 铣削模型的设置
1.3.1 本构方程
本构方程选用常用的Johnson-Cook 本构方程,J-C 方程是一种经验方程,其参数获取简单可通过实验获取,因此是目前研究切削仿真的主要本构方程:

式中,A、B、n、C、m为材料参数,ε*为无量纲应变率,ε*=-εp/ε0,为有效塑性应变率,ε0为参考塑性应变率,一般取ε0=1 s-1,T*=为无量纲温度;Tr为室温,Tm为熔点。GH536的J-C模型参数如表2所示。

表2 GH536的J-C模型参数[8]Tab.2 J-C model parameters of GH536
1.3.2 边界条件
在DEFORM 中需要对工作环境、接触条件进行设定。仿真工作环境为室温20 ℃,冷却方式为空冷。接触的摩擦模型选用剪切摩擦模型,摩擦因数为0.6。
1.3.3 分离准则
为了在仿真中产生切屑需要设置切屑分离准则,本次仿真选用DEFORM 中默认的分离准则,即节点压力大于0.1 MPa节点分离。
1.3.4 断裂准则
为了使切屑的形成更加符合实际加工过程,需要设置材料的断裂准则。本次仿真选择Nomalized Cockcroft & Latham 准则,其值通过实验获取。NCL断裂准则对切削力和断裂面的实现上具有较强的准确性、稳定性[9]。
2 铣削力预测模型建立
2.1 正交仿真结果
根据因素水平表设置的正交仿真方案及其结果如表3所示。
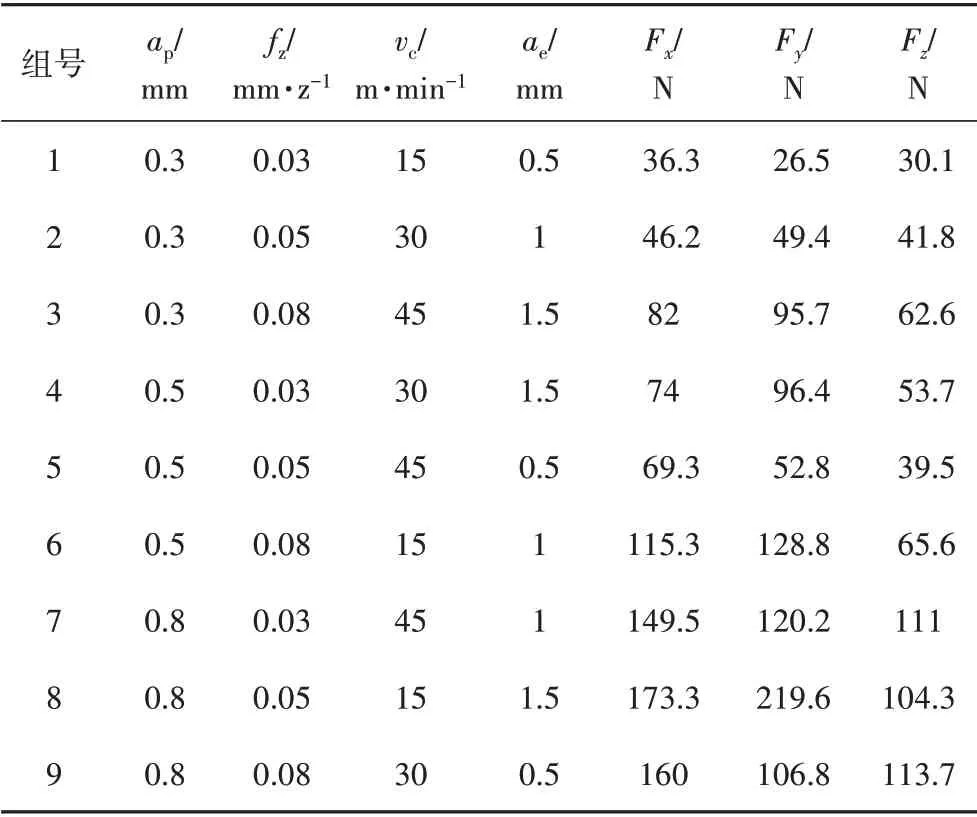
表3 正交仿真方案及其结果Tab.3 Orthogonal simulation scheme and results
2.2 数据处理与分析
极差分析可以分析出各铣削要素对三个不同方向铣削力的影响趋势和程度。铣削力越大对刀具的磨损越大,因此对于铣削参数的选择往往是铣削力越小越好,从这方面可以选择最佳铣削参数组合。如表4所示,以进给抗力Fx为例可以看出,ap、fz、ae对Fx正相关,Vc对Fx负相关,影响程度顺序为ap>fz>ae>vc根据不同水平的不同铣削力可以得出最优组合为A1B1C2D1。
同志们,宪法的根基在于人民发自内心的拥护,宪法的伟力在于人民出自真诚的信仰。我们要按照中央部署要求和省委工作安排,深入推进科学立法、严格执法、公正司法、全民守法,坚持有法可依、有法必依、执法必严、违法必究,推动宪法实施真正成为全体人民的自觉行动,更好发挥宪法作为国家根本法的引领、规范、推动、保障作用,为新时代推进全面依法治国、建设社会主义法治国家作出积极贡献。
同理来分析Fy和Fz:ap、fz、ae对Fy正相关,Vc对Fy负相关,影响程度顺序为ap>ae>vc>fz,最优组合为A1B1C2D1。ap、fz、ae、Vc对Fz正相关,影响程度顺序为ap>fz>ae>vc,最优组合为A1B2C1D1。
2.3 铣削力预测模型
为了描述铣削力与铣削因素之间的复杂关系,常用指数函数公式作为铣削力的预测模型:

表4 Fx极差分析Tab.4 Fx range analysis

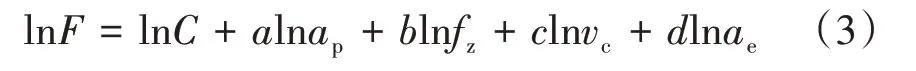
将两边取对数之后:即可将多元非线性回归方程转化为多元线性回归方程,对上式进行最小二乘法处理后即可得到参数a、b、c、d。将仿真值带入到SPSS中进行回归处理,得到回归方程即为铣削力预测模型,其结果如下:
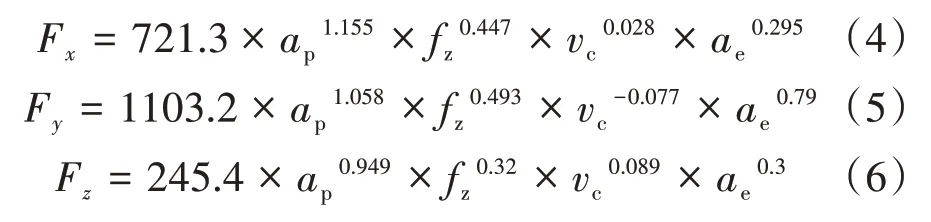
2.4 铣削力预测模型回归分析
SPSS 自带对回归方程验证分析的功能,其验证结果如表5所示。

表5 回归方程验证分析Tab.5 Regression equation validation analysis
从结果中可以看出x、y、z三个方向的相关系数R均在0.8~1区间,表明在三个方向上变量之间全部具有较高的线性关系,判定系数R2全部接近1,表明在三个方向上回归方程拟合程度较高。统计量F通过查表可知F0.01(4,4)=15.977,F0.05(4,4)=6.388,从表中可以看出在x、y方向 统计量F远大于F0.01(4,4),概率值P小于0.01,因此判定x、y方向上的回归方程线性回归效果高度显著;在z方向F值大于F0.05(4,4),概率值P小于0.05,因此判定z方向上的回归方程线性回归效果较为显著。
3 预测模型的验证
为了验证铣削力预测模型对铣削力的预测水平,设计铣削力测力实验,并将相同铣削参数带入到预测模型中进行求解,然后将其结果与铣削实验结果进行对比。为了对比预测模型与理论模型的优劣,同时使用铣削力理论模型对其进行求解作为参照对比。
3.1 铣削力测力实验方案
为了验证预测模型,在仿真中铣削参数范围内选取几组参数,设计一组铣削测力试验。如表6所示。
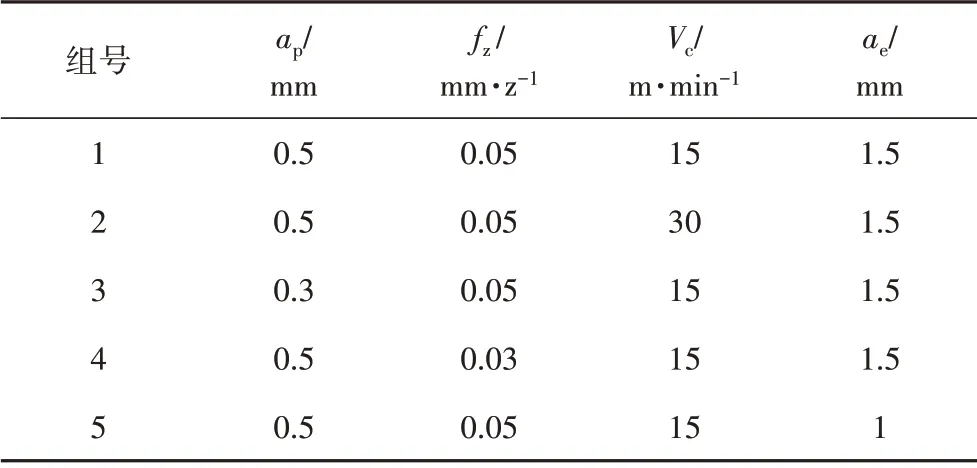
表6 铣削实验方案Tab.6 Milling experiment scheme
3.2 实验验证
铣削实验平台由以下设备组成:4 mm 直径4 刃AlTiN 涂层钨钢硬质合金立铣刀,前角5°,后角8°,螺旋角35°;铣床采用MCV1000 数控铣床,最大转速为6 000 r/min;测力仪传感器采用Kistler 生产的9027 C三向石英压力传感器;采集器使用北京东方所生产的INV306U 智能信号采集处理分析仪以及信号放大器和计算机等设备。
3.3 铣削力理论模型
根据文献[10]所提出的理论模型对GH536 的铣削过程进行了理论计算,该文献中将铣削力数值化为切削力系数与瞬时切削面积的乘积,对于螺旋铣刀铣削面积需要进行微分求解,因此该理论模型的基本公式为:
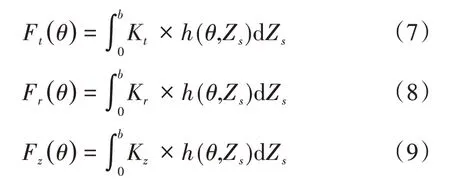
式中,Ft(θ)为瞬时切向铣削力,Fr(θ)为瞬时径向铣削力,Fz(θ)为瞬时轴向铣削力,Zs为铣刀轴线上任意一点距离铣刀底面中心的距离,h(θ)为瞬时切削厚度,Kt、Kr和Kz为切向、径向、轴向切削力系数,可用Armarego 经典模型求解。求得结果可通过以下公式转换成直角坐标系:

3.4 验证结果
对比结果如表7所示。

表7 验证对比结果Tab.7 Verifies the comparison results
从表中数据可以看出,铣削力预测模型计算结果与铣削实验结果对比在Fx方向上平均误差为18.7%,Fy方向上最高误差为12.52%,Fz方向上平均误差为9.14%,单项最高误差为36.6%。表中部分x、z向误差相对较大,分析原因可能为铣削实验中刀具受进给力产生的弯曲和震动、铣床工作台工作时产生的震动以及预测模型对正交仿真结果的拟合误差累计产生,但从整体来看绝大部分误差都在10%左右,说明该铣削力预测模型能够较为准确的预测铣削力数值。
铣削力理论模型结果与铣削实验结果对比在Fx方向上平均误差为62.28%,Fy方向上平均误差为38.32%,Fz方向上平均误差为71.58%,单项最高误差为78.9%,从整体来看大部分误差都在50%左右。误差比较大的原因分析如下:理论模型是一种将复杂铣削过程化为简单理论公式计算的模型,在简化过程中忽略铣削过程中的许多实际工况,不能完全真实的反映实际的铣削工况。其次不同的金属特性对于理论模型的建立具有一定的影响,而GH536 属于一种较为新型的镍基高温合金,对于这种材料切削过程的理论计算分析还有待进一步研究深入。
综上所述,实验获取的铣削力预测模型相比于常规的切削理论模型在对于铣削GH536的铣削力预测上具有更小的误差,能比较准确的预测GH536 切削过程中的铣削力。
4 结论
(1)在DEFORM 中建立GH536 高温合金铣削力仿真模型,并设计4 因素3 水平正交仿真方案,获得进给抗力Fx、主切削力Fy、轴向抗力Fz。
(2)对铣削仿真结果做极差分析表明:x方向铣削力与ap、ae、fz成正相关,与vc呈负相关,影响程度ap>fz>ae>vc,最佳组合为铣削深度0.3 mm、每齿进给量0.03 mm/z、铣削速度30 m/min,铣削宽度0.5 mm;y方向铣削力与ap、ae、fz成正相关,与vc呈负相关,影响程度ap>ae>vc>fz,最佳组合为铣削深度0.3 mm、每齿进给量0.03 mm/z、铣削速度30 m/min,铣削宽度0.5 mm;z方向铣削力与ap、ae、fz、vc均成正相关,影响程度ap>fz>ae>vc,最佳组合为铣削深度0.3 mm、每齿进给量0.05 mm/z、铣削速度15 m/min,铣削宽度0.5 mm。在实际生产中应与铣削质量、生产效率等相结合选择加工参数。
(3)使用GH536 正交仿真结果建立GH536 高温合金的铣削力预测模型,并且进行回归分析。
(4)设计铣削力测力试验,将其结果与铣削力预测模型进行对比,并使用理论模型求解结果作为参照对比,结果表明本文建立的预测模型比理论模型更能准确的对铣削力进行预测。

