计算机博弈算法在黑白棋中的应用

摘  要：计算机博弈是人工智能的重要分支之一，文章对人工智能算法黑白棋中的应用进行了研究。首先介绍了计算机博弈中的经典黑白棋算法，然后介绍深度强化学习中两种典型的时间差分算法的定义和实现过程，以及两者的区别和联系。最后评测蒙特卡洛树搜索算法、Q学习算法和SARSA算法三种算法在黑白棋实际应用的表现，以及后续改进的方向。

关键词：蒙特卡洛树搜索;深度强化学习;马尔科夫决策过程;Q学习;SARSA

中图分类号：TP181    文献标识码：A 文章编号：2096-4706（2021）17-0073-06

Abstract： Computer game is one of the important branches of artificial intelligence. This paper studies the application of artificial intelligence algorithm in black and white chess. This paper first introduces the classical black and white chess algorithm in computer game， and then introduces the definition and implementation process of two typical time difference algorithms in deep reinforcement learning， as well as their differences and relations. Finally， evaluate the performance of MCTS algorithm， Q learning algorithm and SARSA algorithm in the practical application of black and white chess， as well as the direction of subsequent improvement.

Keywords： MCTS; deep reinforcement learning; Markov decision process; Q learning; SARSA

0  引  言

计算机博弈是人工智能的分支领域之一。它结合了计算机算法与博弈论，成为人工智能算法应用在其他领域前的最佳验证领域，被誉为是人工智能的果蝇[1]。传统的计算机博弈算法一般基于树搜索算法。它是一种穷举算法，采用深度优先的方式搜索整棵多叉树。假定树的分支（也称为宽度）是w，深度是d，那么它的时间复杂度为wd。指数级别的复杂度在实践中由于计算结果的时间可能达到好几天甚至好几个月，很难得到应用。

科学家针对如何在宽度和深度这两方面去减少搜索时间这一问题提出了很多有效的解决方案。第一种是减少搜索宽度。信息论之父香农（Claude shannon）于1950年提出的策略为有选择性地遍历树的分支。它可以显著地减少搜索次数，副作用是会丢失有效的分支路线。

1958年Newell等提出了一种可有效减少搜索宽度的算法：α-β剪枝（alpha-beta pruning）算法。相比香农教授的随机选择分支算法，α-β剪枝算法是一种无损选择算法。

第二种有效减少搜索深度。普遍采用的策略是棋局评估函数。所谓评估函数就是一种判断当面局面哪一方领先以及具体领先多少的函数[2]。

这两项技术的组合成为了计算机博弈游戏人工智能的两大支柱。在目前计算机围棋的最强者、谷歌旗下开发的软件产品AlphaGo在下棋时就配置两台计算机，一台用于α-β剪枝，一台用于棋局评估。

计算机博弈应用于黑白棋早在1970年由日本学者开发出来。经过几十年的发展，目前最好的计算机黑白棋程序以WZebra等软件为代表。它们基于对游戏的透彻分析，精心打造了一套高水平的规则，采用非常复杂的搜索技术。 这些程序通常结合使用了强大的经过专家标记过的游戏数据集的来学习和进化。之前主流的棋局评估函数多采用静态评估的方式。直到1990年的计算机黑白棋世界冠军BILL3.0问世。它由当时在卡内基梅隆大学的李开复等开发，它开创性地采用了基于贝叶斯方法的动态评估函数，使得BILL3.0棋力成为当时的世界冠军[3]。

本论文介绍将深度学习和强化学习相结合的棋局評估函数，主要的策略是通过分析并优化评估函数参数，从而减少搜索深度，提高计算机对整体局面的判断力，从而在更短的单位时间内做出更有效的决策。

1  黑白棋简介

黑白棋又称奥赛罗棋。它是一种对弈的棋类游戏。采用类似于围棋的棋盘和棋子。棋盘大小为8行8列。棋子分为黑白两色，黑棋先走，棋子放在方格中，轮流走子，每次走子都必须要俘虏并翻转对方的棋子成为自己方棋子（简称吃子），如果轮到己方时，但是没有能吃子的落子点，则要弃权一次。双方都没有落子点时则游戏结束。最后以占据地盘多者为胜。

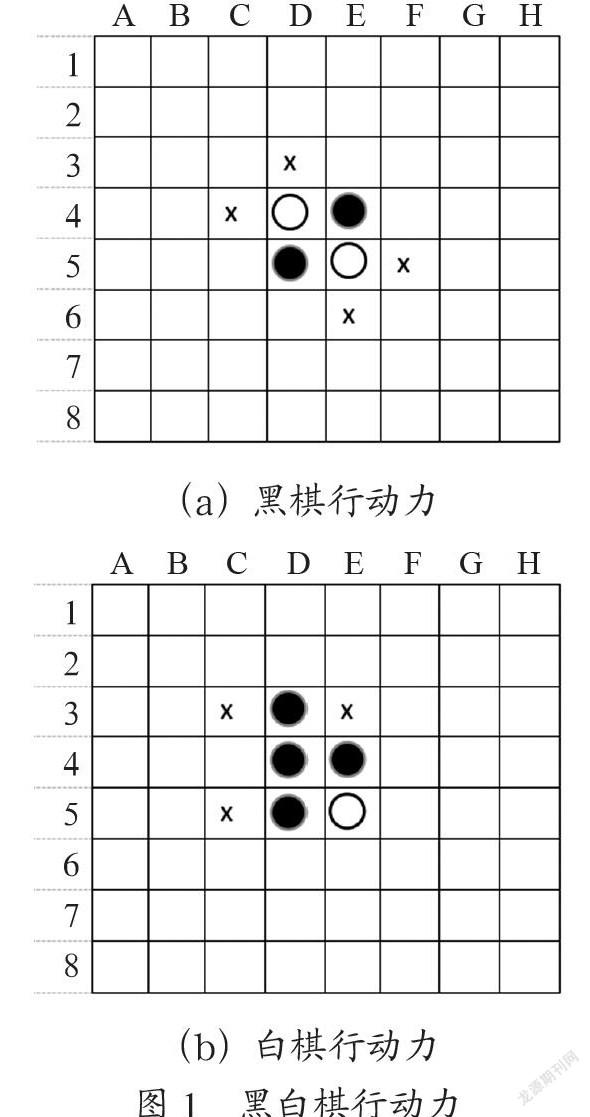
俘虏对方棋子规则是指对方棋子被自己的另外一个棋子同一条线之间的所有棋子都被俘虏并翻转成为自己的棋子。图1为起始棋局，X点为黑棋下一步合法的可选落子点，在黑白棋中称为行动力。

图1（b）图为黑子下在了d3位置后，d4位置的白棋变成了黑棋，因为d3和d5的黑棋连成了一条线。这个连线中间可以间隔1个或者多个对方的连续棋子，不能有空位。

2  经典黑白棋算法

由于黑白棋的规则简单，算法复杂度中等，它一直是计算机科学家在人工智能算法中钟爱的研究对象，研究流行度仅次于国际象棋。计算机黑白棋程序中常见的算法是树搜索算法。

2.1  树搜索算法

树搜索算法是一类计算机中常用的搜索策略，它们采用循环遍历可能的决策路径，并找出最佳的决策路线，其中有几种比较适合在博弈类游戏中应用。首先就是一种称为极小极大搜索算法（minimax search algorithm， MIN/MAX）。极小极大搜索算法是在对弈过程中假定对手和我们一样聪明，采用的策略总是使己方利益最大化，反之对手利益最小化。该算法非常适合于信息透明的零和游戏。黑白棋的最终目标是在64个棋盘格子中尽可能使己方棋子数量最大。所以黑白棋可以应用极小极大搜索算法。当我们采用某种最优策略，假定对手也采用最优的策略去应对。对于黑白棋类游戏，会产生相应的游戏树。树是具有宽度和深度的二维结构。宽度表示当前回合中可下的位置，深度表示当前回合某个可能选择到最终的游戏状态的回合数量。并且每一个回合宽度（用w表示）和深度（用d表示）都是会变化的。游戏中可能对局的数量可以用公式wd来表示。其中的宽度和深度都是平均值。根据黑白棋规则限定，每个落子点都必须要吃子，那么它的平均每回合宽度在一个合理的范围，有研究表明，黑白棋到中盘后平均宽度w约为10[4]。一局棋最多需要32回合结束，预估此树搜索的最大尺寸1032。而在实际运行中根据不同的计算精度需要，采用三个深度级别，分别为最小、中等和最大。最小一般预估6步可以达到较合理的结果。中等深度为12步，最大平均深度约为24步。如表1所示，以每秒1千万个局面的速度进行计算，仅仅计算中等深度每步需要花费166分钟，没有实战价值。由此必须要采用更加有效的搜索算法来进行优化。消除树的部分分支，这种方式称为剪枝。最有名的剪枝算法称为α-β剪枝算法。

2.2  α-β剪枝算法

采用α-β剪枝算法，可以显著减少搜索次数，研究表明中盘向前搜索12步，平均每步棋的次数为1亿数量级，耗时约10秒。如果减少为搜索10步，则在1秒内可以完成搜索。

α-β剪枝算法是基于极小极大化算法（MIN/MAX算法），通过优化来减少不必要搜索的剪枝方案，它是一种无损选择算法。α-β剪枝算法在规模较大的搜索树中效果非常显著，以井字棋游戏为例，从开局到终局进行搜索，生成的节点数量如表2所示[5]。从表2可以看出，采用α-β剪枝算法产生的节点数量约为仅仅使用MIN/MAX算法的1/15，采用优化算法后会有更大的提升。

2.3  棋局评估函数

棋局评估函数是根据当前的局面来进行评估每一个备选位置的价值函数。图2为wZebra软件提供的评估结果。其中图2（a）为开局。（D3，C4，F5，E6）四个备选位置价值相同。图2（b）为对白棋的下一步评估F4为-6表示负面结果，如果白下F4，则会对对手黑棋有利，黑棋得利为6，如图2（c）所示。白棋最佳的选择是从D6和F6任选一处。

评估函数的定义成为要解决的重点。首先采用专家法，根据世界顶级人类黑白棋棋手的总结，常见的评估和判断局面的几个变量为：

（1）行动力（MOBILITY）：由于黑白棋的规则要求每一步都必须吃掉对方的至少1个子，否则弃权1次。所以当前可选的位置是很容易计算的。图2中3个局面的行动力就分别是4（黑棋），3（白棋），5（黑棋）。

（2）潜在行动力（Potential MOBILITY）：所谓潜在行动力是指紧邻对手的空白位置的数量。图2中3个局面的潜在行动力就分别是10（黑棋），13（白棋），9（黑棋）。潜在行动力可能转换成行动力，并且包含了所有的行动力。它的影响因子要小于行动力。

（3）稳定子与边缘子：首先是稳定子的概念。位于角的棋子不可能被翻转，因为它永远也不会被对手的两个棋子夹住，那么四个角就是典型的稳定子[6]。除此之外，一旦有棋子占角，相邻的同色棋子通常也变成了稳定子。然后有边缘子集合的概念。由于每步棋都必须至少翻转对手一个棋子，因此对手与空位相邻的棋子越多，你可下的棋就越多，因此你的行动力也就越好。相反地，如果己方棋子很少与空位相邻，那么你的对手就只有很少的棋可下。与空位相邻的棋子就叫作边缘子（frontier disc）。边缘子的集合就叫作边界（frontier）。由以上分析，要尽量增加稳定子，减少边缘子的数量。

根据以上的概念，综合使用参数可以使用加权线性和，用来评估每个位置的价值。

可以使用如下的第一种评价函数：

f1=（a-b）w+S1-S2

以上公式a表示自己的行动力，b表示对方的行动力，w表示权重，S1表示自己的穩定子的数量，S2表示对方的稳定子数量。作为对比，我们采用第二种评价函数：

f2=（a-b）w+C1-C2

其中C1表示自己的棋子数，C2表示对手的棋子数。这两种评价函数经过测试f1函数的胜率表现要明显好于f2。并且f1的水平已经可以达到相当高的水准。

2.4  蒙特卡洛树搜索

蒙特卡洛树搜索（Monte carlo Tree Search，MCTS）是蒙特卡洛算法族的一个，蒙特卡洛算法可以利用随机性来分析极其复杂的情况。蒙特卡洛树搜索算法是通过将蒙特卡洛方法与多叉树搜索进行结合的算法，兼顾了蒙特卡洛方法随机模拟的通用性以及多叉树的广度和深度搜索，能够有效解决决策优化问题[7]。蒙特卡洛搜索树是基于蒙特卡洛方法且通过不断模拟迭代所建立的一颗搜索树，迭代的终止条件通常是预先设定的时间或者条件约束。得到最佳的搜索结果后搜索就会停止，搜索树中的每个终止节点就是达到最佳决策过程中的每个状态[8]。MCTS要评估某个位置价值，采用随机对弈来推演最后得出当前这个位置是否有利。黑白棋的每轮的合法位置就是等价与它的行动力。MCTS算法的每一回合的计算包含如下3个步骤：

（1）将新的棋局添加到MCTS树中。

（2）从这个棋局开始模拟从可选合法位置中随机选一个位置对局。

（3）根据对局结果更新树节点的统计数据。

在一定的时间内重复这个计算过程，最后根据统计数据得到最优结果动作。

在每个回合中可使用的时间是有限的，针对如何在有限的时间内分配有限的预算这一问题，比较好的策略称为搜索树置信区间上界公式（upper confidence bound for trees，UCT）[9]。

该公式定义为：

UCT=w+c

其中w是计算获胜百分率，N表示推演的总数。n表示当前节点开始的所有推演数。参数c表示权衡深入探索和广泛探索时之间的权重。UCT公式为每一个节点提供分数，具有最高UCT分数的节点，可以作为下一次推演的开始点。

3  深度强化学习的应用

深度强化学习（deep reinforcement learning， DRL）是一种结合深度神经网络和强化学习两种方法的融合算法。

深度学习利用深度神经网络的优势，对输入数据具有良好的感知能力，但是决策能力不足。而强化学习感知能力不足但具有良好的决策能力，由此将两者优势结合可以用于解决智能体在复杂高维状态空间中的感知决策问题[10]。

强化学习是心理学和行为学家通过研究发现自然界生物体（包括人类）能够通过不断地试错从而能适应环境的变化。通过最大化累积奖励的方式来学习到最优策略。

强化学习是学习器（又称为代理，agent）学习如何在环境中动作（action），环境中仅有的反馈由奖励信号组成。代理的目标是长期最大化从环境获得的奖励信号。

强化学习问题可以通过马尔科夫决策过程（Markov Decision Processes， MDP）的框架来描述。

3.1  马尔科夫决策过程

MDP是决策理论规划、强化学习及随机过程中一种直观和基本的构造模型。一个马尔科夫决策过程包括状态、动作、转换函数、奖励方程等。

3.1.1  状态

对于建立模型的问题来说，状态是所有信息的唯一特征。例如，在黑白棋中一个完整的棋盘由8行8列的64个方格组成，这是其中一种状态。集合S可以用{s1，…，SN}来定义一个规模为N的有限集合。

3.1.2  动作

动作集合A通過有限集合{a1，…，AK}来定义大小为K的动作空间。默认所有动作都能对应于一个状态，对于s∈S，A（s）=A。

3.1.3  转换函数

通过将动作a∈A运用于状态s∈S，可以得到一个转换集合的概率分布，学习系统就能完成从当前状态s到下一个状态s'的转换，转换函数T的定义为S×A×S→[0，1]。表示含义为当作用于状态s的动作执行后，它的概率为T（s，a，s'）。如果一个动作的结果不依赖以前的动作和状态，而仅仅由当前的状态决定，那么这个系统就具有马尔科夫特性。它可以用以下公式表示：

P（St+1|st，at，st-1，at-1，…）=P（St+1|st，at）=T（st，at，st+1）

马尔科夫动态的核心思想是当前的状态s可以提供所有的信息来为将来做出最优决策。

3.1.4  奖励方程

奖励方程式指在一个状态中完成一个动作后的奖励。状态奖励方程可以定义为R：S→R。奖励方程是马尔科夫决策过程中最重要的部分，因为奖励方程定义了学习的最终目标[11]。在黑白棋游戏中，奖励值可以定义成最终获得比对手多的棋子数量。

价值函数用来估计在某个特定的状态下执行某个动作所能获得的收益值。

在策略π下的状态S的值，表示为V π（S），是预期收益。可以表示为如下公式：

3.2  时间差分学习算法

Q学习是基于离线策略的时间差分算法，时间差分算法是Sutton在1988年提出的，该算法综合了蒙特卡洛算法算和动态规划算法的优点。该算法有两个优点，一是可以无须已知模型动态，第二是无须等到情景结束是才能估计值函数[12]。

状态-行为-奖励-状态-行为（SARSA）是一种在线时间差分控制算法。根据下面的公式来更新值：

这个公式看起来和Q学习公式非常相似，它们都是通过贪婪策略来选择行为，主要的区别在于更新Q值时，Q学习只简单地选取具有最大值的行为，而在SARSA算法中更新Q值时，它也采用贪婪策略来选取行为[13]。

4  模型代码实现与测试

AlphaOthello是一个使用MCTS算法、Q学习算法和SRASA算法的实现人机对弈软件。其中Q学习算法和SRASA算法采用了Keras框架。它是一个基于深度学习的框架。

Keras框架中可以采用函数式API来定义神经网络。函数式API的优势在于可以更加灵活地定义多个输入、输出或者更复杂的连接方式，神经网络函数式API创建模型代码为：

from keras.models import Model

from keras.layers import Dense，Input

model_input=Input（shape=（8，8）

hidden_layer=Dense（32）（ model_input）

output_layer=Dense（24）（hidden_layer）

model=Model（inputs=[model_input]，outputs=[output_layer]

Q学习算法主要代码为：

class QAgent（Agent）：

#训练算法

def train（self，exper，lr=0.1，batch_size=128）：

opt=SGD（lr=lr）

self.model.compile（loss=mse，optimizer=opt）

n=exper.states.shape[0]

num_moves=self.encoder.num_points（）

y=np.zeros（（n，））

actions=np.zeros（（n，num_moves））

for i in range（n）：

action=exper.actions[i]

reward=exper.rewards[i]

actions[i][action]=1

y[i]=reward

self.model.fit（[exper.staes，actions]，y，batch_size=batch_size，epochs=1）

#价值排序，贪婪策略

def rank_moves_eps_greedy（self，values）：

if np.random.random（）

values=np.random.random（values.shape）

ranked_moves=np.argsort（values）

return ranked_moves[：：-1]

...

以上算法代码中，使用随机梯度下降法（stochastic gradient descent， SGD）来更新神经网络的参数，并且使用均值平方差（Mean square differencemse， MSE）做为损失函数。

为了测试算法的性能，将算法生成的下一步策略和WZebra软件进行对弈。

wZebra软件是目前黑白棋AI顶级棋手。在测试中wZebra的对局设置搜索深度采用8步+16步完美，对局时限为30分钟。每种算法对局100局后统计平均表现，wZebra执黑棋，AlphaOthello执白棋。

图4为以wZebra执黑子视角展示对局过程估值图。mcts算法经过调校，总体水平与wZebra低级水平相当，由于实验硬件采用CPU来实现神经网络的计算过程，总体未能战胜wZebra。本实验采用样本数据集为www.skatgame.net GGS 2010数据集，由于数据集数量为15个，数据集数量太少导致学习率不足，导致无法战胜wZebra软件。从曲线圖可以看出Q学习算法白棋在中盘30～40步表现一度接近wZebra。而SARSA算法则在局面的中后盘40～50步表现较好。

5  结  论

本文讨论了从经典搜索算法到基于人工神经网络和深度强化学习三类算法在人机对弈方面的应用。经典搜索算法经过几十年的优化，已经达到了人类一流棋手的水平。而使用人工神经网络和深度强化学习的Q学习算法和SARSA算法要想达到优异地性能表现，依赖于两点：一是高质量的对局样本、二是强大的计算能力。后续要提高深度强化学习类算法的表现，可以从三个方面来优化：

（1）收集更多高质量的对弈样本数据集，用来训练神经网络。

（2）通过对神经网络算法中的超参数调试，来达到更好的效果。

（3）采用GPU来完成神经网络的计算，提高算法能力。

参考文献：

[1] 徐心和，邓志立，王骄，等.机器博弈研究面临的各种挑战 [J].智能系统学报，2008（4）：288-293.

[2] 帕佩拉，费格森.深度学习与围棋 [M].赵普明，译.北京：人民邮电出版社，2021.

[3] LEE K F，MAHAJAN S.The development of a world class Othello program [J].Artificial Intelligence，1990，43（1）：21-36.

[4] ALLIS L V.Searching for Solutions in Games and Artificial Intelligence [D].Maastricht：University of Limburg，1994.

[5] 伊庭齐志著.曹旸，译.AI游戏开发和深度学习进阶[M].北京：机械工业出版社，2021.

[6] LAZARD E.黑白棋战术指南 [M].Paris：FEDERATION FRANCAISE D'OTHELLO，1993.

[7] SCHAEFFER J，HLYNKA M，JUSSILA V. Temporal Difference Learning Applied to a High-Performance Game-Playing Program [J].Theoretical Computer Science，2001，252（1-2）：105-119.

[8] 纪嘉伟.基于蒙特卡洛树搜索的混合激活函数研究 [D].兰州：兰州大学，2021.

[9] WANG Y ，GELLY S .Modifications of UCT and sequence-like simulations for Monte-Carlo Go [C]//IEEE Symposium on Computational Intelligence & Games.Honolulu：IEEE，2007.

[10] 刘全，翟建伟，章宗长，等.深度强化学习综述 [J].计算机学报，2018，41（1）：1-27.

[11] WIERING M，OTTERLO M V.强化学习 [M].赵地，等译.北京：机械工业出版社，2018.

[12] RAVICHANDIRAN S.Python强化学习实战 [M].连晓峰，等译.北京：机械工业出版社，2019.

[13] 唐振韬，邵坤，赵冬斌，等.深度强化学习进展：从AlphaGo到AlphaGo Zero [J].控制理论与应用，2017，34（12）：1529-1546.

作者简介：彭之军（1978—），男，汉族，湖北潜江人，高级工程师，硕士，研究方向：软件工程、人工智能技术、移动互联网技术。