基于神经网络的非线性学术评价指标模拟权重研究


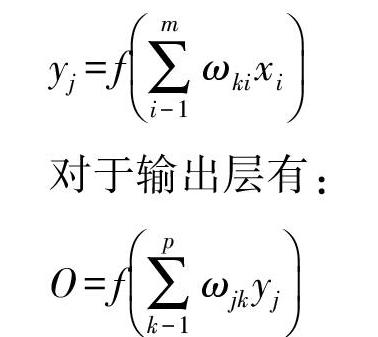
收稿日期:2020-08-01
基金项目:国家社会科学基金项目“学术评价与创新绩效评价问题研究”(项目编号:19FTQB011);浙江省一流学科A类项目(浙江工商大学统计学,管理科学与工程);浙江省自然科学基金重点项目“制造业从数量型创新向质量型创新转型机制研究”(项目编号:Z21G030004)。
作者简介:俞立平(1967-),男,教授,博士,博士生导师,研究方向:技术经济、科技评价。
摘要:[目的/意义]多属性评价方法在学术评价中应用广泛,其中以非线性评价方法为主,这些评价方法降低了权重的作用,使得评价指标与评价结果的关系不直观,也不利于对非线性评价方法进行评估和比较。[方法/过程]本文以因子分析为例,基于JCR2017经济学期刊数据,分别采用多元回归、岭回归、偏最小二乘法、BP神经网络计算模拟权重,以选取最优模拟权重估计方法。[结果/结论]在学术评价中有必要测度非线性评价的模拟权重;BP神经网络是计算模拟权重的最有效手段;模拟权重可以用来进行非线性学术评价方法的评估和选取;模拟权重的应用严重依赖数据。
关键词:学术评价;因子分析;模拟权重;BP神经网络
DOI:10.3969/j.issn.1008-0821.2021.04.013
〔中图分类号〕G302〔文献标识码〕A〔文章编号〕1008-0821(2021)04-0133-13
Research on Simulated Weights of Nonlinear Academic
Evaluation Index Based on Neural Network
Yu Liping
(School of Statistics and Mathematics,Zhejiang Gongshang University,Hangzhou 310018,China)
Abstract:[Purpose/Significance]Multi-attribute evaluation method is widely used in academic evaluation,among which the non-linear evaluation method is the main one.These evaluation methods reduce the role of weight,which makes the relationship between evaluation index and evaluation results not intuitive,and are not conducive to the evaluation and comparison of non-linear evaluation methods.[Method/Process]Taking factor analysis as an example,based on JCR2017 Economic Journal data,multiple regression,ridge regression,partial least square and BP neural network were used to calculate the simulated weights to select the optimal simulated weight estimation method.[Result/Conclusion]It is necessary to measure the simulated weight of nonlinear evaluation in academic evaluation;BP neural network is the most effective method to calculate the simulated weight;Simulated weight can be used to evaluate and select nonlinear academic evaluation methods;The application of simulated weight relies heavily on data.
Key words:academic evaluation;factor analysis;simulated weight;BP neural network
在学术评价中非线性评价方法是一种应用非常广泛的评价方法。从学术评价定量方法的角度,大致可以分为单指标评价与多属性评价两大类,如图1所示。学术评价单指标众多,典型的有h指数、影响因子、特征因子、扩散因子等。由于单指标评价所能提供的信息量有限,因此指标体系多属性评价方法就得到了广泛的应用。目前的泰晤士报大学评价、美国新闻与世界报道周刊的大学评价、北京大学核心期刊评价、CSSCI核心期刊评价等,均采用多属性评价方法。多属性评价方法又分为两大类,一类是加权汇总类评价方法,如层次分析法、熵权法、概率权法、CRITIC等,其特征是评价值与评价指标之间是精确相等的线性关系,该类方法有数种;另一类是非线性评价方法,评价值与评价指标之间是相关关系,常见的主成分分析、因子分析、灰色关联、TOPSIS、数据包络分析等均属于非线性评价方法[1],该类方法有几十种甚至更多。目前在学术评价领域的数千篇多属性评价论文中,采用非线性评价的论文占比超过80%。
指標权重在不同多属性评价方法中作用并不相同。评价指标的权重无疑具有重要意义,从哲学角度,客观权重是遵循自然规律的体现,主观权重是主观能动性的体现;从多属性评价角度,权重是不同指标之间的转换系数;从利益相关者角度,权重是管理者、评价机构、领域专家、公众等利益相关者博弈的均衡结果;从管理角度,权重是管理目标和改进路径的定量体现[2]。在线性评价中,权重的体现是清晰的,明确知道各指标在评价中的意义及权重大小,但在非线性评价中,权重的体现是模糊的,或者说非线性评价将权重问题掩盖了。
在非线性评价方法中权重问题比较复杂。一些非线性评价方法在评价中会用到权重,比如TOPSIS评价、灰色关联评价等尽管是非线性评价方法,但在评价模型的计算过程中可以对各指标赋予权重。也有一些非线性评价方法,在评价中根本不需要权重,如主成分分析、因子分析、数据包络分析等。对于非线性评价,无论是否用到权重,由于评价模型的复杂性,导致人们无法知道各指标的实际重要性。非线性评价缺乏线性评价中评价指标与评价值关系的直观性。
模拟权重的出现是非线性学术评价的重要进步。为了解决无权重非线性评价或有权重非线性评价的指标实际重要性问题,就出现了模拟权重。所谓模拟权重,就是采取一定的统计方法,对非线性评价中各指标的实际发挥作用大小进行计算,得到的结果就是模拟权重[1]。模拟权重的计算意义重大:第一,对于非线性评价方法而言,模拟权重使得评价的主动权又回归到人,而非技术和方法。尽管主观和客观评价优劣一直存在争议,但主观评价可能更重要。查阅辞海,评价的含义是“评估人、事、物的优劣、善恶美丑或合不合理”。从其概念可以看出,评价是一种看法,本来就是主观的。Polonsky M J等[3]指出,在评价学术期刊时,提出只有明确评价的价值取向,才能弄清楚测量期刊的什么属性或特征。得到模拟权重后,评价者就可以进一步分析该非线性评价方法的权重设置是否合理,能否达到评价目的。第二,可以方便对非线性评价方法进行选取。非线性评价方法众多,每种评价方法均有自己的优点和特点,极少有评价方法需要进行方法是否适用的统计检验,所以实际选取往往非常困难。有了模拟权重,既可以根据某种非线性评价方法的优点进行选取,也可以参考模拟权重进行选取。第三,模拟权重使得学术评价更加贴近大众。对于线性学术评价方法,权重是确定的,公众也非常容易理解,而对于非线性评价方法,由于其计算的复杂性,公众往往不太了解,评价结果要得到公众的接受往往比较困难,模拟权重的出现有效地解决了这个问题。
优化模拟权重的计算方法具有重要意义。目前的模拟权重估计,主要采用多元回归、岭回归、偏最小二乘法等方法[1,4],由于学术评价指标之间往往高度相关,以学术期刊评价为例,影响因子、总被引频次、5年影响因子、h指数等指标之间一般相关度非常高,这样就容易产生多重共线性,虽然可以采用岭回归、偏最小二乘法等进行修正,但这种估计是有偏的,会出现拟合优度降低、部分指标的统计检验不通过、部分指标的回归系数为负数等问题,从而降低了模拟权重的估计精度,甚至无法进行模拟权重估计。在这种情况下,借助人工神经网络技术估计模拟权重,就提供了一种新的思路。本文以学术评价中使用频率较多的因子分析为非线性评价方法的代表,基于JCR2017经济学期刊数据,首先采用因子分析进行评价,然后采用多元回归、岭回归、偏最小二乘法、人工神经网络4种方法计算模拟权重,对其进行比较,在此基础上提出模拟权重估计方法选择策略,并得出研究结论。本研究有利于拓展模拟权重的计算方法,解决传统方法计算模拟权重可能出现的问题,推进非线性评价方法的评估与选取,从而推动多属性评价的理论研究,同时也使得评价技术更加为公众所理解,有利于学术评价的公开、公平、公正。
1文献综述
因子分析在科技评价领域应用较广,包括期刊评价、知识产权评价、科技成果转化评价等。因子分析是Spearman C[5]提出的一种重要的客观评价方法,具有能够处理大量多指标数据、便于提取少数公共因子等优点。从因子分析的应用范围看,首先是采用因子分析进行科技评价,赵蓉英等[6]采用因子分析,从多维度、多指标融合的信息计量视角来综合评价学术期刊影响力。王志娟等[7]运用因子分析法对广东省医药卫生期刊影响力水平进行综合评价。冯焕华等[8]采用因子分析法对36种教育学核心期刊的学术水平进行综合评价。李华等[9]选取8个文献计量指标,用因子分析法评价15所大学学报。何莉等[10]选取11个文献计量指标,运用因子分析法对安徽省高校自然科学学报的学术影响力进行综合评价。
因子分析在科技评价中的另外一种应用是结合其他非线性评价方法进行评价,奉国和等[11]用熵权法和因子分析计算各指标权重,然后通过TOPSIS法计算各年期刊综合得分,对图书馆学情报学类期刊进行评价。刘莲花[12]采用TOPSIS法、主成分分析法、因子分析法和加权算术平均法对预防医学与卫生学核心期刊进行了综合评价,然后利用Borda法、平均值法、Copeland法对4种单一评价结果进行循环修正组合评价。张发明等[13]首先利用因子分析法来进行学术期刊评价,然后利用诱导密度算子对评价信息进行集结,再基于最小偏差法确定最终组合评价值并排序。王伟明等[14]首先利用改进的因子分析法对学术期刊进行静态综合评价,然后采用4种非线性评价方法对各年评价结果进行组合评价,再基于最小偏差法得到最终评价结果。
人工神经网络通过一整套简化、抽象的非线性动力学系统来模拟复杂的人脑功能,在科技评价中也开始得到广泛应用。李勤敏等[15]采用主成分分析法提取主成分,用加权秩和比法对作者影响力进行评价,然后用神经算法学习预测,得出预测模型。张瑾[16]将改进BP网络应用到期刊论文的分类领域中,尝试进行期刊论文的自动分类。张和平等[17]运用BP神经网络DEMATEL模型,建立了综合性人文社科期刊的评价模型。张洋等[18]应用人工神经网络评价30个学术网站,并将网站的总得分与其对应PageRank值作相关分析。楼文高等[19]根据科技期刊学术水平评价指标体系和评价标准,采用大样本训练方法建立了学术期刊评价的神经网络模型。刘蕾等[20]采用BP神經网络评价医学类微信公众号学术知识获取效果。李宁[21]采用神经网络研究了其他文献计量指标与影响因子之间的关系。李素英等[22]根据京津冀创业板上市公司数据,采用层次分析法与BP神经网络相结合,对科技型中小企业创新能力进行评价。周宏[23]采用BP神经网络方法对高校科技成果转化进行综合评价。曾莉等[24]建立BP神经网络模型,对科技型中小企业知识产权质押融资风险进行评价。刘长平[25]将数据包络分析与BP神经网络相结合,构建了企业科技成果转化综合评价DEA-BP模型。
关于模拟权重的研究,赵宇等[26]设计一种基于权重和方法组合的评价导向随机模拟算法,结合主成分分析和TOPSIS两种评价方法,将二者的评估结果通过设置权重进行加权综合,使其接近专家评审结果。翟珊珊等[27]研究了组合预测中组合权重的确定问题,分析了组合预测中几种常用组合权重确定方法对提高预测精度的效果,并进行仿真研究。俞立平[4]提出采用岭回归或偏最小二乘法在計算学术评价中的模拟权重。
从现有的研究看,关于因子分析在学术评价中的应用研究成果比较丰富,既作为主要方法用于评价,也作为评价方法之一结合其他评价方法进行综合评价。关于非线性评价中的权重组合问题,更多作为组合评价方法或对某种评价优化方法进行权重的拟合或仿真,只有少量研究关注非线性评价中的模拟权重问题。神经网络在学术评价中的应用已经开始,目前主要集中在评价与分类,还没有涉及模拟权重。总体上,在以下方面有待进一步深入。
第一,学术评价中非线性科技评价方法众多,因子分析方法仅仅是其中一个代表。权重在非线性科技评价中的地位被严重弱化,模拟权重的问题没有得到足够的关注,迫切需要加强该方面的研究。
第二,从现有模拟权重的计算方法来看,主要采用多元回归、岭回归、偏最小二乘法等进行估计,存在着估计精度不高、部分学术评价指标回归系数可能出现负数、难以通过t检验等问题,其估计方法有待进一步拓展。
第三,人工神经网络用于学术评价,其基本原理就是通过权重模拟实现的,当然这些是隐含的。现有研究主要关注采用人工神经网络进行评价,而较少从模拟权重的角度来比较不同评价指标的重要性。
第四,如果模拟权重的估计方法有多种,如何选择最佳模拟权重估计方法,其选择标准是什么?
2研究方法
2.1研究框架
本文针对学术评价中非线性评价指标模拟权重问题,首先要解决的是模拟权重的测度方法,选取出最佳测度方法,在得到模拟权重后进行深度分析。分析视角包括两个方面:第一是模拟权重测度方法的选择依据;第二是模拟权重得到后对非线性评价方法的选取以及学术评价产生的深度影响,其研究框架如图2所示。
因子分析在非线性评价方法具有较好的代表性。非线性评价方法众多,诸如模糊综合评判法、主成分方法、因子分析法、灰色关联评价、集对分析、数据包络分析方法、递阶综合评价方法、人工神经网络、康拓对角线法、证据理论、秩和比、突变论、支持向量机、TOPSIS、VIKOR、BORDA、TOPSIS、ELECTRE等。随着管理科学与多元统计的发展,还会不断涌现出新的评价方法。在学术评价中,因子分析应用本来就较多,此外由于因子分析与主成分分析原理相近,选取因子分析作为非线性评价方法拥有更好的代表性。
在采用因子分析评价后,就可以进行模拟权重的计算了。关于模拟权重的计算方法,可行的包括多元回归、岭回归、偏最小二乘法等,这是传统的基于回归分析的方法。而人工神经网络是一种新的思路,实现的技术路径与回归完全不同,是一种崭新的尝试。
根据模拟权重的计算过程与计算结果,可以从3个视角分析:第一是模拟权重的计算方法比较,确定在各种情况下的筛选策略;第二是模拟权重估计结果的分析,可以深度分析因子分析方法的评价偏好、评价侧重点;第三是在此基础上可以对因子分析是否适用于学术评价进行评估。最后根据以上内容得出研究结论。
2.2传统模拟权重估计方法简介
1)传统回归
当学术评价指标较少、指标间相关度不高时,采用多元回归就可以进行模拟权重估计,其公式如下:
log(Y)=c0+c1log(X1)+c2log(X2)+…+cnlog(Xn)(1)
式(1)中,Y表示非线性评价值,Xi为评价指标(0 将回归系数ci进行归一化处理,就得到了各评价指标的模拟权重ωi: ωi=ci∑ni=1ci(2) 在计算模拟权重时,式(2)成立的前提条件是所有回归系数必须大于0,因为权重不能为负数,但是没有哪种回归方法可以提供这种保证。此外,如果回归系数没有通过统计检验,从理论上说,该评价指标与评价结果无关,这也是一个问题。 另外一个问题是,当学术评价指标众多,指标之间容易存在高度多重共线性,传统的删除部分指标、增加样本量等降低多重共线性的方法又不能采用,在这种情况下,采用岭回归可以大幅降低多重共线性问题。 2)岭回归 岭回归由Horel A E等[28]提出,本质上是一种经过优化的最小二乘法,是一种专门用于共线性数据分析的有偏估计回归方法。经典的回归是计算: =(X′X)-1X′y(3) 当变量存在多重共线性时,矩阵X′X几乎是奇异的,会导致估计结果的方差非常高。解决方法是通过变换矩阵的特征值来回避这个问题: =(X′X+kI)-1X′y(4) 式(4)可以减少估计方差,但这种估计是有偏的。如果减少的方差远远高于增加的估计偏差,均方误差减少了,那么岭回归就是有效的。岭回归就是用X′X+kI代替正规方程中的X′X,通过选择合适的k,使方差较小估计的偏差也较小,一般通过作图来选择恰当的参数k。 从以上岭回归的原理可以看出,虽然大大降低了多重共线性问题,但是回归系数可能也会出现负数,也有可能无法通过统计检验,并且岭回归也是有偏的,那么回归系数就不是最佳的,由此也会带来模拟权重精度下降。 3)偏最小二乘法 偏最小二乘法(Partial Least Squares,PLS)由Wold S等[29]提出,它结合了多元回归、主成分分析、典型相关分析的优点,尤其适用于变量存在多重共线性以及变量个数较多而样本较少时的情况。
对于自变量X和因变量Y,首先基于主成分分析,从X中提取成分t1,从Y中提取成分u1,同时使得t1和u1的变异方差达到最大,即:
Var(t1)→max Var(u1)→max(5)
根据回归建模的要求,同时考虑到t1对u1有最大解释能力,基于典型相关分析,要求t1和u1的相关系数最大,即:
r(t1,u1)→max(6)
同時考虑以上两方面因素,以t1和u1协方差最大作为提取条件:
Cov(t1,u1)=Var(t1)·Var(u1)·r(t1,u1)→max(7)
t1和u1提取后,分别进行X对t1和Y对t1进行回归,如果回归方程满足PRESS精度,则算法终止,否则分别从残余数据中继续提取t2和u2,直到满足PRESS精度要求。由于t和u是彼此正交的,因而大大克服了多重共线性问题。
如果最终从X中提取了m个成分t1、t2…tm,从Y中提取了q个成分u1、u2…um,则进行Yk对于t1、t2…tm的回归,最后再将其转换为Yk对于x1、x2…xm的方程。
2.3人工神经网络模型
人工神经网络是一整套简化、抽象、模拟人脑功能的极其复杂的非线性动力学系统。BP神经网络模型是对人脑神经网络若干基本特性的抽象和模拟,可以进行分布式并行信息处理[30]。典型的人工神经网络由1个输入层,若干个隐蔽层和1个输出层构成,如图3所示,神经网络的大部分由隐蔽层构成。每层单元节点数量均可以是多个,每层单元节点与它两边层的各个单元节点都是连通的。每个连接都赋予1个权重值,表明前一个单元的输出对下一个单元输出的影响力。
神经网络需要经过训练和学习才能生成期望的输出,其学习步骤如下:
1)设置初始参数,ω为初始权重,θ为临界值,取随机较小正数。
2)将样本数据加载到神经网络,计算隐蔽层和输出层的输出,对于隐蔽层有:
yj=f∑mi-1ωkixi(8)
对于输出层有:
O=f∑pk-1ωjkyj(9)
式(8)中,f(x)为单极Sigmoid函数。式(9)中,f(x)为纯线性函数;I、j、k分别为神经网络的输入、输出、隐蔽单元的代号;m为输入单元数、p为隐蔽单元数;ωki为输入神经元i到隐含神经元k的链接权重,ωjk为输出神经元j到隐含神经元k的链接权重。
3)各层权重的调整量为:
Vω=ηδjyj(10)
式(10)中,η为学习率,也称为比例系数,一般取(0,1)区间中一个较小的数;δj是一个与输出偏差相关的数值,即dj-yj,dj表示期望输出数据。
对于输出节点有:
δj=ηj(1-yj)(dj-yj)(11)
对于隐蔽节点有:
δj=xi(1-xi)∑pk=1δkωki(12)
式(12)中,k指要把输出层节点取遍,误差δj是从输出层反向逐层计算的。
4)各层神经元调整后的权重为:
ωki(t)=ωki(t-1)+Vωki(13)
式(13)中,t为学习次数,其计算是个循环迭代过程,每轮计算均将各神经元之间的权重调整一遍,直到输出误差小于某一允许范围为止。
2.4期刊评价人工神经网络模型
本文基于JCR2017经济学期刊进行研究,JCR公布的指标包括总被引频次、影响因子、他引影响因子、5年影响因子、即年指标、载文量、被引半衰期、引用半衰期、特征因子、论文影响分值、文献选出率、影响因子百分位、标准特征因子。这些指标中,载文量和文献选出率不能说明期刊的影响力与学术质量,不宜选取;影响因子百分位本质上是排序,属于非参数数据,当然也不宜选取;标准特征因子是根据特征因子计算而来,信息有重复之处,也不宜选取。在删除掉这些指标后,实际采用余下的9个指标,首先采用因子分析进行评价,然后再采用人工神经网络进行学习,得到各指标的模拟权重,并进行后续分析。本文的学术期刊人工神经网络结构如图4所示。
根据Komogorov定理,对于任意连续函数,可以用三层网络来精确实现,即只要用1个隐蔽层就可以。采用因子分析评价学术期刊,评价指标与评价结果之间的关系总体不算复杂,并且评价结果值是连续的,因此选用3层网络即包含1个隐蔽层的模型来进行学习就足够。
关于隐蔽层节点数量的确定,当隐蔽层数量太少时,学习过程不容易收敛;但当隐蔽层节点数太多时,网络映射能力增强,容易收敛,但容易出现过度学习现象,即将异常点(随机噪声)也纳入学习结果,从而导致容错率降低。隐含节点的选取方法有构造法、删除法、黄金分割法等,本文采用删除法进行逐步试算,以确定最佳隐蔽层数量。
3研究数据与实证结果
3.1研究数据
考虑到人工神经网络学习需要的样本数量不能太小,因此本文选取JCR2017中期刊数量相对较多的经济学期刊为例进行研究。JCR2017共有期刊353种,在这些期刊中,5年影响因子有缺失的期刊13种,即年指标有缺失的期刊1种,被引半衰期有缺失的期刊18种,引用半衰期有缺失的1种,论文影响分值有缺失的13种,当然有些期刊的缺失指标有多个。经过数据清洗,删除了32种期刊,余下321种期刊。评价指标的数据描述统计如表1所示。
此外被引半衰期和引用半衰期属于反向指标,在评价以及做后续分析时必须进行正向处理,本文采用用极大值减去各指标值的方法先转化为正向指标,然后再采用传统标准化方法进行评价。
3.2因子分析评价
采用因子分析法对经济学期刊进行评价,首先要进行KMO检验与Bartlett检验,以决定是否能采用因子分析。KMO检验值为0.778,Bartlett检验值为3 312.777,p值为0.000,满足进行因子分析的前提条件,可以采用因子分析进行评价。
因子旋转矩阵如表2所示,采用最大方差法进行旋转,得到两个公共因子,根据系数大小进行分类:第一公共因子由总被引频次、影响因子、他引影响因子、5年影响因子、即年指标、特征因子、论文影响分值7个指标组成,可以将其命名为期刊影响力因子;第二公共因子由被引半衰期、引用半衰期两个指标组成,可以将其命名为期刊时效因子。
第一公共因子的方差贡献率为58.790%,第二公共因子的方差贡献率为14.503%,两者一共解释了原始数据的73.293%,总体上是有效的。根据方差贡献率加权,得到因子分析的评价结果。
需要说明的是,由于后续分析需要对因子分析的评价值取对数进行回归,而因子分析的评价值有负数,不能取对数,需要进行进一步处理。通过对因子分析评价值的分析,发现极小值为-0.931,因此对因子分析的评价值全部加上1,这样就使得所有评价结果均为正值。
3.3基于回归分析计算学术评价指标模拟权重
首先采用多元回归对因子分析的评价结果与评价指标进行回归,结果如表3所示。模型的拟合优度较高,R2为0.949。9个评价指标中他引影响因子、被引半衰期没有通过统计检验,其他指标均在1%的水平下通过了统计检验。回归系数较大的指标主要是引用半衰期(1.151)、影响因子(0.227)。由于被引半衰期和特征因子的回归系数为负数,所以无法进一步根据回归系数大小比例来计算模拟权重。
其次采用岭回归对因子分析的评价值与评价指标进行回归,其岭迹图如图5所示,当k=0.2时,模型相对稳定,回归结果同样如表3所示。模型的拟合优度中等偏高,R2为0.823。回归系数较大的指标是论文影响分值、总被引频次、即年指标、5年影响因子,这个结果比多元回归有所改进。但是由于影响因子、被引半衰期、引用半衰期、特征因子的回归系数为负数,所以同样不能进一步计算模拟权重。
最后采用偏最小二乘法估计因子分析结果与评价指标之间的关系,方差解释比例如表4所示,随着隐含成分的增加,其拟合优度R2也在提高,因此选取隐含成分为5时的回归结果,其拟合优度为0.893,属于偏高水平,回归结果同样如表3所示。
从偏最小二乘法的回归结果看,即年指标(1.290)、论文影响分值(1.198)、影响因子(1.176)、他引影响因子(1.146)等指标的权重较大,而特征因子(0.367)、被引半衰期(0.650)、引用半衰期(0.676)的权重较小。所有的回归系数均为正数,因此可以进一步计算模拟权重,其结果如表5所示。
3.4人工神经网络模拟权重估计
通过试算,确定隐蔽层为1层,4个隐含指标,基于BP神经网络进行学习,迭代次数选择1 000次,拟合曲线如图6所示。最终BP神经网络学习模型中,评价值与评价指标的相关系数为0.994,拟合优度R2为0.988,具有极好的拟合效果。
BP神经网络得到模拟权重如表6所示。引用半衰期的权重拥有绝对支配地位,为0.772,影响因子、5年影响因子、他引影响因子的权重在同一数量级,分别为0.074、0.059、0.045,其他指标的权重则不高。为了进行比较,将BP神经网络的权重与偏最小二乘法计算的权重同时呈现在表6中。
从表6可以看出,由于模拟权重估计的方法完全不同,模拟权重的结果也相差较大。偏最小二乘法模拟权重结果中,被引半衰期的权重仅为0.077,完全可以忽略不计。而BP神经网络模拟结果中,被引半衰期的权重却高达0.772,完全处于主宰地位。由于这两种模拟权重结果相差较大,因此只能选取其中的一种来进行深度分析。
3.5几个问题的讨论
1)模拟权重估计方法的选择问题
几种模拟权重方法的比较如表7所示。从方法应用的前提条件看,分析视角可以从样本大小、数据分布与多重共线性处理、指标相关度4个方面进行。
從样本大小看,多元回归和岭回归适用于中等样本,必须达到回归的基本要求,而偏最小二乘法可以适用于小样本,BP神经网络由于要进行机器学习,所以必须是中等以上样本。
从评价指标的数据分布看,多元回归与岭回归必须服从正态分布,而偏最小二乘法与BP神经网络没有数据分布要求。本文JCR2017经济学期刊的所有评价指标以及评价结果均不服从正态分布,从这个角度,无法采用多元回归和岭回归来计算模拟权重。文献计量指标往往呈现偏态分布或幂律分布,并不服从正态分布[31-32]。
从多重共线性的处理看,多元回归对多重共线性的处理办法较差,因为不能删除任何评价指标,也不能方便地增加样本数量。岭回归对多重共线性的处理方法较好,极大地进行了改进,而偏最小二乘法则较好解决了多重共线性问题。BP神经网络则根本不考虑多重共线性问题,是终极解决方案。
指标相关这个要求比较有趣,在回归中,最不希望出现的就是指标间相关,容易产生多重共线性,对于多元回归、岭回归均是如此,而偏最小二乘法涉及主成分分析,其前提条件指标间必须相关,也就是说,如果指标间相关度不高时,是不适合采用偏最小二乘法估计模拟权重的。BP神经网络对此没有要求,自由度较大。
从模拟权重的计算过程看,分析视角又可以从回归系数(权重)的符号、回归系数(权重)检验、回归系数(权重)准确度这3个方面展开。
在模拟权重估计中,基于回归分析的估计方法必须保证回归系数为正数,但多元回归、岭回归均不能提供这种保证,偏最小二乘法虽然也不能提供这种保证,但在大概率的情况下,可以保证回归系数为正。而人工神经网络模拟权重则永远为正,根本不需要考虑正负问题。
基于回归分析的模拟权重估计同样要兼顾回归系数的统计检验问题,因为如果评价指标的回归系数没有通过统计检验,说明该指标与评价值无关。多元回归、岭回归、偏最小二乘法均有评价指标回归系数的统计检验问题,而人工神经网络没有。当然,对回归系数的统计检验这个要求可以适当放宽,但不能没有,从这个角度,人工神经网络最优,没有任何问题。
最后是权重模拟精度问题,多元回归采用最小二乘法进行估计,其精度是最好的。而岭回归和偏最小二乘法均是有偏估计,也就是说回归系数是有误差的。BP神经网络是通过机器学习来拟合权重,每次学习结果均不一样,所以其精度也会有所损失。一种改进方法是通过多次学习,取每次学习结果权重的平均值作为模拟权重结果。
从整个模型的拟合结果角度,可以通过拟合优度来加以判断,在同等情况下,多元回归、岭回归、偏最小二乘法的拟合优度一般,而人工神经网络的拟合优度往往很高,而且可以通过改进学习参数加以控制。本文偏最小二乘法的拟合优度为0.869,而人工神经网络拟合优度高达0.988,所以采用人工神经网络计算模拟权重最佳。
基于以上分析,非线性评价方法模拟权重估计方法的选择策略如下:
第一,一般情况下,没有必要选择多元回归和岭回归。
第二,样本很小情况下,无法计算模拟权重。
第三,小样本情况下,当指标相关度较高时,可以采用偏最小二乘法计算模拟权重,一旦发现回归系数出现负数,则采用BP神经网络。当然,在这种情况下,模型的估计精度会受到影响。
第四,中等及以上样本情况下,首选人工神经网络计算模拟权重,可以通过多次机器学习取平均值的方法来提高模拟权重的精度。
第五,中等及以上样本情况下,如果指标间相关度高,偏最小二乘法拟合优度很高,回归系数也全部为正数,可以考虑采用偏最小二乘法模拟权重与BP神经网络模拟权重的均值作为模拟权重的结果。
2)模拟权重结果的分析
基于以上分析选择策略,本文由于采用大样本,偏最小二乘法的回归系数均为正数,但由于其拟合优度远低于BP神经网络,KMO值不高,即指标间相关度中等,所以最终采取BP神经网络来计算模拟权重。
本文至此通过几种模拟权重估计方法的比较,最终根据BP神经网络得出了评价指标的模拟权重。或者说,模拟权重提供了反映因子分析评价特点的另外一个视角,并且更加直观,其最大特点是引用半衰期的权重极高。
下面的分析思路从两个角度展开:第一,如果这种结果可以进一步进行验证,并且可以得到合理的解释,那么说明采用因子分析是合适的,可以对因子分析的评价特点进行进一步的分析;第二,如果结果难以得到进一步的验证,无论能否找到合理的解释,那么可能就是非线性评价方法存在问题,说明不适合采用因子分析来评价经济学期刊。
评价指标及评价结果的相关系数如表8所示。引用半衰期与评价值的相关系数偏低,引用半衰期与因子分析评价值的相关系数为0.483,低于5年影响因子(0.905)、影响因子(0.884)、他引影响因子(0.873)、论文影响分值(0.773)、总被引频次(0.738)、特征因子(0.629)。并且这些相关系数均通过了统计检验,说明从统计意义上,这些评价指标与评价值是相关的。
当然还有另外一个原因会导致引用半衰期与因子分析评价值相关度偏低,那就是它们之间可能存在非线性相关,继续引入引用半衰期的2次项、3次项进行回归,结果如下:
log(y)=-28.614+24.300log(CHL2)-7.337log2(CHL2)+0.746log3(CHL3)(14)
(0.815)(-0.867)(0.967)R2=0.291 n=321
回归结果表明,引用半衰期与因子分析评价值之间并不存在非线性关系,所有回归系数均没有通过统计检验,拟合优度R2很低,只有0.291。所以可以得出结论,采用因子分析来评价2016年JCR经济学期刊是不合适的。这个结论是通过BP神经网络计算模拟权重得出的,如果不计算模拟权重,根本无法对因子分析评价方法是否适用于学术评价进行深度讨论,本文提供了一个新的视角,拓展了前人的研究。
4研究结论
4.1在学术评价中有必要测度非线性评价方法的模拟权重
在學术评价中,多属性评价方法得到了广泛的应用,其中以大量的非线性评价方法为主,因子分析仅仅是其中一个重要的代表。非线性评价方法种类繁多,原理不一,但其共性是降低甚至消除了多属性评价中指标权重的地位和作用。评价指标的权重问题是多属性评价的基础问题,忽视这个问题必然对学术评价带来不良影响。模拟权重是评估非线性学术评价指标重要性的重要手段,必将对非线性评价在学术评价中的应用产生深远的影响。
4.2BP神经网络是估计学术评价指标模拟权重的最有效手段
本文在对多元回归、岭回归、偏最小二乘法、人工神经网络4种模拟权重估计方法原理分析的基础上,从样本大小、数据分布、多重共线性处理、指标相关度、回归系数符号、回归系数统计检验、回归系数估计精度、拟合优度等方面对4种方法进行了比较,以因子分析作为非线性评价方法的代表,采用JCR经济学期刊进行了实证研究,结果表明,BP神经网络是这4种方法中最合适的模拟权重估计方法。
4.3模拟权重可以用来进行非线性学术评价方法的评估和选取非线性评价方法原理众多,评价指标与评价值的关系复杂,不同非线性评价方法之间的比较十分困难。一旦计算出模拟权重,就可以和线性评价方法一样,对各指标的重要性进行分析评估,一方面可以分析某种非线性评价方法的特点,评估各指标的重要性;另一方面可以用来对非线性评价方法进行选取。如果模拟权重配置和管理需要与专家意见基本相当,说明采用该非线性评价方法较好,如果偏差较大,则说明这个非线性评价方法根本不适用于该评价。在面临多种非线性评价方法可以选取的情况下,模拟权重提供了一种非常有效的比较手段。对于任何学科的期刊评价,如果采用非线性评价方法,都有必要采用本文的方法进行进一步的筛选和比较。
4.4模拟权重的应用严重依赖数据
本文采用因子分析作为非线性评价方法之一,基于JCR2017经济学期刊进行实证研究,通过模拟权重的计算和分析,发现因子分析并不适用于评价经济学期刊。需要注意的是,并不是说因子分析不能用来评价其他学术期刊,甚至也不能说因子分析不能用于评价2016年经济学期刊,只能说不能采用因子分析评价2017年JCR经济学期刊。因为模拟权重的计算是严重依赖数据的,从方法论的角度具有通用性,从应用的角度具有特殊性,应该结合具体数据来进行分析。
本文首次将BP人工神经网络用于非线性评价的模拟权重估计,提供了一种新的分析非线性评价方法的手段。本文提出的研究方法不仅可以应用在学术评价中,也广泛适用于其他领域的评价。期待有更多的非线性评价模拟权重估计方法出现,共同推进多属性评价的进展。
参考文献
[1]俞立平,宋夏云.期刊评价中非线性评价方法选取的检验研究[J].中国科技期刊研究,2014,25(8):1063-1067.
[2]俞立平,宋夏云,邹文璨,等.科技评价权重的本质研究[J].情报杂志,2018,37(2):117-121.
[3]Polonsky M J,Whitelaw P.What Are We Measuring When We Evaluate Journals?[J].Journal of Marketing Education,2005,27(2):189- 201.
[4]俞立平.科技评价中关键指标的测度方法研究——以学术期刊评价为例[J].图书情报工作,2017,61(18):93-97.
[5]Spearman C.The Proof and Measurement of Association Between Two Things.By C.Spearman,1904[J].American Journal of Psychology,1987,100(3/4):441-471.
[6]赵蓉英,王旭.多维信息计量视角下学术期刊影响力评价研究——以国际LIS期刊为例[J].中国科技期刊研究,2019,30(7):773-781.
[7]王志娟,姚亚楠,杨克魁.基于因子分析法的科技期刊学术影响力综合评价及发展建议——以广东省医药卫生期刊为统计源[J].中国科技期刊研究,2018,29(10):1036-1041.
[8]冯焕华,任博.基于因子分析的教育学期刊学术水平综合评价研究[J].软件导刊(教育技术),2017,16(9):4-6.
[9]李华,李政.基于因子分析法評价期刊的学术影响力[J].南通职业大学学报,2010,24(2):72-75.
[10]何莉,董梅生,丁吉海,等.安徽省高校自然科学学报学术影响力综合评价分析——基于因子分析法[J].中国科技期刊研究,2014,25(3):427-431.
[11]奉国和,周榕鑫,武佳佳.基于熵权TOPSIS及因子分析的学术期刊综合评价研究[J].图书情报工作,2018,62(17):84-95.
[12]刘莲花.基于循环修正思路的科技期刊综合评价[J].中国科技期刊研究,2016,27(6):645-649.
[13]张发明,王伟明.基于因子分析和诱导密度算子的学术期刊组合评价[J].情报杂志,2018,37(3):165-166,170,167-169.
[14]王伟明,徐海燕.基于最小偏差法的学术期刊动态组合评价[J].情报杂志,2019,38(5):102-108.
[15]李勤敏,郭进利.基于主成分分析和神经网络对作者影响力的评估[J].情报学报,2019,38(7):709-715.
[16]张瑾.基于改进BP网络的中文期刊论文分类方法[J].河南图书馆学刊,2014,34(5):61-63.
[17]张和平,陈齐海.期刊学术影响力测度指标结构关系研究——基于BP神经网络DEMATEL模型的实证[J].现代情报,2018,38(1):87-91,99.
[18]张洋,梁丽,黄亚明.学术网络资源评价指标体系的构建——应用人工神经网络制定学术网站评价指标体系[J].中国科技信息,2009,(12):316-318.
[19]楼文高,张卫,杨雪梅.科技期刊学术水平综合评价的神经网络模型[J].情报杂志,2009,28(9):73-77.
[20]刘蕾,于国泳,林鑫,等.基于BP神经网络的医学类微信公众号学术知识获取效果评价模型构建[J].中华医学图书情报杂志,2019,28(2):35-44.
[21]李宁.基于BP神经网络的管理类期刊影响因子的影响因素分析[J].陕西教育学院学报,2007,(3):83-86.
[22]李素英,王贝贝,冯雯.基于AHP-BP的科技型中小企业创新能力评价研究——以京津冀创业板上市公司数据为样本[J].会计之友,2017,(24):60-64.
[23]周宏.基于BP神经网络的高校科技成果转化的综合评价[J].统计与决策,2009,(17):79-81.
[24]曾莉,王明.基于BP神经网络的科技型中小企业知识产权质押融资风险评价[J].科技管理研究,2016,36(23):164-167.
[25]刘长平.基于DEA和BP神经网络的企业科技成果转化综合评价及实证分析[J].科技和产业,2015,15(8):98-101.
[26]赵宇,王晶华,黄思明,等.基于后评估的科技成果评价导向模拟分析研究[J].中国管理科学,2014,22(S1):90-94.
[27]翟珊珊,段婕.组合权重确定方法的仿真对比分析[J].统计与决策,2015,(24):83-85.
[28]Hoerl A E,Kennard R W.Ridge Regression:Biased Estimation for Nonorthogonal Problems[J].Technometrics,1970,(12):55-67.
[29]Wold S,Martens H,Wold H.The Multivariate Calibration Problem in Chemistry Solved By the PLS Method[J].Springer-Verlag,Heidelberg,1983:286-293.
[30]Rumelhart D E,Hinton G E,Williams R J.Learning Representations By Back-propagation Error[J].Nature,1998,323(9):533-536.
[31]Vinkler P.Introducing the Current Contribution Index for Characterizing the Recent,Relevant Impact of Journals,Scientometrics,2008,79(2):409-420.
[32]Seglen P O.The Skewness of Science[J].Journal of the American Society for Information Science,1992,43(9):628-638.
(责任编辑:孙国雷)

