雷达被截获距离的等效试验方法研究*

曾小东

(中国电子科技集团公司第十研究所，四川 成都610036)

0 引言

雷达被ESM 侦察设备截获距离试验是考核鉴定雷达低截获性能的重要试验内容之一[1-3]。 在现代战场电磁对抗条件下，雷达所面临的电磁环境异常复杂，侦收雷达信号的ESM 侦察设备十分繁多。 要考核雷达被各种ESM 侦察设备截获距离，无论从效率还是从耗费都不可能用“穷尽法”来选用各种ESM 侦察设备来做实装对抗试验。 与此同时，往往要选用所期望的ESM 侦察设备来进行被截获距离试验是极其困难的，甚至是不可能的。

雷达可以采用功率控制、复杂调制波形[4-5]、灵活的扫描样式和超低副瓣等低截获概率设计[6-7]，所以ESM侦察设备可能侦收不同功率控制量的雷达信号，也可能侦收不同副瓣的雷达信号。因此想要考核雷达在不同工作状态下的被截获距离，亦是不现实的。

本文研究的等效试验方法是在选定同样的试验条件下的等效折算[8-10]，如假定两次试验，雷达的发射功率相同，对一次试验的被截获距离试验结果折算到其他条件下的等效被截获距离。等效试验方法可以解决解决空中试飞中，由于配试设备的条件限制，如ESM 侦察设备的系统灵敏度等限制，条件与研制要求的规定不一致，将现有配试条件下得到的雷达被截获距离等效折算到研制要求配试条件下的雷达被截获距离。

1 等效模型

雷达的低截获技术不断演化，通常ESM 侦察设备得到高的信号强度，使得截获接收机可以采用门限检测来获取每部雷达的脉冲，然后估计其参数[11]。 雷达被截获距离是表征雷达低截获概率技术是否有效的关键参数。在雷达鉴定时，需要通过试验验证其被截获距离是否满足设计指标，试飞是最直接的手段，然而考虑到运行成本以及试验的完备性，通常首先需要以地面试验进行等效测试。 本文建立了雷达被期望ESM 侦察设备截获距离和替代ESM 侦察设备截获距离的等效模型，可以支撑等效测试中的雷达被截获距离折算。

雷达被期望ESM 侦察设备截获距离为：

同理可得，雷达被替代ESM 侦察设备截获距离为：

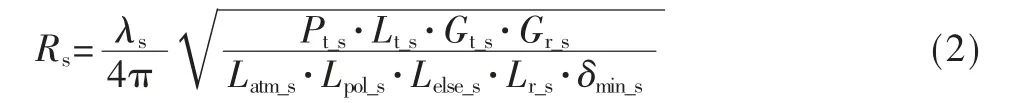
式中，λi和λs分别为期望试验和替代试验中的雷达信号波长，Pt_i和Pt_s分别为期望试验和替代试验中的雷达信号发射功率，Lt_i和Lt_s分别为期望试验和替代试验中的雷达发射损耗，Gt_i和Gt_s分别为期望试验和替代试验中的雷达发射天线增益，Gr_i和Gr_s分别为期望试验和替代试验中的ESM 侦察设备接收天线增益，Latm_i和Latm_s分别为期望试验和替代试验中的大气衰减，Lpol_i和Lpol_s分别为期望试验和替代试验中的极化损耗，Lelse_i和Lelse_s分别为期望试验和替代试验中的其他损耗，Lr_i和Lr_s分别为期望试验和替代试验中ESM 侦察设备的接收损耗，δmin_i和δmin_s分别为期望试验和替代试验中ESM 侦察设备的接收机灵敏度。

两式相除，得到等效模型为：

在试验过程中，使用同一部被试雷达，使得期望试验中的雷达参数和替代试验中的保持一致， 即发射损耗，工作波长等参数一致，Lt_i=Lt_si，λi=λs。

同时， 假定极化损耗和其他损耗也近似相等，Lpol_i=Lpol_s，Lelse_i=Lelse_s。 于是，式(3)简化为：

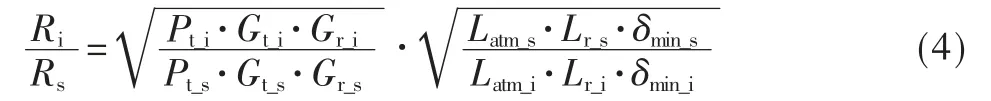
在理想情况下，不考虑大气衰减，式(4)进一步简化为：

因为ESM 侦察设备的系统灵敏度Smin和接收机灵敏度δ 有如下转换关系：

式(6)可改写为：

式中，Smin_i和Smin_s分别为期望试验和替代试验中ESM 侦察设备的系统灵敏度。

对于式(7)，在试验过程中，一方面需要判断期望ESM侦察设备和替代ESM 侦察设备截获时，雷达是否进行功率控制；另一方面需要区分期望ESM 侦察设备和替代ESM 侦察设备分别截获的是雷达主瓣、副瓣以及第几副瓣。因此，在试验过程中，需要实时记录雷达的功率控制量，以计算等效模型中的Pt_i和Pt_s。 同时，还需要实时记录雷达的扫描角度、天线方向图、雷达平台经纬高、雷达平台姿态角以及ESM 侦察设备平台的经纬高，以计算等效模型中的Gt_i和Gt_s。 Gt_i和Gt_s统称为ESM 侦察设备平台方向的雷达发射增益Gt，其计算步骤如下：

(1)获取雷达的扫描角度；

(2)根据雷达的扫描角度，查询该雷达的扫描角度对应的天线方向图；

(3)根据雷达平台经纬高、雷达平台姿态角以及ESM侦察设备平台的经纬高，计算ESM 侦察设备平台相对于雷达平台的方位角和俯仰角[12]。

首先计算ESM 侦察设备平台相对雷达平台的位置矢量在大地直角坐标系下的表示[x，y，z]。

其中：

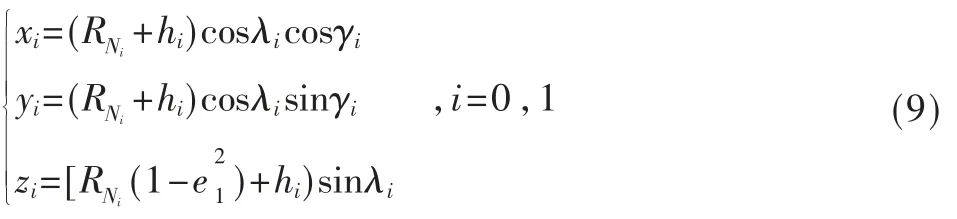
式中，(x0，y0，z0)和(x1，y1，z1)分别为雷达平台和ESM 侦察设 备 平 台 的 大 地 直 角 位 置 坐 标。 (γ0，λ0，h0)和(γ1，λ1，h1)分别为雷达平台和ESM 侦察设备平台的经度、纬度和高度，e1表示地球第一偏心率，RNi表示卯酉圈地球曲率半径[13-14]。

式中，c()表示cos()，s()表示sin()，(Ψ，θ，φ)为雷达平台的偏航角、俯仰角和横滚角。

依据[xb，yb，zb]，计算得到ESM 侦察设备平台相对雷达平台的方位角β 和俯仰角ε。

(4)根据期望试验和替代试验中的天线方向图、方位角和俯仰角，得到Gt_i和Gt_s。

根据不同的试验场景，式(7)有不同的应用，可以解决相应的等效折算问题[15]。

试验场景1：期望ESM 侦察设备和替代ESM 侦察设备为同一设备，雷达不进行功率控制，主瓣被截获距离和副瓣被截获距离折算。

式中，Rm为主瓣被截获距离，Rl为副瓣被截获距离。

试验场景2：期望ESM 侦察设备和替代ESM 侦察设备为同一设备，雷达进行功率控制，不同功率控制量下的主瓣被截获距离折算。

式中，Rnc为满功率时主瓣被截获距离，Rc为功率控制时主瓣被截获距离。

试验场景3：期望ESM 侦察设备和替代ESM 侦察设备为不同设备，雷达发射功率和发射增益相同，不同ESM侦察设备下的被截获距离折算。

试验场景4：以上场景的组合。 实际试验中，用到了两种场景的组合，为主瓣ESM 侦察设备和副瓣ESM 侦察设备为不同设备，截获接收机灵敏度分别为Sm、Sl，进行主瓣被截获距离Rm和副瓣被截获距离Rl折算。

转换成常用的dB 表达式为：

式中，Ls_dB为副瓣电平，单位dB。

当考虑大气衰减时，等效模型为：

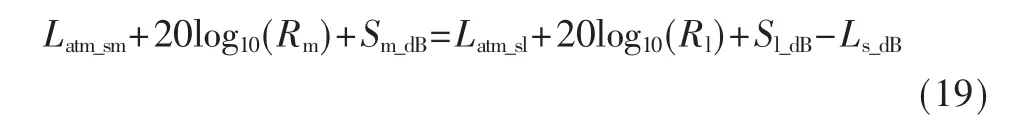
式中，Latm_sm和Latm_sl分别为主瓣和副瓣的大气衰减。 展开后，可得：

式中，γo和γw分别为干燥空气的吸收衰减率及水汽的吸收衰减率，均和水汽密度、温度、气压、频率有关。

2 模型验证

验证中，需要进行多次真实试验，修正替代模型的参数，待模型稳定后，可作为期望试验的被截获距离计算依据。 具体的实施步骤如下。

(1)根据指标的理论推导公式，建立等效模型；

(2)开展多次真实试验，任取两次试验，得到试验1的真实被截获距离和试验2 的真实被截获距离；

(3)在等效模型中代入试验1 的真实被截获距离，试验1 的被试和配试设备参数，试验2 的被试和配试设备参数，推导得到试验2 的等效被截获距离；

(4)将试验2 的真实被截获距离和试验2 的等效被截获距离对比，得到等效模型误差；

(5)根据等效模型误差，迭代修改等效模型参数，减小等效模型误差；

(6)当等效模型误差满足用户需求时，停止迭代，固化等效模型参数；

(7)在等效模型中代入替代试验的真实被截获距离，替代试验的被试和配试设备参数，期望试验的被试和配试设备参数，推导得到期望试验的等效被截获距离。

某型雷达的外场被截获距离的处理数据如表1 所示。

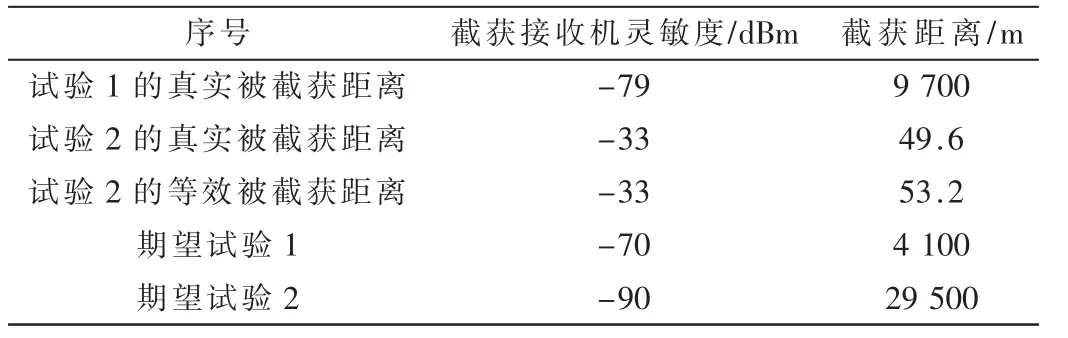
表1 被截获距离

验证不考虑大气衰减和考虑大气衰减的对比情况。 副瓣电平Ls_dB取-10 dB，大气衰减率γ=(γo+γw)=0.02 dB/km。主瓣被截获距离的验证结果如表2 所示。

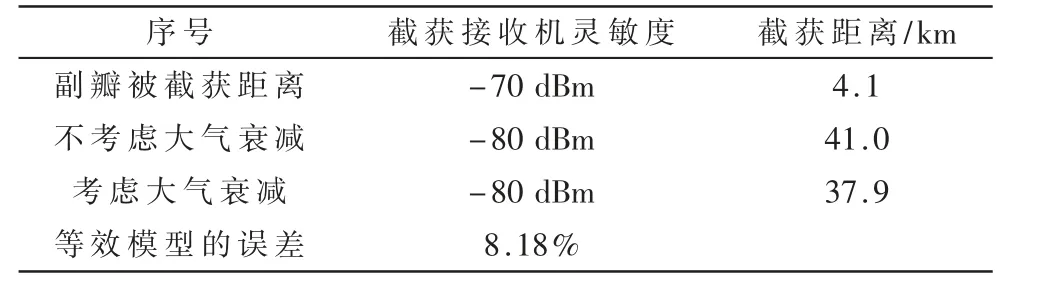
表2 有无大气衰减的对比情况

试验1 数据的试验场景是前文描述的“替代试验”，在空中试飞开展，被试飞机平台和挂载ESM 侦察设备的配试飞机相向飞行，随着距离的抵近，在9.7 km 时，到达临界截获状态。试验2 数据的试验场景同样是前文描述的“替代试验”，在机场地面开展，被试飞机平台和车载ESM 侦察设备相距49.6 m， 通过调节ESM 侦察设备的前端衰减器，等效降低其灵敏度，达到临界截获状态。 试验3 和试验4 的数据是通过试验1 和试验2 数据固化等效模型参数后，将截获接收机灵敏度代入等效模型，得到被截获距离。

通过试验2 的真实被截获距离和试验2 的等效被截获距离核算可以得到等效模型误差为7.26%，小于试验大纲要求的10%，满足固化等效模型参数的要求。 将期望试验1 和期望试验2 的截获接收机灵敏度代入等效模型后，可分别得到被截获距离为4.1 km 和29.5 km。

3 结论

本文研究的雷达被截获距离的等效模型方法已应用于某型雷达的低截获性能评估和鉴定考核中。利用了机场地面和空中试飞的多次试验数据，通过迭代优化的方式，建立了被截获距离的等效模型。 被截获距离等效模型的正确性、可行性已在实际试验中得到了初步的检验。 等效模型具有一定的通用性，可推广应用于数据链等射频信号的被截获距离测试。在等效模型的推导过用中， 各种系统损耗和大气衰减需要准确测算和标定，必要时需要单独进行建模和验证。 下一步，需要在更多的试验实践中进行数据积累，完善等效模型，提高模型的准确度。