基于聚类的密码芯片频域侧信道分析
蔡爵嵩,严迎建,朱春生,郭朋飞
(战略支援部队信息工程大学,河南 郑州450002)
0 引言
侧信道分析(Side-channel Analysis,SCA)是一种不仅利用算法本身,更依赖于密码算法物理实现中的侧信道泄漏的分析方法,严重威胁到密码芯片的安全性。 能量分析是一种最流行的侧信道分析方式,包括简单能量分析(Simple Power Analysis,SPA)[1]、差分能量分析(Differential Power Analysis,DPA)[2]、模板攻击(Template Attacks,TA)[3]、相关能量分析(Correlation Power Analysis,CPA)[4]等。现有文献主要是针对密码芯片的能量消耗在时域上进行分析。 但时域分析有一定的局限性,如能量迹的对齐问题。通常采集设备的不稳定或者芯片加入时钟随机化防护措施,都会导致能量迹需要进行对齐处理。因此,能量迹的对齐成为影响侧信道分析成功率的关键因素之一。
密码芯片有效信号的频率由时钟频率决定,不会受到采集设备和手段的影响,所以使用有效信号的频率能量大小代替能量迹采样点的功耗大小作为密钥的特征是可行的。 2000 年,AIGNER M 等人表示在对密码芯片侧信道分析中,时域内的能量消耗差异在频域内同样会体 现 出 来[5]。 2005 年,GEBOTYS C H 等 人 在CHES 会 议上通过对电磁信号的频域进行分析首次验证了频域侧信道分析的可行性[6]。 近年来,将能量迹转换到频域进行侧信道分析已经被证明是一种解决能量迹对齐问题的有效途径[7-9]。 虽然频域侧信道分析能够解决时域侧信道分析的对齐问题,但由于噪声频率可能与有效信号频率相同或相近,因此频域侧信道分析通常需要更多的能量迹,如文献[7]采集了70 000 条能量迹,文献[8]采集了10 000 条能量迹。
文献[10]~[14]表明将机器学习引入侧信道分析,能够有效找到能量迹上的特征点,提高侧信道分析的成功率。2017 年,ZHANG R N 等人[14]直接使用机器学习中的无监督学习算法k-means 对时域内的能量迹进行了分析,并成功获得其密钥。 本文将机器学习中的聚类算法引入频域侧信道分析中,寻找信号频率内在的分布,对有效信号频率进行分离,从而减少频域侧信道分析所用能量迹条数。
1 基础知识
1.1 相关能量分析(CPA)
2004 年,BRIER E 等人提出了相关能量分析(Correlation Power Analysis,CPA)[4],工作原理是基于芯片能量消耗W 与中间值模型H 之间具有线性相关性。 通过计算W 与H 之间的皮尔逊相关系数ρ(W,H)来评估中间值模型与实际能量消耗的匹配程度。
一般地,分析者采用的中间值模型为汉明重量模型(Hamming Weight,HW)或汉明距离模型(Hamming Distance,HD)。 分析者通过计算猜测密钥对应的中间值与芯片实际能量消耗之间的相关系数来进行分析,相关系数最大的对应密钥值即被认为是正确密钥。
1.2 频域侧信道分析
密码芯片的频域侧信道分析就是对傅里叶变换后的能量迹进行分析。由于能量迹是由采集设备采样得到的数字信号,在时域内是离散的有限时间序列,因此本文采用的是离散傅里叶变换(Discrete Fourier Transform,DFT)。
一般地,信号的时域波形表示信号随时间的变化,而其频域图则显示了在一个频率范围内每个给定频带内的信号量,所以频域内的信息更集中。 这也是频域侧信道分析一般需要比时域侧信道分析更多的能量迹条数的原因。
1.3 k-means 算法
机器学习中的无监督聚类算法可以利用样本数据内在的相似性对样本数据进行自动分类。将每一类称为一个簇,则有簇内相似性高、簇间相似性低的特点。本文选取应用最广、算法实现最简单的k-means 算法进行聚类分析。
给定样本集D={x1,x2,…,xm},k-means 算法从中选择k 个样本作为初始聚类中心{μ1,μ2,…,μk},计算样本xj(1≤j≤m)与各初始聚类中心μi(1≤i≤k)之间的距离:根据距离最近的聚类中心确定样本xj的簇标记λj(1≤j≤m):



1.4 轮廓系数(Silhouette Coefficient)
1986 年,ROUSSEEUW J 等人提出了轮廓系数(Silhouette Coefficient)[15],用来衡量一个点与它所属聚类类别的相似程度,可以用来在相同数据的基础上来评价不同算法或者算法不同参数对聚类结果产生的影响。
(1)计算样本xj(1≤j≤m)到同一簇Cλj内其他样本的平均距离aj。 aj越小,表明样本xj越应该被聚类到该簇。aj被称为样本xj的簇内不相似度。
(2)计算样本xj到其他簇Ci(i=1,2,…,k;i≠j)内所有样本的平均距离bij,称之为样本xj与簇Ci(i=1,2,…,k;i≠j)的不相似度,即样本xj的簇间不相似度。

bj为 样 本xj到 其 他 簇Ci(i=1,2,…,k;i ≠j)内 所 有样本的最小平均距离。可以知道,bj越大,说明样本xj越不属于其他簇Ci(i=1,2,…,k;i≠j)。
(3)根据样本xj的簇内不相似度aj和簇间不相似度bj,就可以定义样本xj的轮廓系数Sj:

容易知道,-1≤Sj≤1,当Sj越接近于1 时,簇内越紧凑,簇间越稀疏,聚类效果越优。所有样本的轮廓系数Sj的均值为聚类结果的轮廓系数,是评价该聚类是否合理、有效的指标之一。
2 基于聚类的频域侧信道分析
2.1 使用聚类算法分离有效信号的可行性分析
现在来分析能量迹中的有效信号与噪声信号相似度是否较低,即能否在能量迹中有效分离出有效信号。 设能量迹中某一点的信噪比(Signal to Noise Ratio,SNR)为:

其中,Pexp为侧信道分析所利用的有效信号能量,Psw.noise为转换噪声,Pel.noise为电子噪声。 显而易见,SNR 越高,从全部信号分离出Pexp越容易。一般地,在采集密码芯片能量消耗时通过低通滤波技术来提高能量迹的SNR,确保侧信道分析能够成功。 因此,对于一个能够成功进行频域侧信道分析的能量迹来说,Pexp是能够从全部信号中分离出来的。
本文的研究是在能够成功实施频域侧信道分析的前提下进行的,所以有效信号Pexp是能够从全部信号中分离出来的。 由于噪声频率和有效信号频率均为基频的倍数,因此,将能量迹进行傅里叶变换后,有效信号的频率与大部分噪声信号的频率的相似度低,只有很小一部分噪声与有效信号同频或频率接近,但这并不妨碍进行侧信道分析。 因此,使用聚类算法能够有效分离出有效信号的频率。
2.2 基于聚类的频域侧信道分析方法
结合频域侧信道分析方法和聚类算法,本文提出基于聚类的频域侧信道分析方法,流程图如图1 所示。 现给出该方法的具体实施步骤:
(1)使用采集设备对密码芯片能量消耗进行采集,得到n 条能量迹ti(i=1,2,…,n),组成能量迹集T={t1,t2,t3,…,tn}。
(2)对能量迹集T={t1,t2,t3,…,tn}中的每一条能量迹ti(i=1,2,…,n)进行离散傅里叶变换(DFT),得到:

(3)对T′使用k-means 算法进行聚类。 k-means 算法非常简单且使用广泛,运行速度快,可用于处理大型的数据集。 但该算法存在对初始参数比较敏感,需要找到相似程度低的类别才能进行较好的聚类。
由于只存在有效信号频率和噪声频率,因此聚类类别数设置为2。
(4)由于能量迹中噪声频率分布更广,有效信号频率占比较少,因此选择其中簇内数量较少的一类进行侧信道分析, 一般采用1.1 节所描述的相关能量分析(CPA)方法进行侧信道分析。
(5)如果失败,则回到步骤(3)。 因为聚类算法是根据数据内在特征进行自动分类,所以有可能会出现无法得到预期结果的情况。因此,在失败时,应该重新进行聚类分析,或者在对聚类算法进行优化改进[16]。
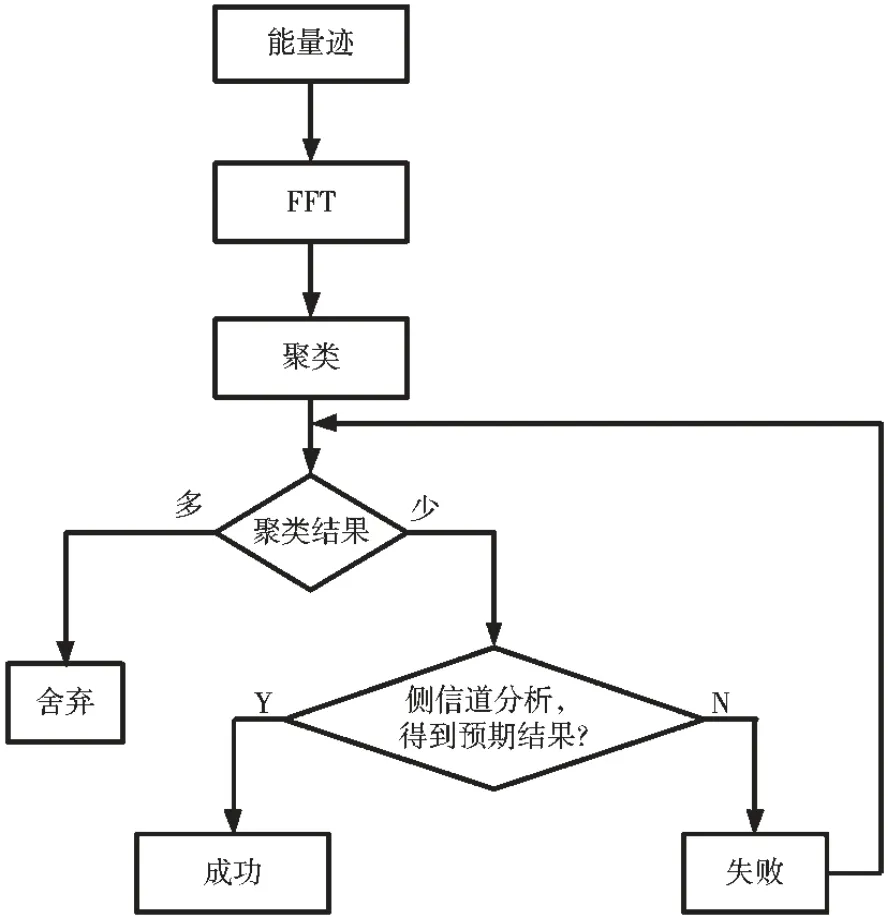
图1 基于聚类的频域侧信道分析方法流程图
3 实验验证及分析
本文使用ChipWhisperer 系列侧信道分析开发板[17]进行实验,验证基于聚类的密码芯片频域侧信道分析方法的可行性。
3.1 实验数据采集
本节使用CW1173 ChipWhisperer-Lite 开发板[18]进行能量迹采集,目标设备为ATMEGA XMEGA128,密码算法为128 位AES 算法, 共采集60 000 条能量迹用作分析。 实验平台为MATLAB R2018b,傅里叶变换使用的是MATLAB 自带的fft 和fftshift 函数。
图2 为AES 算法第一轮的能量迹曲线,图3 为经过傅里叶变换后的频域幅值谱。

图2 AES 算法第1 轮能量迹曲线

图3 AES 第1 轮能量迹经过傅里叶变换后的频域幅值谱
3.2 实验过程及结果
对AES 算法前4 轮分别进行傅里叶变换后,利用1.1节描述的相关能量分析(CPA)方法进行分析,中间值模型选择为S 盒输出的汉明重量(HW)值,然后计算中间值模型与傅里叶变换后的能量迹之间的相关系数。当连续使用多条能量迹进行分析得到的最大相关系数对应的猜测密钥值key_guess 不变时,即认为是正确密钥。
采取对比实验,设定3 组实验,第1 组为全部能量迹,第2 组为聚类后数量较多的能量迹,第3 组为聚类后数量较少的能量迹,分别记为I、II、III。 在实验中,将第I 组作为基准,第II 组和第III 组都与第I 组进行比较,看本文方法是否会减少能量迹条数,同时第II 组与第III 组进行比较,看本文方法是否能够准确分离出有效信号频率,结果如表1 所示。 其中,表内失败是指使用60 000 条能量迹无法分析得到正确密钥;表1 结果为最少所需能量迹条数;由于聚类算法是根据数据内在特征进行自动分类,因此会出现结果与表1 结果不一致的情况。
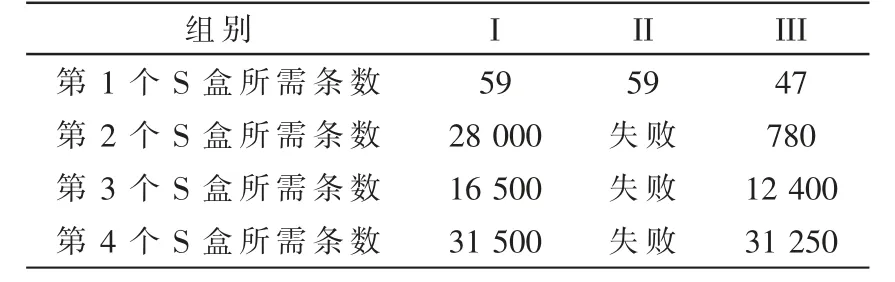
表1 3 组实验分析成功所需能量迹条数
3.3 实验结果分析
本文引入1.4 节介绍的轮廓系数(Silhouette Coefficient)对聚类算法参数设置和聚类后的结果进行评价。图4~图7 分别对应AES 算法第一轮的第1 个S 盒、第2个S 盒、第3 个S 盒、第4 个S 盒聚类后的轮廓系数图。

图4 AES 算法第一轮第1 个S 盒聚类后轮廓系数示意图
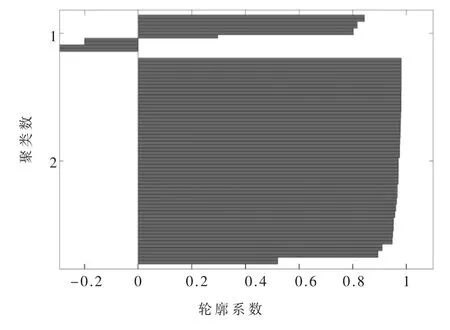
图5 AES 算法第一轮第2 个S 盒聚类后轮廓系数示意图
从图4~图7 可以看出,4 次聚类后的轮廓系数均接近1,说明文中聚类参数设置合理、有效,聚类效果较好,进一步说明本文所提方法的步骤(3)将聚类类别设为2 是正确的,同时表明通过聚类算法能够从全部信号中分离出有效信号。

图6 AES 算法第一轮第3 个S 盒聚类后轮廓系数示意图
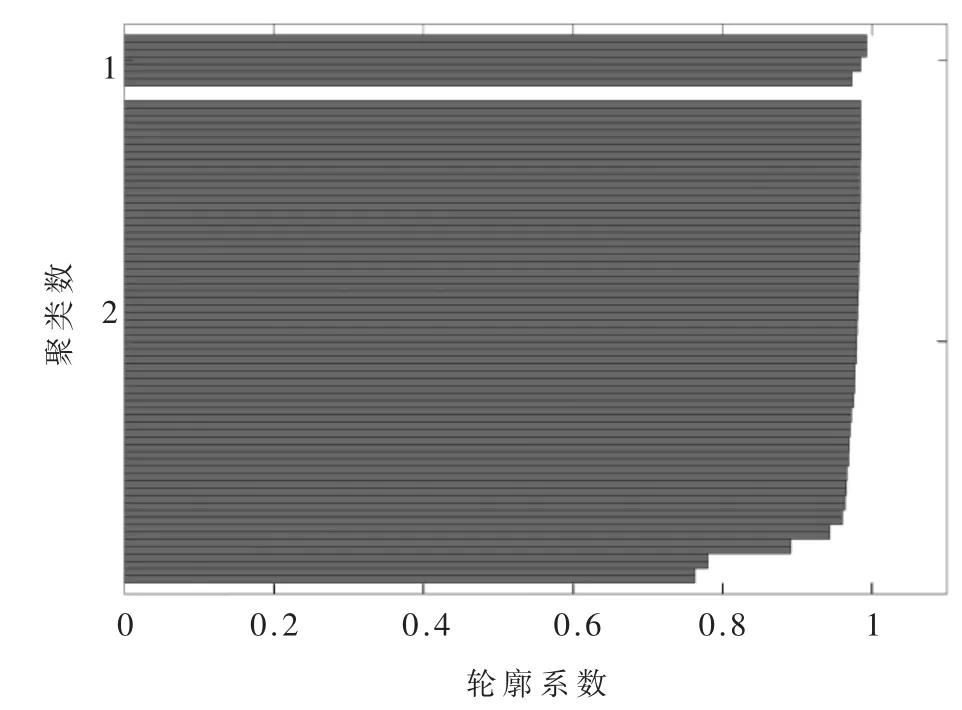
图7 AES 算法第一轮第4 个S 盒聚类后轮廓系数示意图
通过对表1 的分析可知,第III 组分析成功所需能量迹条数明显少于第I 组和第II 组,并且第II 组还存在不能成功分析的情况,说明能量迹中的有效信号频率确实在第III 组当中,即能准确分离出有效信号频率,从而进行有效侧信道分析,减少频域侧信道分析所需能量迹条数。
4 结论
将密码芯片的能量消耗转换到频域进行侧信道分析,能够有效解决能量迹对齐问题,但由于频域内的一个点对应时域内的多个点,因此频域侧信道分析往往需要更多的能量迹条数。 本文针对这个问题,提出使用机器学习中的聚类算法找出有效信号的频率后进行分析。实验结果表明,本文方法能够减少密码芯片频域侧信道分析所需的能量迹条数。将本文方法应用于密码芯片频域侧信道分析中,能够提高分析性能,使频域侧信道分析更加实用。

