基于深度学习的偏微分方程求解方法

毛超利

（中国电子科技南湖研究院，浙江 嘉兴 314002）

0 引言

伴随着计算机技术的高速发展，科学计算已经成为可与理论和实验科学方法相并列的第三种科学方法[1][2]。科学计算中的一个重要内容是数值求解各类偏微分方程（组）[3]。 数值求解偏微分方程（组）具有重要意义。 比如，核爆炸物理过程和流体宏观流动均可用偏微分方程组来描述，借助理论手段解析地求解这些偏微分方程，在当今数学发展水平下依然不可能[4]，利用科学计算方法求取它们的数值逼近解，可以补充试验无法得到的细节，从而利于减少试验次数、节约研发成本和缩短研发周期。 有资料表明[1]，从开始研制至原子弹爆炸成功，我国进行了338 次核试验，而美国、苏联分别进行了936次和716 次试验，其中一个重要原因是我国科学家充分采用了基于科学计算方法求解偏微分方程的数值模拟手段。

数值求解偏微分方程的算法包括有限差分法、有限体积法、有限元法和谱方法。 有限差分法是用差商近似代替微分[2]，从而将连续的偏微分方程转化为代数方程进行求解。有限体积法是将空间离散为结构化网格[2]，在每个网格内施加守恒定律，从而将全局的偏微分方程转化为局部代数方程进行求解。有限元法是把原来待求解的几何空间划分为有限元，并假设每个有限元上的原函数关系可以近似地由一组基函数进行线性组合，将该线性组合带入原偏微分方程，会有一个误差余量，通过引入加权函数将误差余量最小化，就可以得到一个线性方程组，对其求解即可得到原偏微分方程的数值解[5]。谱方法与有限元法类似，不同之处在于，谱方法是在全局时空上构造原函数基于基函数的线性组合[6]。以上四种方法均已得到充足的发展。 但是，它们各自有着一些无法克服的缺点。 比如，有限差分法会引入人工粘性。

近些年来，随着深度学习在众多实际应用中取得成功，越来越多的研究人员开始尝试利用它来解决各自领域的传统难题[7-9]。 受此启发，针对偏微分方程数值求解问题，本文尝试了一种新思路——基于深度学习的方法。该方法与有限元法和谱方法类似，都是对偏微分方程真实解对应非线性关系的一种数值逼近。 不同之处在于，有限元方法和谱方法是一次输入对应一次输出的单一映射，而在本文方法中，一层神经网络的输出又是下一层神经网络的输入，因此具有更强的非线性拟合能力。

1 基于深度学习的偏微分方程求解算法介绍

1.1 深度神经网络

前馈深度神经网络是最基础的神经网络，由输入层、隐藏层和输出层构成，信息由输入层向输出层单向传播。输入层和输出层一般具有单层神经网络，隐藏层可具有多层神经网络，每一层神经网络由若干个神经元构成。 在整个神经网络中，如果任意一层神经网络的任意一个神经元和下一层神经网络的所有神经元都是连接的，则称这种神经网络是全连接的[10]。 本文使用的就是这种前馈全连接神经网络，如图1 所示。

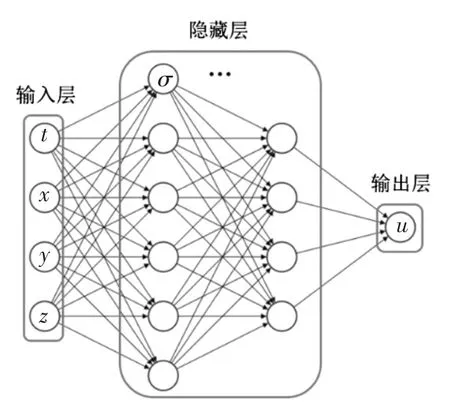
图1 神经网络示意图Figure 1 Schematic diagram of neural network

隐藏层内的每个神经元都包含一个激活函数（Activation Function）。 激活函数是简单的连续函数[10]，比如，三角函数中的双曲正弦函数、双曲正切函数等。本文选取双曲正切函数作为激活函数，如式（1）所示。

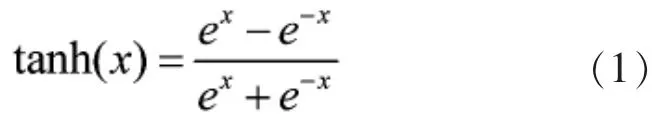
通常，隐藏层内的所有神经元包含同一形式的激活函数。将与隐藏层某一神经元连接的其他神经元传输进来的信息进行加权（weighted）平均，再加上一个偏置（bias），作为该神经元的输入，在激活函数的作用下，该神经元输出信息，并传递给下一层神经元。

用矩阵的形式表达，隐藏层的第一层接收到的信息如式（2）所示。

式（3）分别代表输入层作用于隐藏层第一层的权重系数矩阵和输入信息向量。在激活函数的作用下，隐藏层第一层神经元的输出信息如式（4）所示。

其中：σ 代表激活函数，B1代表该层神经元的偏置向量。对于图1 所示包含两个隐藏层的神经网络，信息经过过滤，到达输出层时，如式（5）所示。

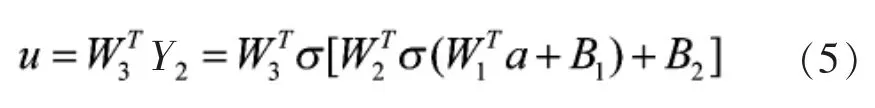
其中，W3∈R4×1是隐藏层第二层向输出层传递时的权重系数矩阵。 可以看到，最终的输出信息是关于输入信息和一系列权重系数以及偏置的复杂非线性关系。 选取合适的权重系数和偏置，则由神经网络表示的非线性关系是对原偏微分方程解的一个近似。

1.2 本文方法基本框架

为了讨论的方便，不失一般性地，本文考虑如下形式的二阶偏微分方程，如式（6）所示。

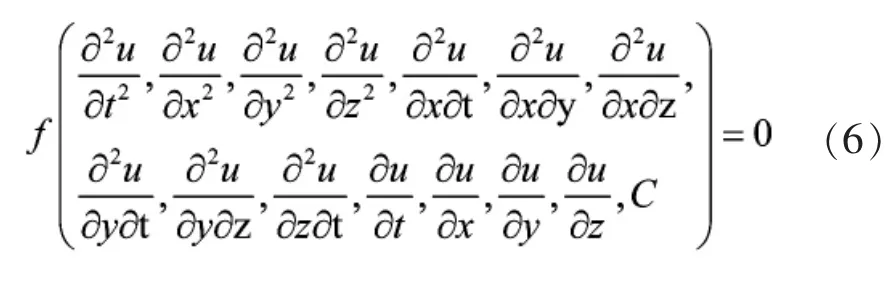
其中，C 代表任意常数项。 给定初始条件，或边界条件，或混合条件（初始条件加上边界条件），偏微分方程的解是唯一确定的。 其次，假设使用图1 所示的神经网络对上述偏微分方程的解进行逼近，则：

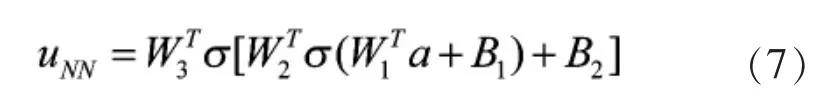
其中，右边项中的参数符号意义与第1.1 节保持一致，a=[t，x，y，z]T是输入信息向量。 一方面，由于uNN不是偏微分方程的精确解，故将其代入原偏微分方程左端时，结果不等于0，而是有一个余量偏差 Rf，如式（8）所示。

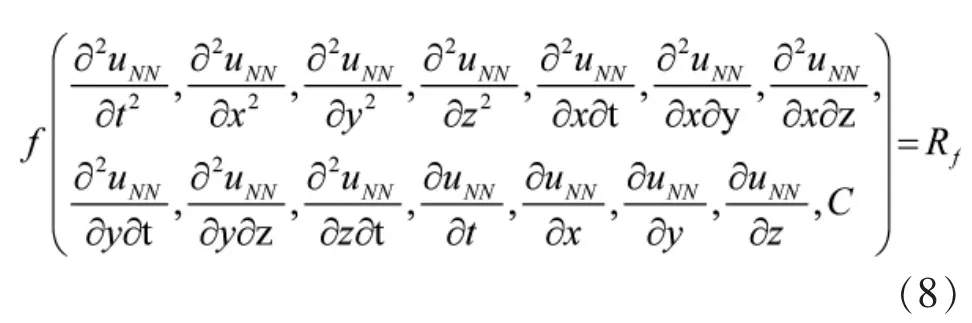
这里需要指出的是，在深度神经网络中，输出信息关于输入信息的偏微分可以使用自动微分（Auto-difference）计算，自动微分本质上是求导链式法则，具有很高的效率。另一方面，对应初始时刻的输出信息与初始条件的余量偏差Ri为：

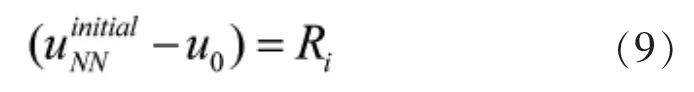
在求解域上均匀分布的一系列时空坐标下，取值最小。 其中，Nx，Ny，Nz和 Nt分别是计算域在 x，y，z 和 t 方向上的离散点个数，NxΓ，NyΓ，NzΓ分别代表计算域在x，y，z 边界上的离散点个数。 选取偏差余量的平方和作为准则的依据与最小二乘法的依据类似，具体细节可以参考相关文献[5]。 式（11）即是基于深度学习偏微分方程求解算法的最小化目标函数， 它可以看作是关于一系列权重系数W 和偏置B 的函数，即：

因此，偏微分方程求解问题最终转化为一个无约束最优化问题。求解无约束最优化问题常用的数值算法有梯度下降法[11]、拟牛顿算法BFGS[12]等。 拟牛顿算法BFGS 本质上是从梯度下降法开始迭代，不断逼近牛顿法求曲线驻点的算法，其效率比梯度下降法高。 经过研究人员的不断改进，L-BFGS 算法[12]进一步克服了原始的BFGS 算法内存需求大的缺点。 因此，本文采用L-BFGS 算法求解由偏微分方程求解转化而来的无约束最优化问题。 综上所述，本文基于深度学习的偏微分方程求解算法基本框架如图2 所示。

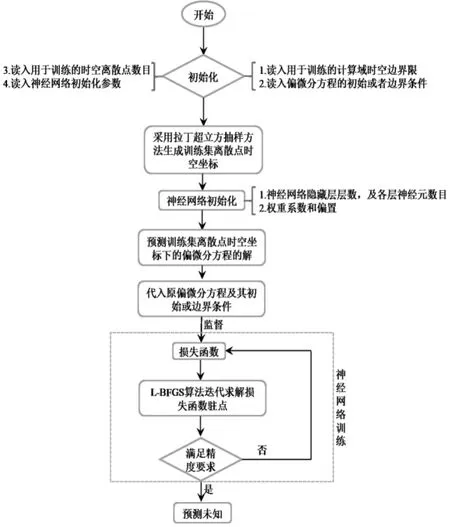
图2 算法流程图Figure 2 Algorithm flow chart

2 算法验证

从数学角度， 偏微分方程可以分为椭圆型方程、双曲型方程和抛物型方程[3]。本文选取对应这种分类的三个算例对算法进行验证。

2.1 一维对流方程的初值问题

一维对流方程是典型的一阶双曲型偏微分方程，具有如下形式：

其中，a 是非零常数。 我们知道， 它是双曲型的，给定初始条件，它的解是唯一的。

不失一般性地，这里令a=-1，并给定如下初始条件：

初始信号是三角形的，宽度为0.2，且在x=0 处一阶导数不连续。 为了检验本文算法准确性，分别采用本文算法和有限差分迎风格式算法求解上述双曲型偏微分方程的初值问题。不同时刻的结果如图3 所示。

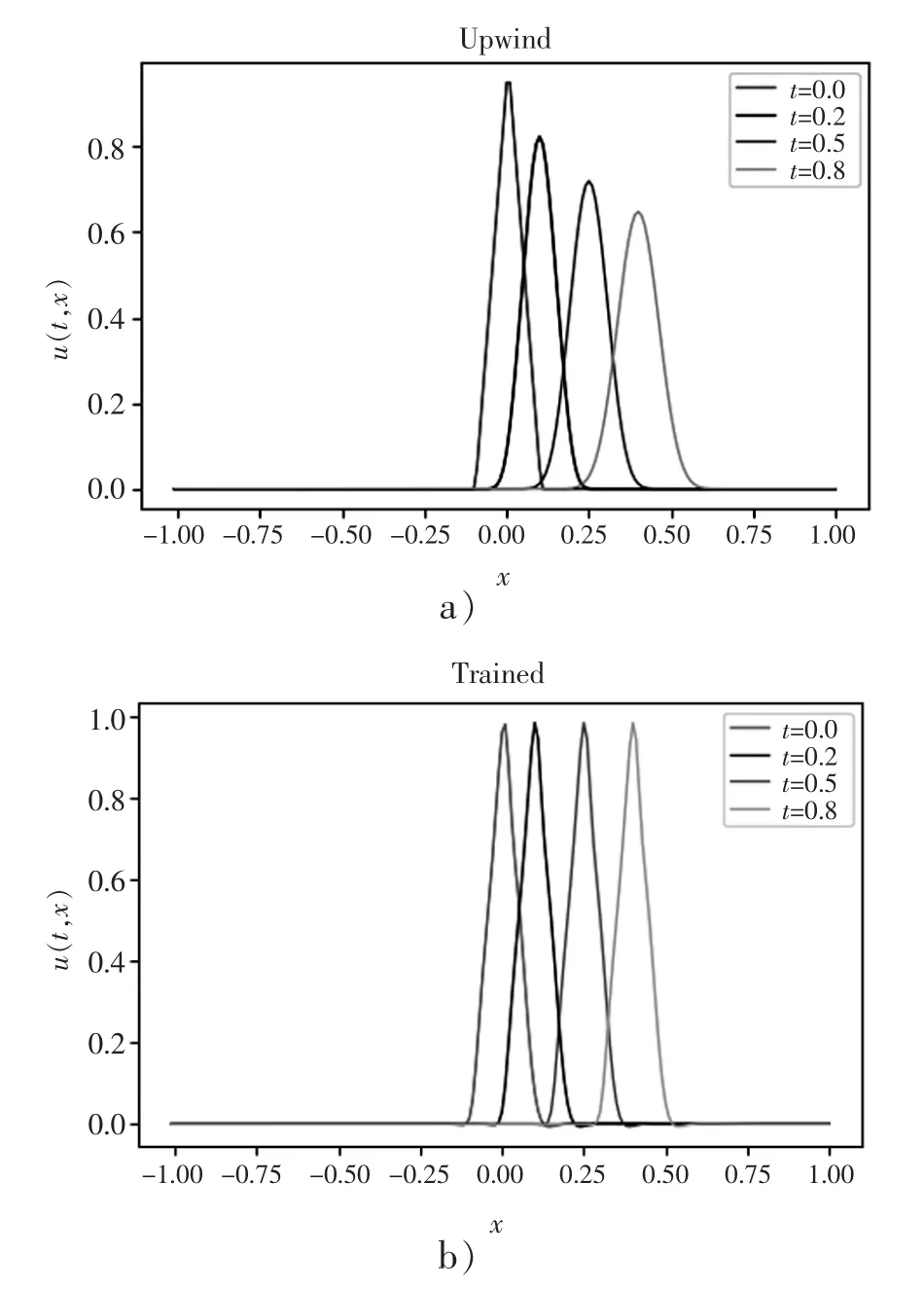
图3 采用迎风格式算法和本文深度学习算法计算结果对比Figure 3 Comparison of calculation results using upwind style and deep learning algorithm

理想情况下，求解的结果应该是在不同时刻分布在不同空间位置的三角形信号形状。从图3 可以看到，由于引入了“人工粘性”[2]，迎风格式“抹平”了信号尖角，而且随着时间的演化，信号强度也被削弱。 相比之下，本文基于深度学习算法的结果较好地保持了初始信号的形状和强度。

2.2 二维拉普拉斯方程的边值问题

二维拉普拉斯方程是典型的椭圆型偏微分方程，不失一般性地，这里假设它具有如下形式：

从物理角度， 该方程描述的是一个稳态现象，比如在边界温度给定的条件下，一块金属平板内部温度的分布。椭圆型偏微分方程的边界条件有以下三种提法：（1）固定边界条件，即在给定边界上给定u 的值 U1（x，y）；（2）在给定边界上给定 u 的法向导数值，=U2（x，y）；（3）在给定边界上给定混合边界条件，+u=U3（x，y）。 其中，第一种提法最为普遍， 本小节以第一种提法对算法进行验证。 给定如下计算域边界以及边界条件：

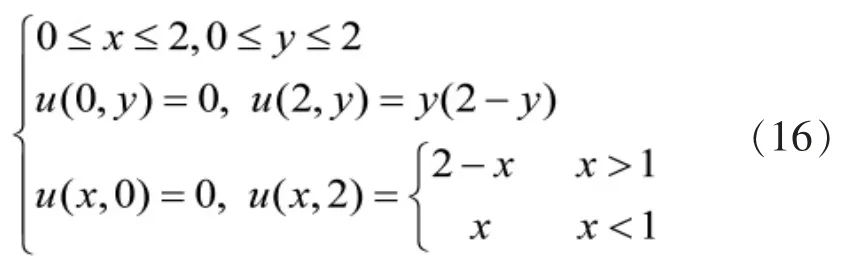
分别采用本文算法和五点差分格式求解。整体分布云图定性对比和不同位置处的结果定量对比如图4 所示。 可以看到，本文算法与五点差分格式具有相当的精度。

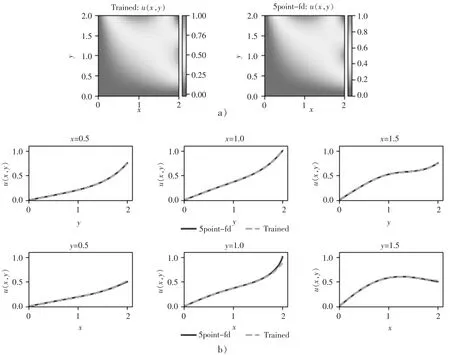
图4 二维拉普拉斯方程数值解结果Figure 4 Numerical solution results of the two-dimensional Laplace equation

更进一步地，本小节探讨深度神经网络隐藏层层数和宽度（每层的神经元数目）对计算结果的影响。 相对误差百分比的计算选取五点差分格式结果作为精确解。 结果如表1 所示。 可以看出，对于二维拉普拉斯方程，随着隐藏层宽度的增加，神经网络预测精度大体上先上升后下降， 而随着隐藏层层数的增加， 预测精度大体上反而下降。 这说明， 使用神经网络预测二维拉普拉斯方程边值问题数值解时， 采用更多的神经元并不一定会带来预测精度的提升。

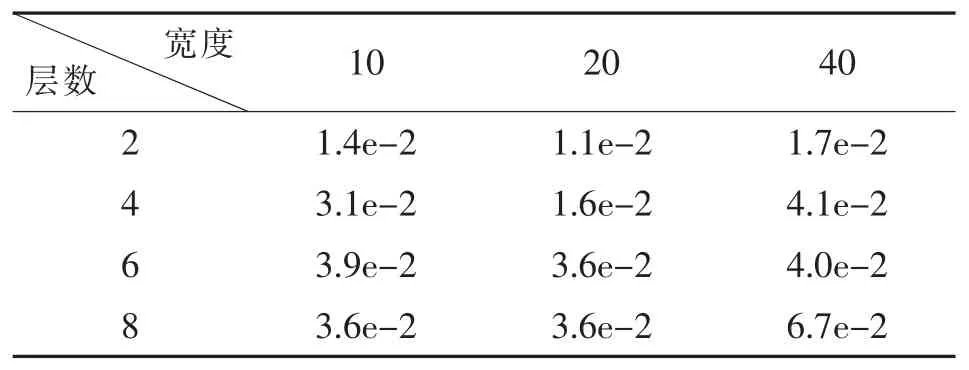
表1 二维拉普拉斯方程神经网络预测数值解的相对误差百分比Table 1 The relative error percentage of the twodimensional Laplace equation neural network predicting the numerical solution

2.3 一维扩散方程的初边值问题

扩散方程是应用中常见的抛物型偏微分方程，它有着明显的物理背景，例如不同浓度物质之间的扩散过程、热传递过程和波传播过程等。 如式（17）所示的偏微分方程：

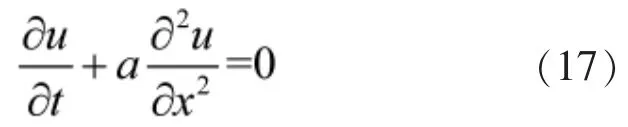
式（17）是典型形式的扩散方程。 其中，a 是非零常数。 给定初始和边界条件，上述偏微分方程有唯一解。

选取a=-1，并给定如下初始以及边界条件：

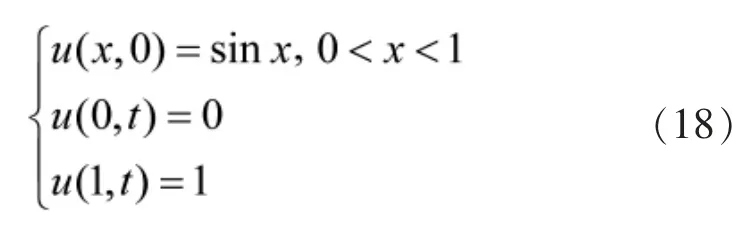
分别采用本文算法和Crank-Nicolson 格式求解。神经网络预测的整体分布云图和不同时刻的结果定量对比如图5 所示。 其中图5a）为神经网络预测值云图，白线标记定量对比的时刻。可以看到，本文算法与Crank-Nicolson 格式具有相当的精度。

图5 一维扩散方程数值解结果Figure 5 Numerical solution results of one-dimensional diffusion equation

更进一步地，本小节探讨深度神经网络隐藏层层数和宽度（每层的神经元数目）对计算结果的影响。相对误差百分比的计算选取Crank-Nicolson 格式结果作为精确解。结果如表2 所示。可以看出，类似于二维拉普拉斯方程结果， 对于一维扩散方程，随着隐藏层宽度的增加，神经网络预测精度大体上先上升后下降，而随着隐藏层层数的增加，预测精度大体上反而下降。 这说明，使用神经网络预测一维扩散方程初边值问题数值解时，采用更多的神经元并不一定会带来预测精度的提升。

3 结语

本文提出了一种基于深度学习的偏微分方程求解方法。 针对双曲型、椭圆型和抛物型偏微分方程三种典型问题，分别使用有限差分格式和本文方法进行求解。 结果对比表明，本文算法具有比较好的求解精度，而且它能够克服迎风格式引入人工粘性的缺点。 此外，本文算法不需要针对不同类型的偏微分方程作特殊处理，即本文算法框架具有更广泛的适用性。

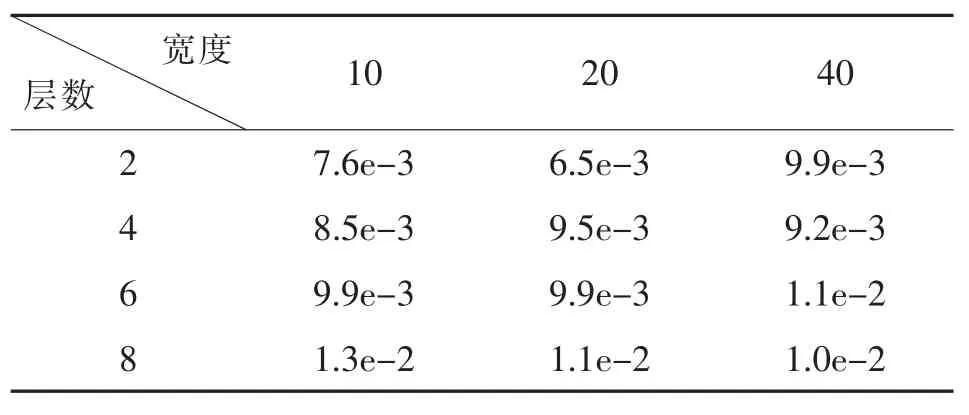
表2 一维扩散方程神经网络预测数值解的相对误差百分比Table 2 The relative error percentage of the onedimensional diffusion equation neural network predicting the numerical solution

本文方法的以上优点并不意味着目前它可以在工程应用中取代业已发展成熟的传统方法。原因是，基于深度神经网络求解偏微分方程时，误差规律还不清楚。 此外，使用深度学习方法求解偏微分方程要求问题的边界条件或初始条件有比较明确的定义，否则可能会出现边界捕捉不到或者瞬态求解不准确的问题。鉴于以上两个方面，未来，我们需要对训练过程中深度神经网络是如何收敛到偏微分方程解的数学本质进行深入研究。