基于功效系数法的采空区稳定性判别方法研究

何泽正，郭忠林，刘 林，胡建非，董 法

(昆明理工大学 国土资源工程学院，昆明 650093)

随着矿产资源的开采不断向地下发展，势必会在开采的过程中遗留大量采空区。采空区的长期存在对于矿山和地表构筑物构成一种潜在的安全隐患。近年来由于采空区失稳而造成经济损失和人员伤亡的事件时有发生。因此对采矿后遗留的采空区进行稳定性判别，为采空区防治提供科学依据，消除存在的安全隐患是十分必要的。

目前，国内外学者对采空区稳定性评价进行了大量的研究，取得了较多显著性成果。邓红卫等[1]针对采空区稳定性评价时的模糊性、随机性以及评价指标等级呈有限区间正态分布等问题，考虑评价指标值突变对评价指标权重的影响，提出了基于变权联系云的采空区稳定性二维评价模型，并在实际应用对该模型的可行性进行了验证。黄英华等[2]基于模糊数学理论和层次分析法建立了一种由因素集合、权重集合和评价集合组成的采空区稳定性评价指标体系。王路遥等[3]结合模糊综合分析评价理论与数值模拟研究手段，对采空区危险性进行了系统地分析与评价。孙宇超等[4]通过AHP和模糊数学方法建立了评价下向水平分层胶结充填法充填前采空区稳定性的评价模型，并对某矿山采空区进行稳定性判断。胡洪旺等[5]建立了BP神经网络层状矿床采空区稳定性评价模型，并通过实际运用验证了模型的可行性。徐晓鼎等[6]运用突变理论对各类采空区支撑系统稳定性进行分析，并对采空区的危险性进行了判别。王正帅等[7]基于模糊数学与可拓学，建立了模糊可拓评价模型用于评价老采空区的稳定性。

以上研究方法，对采空区的稳定性判别具有一定的指导意义，但是计算过程较为繁琐，有时需要借助计算机才能完成计算，不便于推广。功效系数法，具有计算简单、快速等优点，既可以进行手工计算，也可以利用计算机进行计算。

本文以某铜矿采空区为背景，为对采空区的稳定性进行客观正确的判别，提出了计算简单、客观性较强的采空区稳定性判别模型：变异系数法赋权-功效系数法采空区稳定性判别模型。同时建立数值模型对采空区的稳定性进行模拟分析，与提出的模型相互验证，最终对矿山采空区的稳定性做出了正确的判别。以期为采空区的稳定性判别提供新的思路。

1 工程概况

朱家坝铜矿是一座已经开采多年的老矿山，矿山在开采时主要使用全面法采矿，在长期的开采后形成了大量的采空区。目前矿山存在7个采空区，总面积为15.3 万m2，总体积为 58.58 万m3。为消除采空区带来的安全隐患，需要对这7个采空区进行稳定性判别，进而为采空区的治理提供依据。

2 判别模型构建

2.1 变异系数法基本原理

变异系数法是一种客观的赋权方法，通过当前值与目标值之间的变异程度来对指标进行赋权，当前值与目标值之间的差异越大则指标权重越大，差异越小则指标权重越小。

变异系数法赋权步骤如下：

1)假设有m个评价指标，n个待评样本，构建原始评价矩阵A：

(1)

式中：aij表示第i个样本，第j项评价指标的数值。

2)计算第j项评价指标的均值和标准差：

(2)

3)计算第j项评价指标的变异系数：

(3)

式中：vj为第j项指标的变异系数。

4)对变异系数进行归一化处理，得到各指标的权重：

(4)

计算得最终的指标权重：

W={w1，w2，…，wm}

(5)

2.2 功效系数法基本原理

功效系数法，是一种基于多目标规划原理建立的，可从复杂评价对象的多个侧面对评价对象进行评分的评价方法。功效系数法具有可对复杂对象评价、减少评价结果偏差的优点[8]。功效系数法的判别过程如下：

1)建立评价指标体系

在选择指标时，应选择能充分反映评价对象的特性，并且具有一定的独立性和互补性的指标，以这些指标建立评价指标体系。

2)确定评价指标的满意值和不允许值

满意值和不允许值指的是在各项指标参与评价时，评价指标可能会达到最高水平与不应该达到的最低水平。

3)计算单项功效值

评价指标与单项功效系数之间具有多种不同的关系，在功效系数法评价体系中根据二者之间不同的关系，将这些指标分为极大型指标、极小型指标、稳定型指标、区间型指标四类，各类型的指标计算公式如下：

(1)极大型指标：单项功效值与指标数值成正相关。

(6)

(2)极小型指标：单项功效值与指标数值成负相关。

(7)

(3)稳定型指标：指标数值在一数值时，单项功效系数最高。

(8)

(4)区间型指标：指标数值在一定区间内时，单项功效系数值最高。

(9)

式中：ε为单项功效系数值；xi为第i个指标的值；xsi、xni为第i个指的标满意值、不允许值；xmax、xmin为第i个区间型指标最大值、最小值；xnmax、xnmin为第i个区间型指标上限不允许值、下限不允许值。

4)计算各评价对象总功效系数值。

根据评价指标单项功效值和各指标的权重值，利用下式计算出评价对象总共效系数值：

(10)

式中：E为评价对象总功效系数值；m为评价指标个数；εi为第i个评价指标的单项功效系数值；ωi为第i个评价指标的权重值。

3 采空区稳定性分析

3.1 评价指标体系的构建

采空区的稳定性与多种因素有关，如岩体构造、地质结构、岩石抗压强度、水文因素、采空区形状、矿体倾角、暴露面积、采空区高度、采空区体积、埋藏深度、跨度、采动扰动情况等[9-11]。查阅大量文献，结合朱家坝铜矿采空区实际情况，选取了能充分反映采空区特征的采空区跨度、暴露面积、空区高度、空区埋深、矿柱尺寸等五个参数作为采空区稳定性判别的评价指标。并根据文献[12]中给出的采空区危险度结构尺寸效应分级标准表，以及黄英华在文献[2]中给出的采空区稳定性等级划分标准表，将采空区稳定性等级分为稳定、基本稳定、不稳定、极不稳定4级，构建采空区稳定性评价指标体系见表1。

3.2 确定评价指标的满意值和不允许值

评价指标的满意值和不允许值表示了评价指标可能达到的最高水平和不应达到的最低水平，所以对于极大型指标：跨度、暴露面积、高度、埋深，其满意值应为Ⅳ级对应的标准值，不允许值则为Ⅰ级对应的标准值；对于极小型指标：矿柱尺寸，其满意值为Ⅰ级对应的标准值，不允许值为Ⅳ对应的标准值，见表2。

表2 各评价指标满意值和不允许值

3.3 计算各指标的单项功效值

根据采空区调查报告，将朱家坝铜矿的1至7号采空区的各评价指标的实测值进行整理，见表3。

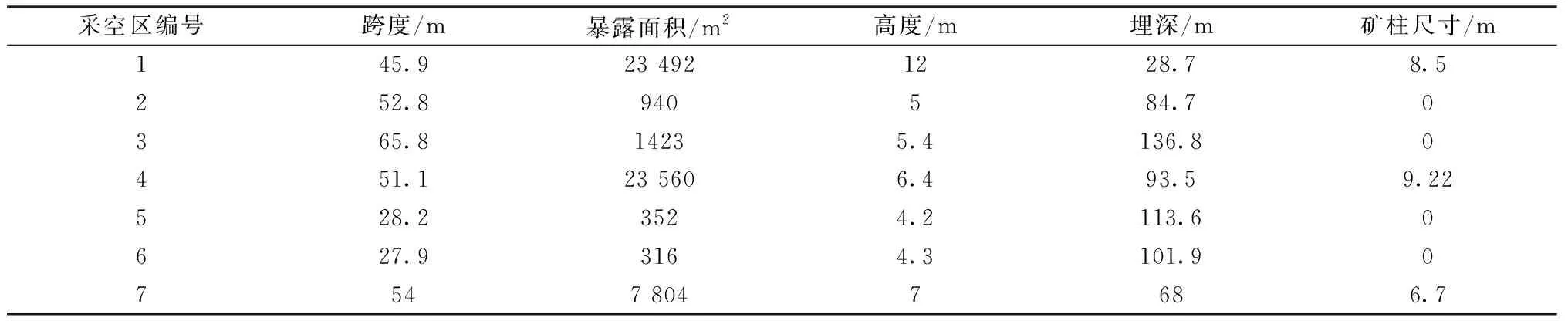
表3 各空区评价指标实测值

利用式(6)求出跨度、暴露面积、高度、埋深等极大型指标的单项功效值；利用式(7)求出矿柱等极小型指标的单项功效系数值，结果见表4。

表4 各指标单项功效值

3.4 计算各采空区指标的权重

1)由5个评价指标，7个采空区样本，构建原始评价矩阵A：

2)由式(2)计算出第j项评价指标的均值和表准差：

3)计算第j项评价指标的变异系数，由式(3)计算各指标的变异系数：

4)对变异系数进行归一化处理，得到各指标的权重，由式(4)计算各指标的权重：

3.5 计算各采空区总功效系数值

由式(10)计算各采空区的总功效系数值，见表5。

表5 各采空区总功效系数值

3.6 采空区稳定性判别

根据采空区稳定性评价指标体系以及各采空区的总功效系数值构建采空区稳定性判别表，见表6。

表6 采空区稳定性分级表

根据表5各采空区总功效系数和表6采空区稳定性分级表，对采空区的稳定性进行判别：1、7号采空区处于极不稳定的状态；2、3、4采空区处于不稳定的状态；5、6号采空区处于基本稳定的状态。

4 数值模拟验证

4.1 采空区稳定性判据

为验证判别模型的结果正确与否，根据采空区的地质资料构建出采空区的数值计算模型，并通过模拟，得到采空区围岩和矿柱可能的位移量。根据文献[13]给出的岩体位移量与岩体稳定性关系表，构建围岩变形量与采空区稳定性关系表7。

表7 围岩变形量和采空区稳定性的对应关系表

4.2 模型验证

根据矿山提供的地质剖面图、地表地形图建立的某矿山采空区模型长1 000 m、宽1 200 m、高644 m，采空区围岩主要为灰岩、板岩和白云岩，围岩及矿体的物理力学参数见表8。计算模型如图1所示。

图1 采空区模型Fig.1 Goaf model

表8 岩体力学参数

各采空区模拟计算结果如图2至图7所示。

图2 1号采空区位移Fig.2 No.1 goaf displacement

图3 2号采空区位移Fig.3 No.2 goaf displacement

图4 3号采空位移Fig.4 No.3 goaf displacement

图5 4号采空区位移Fig.5 No.4 goaf displacement

图6 5号采空区位移Fig.6 No.5 goaf displacement

图7 6号采空区位移Fig.7 No.6 goaf displacement

图8 7号采空区位移Fig.8 No.7 goaf displacement

由图2、5和8可知，1、4、7号采空区的最大位移分别约为204、272、355 mm，此时的采空区底部及矿柱的底部极容易发生破坏，使采空区失去稳定性，根据表7，采空区的最大位移>200 mm可以判断出采空区处于极不稳定的状态；由图3、4可知，2、3号采空区的最大位移分别为63、55 mm，采空区的底部易发生底鼓破坏，根据表7，2、3号采空区的位移处于50～100 mm之间，采空区处于不稳定的状态；由图6、7可知，5、6号采空区最大位移量约为96、80 mm，最大位移发生在采空区底部的岩体中，采空区的底板位移量较小均小于50 mm，采空区较为稳定，根据表7，5、6号采空区处于稳定或者基本稳定的状态。

对比判别模型与数值模拟分析结果，评判模型的结果与数值模拟结果基本一致，构建的变异系数法赋权-功效系数法采空区稳定性评价模型具有较好的可行性和适用性。

5 结论

1)采用变异系数法对各指标进行赋权，减少了主观因素的影响，使评判的结果更加客观。

2)建立变异系数法赋权-功效系数法采空区稳定性判别模型，对朱家坝铜矿的7个采空区稳定性进行判别：1、7号采空区处于极不稳定状态，2、3、4号采空区处于不稳定状态，5、6号采空区处于基本稳定状态。

3)通过对朱家坝铜矿的采空区进行数值模拟分析与计算，采用采空区围岩位移的计算结果对采空区的稳定性进行判别：1、4、7号采空区处于极不稳定状态，2、3号采空区处于稳定状态，5、6号采空区处于基本稳定或稳定状态，判别结果与所构建的评判模型结果一致，建立的评判模型具有较好的工程适用性。