危岩体断裂特性的网格重构数值仿真研究

程 静

(浙江同济科技职业学院水利工程学院，浙江 杭州 311231)

危岩体广泛存在于我国西部地区，其主控裂隙往往是影响其稳定性的重要因素。危岩致灾因素较多，如降雨、地震和自重作用等。危岩失稳灾害屡见不鲜，如2008年我国汶川地震，发生了邻近高速公路的危岩失稳下坠，导致多辆汽车被砸毁，造成了人员重大伤亡事故；2009年7月我国四川省汶川县国道213 线彻底关大桥发生了危岩失稳坠落，导致大桥断落，造成6人死亡、交通瘫痪，经济损失过亿元。因此，对危岩体在复杂工况下的稳定性进行分析是防治危岩失稳的关键所在。

针对危岩体的断裂力学模型分析方面，国内外学者进行了大量有益的研究工作。如王林峰等构建了危岩体的震动理论模型，对地震作用下危岩体的稳定性进行了分析；李部等对滑塌式危岩体的主控结构面断裂扩展方向和稳定性进行了理论分析；王景宏对链子崖危岩体的地质特性及其破坏机制进行了探讨；李克森等基于断裂力学与水力学理论对危岩体主控面断裂的渗流特性进行了分析研究。同时，相关规范也运用赤平极射投影及模糊数学建立了危岩体稳定性的评价标准。

但是以上研究不能实现危岩体裂纹扩展全过程的评价。随后人们利用各种方法对危岩体裂纹扩展过程进行了数值仿真研究，如陈洪凯等利用断裂力学理论对危岩体裂纹扩展过程进行了数值仿真研究，得到了危岩体裂纹扩展及应力强度因子的变化规律；郑安兴等利用扩展有限元对降雨及自重作用下危岩体断裂扩展过程进行了数值分析；陈鹏宇等利用离散元软件PFC对危岩体破坏过程进行了数值仿真研究。另外，还有诸如近场动力学法(PD)、数值流形法等，以上方法解决了部分问题，但是有些方法根本不是基于断裂力学理论，还有些方法使用起来具有诸多限制，如需要预设裂纹扩展路径，且编程复杂，难于推广使用。

鉴于以上研究的不足之处，本文基于Abaqus软件平台，利用Python语言开发了基于断裂力学理论的危岩体任意裂纹自由扩展的网络重构数值模拟方法，该方法利用围道积分计算每一步裂纹前缘的应力强度因子(SIF)，根据最大主应力法则判断危岩体裂纹的扩展方向，并利用网格重剖分技术实现了危岩体裂纹的扩展。基于以上网络重剖分数值模拟新方法对降雨条件下危岩体的断裂过程及应力变形规律进行评价，并对危岩体在不同裂纹长度及裂纹角度的断裂过程和应力变形规律进行敏感性分析，研究结果可为降雨条件下危岩体稳定性分析提供参考，同时可为降雨条件下危岩体任意裂纹扩展的数值仿真技术研究提供新的思路。

1 计算理论与数值手段

1. 1 围道积分计算危岩体裂纹尖端的应力强度因子

在准静态分析的背景下，

J

积分在二维中定义为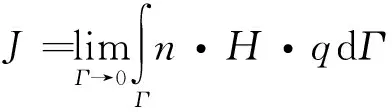

(1)

式中：

Γ

为从底部裂纹表面开始到顶部表面结束的轮廓，如图1(a)所示，

Γ

→0表明轮廓收缩到裂纹尖端;

q

为在虚拟裂纹扩展方向上是否存在单位向量；

n

为

Γ

的法线方向；

H

可以表达为下式：

(2)

其中：对于弹性材料，

W

定义为弹性应变能，对于弹塑性或弹黏塑性材料，

W

定义为弹性应变能密度加上塑性耗散，从而表示“等效弹性材料”中的应变能；

I

为刚度矩阵；

σ

为裂纹尖端的应力场；

u

为裂纹尖端的位移场；

x

为裂纹尖端的位置坐标。

J

积分可以表达为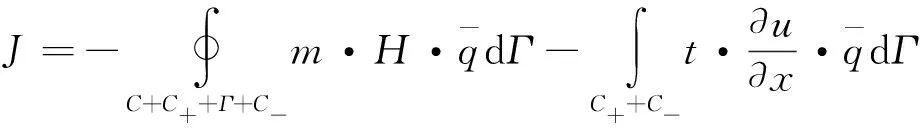

(3)

裂纹尖端应力强度因子在线性弹性断裂力学中起着重要的作用，它们描述了荷载或变形对裂纹尖端应力和应变场大小的影响，并测量了裂纹扩展倾向或裂纹驱动力。此外，裂纹尖端应力强度因子与能量释放速率(

J

积分)有关：

(4)

式中：

K

为裂纹尖端应力强度因子，

K

=[

K

,

K

,

K

]；

B

为前对数能量因子矩阵，对于均质、各向同性材料，

B

是对角阵。

因此公式(4)可以简化为

(5)

因此，公式(5)建立了

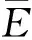
J

积分与裂纹尖端应力强度因子之间的关系，可以根据该式计算裂纹尖端的应力强度因子。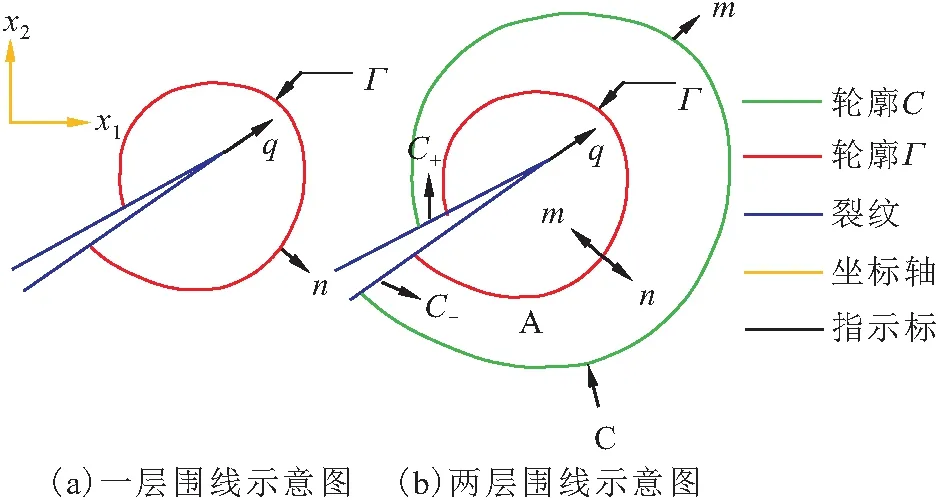

图1 裂纹尖端围线示意图Fig.1 Schematic diagram of the crack tip girth

1.2 基于网格重剖分的危岩体裂纹扩展数值方法

危岩体的裂纹扩展数值模拟方法在各种商业软件中均有内置，但是对裂纹扩展具有诸多限制，如需要预设裂纹扩展路径，无法真正意义上实现危岩体裂纹的任意扩展。同时，以往数值模拟方法多采用岩体损伤理论或者弹塑性理论，无法体现危岩体裂纹尖端的断裂力学特征。因此，本文基于围线积分及Abaqus平台实现了基于断裂力学的危岩体任意裂纹扩展，并利用Python语言实现了危岩体裂纹尖端应力强度因子提取、裂纹扩展准则判断、裂纹重构及网格重剖分等操作，可达到危岩体任意裂纹自由扩展的目的，同时可以真实地反映危岩体裂纹尖端的断裂力学特性。基于网络重剖分的危岩体裂纹扩展数值模拟方法流程图如图2，具体步骤如下：

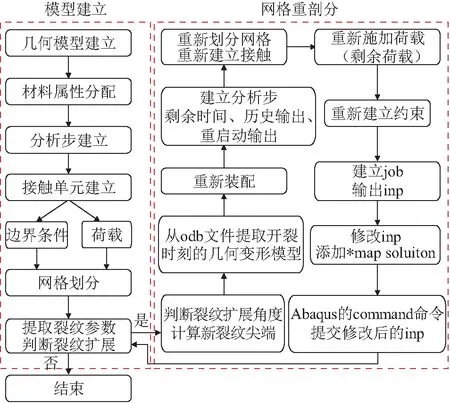
图2 基于网格重剖分的裂纹扩展数值方法流程图Fig.2 Flow chart of numerical method of crack propagation of dangerous rock mass based on grid reconstruction

(1) 建立初始裂纹模型，分配材料属性，建立Crack的历程输出，建立边界条件及荷载，划分网格。

(2) 对初始裂纹模型进行静力有限元计算，判断裂纹尖端的应力强度因子是否达到材料的断裂韧度，若达到材料的断裂韧度，则裂纹发生扩展，删除原始模型网格，裂纹往前扩展一个增量，重新划分网格。

(3) 利用Abaqus中的*map solution功能将前一步的模型映射到新一步模型的网格上，施加剩余荷载，进行下一步裂纹扩展。

1. 3 最大周向应力准则

危岩体的裂纹扩展需要解决裂纹扩展方向的判别问题。均质、各向同性线弹性材料的近裂纹尖端应力场可以表达为

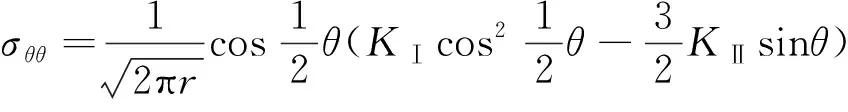
(6)

(7)

式中：

σ

为环向应力；

τ

为切向应力；

r

和

θ

为与裂纹前沿正交的平面上以裂纹尖端为中心的极坐标。

利用上述这两种条件都可以得到裂纹的扩展方向，即：

(8)

2 重庆市万州太白危岩体稳定性分析

2. 1 工程概况

本文以重庆市万州太白编号为W15的危岩体(见图3)为例，利用上述建立的危岩体任意裂纹扩展的网络重构数值模拟方法对该危岩体的稳定性进行数值仿真分析，以验证该方法的有效性。该地区多年平均降雨量为1 000 mm，对危岩体治理过程中发现，在2004年5月份由于暴雨导致了危岩体多处地方崩落，因此研究暴雨工况与不同裂隙赋存情况下危岩体的断裂特性对于防治危岩失稳灾害十分关键。

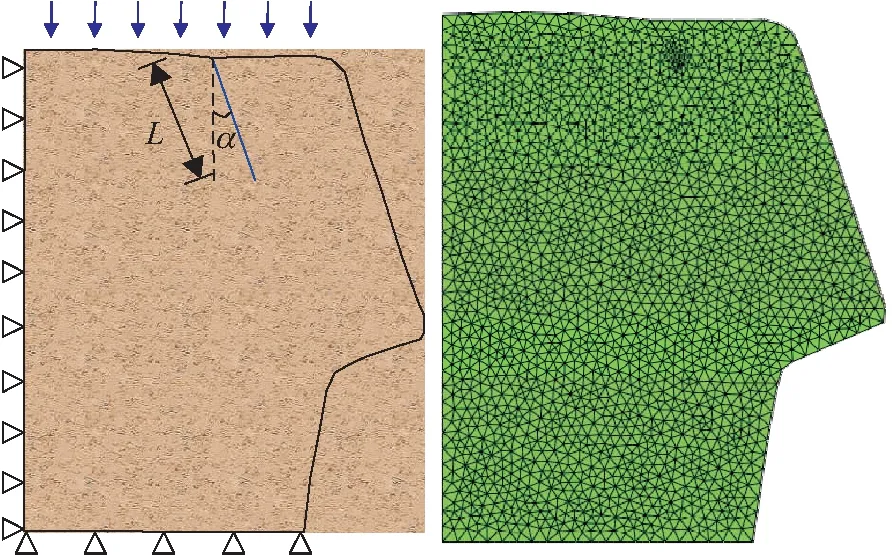
图3 危岩体示意图Fig.3 Schematic diagram of dangerous rock mass

2. 2 计算模型及模型概况

该危岩体的高度为20.5 m，长度为9.5 m，厚度为4 m，其中裂隙位于危岩体中部，裂隙长度为

L

(m)，裂纹方向与竖直方向的夹角为

α

(°)。危岩体由长石石英砂组成，其重度为24.8 kN/m，岩体的抗拉强度为480 kPa，岩体的弹性模量为8 000 kPa，其泊松比为0.25，岩体的Ⅰ型断裂韧度为1.796×10N/m。为了研究在不同裂隙倾角

α

、不同裂隙长度

L

以及不同降雨强度下危岩体的断裂力学特性，将裂隙倾角

α

分别取为0°、30°、60°，裂隙长度

L

分别取为2 m和4 m，降雨分为天然工况与暴雨工况，为了简化计算，根据文献[16]的研究结果，天然工况下裂隙内部水压力取为裂隙深度的1/3，而暴雨工况下裂隙内部水压力则取为裂隙深度的2/3。

2. 3 计算结果分析

2.3.1 不同工况下危岩体的应力及位移分析

对初始条件下的不同裂隙倾角、裂纹长度以及降雨工况下危岩体裂纹尖端的应力云图进行分析，如图4至图6所示，为了简化篇幅及便于阅读，图4给出了裂隙倾角α分别为0°、30°、60°，裂隙长度

L

为2 m，以及暴雨工况下危岩体的最大主应力、剪应力和水平位移云图；图5给出了裂隙倾角

α

为0°,裂隙长度

L

分别为2 m和4 m以及暴雨工况下危岩体的最大主应力、剪应力和水平位移云图；而图6则给出了裂隙倾角

α

为0°,裂隙长度

L

为2 m，以及天然工况与暴雨工况下危岩体的最大主应力、剪应力和竖向位移云图。由图4至图6可见，无论何种工况，危岩体的应力在裂纹尖端形成应力集中，同时其水平位移在裂纹处呈现不连续特征，且危岩体主控面的左侧水平位移较小(几乎为0)，而其右侧水平位移较大，表明在自重及裂隙内水压的作用下，危岩体主控面发生了张开效应；对于不同裂隙角度

α

而言，随着裂隙角度的增大，裂隙对危岩体变形的影响逐渐减小，由危岩体水平位移云图可见其水平位移主要集中于危岩体的突出部位；对于不同裂隙长度

L

而言，随着裂隙长度的增加，危岩体的应力集中程度越大，同时其最大水平位移主要发生在裂隙部位；而对于天然工况与暴雨工况而言，暴雨工况下应力集中程度更大，变形更剧烈。

对图4至图6中不同工况下危岩体的最大主应力、剪应力及水平位移进行统计，其结果列于表1。

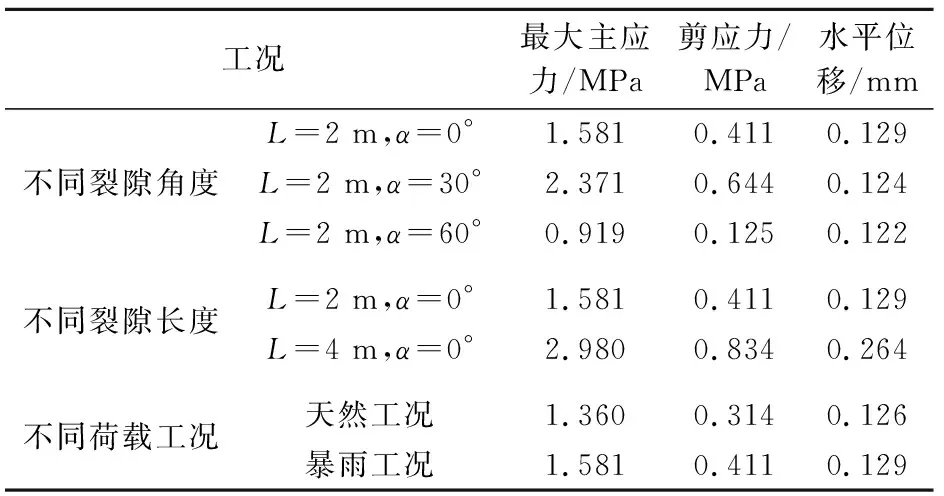
表1 不同工况下危岩体的应力及变形统计

由表1可知：对于不同裂隙角度而言，危岩体的最大主应力值和剪应力值随着裂隙角度的增大呈现先增后减的趋势，表明相同条件下在裂隙角度接近30°左右时危岩体的应力集中程度最大，而当裂隙角度进一步增大后危岩体的应力集中程度明显降低，但是其水平位移值随着裂隙倾角的增大呈现持续减小的趋势，表明裂隙倾角越小对危岩体整体稳定性的影响越大；对于不同裂隙长度而言，裂隙长度的增大对危岩体应力及变形的影响最大，本文

L

=4 m工况较之

L

=2 m工况危岩体的最大主应力值和剪应力值分别增长了88.49%和102.91%，而其水平位移值则增加了104.65%，可见裂隙长度的增大对危岩体稳定性的影响最大；对于不同荷载工况而言，暴雨工况增大了危岩体的应力集中及变形程度，较之天然工况，暴雨工况下危岩体的最大主应力和剪应力值增长了16.25%和30.89%，其水平位移值增加了2.38%，可见暴雨一定程度上增加了危岩体的失稳程度，但是其影响要小于危岩体的裂隙长度。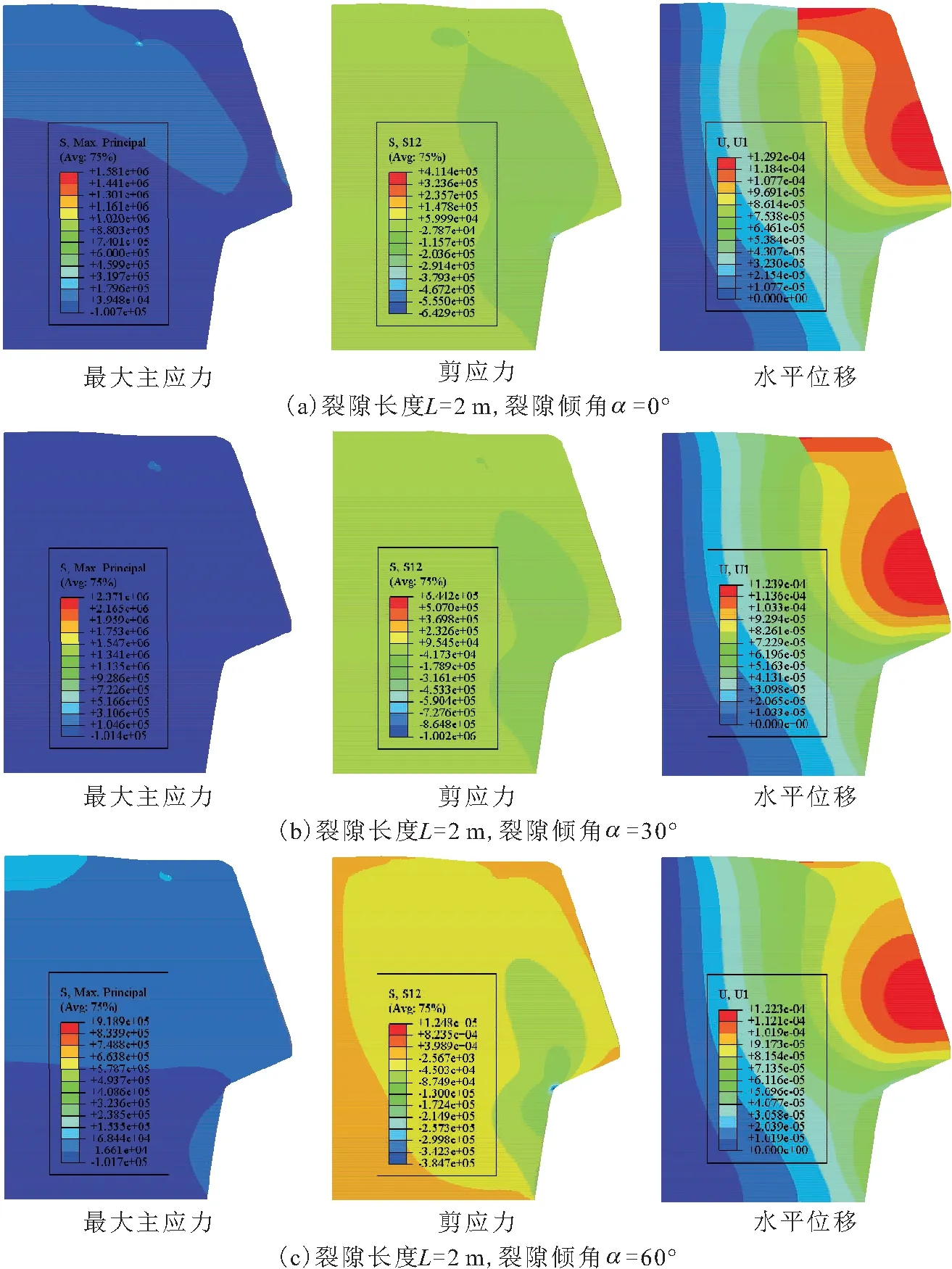

图4 不同裂隙倾角下危岩体的应力云图(单位：kPa)Fig.4 Stress cloud map of dangerous rock under different fracture dip angles(unit:kPa)

2.3.2 危岩体裂纹扩展过程分析

限于篇幅，本文即给出危岩体较为危险的工况：即不同裂隙长度(

L

=2 m和4 m)工况下危岩体裂隙扩展的全过程，见图7。

图5 不同裂隙长度下危岩体的应力云图(单位：kPa)Fig.5 Stress cloud map of dangerous rock under different fracture lengths(unit:kPa)

图6 天然工况与暴雨工况下危岩体的应力云图(单位：kPa)Fig.6 Stress cloud map of dangerous rock under natural and rainstorm conditions(unit:kPa)

由图7可见，危岩体的主控面(即图7中危岩体的裂隙)在自重及暴雨的作用下，逐渐向右下方扩展，且靠近危岩体的尖点处，裂隙长度越大，危岩体掉落块体的体积也越大。

图7 危岩体裂纹扩展的全过程Fig.7 Whole process of crack propagation in dangerous rock mass

为了探究危岩体裂纹扩展过程中裂纹尖端应力强度因子的变化规律，对图7中两种工况下危岩体裂纹尖端的应力强度因子随裂纹扩展长度的变化进行了追踪，其结果见图8。

图8 两种工况下危岩体裂纹尖端的应力强度因子 随裂纹扩展长度的变化曲线Fig.8 Variation curves of stress intensity factor at crack tip of dangerous rock mass with crack propagation length under two working conditions

由图8可见，随着裂纹长度的不断扩展，危岩体裂纹尖端的Ⅰ型应力强度因子和Ⅱ型应力强度因子的绝对值也在不断地增大，同时危岩体裂纹尖端的Ⅰ型应力强度因子与Ⅱ型应力强度因子在危岩体裂纹扩展初期的量级一致，但是随着危岩体裂纹长度不断扩展后，危岩体裂纹尖端的Ⅰ型应力强度因子的绝对值也不断增大，而其Ⅱ型应力强度因子的绝对值则变化不大，表明危岩体裂纹扩展过程中Ⅰ型扩展占主导地位，而值得注意的是，初始裂纹长度越长，危岩体裂纹尖端的Ⅰ型应力强度因子和Ⅱ型应力强度因子的绝对值越大，表明此时危岩体越容易失稳。

3 结 论

本文基于Abaqus软件平台，利用Python语言开发编制了基于断裂力学理论的危岩体裂纹任意扩展的网络重构数值模拟方法，并利用该方法对重庆市万州太白编号为W15的危岩体稳定性进行了数值仿真分析，得到了以下结论：

(1) 基于围道积分及断裂力学理论，对Abaqus软件进行了二次开发，利用Python语言实现了危岩体裂纹扩展、方向判断及应力强度因子计算的全过程，为危岩体断裂变形特性模拟提供了一种新的数值模拟方法。

(2) 危岩体的最大主应力值和剪应力值随着裂隙角度的增大呈现先增后减的趋势，危岩体的水平位移值随着裂隙倾角的增大持续减小；随着裂隙角度的增大，裂隙对危岩体变形的影响逐渐减小，其水平位移主要集中于危岩体的突出部位。

(3) 危岩体裂隙长度的增大对危岩体应力及变形的影响最大，使得变形由危岩体的突出部位向裂隙处集中；暴雨工况下危岩体的变形及位移较之天然工况要大，是影响危岩体稳定的重要因素之一。

(4) 危岩体裂纹朝着危岩体突出部位进行扩展，主要受到Ⅰ型扩展主导，随着裂纹的不断扩展，危岩体裂纹尖端的Ⅰ型应力强度因子呈现指数型上升，Ⅱ型应力强度因子变化不大，初始裂纹长度越长，危岩体裂纹尖端的Ⅰ型应力强度因子和Ⅱ型应力强度因子的绝对值越大。