基于云化物元耦合模型的岩质高边坡工程爆破施工安全风险评估

涂圣文，赵振华，邓梦雪，王 冰

(贵州师范大学材料与建筑工程学院，贵州 贵阳 550025)

公路桥梁、隧道和高边坡是公路工程施工中的三大高风险环节，往往生产安全事故多发。对于山区高速公路而言，岩质高边坡工程尤为常见。爆破施工作为岩质高边坡的主要开挖方式，施工期间产生的爆破振动对边坡坡体的稳定性以及临近重要构筑物的安全具有一定的影响，其安全风险评估已成为山区高速公路建设过程中亟需解决的重要问题之一。

为了完善高速公路路堑高边坡工程施工安全风险评估体系，加强路堑高边坡工程施工风险管理，我国交通运输部于2014 年12 月发布了《高速公路路堑高边坡工程施工安全风险评估指南(实行)》(以下简称《指南》)。《指南》将高速公路路堑高边坡工程施工安全风险评估分为总体风险评估和专项风险评估两个层面，并分别推荐了各层面采用的安全风险评估指标体系和评估方法。但总体而言，《指南》所推荐的路堑高边坡工程施工安全风险评估指标体系和评估方法较为宏观，缺乏针对岩质高边坡爆破施工这类专项工程的相关规定。

为了合理评估并有效控制岩质高边坡工程爆破施工安全风险，近年来不少研究机构和研究人员开展了一系列相关的研究工作。如陈江基于Abaqus 有限元软件，建立了隧道—边坡三维数值计算模型，研究了大断面公路隧道洞口段爆破开挖对边坡稳定性的影响特征；陶张志等结合实际工程项目，在保障施工安全、质量、效率和边坡美观的情况下，提出了一套行之有效的岩质高边坡工程爆破施工技术方案；黄梦昌等采用现场爆破振动监测和数值模拟的方法，研究了改扩建工程中爆破振动对既有边坡岩体损伤的影响机理；何忠明等综合考虑边坡高度、坡形坡率、地质条件、爆破设计方案、爆区环境以及安全监督与管理等因素，建立了基于集对可拓粗糙集方法的高边坡爆破施工安全风险评估模型。

总体上来看，现有的研究多是采用数值模拟方法来分析爆破施工对高边坡稳定性的影响。但由于岩质高边坡工程爆破施工安全风险的影响因素众多,不仅有地质方面的因素，而且还有设计方案和施工管理等方面的因素，其中许多因素很难量化并具有一定的随机性和模糊性，因此单一的数值模拟方法很难综合考虑这些因素。为了综合考虑岩质高边坡工程爆破施工安全风险评估问题的区间模糊性、随机性和离散性特征，本文借鉴云模型改进的物元评估模型，构建了岩质高边坡工程爆破施工安全风险评估不确定分析模型，使得评估结果更具有科学性、准确性和客观性。

1 岩质高边坡工程爆破施工安全风险评估指标体系

1. 1 安全风险评估指标体系构建

本文构建的岩质高边坡工程爆破施工安全风险评估指标体系中评估指标的选取参照《指南》中推荐的相关标准和有关文献，采用主成分分析法、专家咨询法等综合确定，最终确定的安全风险评估指标体系包括边坡规模、地质条件、设计因素和环境及管理因素四个方面共计6个评估指标，详见图1。

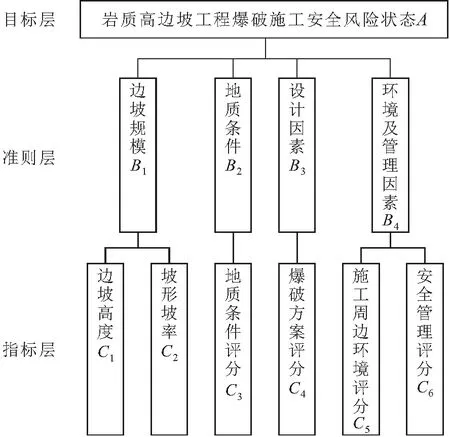
图1 岩质高边坡工程爆破施工安全风险评估指标体系Fig.1 Safety risk assessment index system for blasting construction of rock high slope engineering

1. 2 评估指标的分级和安全风险度量

要对高边坡工程爆破施工安全风险状态进行评估，首先必须对所选取的评估指标逐个进行安全状态评判。《指南》中将高速公路路堑高边坡工程施工总体风险和专项风险评估指标均划分为极高风险(Ⅳ)、高度风险(Ⅲ)、中度风险(Ⅱ)、低度风险(Ⅰ)4个安全风险等级，本文参照《指南》中的做法，将6个评估指标按低度风险、中度风险、高度风险和极高风险4个安全风险等级进行划分，其具体安全风险等级的划分标准主要参照《指南》的建议和相关文献。6个评估指标中，边坡高度

C

和坡形坡率

C

为量化评估指标，其中边坡高度是决定路堑边坡爆破施工难度的直接因素，边坡越高，爆破施工难度越大，其安全风险也越高；坡形坡率以路堑边坡超过所在自然斜坡比拟坡度值

Δα

来表示(参照《指南》中的建议)，

Δα

值越大，表明边坡越陡，爆破施工安全风险越高；地质条件

C

、爆破方案

C

、施工周边环境

C

和安全管理

C

为定性评估指标，其量值的确定由专家按百分制打分法综合确定。各评估指标具体等级划分标准见表1。

表1 岩质高边坡工程爆破施工安全风险评估指标风险等级划分标准

1. 3 评估指标权重的确定

《指南》中对各评估指标权重系数的确定推荐采用重要性排序法，但由于该方法本质上属于主观赋权法，其结果受人为因素的影响较大。为了减少评估指标权重确定的工作量，并增加评估指标权重系数的客观性，本文采用经变异系数改进的CRITIC法来确定评估指标C～C的权重系数，其主要步骤如下：

(1) 建立原始评估指标矩阵=(

x

)×(其中，

x

为第

i

个风险事件第

j

个评估指标的实测值或评分值；

m

为待评事件数目；

n

为评估指标数目，本文中

n

取6)。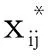

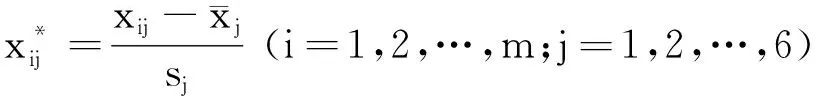
(1)

(3) 定义

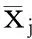
v

为各评估指标的变异系数，有：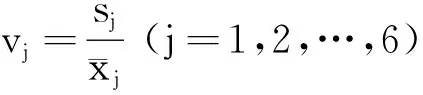

(2)

(4) 利用第(2)步得到的标准化矩阵，计算各评估指标之间的Pearson相关系数，并构造相关系数矩阵=(

r

)×(

k

=1,2,…,6;

j

=1,2,…,6)，再由矩阵，按下式计算各评估指标的独立性系数

η

：

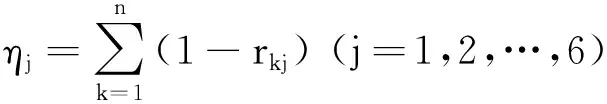
(3)

(5) 根据上述求得的各评估指标的变异系数和独立性系数，由下式计算各评估指标的重要性系数

C

：

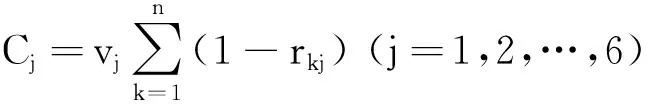
(4)

上式表明：

C

值越大，评估指标

j

在评估指标体系中越处于中心地位，其重要性越高，应赋予其较大的权重。因此，可由下式计算第

j

个评估指标的权重

w

：

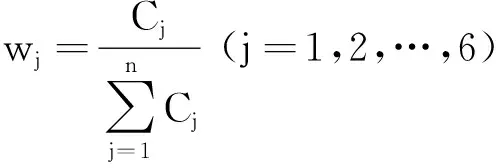
(5)

2 岩质高边坡工程爆破施工安全风险评估的云化物元耦合模型

如上文所述，高边坡工程爆破施工安全风险的影响因素较多，这些因素在一定区间内往往具有模糊性、随机性的分布特征，因此高边坡工程爆破施工安全风险评估属于复杂的不确定分析问题。文献[1]中采用了物元可拓方法来处理高边坡工程爆破施工安全风险评估问题，虽然物元理论通过关联函数对事物特征进行定量计算，能解决评价对象内容不相容的问题，但由于其是将特征量值通过具体数值区间来确定，因而忽略了量值的随机性和模糊性。而由李德毅院士在20世纪90年代提出的用来实现定性概念与定量数值之间双向转换的云模型，则能有效克服以上缺陷。因此，采用云模型对传统的物元理论进行改进，构建云化物元耦合模型，能够发挥物元理论和云模型的组合优势，更加科学、全面地处理复杂不确定分析问题中的随机性和模糊性，已经在各类风险评估问题中得到了一定的应用。

2. 1 云化物元模型的基本形式

物元理论一般以事件名称

M

、事件属性特征

F

和事件属性特征量值三者为集合来描述待分析的事件，以物元作为描述事件的基本元，形成一个有序三元组，记为=(

M

，

F

，

V

)，用矩阵可表示如下：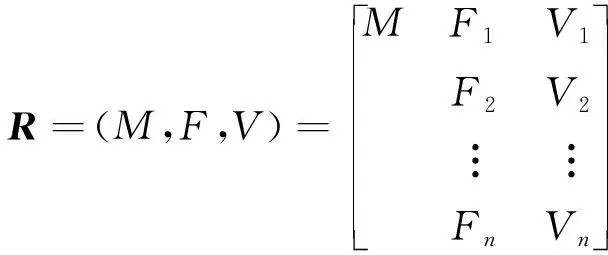

(6)

传统的物元模型中，=(

M

，

F

，

V

)中的事件属性特征量值通常被看作是确定的数值，而现实风险评估事件中诸多属性值则具有明显的随机性和模糊性，若用云模型的数字特征值(

E

,

E

,

H

)代替特征量值

V

，则可构建云化物元模型如下：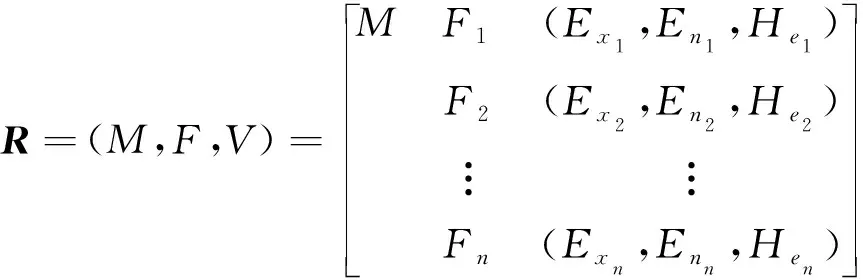

(7)

式中:

E

为期望，代表着云重心的位置；

E

为熵，表示云代表的定性概念的模糊程度；

H

为超熵，主要体现样本的随机性，即云图上云滴的厚度。云模型用这三个数字特征反映定性概念整体的定量特征。

2. 2 云模型参数的计算

云化物元模型中，在对岩质高边坡工程爆破施工安全风险等级区间进行划分时，利用云模型的模糊性和随机性，将传统物元模型的区间边界值模糊化，即将评估指标的分类等级界限作为一个双约束空间[

C

，

C

]处理，根据下面正态云模型的转换公式，可求出岩质高边坡工程爆破施工安全风险各评估指标分类等级界限云模型的期望

E

、熵

E

和超熵

H

:

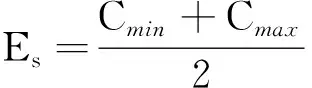
(8)

(9)

H

=

s

(10)

式中：

C

、

C

分别为评估指标分类等级区间的最小值和最大值；

s

为常数，可结合岩质高边坡工程爆破施工安全风险评估指标的模糊性、随机性和实际情况进行调整。将表1中的各评估指标分类等级区间量值代入公式(8)～(10)，可计算得到各评估指标的标准正态云模型的期望

E

、熵

E

和超熵

H

，其计算结果见表2。在云模型参数的计算中，根据相关研究，

s

值按

s

=0.1

E

选取。

表2 岩质高边坡工程爆破施工安全风险各评估指标分类等级界限云模型参数值

根据云模型生成算法，结合表2中岩质高边坡工程爆破施工安全风险各评估指标的云模型参数值，通过Matlab模拟计算出各评估指标的评估云图，由于篇幅所限，这里仅给出边坡高度评估指标

C

的评估云图，如图2所示。

图2 边坡高度C1评估云图Fig.2 Assessment cloud map for slope height C1

2.3 评估指标云关联度计算

云模型与物元理论耦合后，传统物元分析方法中的隶属度函数就不再适用，需要根据云模型的相关算法来计算评估指标的云关联度。

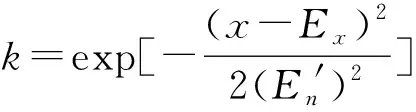
(11)

根据公式(11)，逐一计算出待评估指标与安全风险等级标准正态云之间的云关联度，可组成云关联度矩阵：

(12)

式中:

k

为评估指标

C

与安全风险等级

l

之间的云关联度；

n

为评估指标数目，本文为6；

l

为安全风险等级序号，本文为1～4的整数。

2. 4 安全风险等级确定

首先，用评估指标权重向量与云关联度矩阵相乘，得到综合评估向量：=·

(13)

式中：评估指标权重向量由各评估指标C～C的权重

w

(

j

=1,2,…,6)组成，

w

由上文所述方法确定。对综合评估向量中的诸元素

b

，应用加权平均法求得评估事件的综合评估分数

r

:

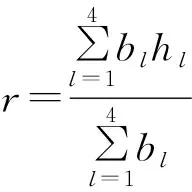
(14)

式中:

h

为安全风险等级

l

的赋分值，本文对安全风险等级Ⅰ～Ⅳ分别赋予1、2、3、4分。由公式(14)计算得到的综合评估分数

r

接近于哪个数值，安全风险等级就评判为与该数值对应的等级。

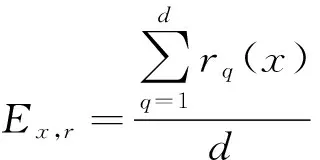
(15)

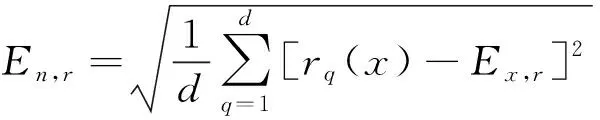
(16)

式中：

r

(

x

)为第

q

次计算得到的综合评估分数。由于均值

E

,能反映岩质高边坡工程爆破施工安全风险等级的评估分数，而标准差

E

,则表达的是评估结果的离散性，其值越大，评估结果越分散。因此，定义置信度因子

β

为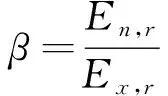

(17)

上式表明：

β

值越小，评估结果的分散性越小，评估结果越可靠。一般情况下，若

β

<0.05时可认为评估结果可信。

3 实例应用与分析

本文以西南某山区高速公路项目8处岩质高边坡工程爆破施工安全风险评估为例，阐述本文方法的应用步骤和应用效果。

首先，根据该项目爆破方案，统计得到该8处岩质高边坡工程的边坡高度和坡形坡率参数;再选取5位工程建设、安全管理及爆破工程等领域的专家，由专家根据实际情况对每处工程的地质条件、爆破方案、施工周边环境和安全管理4个评估指标在0～100分之间进行打分后取平均值，整理后得到该高速公路项目岩质高边坡工程爆破施工安全风险各评估指标的原始评分值，见表3。

表3 某高速公路项目岩质高边坡工程爆破施工安全风险各评估指标的实测值或评分值

然后，采用基于改进的CRITIC法确定各评估指标的权重。根据公式(1)～(5)求得边坡高度

C

、坡形坡率

C

、地质条件

C

、爆破方案

C

、施工周边环境

C

和安全管理

C

各评估指标的权重为=[

w

,

w

,…,

w

]=[0.119,0.192,0.161,0.164,0.211,0.154]。最后，根据第2.2～2.4节所述的评估方法，编制安全风险评估的Matlab程序，分别计算上述8处岩质高边坡工程爆破施工的安全风险等级。该程序的主要计算步骤如下：①根据表2中各评估指标分类等级界限云模型的3个数字特征，让每个安全风险等级对应一朵云，利用正态云发生器生成4朵正态云，其中边坡高度

C

的4朵正态云见图2；②针对每个评估案例，分别输入表3中6个评估指标的实测值或评分值，根据公式(11)计算求得各评估指标与安全风险等级标准正态云之间的云关联度；③按第1.3节方法求得各评估指标的权重值，根据公式(13)求得各案例的综合评估向量，并根据公式(14)求得各案例的综合评估分数；④为了减少随机因素的影响，按上述步骤重复计算100次，根据公式(15)和(16)计算得到综合评估分数的均值和标准差，并根据公式(17)求得置信度因子，以判断评估结果的可信度，具体计算结果见表4。此外，为了检验本文所述方法的有效性，采用传统物元法、云模型法、集对分析法3种常用方法对上述8处岩质高边坡工程爆破施工的安全风险等级进行了评估，具体评估结果见表4。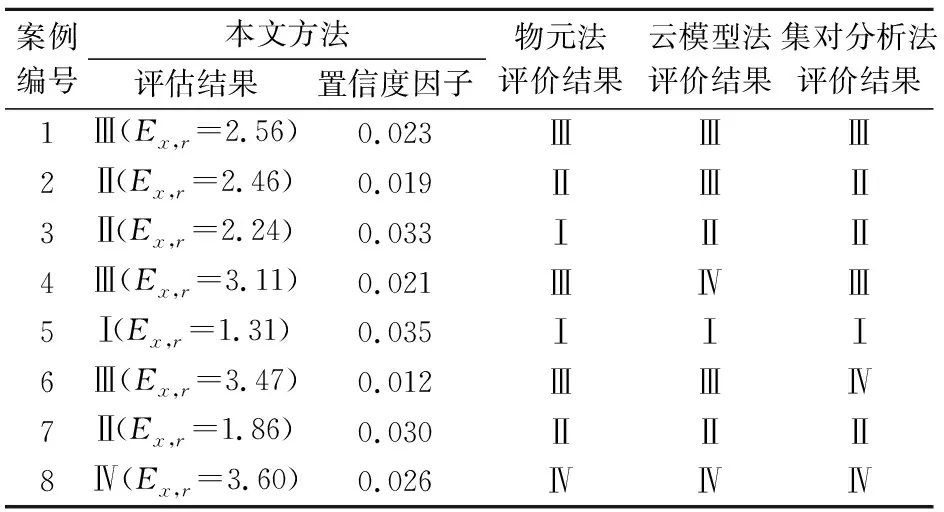

表4 8处岩质高边坡工程爆破施工安全风险评估结果

由表4可知，本文方法的评估结果与传统物元法、云模型法、集对分析法3种常用方法的评估结果基本吻合，且各评估案例的置信度因子均小于0.05，表明本文提出的云化物元耦合模型方法应用于岩质高边坡工程爆破施工安全风险评估是合理、有效的。

将本文云化物元耦合模型方法与传统物元法、云模型法、集对分析法单独进行了比较，其评估结果均具有较高的相似性。其中，本文方法与传统物元法和集对分析法相比，有87.5%的评估结果是相同的；本文方法与云模型法相比，有75%的评估结果是相同的。同时，根据表4中4种方法评估结果的统计分析可知，案例1、案例4、案例6评估结果为Ⅲ级的最多，案例2、案例3、案例7评估结果为Ⅱ级的最多，案例5评估结果为Ⅰ级的最多，案例8评估结果为Ⅳ级的最多。由此可以看出，各案例评估结果最多的安全风险等级与云化物元耦合模型方法的评估结果完全相同，说明本文云化物元耦合模型方法较其他评估方法的评估结果更具有代表性。

此外，本文云化物元耦合模型方法通过采用综合评估分数均值

E

,来界定安全风险等级，相较于其他评估方法，能够提供评估案例更多的综合信息。例如案例1和案例4，采用云化物元耦合模型方法对其进行安全风险评估时其评估结果均为Ⅲ级，但案例4的综合评估分数均值3.11高于案例1的综合评估分数均值2.56，表明案例4的爆破施工危险性要高于案例1。分析表3中案例4和案例1的原始评分值可以看出，案例4和案例1的6项评估指标的相对风险程度各有高低。其中案例4的边坡高度、坡形坡率、地质条件3个评估指标的风险程度要高于案例1，而案例1的爆破方案、施工周边环境、安全管理3个评估指标的风险程度要高于案例4。由于云化物元耦合模型方法一方面保留了传统物元理论善于解决评估指标间不相容问题的优点，另一方面由于云模型的引入，可将岩质高边坡工程爆破施工安全风险评估过程中的模糊性和随机性实现量化转换，从而准确地反映爆破施工安全风险评估的不确定性特点。因此，采用本文的云化物元耦合模型方法对岩质高边坡工程爆破施工安全风险等级进行评估，比其他评估方法更加全面，且评估结果具有更高的可靠性。

4 结论与建议

为了有效解决岩质高边坡工程爆破施工安全风险评估这个复杂的不确定性问题，本文首先采用经云模型改进的云化物元耦合模型，充分发挥了物元理论和云模型的组合优势来处理岩质高边坡爆破施工安全风险评估中普遍存在的模糊性、随机性和离散性特征；然后采用基于改进CRITIC的客观赋权法，基于评估指标实测数据和评分数据，通过挖掘评估指标的信息量和评估指标之间的相关性来确定评估指标的权重，使得评估结果更具有可信性；最后以某高速公路项目8处岩质高边坡工程爆破施工安全风险评估为案例，阐述了本文方法的应用步骤，并将本文方法的评估结果与传统物元法、云模型法、集对分析法3种常用方法的评估结果进行了对比分析，以检验本文方法的应用效果。结果表明：本文云化物元耦合模型方法的评估结果与3种常用方法的评估结果基本吻合，且各评估案例的置信度因子均小于0.05，说明本文提出的云化物元耦合模型方法应用于岩质高边坡工程爆破施工安全风险评估是合理、有效的;该云化物元耦合模型方法通过采用综合评估分数均值来判定安全风险等级，相较于其他评估方法，能够提供评估案例更多的综合信息，且比其他评估方法能够更加全面地反映评估指标间包含的不确定关系，使得评估结果具有更高的可靠性。

需要指出的是，岩质高边坡工程爆破施工安全风险评估中，各评估指标安全风险等级的划分标准和评估指标的评分取值是否合理也会对评估结果产生较大的影响。因此，在后续的研究中，还需进一步补充和完善岩质高边坡工程爆破施工安全风险评估指标体系，并研究评估指标评分取值及其安全风险等级划分标准等问题，以进一步提高评估指标体系的科学性，增强评估结果的全面性和客观性。