综采工作面过空巷围岩稳定性的影响因素研究
王 宏,王建彬,赵 斌
(山西晋煤集团技术研究院有限责任公司,山西 晋城 048006)
在整合复采和设计短视的影响下,综采工作面过平行空巷成为矿井复杂条件开采中的常见难题之一。工作面在过空巷的过程中,由于受釆动支承压力作用、巷道围岩弱化、维护时间较长等多方面不利因素,空巷的顶板容易下沉、两帮易片帮,甚至可能引起上覆岩层的移动或失稳。当综采工作面与空巷贯通后,容易发生大面积的顶板垮落,甚至压死液压支架,严重影响煤矿安全生产[1]。
针对此问题,郑志军[2]建立了工作面过空巷的顶板力学模型,分析了工作面过空巷时上方基本顶的破断位置;孙晓明等[3]基于岩层运动中心建立的矿山压力理论为指导思想,以切顶短臂梁为理论基础,提出了综放工作面过空巷切顶卸压结合恒阻大变形锚索支护技术;郑文翔[4]在分析工作面顶板物理模型的基础上建立稳定性力学模型,分析顶板稳定性和煤柱稳定性的关系;徐青云等[5]揭示了空巷顶板稳定机理,确定顶板破断产生滑落失稳是造成压架的主要原因,进而确定维持空巷顶板稳定的最小支护阻力;何向宁等[6]用FLAC3D软件对比分析了工作面回采过程中,在木垛支护、锚杆支护和高水充填 3 种支护方式下空巷围岩的稳定性。
前人虽然做了大量的研究工作,但对不同因素下工作面过空巷时围岩稳定性的变化规律研究较少。因此,采用ANSYS软件建立数值模型,分析埋深、采高、空巷宽度这三个因素发生变化时对工作面过空巷围岩稳定性的影响,给相关的设计和施工提供参考。
1 工作面过空巷围岩稳定影响因素分析
空巷的围岩失稳破坏主要表现为顶板下沉、两帮片帮和煤柱破坏,采煤工作面与空巷贯通后易引起大面积的顶板垮落,因此空巷顶板管理显得尤为重要,需要重点分析空巷顶板破坏机理。
如图1、图2所示,将空巷顶板简化为受均布载荷q、两边固支的无限长梁进行分析。

图1 空巷顶板简化力学模型Fig.1 Simplified mechanical model of abandoned roadway roof
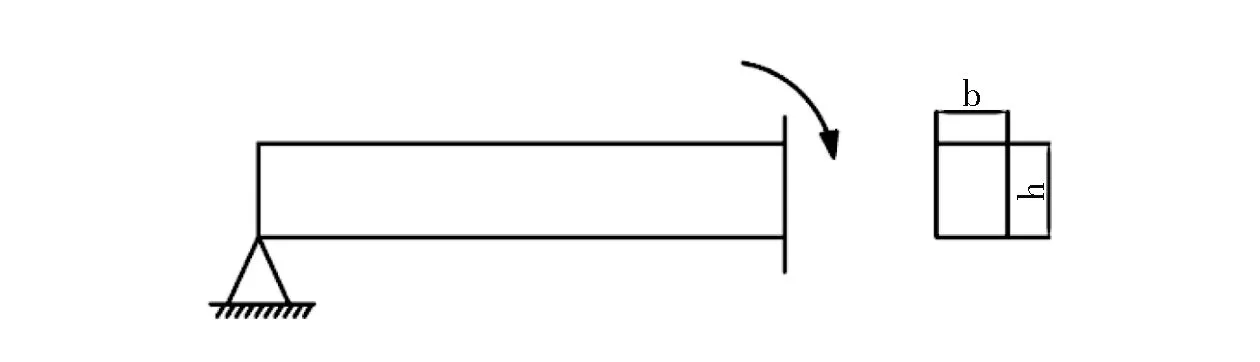
图2 空巷顶板组合梁弯曲截面Fig.2 Bending section of composite beam of abandoned roadway roof
对上述力学模型进行受力分析,根据梁的对称性,可取梁的一半长度进行分析。由平衡原理,可得空巷顶板的挠度方程为
(1)
E1I1ym=q1-ky(0≤x≤∞) .
(2)
解方程(1)可得:
解方程(2)可得:
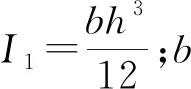
分析可知,空巷顶板破坏的主要影响因素有空巷宽度、空巷埋深、围岩性质、岩体完整性、空巷围岩地应力等[7]。另外,现场开采实践证明,采高增加带来的工作面矿压显现给工作面安全生产带来重要影响,采高越大,工作面顶板压力随之增大,煤壁前方支承应力集中程度也增大,形成的支承压力峰值区距离工作面煤壁越远,加剧了工作面煤壁片帮和冒顶,对工作面前方空巷的应力分布产生影响[8]。因此,选取埋深、工作面采高、空巷宽度作为主要影响因素分析采煤工作面过空巷时的围岩稳定性。
2 数值模型
2.1 数值模型的建立
依据晋煤集团长平矿的实际地质条件,建立综采工作面与空巷的ANSYS三维数值模型。为了简化计算,做出以下假设:
1)假定煤岩体是理想弹塑性体,不考虑煤岩体内的各种结构面。
2)假定初始应力场为自重应力场。
3)假定围岩中无地下水,不考虑地下水对有效应力的衰减作用[9]。
根据试算,排除边界影响,该模型计算尺寸为1 000 m(长)×300 m(宽)×300 m(高)。采煤工作面倾向长度200 m,走向长度800 m,采高依据不同模拟情况进行调整。由于采场各层岩性的不同,模型从上到下共划分为5层,模拟计算中采用的各岩层计算参数见表1。
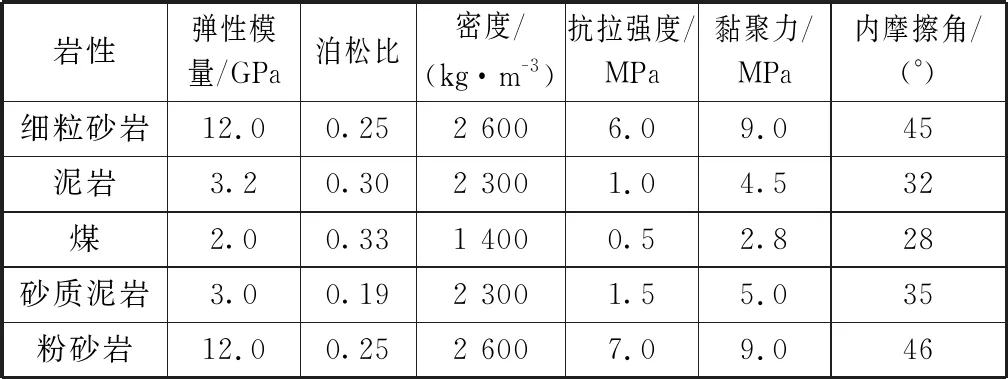
表1 煤岩体的力学参数Table 1 Mechanical parameters of coal and rock mass
模型底部施加竖直方向位移约束,模型前后左右四个面上均施加水平方向位移约束,上边界以上岩体质量折算成均布荷载后施加于模型上表面,计算考虑重力作用,施加重力载荷。计算分两步进行,第一步模拟重力场,第二步模拟工作面的回采。
2.2 计算参数的选取
依据长平矿煤岩体力学参数,工作面顶板以上岩层的平均重度近似取值2 000 kg·m-3,根据晋城矿区部分煤矿的实际情况,数值模型中综采工作面埋深选取100 m、250 m、400 m,可计算出不同埋深对应模型顶部载荷分别为2 MPa、5 MPa、8 MPa,综采工作面的采高分别选为2 m、4 m、6 m,空巷的宽度分别选为3 m、5 m、7 m。
3 不同因素对综采工作面过空巷影响分析
空巷的围岩失稳破坏主要表现为顶板下沉、两帮片帮和煤柱破坏,因此重点分析在不同影响因素下,空巷顶板沉降值、煤壁位移值和煤柱切向应力值的变化情况。
3.1 不同埋深下空巷围岩稳定性分析
数值模型中综采工作面埋深选取100 m、250 m、400 m,换算成模型顶部载荷分别为2 MPa、5 MPa、8 MPa,模拟计算结果如图3、图4所示:
由图3可知,综采工作面过空巷时,随着埋深的增加,空巷顶板沉降值和煤壁位移值不断增加,近似呈正比关系。当工作面与空巷距离小于25 m后,随着工作面的继续推进,空巷顶板沉降值和煤壁位移值显著增加,位移曲线斜率明显增大,空巷稳定性越来越差。图4为综采工作面与空巷距离为10 m时的模型剖面图,通过对比不同埋深下的煤柱切向应力,可知不同埋深下的煤柱切向应力分布规律基本相同;但随着埋深增加,最大切向应力值由5.54 MPa逐渐增大到20.19 MPa,煤柱内应力值增高明显,稳定性变差。由此可知,埋深变化会对空巷的稳定性产生较大影响,埋深越大,空巷围岩变形越大、煤柱内应力越高、巷道稳定性越差、工作面过空巷时危险性越大。
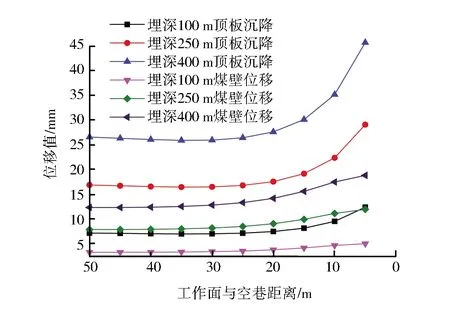
图3 不同埋深下空巷顶板和煤壁位移值Fig.3 Displacement of roof and coal wall of abandoned roadway under different buried depths

(a)埋深100 m

(b)埋深250 m

(c)埋深400 m图4 不同埋深下空巷煤柱切向应力剖面图Fig.4 Section of tangential stress of coal pillar in abandoned roadway with different buried depths
3.2 不同采高下空巷围岩稳定性分析
分别选取采高为2 m、4 m、6 m,建立数值模型分析采高变化对工作面过空巷时围岩稳定性的影响规律,模拟计算结果如图5、图6所示。

图5 不同采高下空巷顶板和煤壁位移值Fig.5 Displacement of roof and coal wall of abandoned roadway under different mining heights
由图5可知,综采工作面过空巷时,随着采高变大,空巷顶板沉降值和煤壁位移值略有增加,变化不大,位移曲线近似重合。当工作面与空巷距离小于25 m后,随着工作面继续推进,位移曲线斜率明显增大,空巷顶板沉降值和煤壁位移值显著增加,空巷稳定性越来越差。

(a)采高2 m
(b)采高4 m

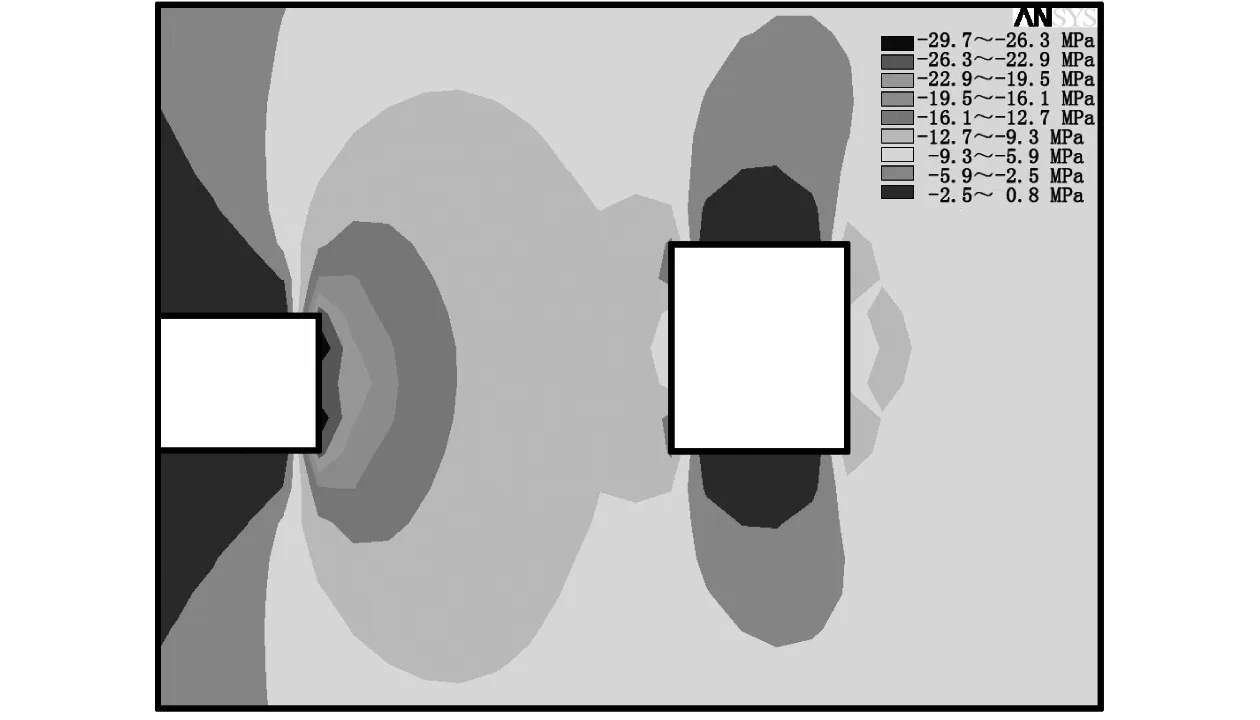
(c)采高6 m图6 不同采高下空巷煤柱切向应力剖面图Fig.6 Section of tangential stress of coal pillar in abandoned roadway with different mining heights
由图6的煤柱切向应力剖面图可知,采高不同,煤柱内部切向应力分布规律不同,随着采高逐渐增加,煤柱内部应力集中范围逐渐变大,但应力集中系数变小,煤柱由局部高应力变为整体大范围承载受力,扩大了煤柱受力面积但转移了局部的高应力。由此可知,采高变大对空巷围岩的位移变形影响较小,对煤柱的应力分布影响较大,采高增加使煤柱承载受力面积增加,但应力集中系数变小。
3.3 不同空巷宽度下空巷围岩稳定性分析
分别选取空巷宽度为3 m、5 m、7 m,建立数值模型分析空巷宽度变化对工作面过空巷时围岩稳定性的影响规律,模拟计算结果如图7、图8所示。
由图7 可知,综采工作面过空巷时,随着空巷宽度增加,空巷顶板沉降值显著增加,而空巷煤壁位移值变化不大。同样,当工作面与空巷距离小于25 m后,随着工作面继续推进,位移曲线斜率明显增大,空巷稳定性越来越差。由图8煤柱切向应力剖面图可知,随着空巷宽度增加,煤柱内部切向应力集中范围逐渐扩大贯通,且最大切向应力值逐渐增加,由12.18 MPa增加至13.57 MPa,煤柱的稳定性逐渐变差。由此可知,空巷宽度增加会显著破坏空巷顶板稳定性,同时会增大煤柱应力,对煤壁位移影响较小。

图7 不同空巷宽度下空巷顶板和煤壁位移值Fig.7 Displacement values of roof and coal wall under different abandoned roadway widths

(a)空巷宽3 m
(b)空巷宽5 m

(c)空巷宽7 m图8 不同空巷宽度下空巷煤柱切向应力剖面图Fig.8 Section of tangential stress of coal pillar with different abandoned roadway widths
4 结论
1)随着埋深的增加,空巷顶板沉降值、煤壁位移值、煤柱切向应力值都逐渐增加,空巷稳定性变差。
2)采高增大对空巷顶板沉降值和煤壁位移值影响较小,但会改变煤柱切向应力分布,使煤柱承载受力面积增大,应力集中系数变小。
3)空巷宽度增加会显著破坏空巷顶板稳定性,同时会增大煤柱应力,对煤壁位移影响较小。
4)综合不同影响因素分析可知,当工作面与空巷距离小于25 m后,随着工作面继续推进,空巷顶板沉降值和煤壁位移值显著增加,位移曲线斜率明显增大,空巷稳定性显著变差,此时应增强巷道和工作面的矿压监测、加强支护,防止空巷煤柱破坏和顶板突然垮落。

