基于小波去噪和神经网络的建筑工程沉降变形预测模型
陈 程
(内蒙古师范大学 纪委、监察专员办公室,内蒙古 呼和浩特 010022)
在高层建筑工程的施工过程中,沉降变形是描述建筑质量和安全、稳定的重要指标[1]。建筑工程沉降变形与多种因素相关,具有时变性。为了保证建筑工程的质量,需要对建筑工程沉降变形进行预测,并根据预测结果对工程质量进行有效管理。因此,建立高精度的建筑工程沉降变形预测模型具有重要意义[2-3]。
传统建筑工程沉降变形的预测模型有两种: 一种是根据建筑物的一些参数设计相应的模型,然后对建筑工程沉降变形过程进行模拟,找出该建筑工程沉降变形的变化特点,对将来一段时间的建筑工程沉降变形进行估计[4]。这类模型在建模过程中,对参数如何确定没有统一标准,而且当参数较多时,模型建立过程十分复杂,因此建筑工程沉降变形预测结果不稳定; 另一种是基于时间序列理论的建筑工程沉降变形预测模型,如线性回归等[5],这类模型不需建筑工程沉降变形的相关参数,直接根据建筑工程沉降变形的时间序列数据进行建模,建模过程简单,建筑工程沉降变形预测结果较好[6]。然而,建筑工程沉降变形过程是一个非线性动态系统,线性回归等模型无法揭示建筑工程沉降变形的非线性动态特征。为了解决线性回归等模型的缺陷,有学者引入人工智能方法中的支持向量机和神经网络[7-8],对建筑工程沉降变形进行预测,获得了比线性回归模型更优的建筑工程沉降变形预测结果。由于建筑工程沉降变形的数据中隐藏着一定的混沌性,而人工智能方法没有考虑这种混沌性,因此预测效果有待进一步改善。另外,建筑工程沉降变形的数据具有多种特征,而且数据中存在一定的噪声,因此建筑工程沉降变形的建模过程应考虑这些特征,以便获得理想的建筑工程沉降变形预测结果[9]。
小波分析是一种可以对数据进行多尺度分解的工具[10],重构时能够消除数据中的噪声,可以应用于建筑工程沉降变形的数据预处理。为了改善建筑工程沉降变形的预测效果,本文提出一种基于小波去噪和神经网络的建筑工程沉降变形预测模型,并通过建筑工程沉降变形预测实验对其性能进行了测试。
1 小波去噪和神经网络
1.1 小波去噪

(1)

(2)
其中a和b表示伸缩和平移因子。
设收集的建筑工程沉降变形的数据为
s(t)=x(t)+n(t),
(3)
其中n(t)表示噪声信号。为了消除s(t)中的噪声,得到真实信号x(t),采用小波分析对s(t)的离散信号s(n) (n= 0,1,2,L,…,N-1)进行变换,得到
(4)
其中W2js(k)表示小波系数。
在实际应用中,ψ(t)一般无显式表达,为此进行如下递归,

(5)
其中:h和g表示φ(t)和ψ(t)的低通和高通滤波器;xf(0,k)表示真实信号x(t);xf(j,k)表示尺度系数;Wf(j,k)表示小波系数。
采用重构低通和高通滤波器h0和g0,得到小波分析的重构形为
xf(j-1,k)=xf(j,k)×h0(j,k)+Wf(j,k)×g0(j,k),
(6)
可以消除建筑工程沉降变形数据中的噪声。
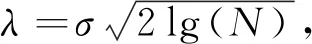
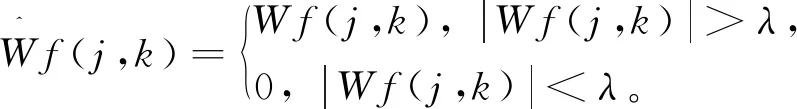
(7)
1.2 神经网络
神经网络有较强的非线性预测能力,其中BP神经网络是应用较为广泛的一种神经网络。本文选择BP神经网络对建筑工程沉降变形进行建模与预测。
设BP神经网络的输入层、隐含层、输出层的向量分别为
x=(x1,x2,…,xi,…,xn)T,
m=(m1,m2,…,mk,…,ml)T,
c=(c1,c2,…,cj,…,cm)T。
设输入层和隐含层的权值矩阵为v=(v1,v2,…,vk,…,vl)T,隐含层和输出层的权值矩阵为w=(w1,w2,…,wj,…,wm)T,则神经网络各层信号之间的数学关系可以描述如下,
输出层:
cj=f(netj),j=1,2,3,…,m,
(8)
(9)
隐含层:
mk=f(netk),k=1,2,3,…,l,
(10)
(11)
选择Sigmoid函数作为映射函数,定义为
(12)
1.3 预测步骤
(1) 收集建筑工程沉降变形相关数据。
(2) 采用小波分析对建筑工程沉降变形数据进行去噪处理。
(3) 采用混沌理论对去噪后的建筑工程沉降变形进行相空间重构,得到神经网络的学习样本。
(4) 采用BP神经网络建立建筑工程沉降变形预测模型。
2 建筑工程沉降变形预测应用实例
2.1 数据源
选择某工程建筑物的沉降观测点作为测试对象,收集到100个观测数据,其中前50个观测数据作为训练样本,其余的50个观测数据作为验证样本。采用小波分析对原始100个观测数据进行去噪处理。结果表明,小波分析能有效地消除原始数据中的噪声,有利于建筑工程沉降变形建模。
2.2 数据的混沌分析与处理
对去噪后的建筑工程沉降变形进行归一化操作,消除数据变化范围大给BP神经网络训练过程带来的不利影响,改善BP神经网络学习过程的收敛速度,具体为
(13)
归一化后的建筑工程沉降变形数据受到多种因素的影响,具有一定的混沌性,因此需要确定其延迟时间和嵌入维数,采用C-C法和Cao法分别确定建筑工程沉降变形序列的延迟时间和嵌入维数,结果如图1所示。由图1可知,最优延迟时间为6 s,最优嵌入维数为9。通过延迟时间和嵌入维数可以找到建筑工程沉降变形轨迹,更好地建立建筑工程沉降变形预测模型。

图1 建筑工程沉降变形序列的混沌分析Fig.1 Chaos analysis of sequence for building project settlement deformation
2.3 预测结果及分析
小波去噪和神经网络的建筑工程沉降变形模型的单步和多步预测结果如图2所示。对建筑工程沉降变形预测结果进行分析可以发现,单步建筑工程沉降变形预测结果明显优于多步建筑工程沉降变形预测结果,但它们的预测精度均可以满足建筑工程沉降变形建模的实际应用要求。实验结果表明,通过小波去噪可以有效地消除噪声对建筑工程沉降变形预测结果的不利影响,同时通过混沌分析可以进一步挖掘建筑工程沉降变形的变化特点,最后通过BP神经网络对建筑工程沉降变形的非线性进行预测,获得了理想的建筑工程沉降变形预测结果。

图2 建筑工程沉降变形预测的单步和多步结果Fig.2 Single step and multi-step prediction results of building project settlement deformation

表1 与其他模型的建筑工程沉降变形预测精度对比
为了测试本文模型的优越性,选择没有小波去噪的BP神经网络(BPNN)、线性回归模型(LR)、文献 [2] 和文献 [6] 的预测模型进行对比测试,统计它们对建筑工程沉降变形的预测精度,结果见表1。由表1可知,相对于对比的建筑工程沉降变形预测模型,本文模型的建筑工程沉降变形预测精度得到相应的提高,克服了对比模型存在的局限性,获得了更优的建筑工程沉降变形预测结果。
3 结语
建筑工程沉降变形具有混沌变化特性,且存一定的噪声干扰,使得传统模型难以获得高精度的预测结果。为了更好地预测建筑工程沉降变形,引入小波分析解决噪声的不利影响,加快BP神经网络的学习速度; 引入混沌理论分析建筑工程沉降变形的变化趋势,提取建筑工程沉降变形的原始演化信息; 通过BP神经网络学习建立非线性的建筑工程沉降变形预测模型。实验结果表明,本文的建筑工程沉降变形预测模型获得了比其他模型更高的建筑工程沉降变形预测精度,为复杂的建筑工程沉降变形预测提供了一种新的研究思路。

