机组非停扰动下PSS调节性能评估及参数校核

孟凡超,胡文平,刘翔宇

(国网河北省电力有限公司电力科学研究院,河北 石家庄 050021)

0 引言

随着远距离大容量输电系统的不断发展,电力系统稳定问题日趋复杂。暂态稳定呈现出了新的特点,动态稳定、电压稳定问题均日益严重,特别是以低频振荡为代表的小干扰稳定问题,对电网稳定的影响越来越突出[1-3]。

在低频功率振荡的抑制措施中,电力系统稳定器(PSS)具有概念清晰、结构简单、效果良好等优点,在国内外得到了广泛应用。作为同步发电机的一种附加励磁控制,PSS主要是通过在励磁电压调节器中引入领先于轴角速度的附加信号,增加系统的正阻尼转矩来实现对低频振荡的抑制。目前为止,PSS仍然是阻尼局部功率振荡最经济有效的措施。深入研究低频振荡的产生机理,结合工程现场实际系统地研究PSS参数对低频振荡抑制效果的影响以及PSS参数的优化整定方法,具有重要的学术价值和实际工程意义[4]。

至今,无论是在理论还是实践中,PSS参数整定已有众多的方法和技术。这些方法总体上分为两大类[5],一类是现场试验法,即在机组运行中,通过测试机组及其励磁系统的开环响应特性,进而设定PSS控制参数;另一类是模型分析法,即通过机组和电网的数学模型,通过理论推导或时域仿真来设计和校验PSS参数。现场测试法的局限在于只能在机网少数运行方式和振荡模式情况下整定和验证PSS控制参数;模型分析法的缺陷在于模型的准确性存疑。

考虑到实际电网的不断演变以及运行方式多变性,PSS实际控制效果如何,就成为十分重要的问题。但长期以来,缺乏一套对PSS 抑制低频振荡的实效进行在线评估的手段[6]。火电机组是一个包括锅炉、汽轮机、发电机的复杂发电系统,由于锅炉泄漏、汽轮机振动、热工保护动作、厂用电系统故障等原因引起的机组非计划停运(简称“非停”)时有发生。基于WAMS系统数据,利用非停机组对在运机组的大扰动,提出一种在线评估PSS调节性能的方法[7]。

1 PSS性能评估方法的相移原理

PSS性能评估的基本原理见图1。

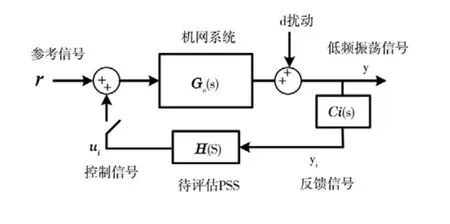
图1 PSS性能评估的基本原理

如图1所示,当待评估PSS未投运时,称为开环系统,而当待评估PSS投运时,称为闭环系统。设d为系统等效扰动,y o(y c)为开环(闭环)系统在受到扰动后产生的能代表系统低频振荡特性的动态响应信号,y i,u i为PSS的反馈信号和控制输出信号,G o(s),H(s)分别为开环系统和待评估PSS的近似线性化系统传递函数,各信号之间的关系如下:

当PSS投入闭环运行时,按照线性叠加原理,则有:

将式(2)-(3)代入式(4),则有:

对于抑制低频振荡而言,目标是使得功率波动趋向于0,即r=0,进而有:

当系统发生扰动,导致某一模态出现功率振荡时,可令s=jω表示角频率为ω的功率振荡,则该振荡模态的动态过程可近似描述为:

对于特定的系统运行方式,即G o(jω),C i(jω)一定的条件下,如果PSS的增益固定(受限于控制能量约束),则可知:对于频率为ω的振荡模式,PSS相移满足以下条件时:

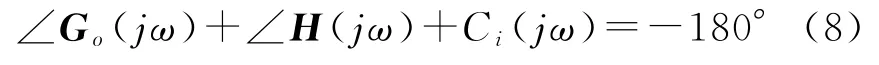
其振荡的幅值最小;换言之,该模式对于扰动有最好的鲁棒稳定特性;而且PSS的相移特性越接近于满足式(8),对应模式的振荡幅值越小。因此,可以通过在线分析PSS输入-输出的相移特性来检验PSS的效用,考虑到信号的偏差,设置相移区间为150°～210°,这就是在线评估PSS 的相移原理。

2 仿真分析

2.1 仿真分析系统

2.1.1 机组-电网模型

为验证机组非停工况下PSS调节性能,本节采用实际电网离线数据进行仿真分析。离线数据中的发电机、励磁系统、PSS、调速系统均按照实际电网模型建模,参数为工程实测参数,少数未实测机组采用典型参数,采用BPA 软件计算不同负荷水平时机组非停故障下PSS的调节性能。

2.1.2 励磁系统与PSS的模型及参数

机组励磁系统AVR 具有IEEE ST1A 标准模型,其传递函数如图2所示。

图2 IEEE ST1A 静态励磁系统

AVR 的典型参数为:TC=3 s,TB=4 s,TB1=0.06 s,TC1=0.03 s,KF=0,TF=1 s,KA=56.25,TA=0.02 s。

机组的PSS 具有IEEE PSS2B 标准模型,其传递函数如图3所示。

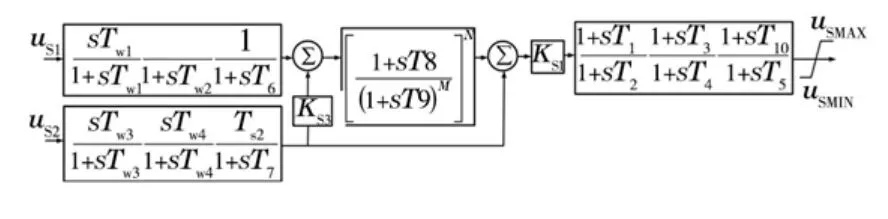
图3 IEEE PSS2B双输入电力系统稳定器

PSS的典型参数为:Ks1=7,Ks2=6.8,Ks3=1.2,T1=0.05 s,T2=0.19 s,T3=0.05 s,T4=0.19 s,T4=0.1 s,T5=0.1 s,T10=0,T6=0.2 s,M=2,N=1,Tw1=6 s,Tw2=6 s,Tw3=6,Tw4=6 s,T7=6 s,T8=0.6 s,T9=0.09 s;图中us1代表以转速偏差作为系统的反馈量,us2代表以功率偏差作为系统的反馈量,在本例中只取功率作为系统的反馈量。

2.2 仿真分析结果

在PSS参数确定的情况下,机组非停工况下PSS调节性能与励磁系统无补偿特性密切相关。而励磁系统无补偿特性对并列机组数量、并网电气距离、电网负荷水平、临近机组PSS投退等因素不敏感,对机组有功、无功出力影响显著[8]。本节仅对不同有功功率、无功功率情况下PSS的调节性能进行仿真分析。选取某发电厂作为研究对象,安装有2 台机组,其发电机额定有功功率为330 MW,额定无功功率为160 MVar。

2.2.1 机组额定有功功率时PSS性能分析

保持运行方式不变,发电机迟相运行,在有功功率为330 MW,无功功率为160 MVar工况下,切除1 号机组,分析2 号机组PSS 的调节性能。额定有功功率非停时机组仿真曲线见图4。

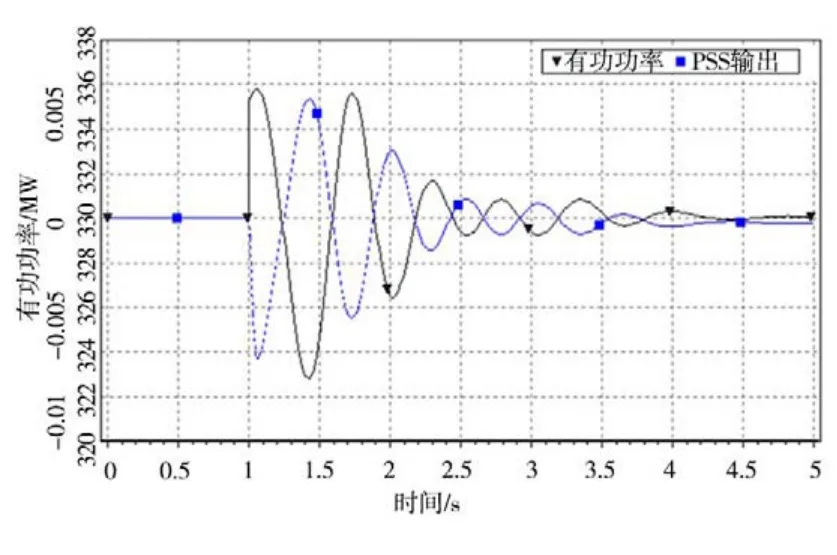
图4 额定有功功率非停时机组仿真曲线

由图4可知,有功功率振荡次数为3次,振荡频率为1.52 Hz,阻尼比为0.12,满足标准要求。此时有功功率第1次最大值时间为1.06 s,PSS输出第1次最大值时间为1.43 s,两者的相位差为201°,满足PSS相移区间的设定。

2.2.2 机组50%额定有功功率时PSS性能分析

保持运行方式不变,发电机迟相运行,在有功功率为165 MW,无功功率为80 MVar工况下,切除1 号机组,分析2 号机组PSS 的调节性能。50%额定有功功率非停时机组仿真曲线见图5。

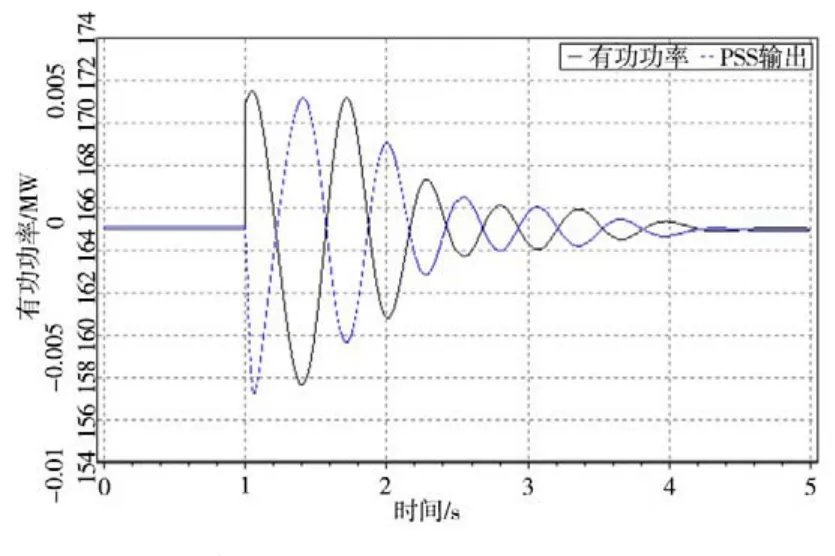
图5 50%额定有功功率非停时机组仿真曲线

由图5可知,有功功率振荡次数为3次,振荡频率为1.49 Hz,阻尼比为0.11,满足标准要求。此时有功功率第1次最大值时间为1.05 s,PSS输出第1次最大值时间为1.41 s,两者的相位差为193°,满足PSS相移区间的设定。

2.2.3 发电机进相时PSS性能分析

保持运行方式不变,发电机进相运行,在有功功率为165 MW,无功功率为-45 MVar工况下,切除1 号机组,分析2 号机组PSS 的调节性能。额定有功功率非停时机组仿真曲线见图6。

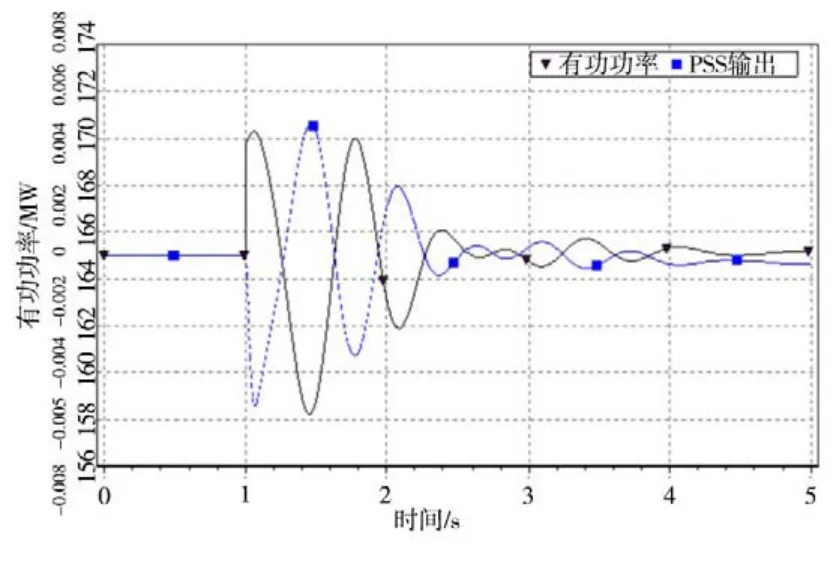
图6 额定有功功率非停时机组仿真曲线

由图6可知,有功功率振荡次数为3次,振荡频率为1.39 Hz,阻尼比为0.13,满足标准要求。此时有功功率第1次最大值时间为1.06 s,PSS输出第1次最大值时间为1.46 s,两者的相位差为200°,满足PSS相移区间的设定。

在发电机额定有功功率、50%额定有功功率、发电机进相3种负荷水平时,机组非停扰动下对PSS调节性能进行了分析,当有功功率与PSS输出相位差在设定的PSS相移区间时,PSS的调节性能满足标准要求,能够有效抑制低频振荡。

3 PSS性能评估的工程应用

3.1 机组非停概况

2019年3月4日11:16,河北省南部电网某热电厂1号机组跳闸,机组容量330 MW,原因为汽轮机DEH 主蒸汽阀门及调门异常关闭,汽包压力升高,汽包水位低保护动作切机。机组非停前,全网统调发购25 236 MW,1号机组故障前出力260 MW,占河北省南部电网统调发购的百分比为1.03%。由电气专业的发变组A 柜逆功率跳闸,24 ms后主断路器跳开,88 ms后灭磁断路器跳开,机组与系统解列。

3.2 PMU 装置录波分析

1号机组非停过程中,PMU 装置录取的2号机组的有功功率及PSS输出信号。正常情况下有功功率和PSS输出信号均出现小幅波动,有功功率波动为249～251 MW,波动幅值为2 MW,PSS输出信号波动为0～0.1 V,波动幅值为0.1 V。在11:14:19时,1号机组跳闸,2号机组有功功率和PSS输出信号均出现大幅波动。有功功率波动为247～253 MW,波动幅值为6 MW,PSS输出信号波动为-0.4～0.3 V,波动幅值为0.7 V。有功功率波动幅值扩大3倍,PSS输出信号波动幅值扩大7倍。有功功率和PSS输出信号相位差为162°,在PSS的有效相移区间内,PSS参数能够有效抑制本次低频振荡。

3.3 PSS性能试验验证

由于受到现场试验条件的限制,仅对本机振荡频率的PSS阻尼效果进行了验证。发电机并网运行,发电机有功功率为300 MW,无功功率为80 Mvar,PSS退出,将发电机TV 及TA 二次侧三相电压和三相电流接入WFLC电量分析仪中准备录波,在此情况下进行负载电压2%阶跃试验,同时启动WFLC 录波,记录有功功率的摆动次数。再将PSS投入,同样工况下重复以上试验。

PSS不投入时,有功功率摆动次数约为4次;PSS投入后,有功功率摆动次数约为1次。由此可知,有功功率的摆动次数减少,PSS对于本机振荡有明显的抑制作用。

4 结论

通过理论分析、仿真计算和现场试验相结合的方法,研究了基于WAMS系统数据的机组非停扰动下PSS调节性能的评估和参数校核方法。得出如下结论:

a.通过在线分析PSS输入-输出的相移特性即有功功率与PSS输出的相位差能够检验PSS的效用,相移可以设为150°～210°;

b.依据PSS输入-输出的相移特性评估PSS参数与进组有功功率、无功功率等因素不敏感;

c.经机组故障跳闸后WAMS系统数据的分析证实了应用PSS输入-输出的相移特性评估其参数切实可行。