一种基于时间序列模型的城市轨道交通客流量的预测数据分析

徐皓

（合肥职业技术学院，安徽 合肥 230000）

1 前言

城市轨道交通客流对地铁实际运营过程中的策略决策有重大影响。现阶段，国内各地铁公司虽有各种大客流的应急预案，但都有明显的滞后性。所以，近年来，国内各大城市都对地铁客流的预测展开了研究。其中，杭州地铁借助阿里云平台，由达摩院牵头，开展了一次“天池全球城市计算AI挑战赛-地铁客流量预测 大赛，用于甄选出适合杭州地铁的客流预测模型，为后来的运营管理提供数据支撑，可见客流预测越来越被人们所重视。

2 现有模型概述

常见的时间序列有平稳非平稳之分。其中，前者是序列的统计特征[均值E(Xt)、协方差Cov(Xt,Xs)、相关性不随时间变化而变化。非平稳时间序列，统计特征随着时间的变化而变化。

判断其是平稳还是非平稳序列，常用如下：（1）利用散点图进行平稳性检验；（2）利用样本自相关函数进行平稳性判断；（3）单位根检验等检验方法，此处选用最简单的曲线图来直观判定，实际效果见图1。

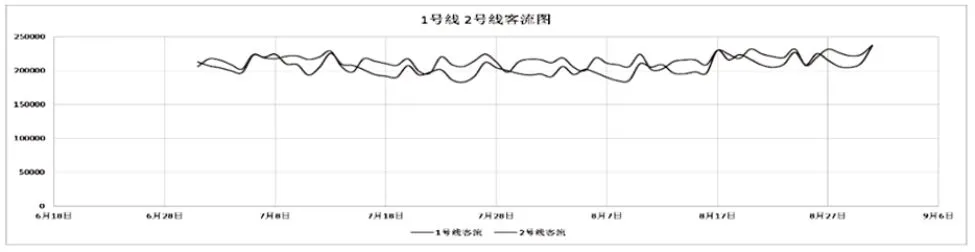
图1

2.1 时序模型的预处理

对于平稳非白噪声序列，它的均值和方差是常数。ARMA模型适用于此种序列。

对于非平稳序列，由于统计特征不稳定，首先转化成平稳序列，然后分析，常用ARIMA 模型。

2.2 几种时间序列模型的总结

（1）AR（自回归模型）：用变量历史数据对未来预测，该模型必须满足平稳性的要求。

如 果{εt} 为 白 噪 声， 服 从N(0,σ2)，a0,a1,...,ap(ap≠0) 为实数，就称p 阶差分方程：

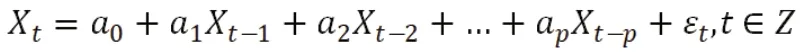
是一个p 阶自回归模型，简称AR(p)模型。自回归方法的优点是所需资料不多，可用自身变数数列来进行预测。但是这种方法受到一定的限制：如果自相关系数(R)小于0.5，预测结果偏离较大，不适用此类模型。

（2）MA（移动平均模型）：如果一个单变量时序数据{yt;t=1,2,...}，满足如下关系，则定义为MA 函数

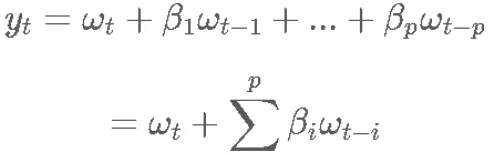
（3）ARIMA（p,d,q）差分自回归移动平均模型。AR 的含义为 自回归 ，p 参数表示自回归项数；I 表示差分的含义，d 为差分次数（阶数）；MA 为 滑动平均 ，q 为滑动平均项数。

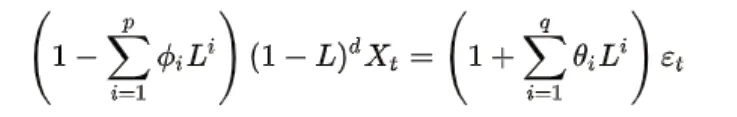
其中，L 是滞后算子（Lag operator）。

2.3 研究步骤

本次使用ARIMA 模型对客流量进行预测。一般情况下，城市轨道交通的客流量数据{at}是非平稳的，需要进行差分转化。

将记为差分算子，那么，有：

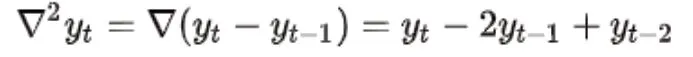
statsmodels 库提供适合ARIMA 模型的功能。可以使用statsmodels 库创建ARIMA 模型，如下所示：

通过调用ARIMA（）并传入p，d 和q 参数来定义模型。通过调用fit（）函数在训练数据上准备模型。可以通过调用predict（）函数并指定要预测的时间或索引的时间索引来进行预测。我们将ARIMA 模型与整个Shampoo Sales 数据集相匹配，并检查残差。

我们可以使用ARIMAResults 对象上的predict（）函数进行预测。如果我们在训练数据集中使用前150 个观测值来拟合模型，那么，用于进行预测的下一个时间步骤的索引将被指定给预测函数，如start=1，end=150。这将返回一个包含预测的一个元素的数组。如果我们执行任何差分（在配置模型时d＞0），我们也希望预测值在原始比例中。这可以通过将typ 参数设置为’levels’值来指定：typ=’levels’。我们可以将训练数据集拆分为训练集和测试集，使用训练集来拟合模型，并为测试集上的每个元素生成预测。考虑到差异的先前时间步长和AR 模型的观察依赖性，需要滚动预测。执行此滚动预测的一种粗略方法是在收到每个新观察后重新创建ARIMA 模型。

最终的预测结果如图2。

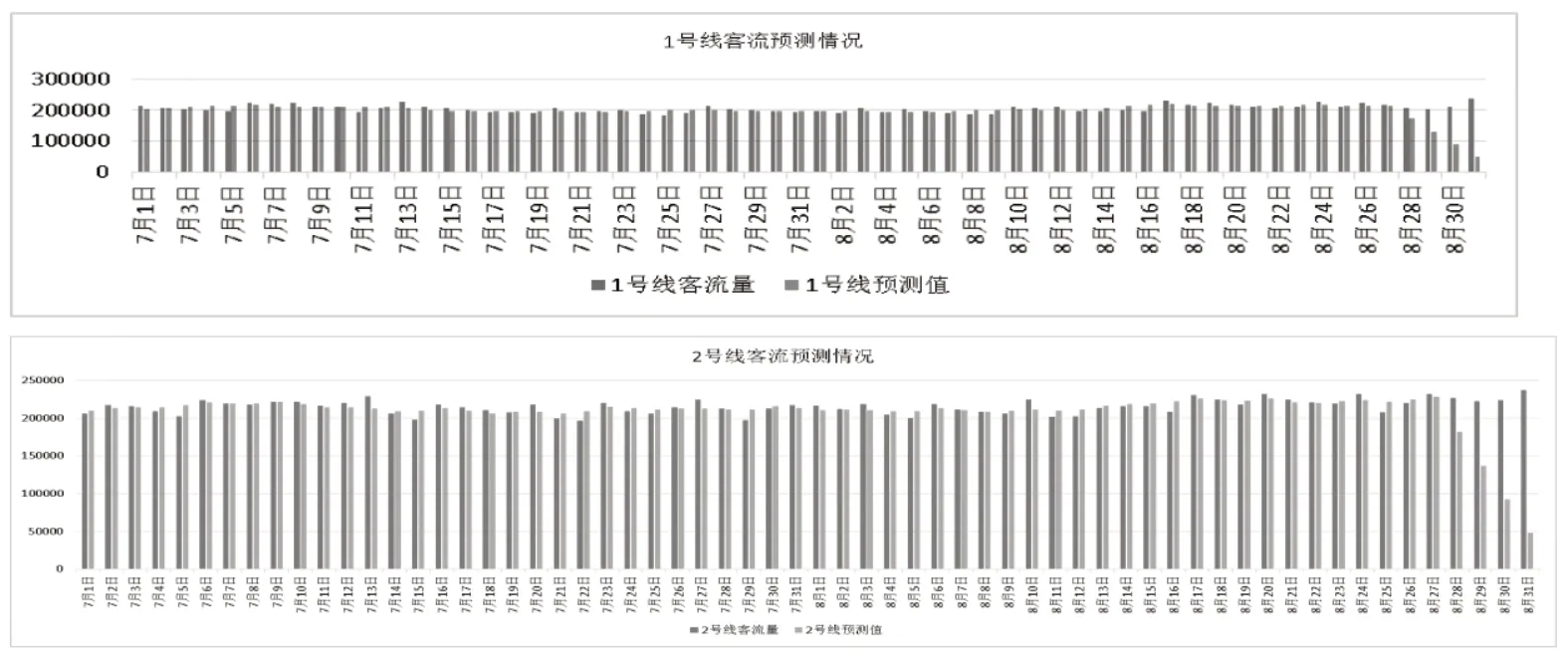
图2