高空带电机器人轨迹跟踪与控制研究

胡仕成，陈志高，黎新齐

(中南大学 机电工程学院，湖南 长沙 410083)

由于高压电网络线路长、分布广、线路环境复杂、作业空间狭小等特点，给人工带电作业开展带来巨大困难，高空带电机器人的出现可以有效地解决上述困难。通过自主和遥控操作灵活切换能替代人完成复杂环境下的支线线路引线搭接等高危工作。

由于工作环境的复杂性和控制系统存在的滞后性，导致了高空带电机器人工作效率和工作精度的低下，要实现机器人的自动化和智能化，需要一种高空带电机器人轨迹跟踪控制方法，提高控制系统的响应速度、控制精度。

相关专业人士提出了一种作业平台的轨迹跟踪控制方法，通过对液压阀控系统特性研究，设计了相应的PID控制器优化其系统，使得工作斗位置跟踪波动范围小于±200mm，采用PID 控制、负反馈以及前馈的复合控制来实现臂架直线轨迹控制。

针对高空带电机器人臂架控制问题，本文通过建立高空带电机器人臂架三维模型和臂架系统简图，对臂架进行运动学分析，推导出抓手相应轨迹下两个变幅液压缸的运行轨迹，并提出了一种PID 优化控制方法来提高控制系统的响应速度、控制精度。并在MATLAB/Simulink 环境下进行仿真，比较优化前后系统的响应速度和控制精度。

1 高空带电机器人的臂架控制系统总体设计

1.1 臂架三维模型

高空带电机器人主要包括臂架系统和液压控制系统，臂架系统包括底座1、竖直臂2、水平杆3、伸缩杆4、摆动杆5、抓手6 组成。臂架系统如图1 所示。

1.2 臂架运动学建模及轨迹跟踪

根据臂架系统原理，建立臂架结构简图，如图2 所示：将高空带电机器人工作臂简化为四关节的机器人手臂，采用D-H 坐标法对臂架四个杆件建立相对坐标系，并引入连杆扭角α，连杆长度a，关节转角θ，关节距离d 四个参数来描述每个杆件的相对位置，建立其臂架的运动学数学模型。

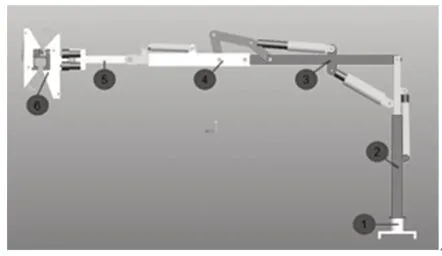
图1 高空带电机器人三维模型

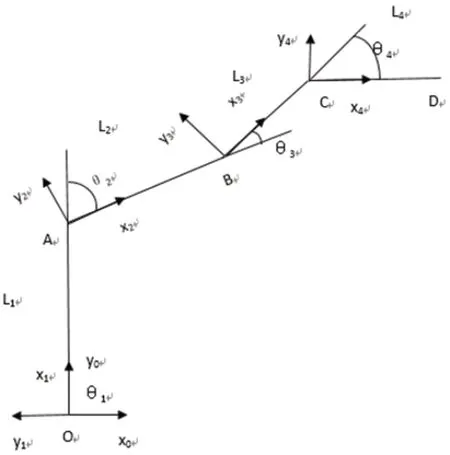
图2 D-H 坐标系

如图2 所示，以O 点作为作为整体参考坐标原点，四个杆件从原点开始编号，分别依次为1、2、3、4 号杆件，杆件长度分别对应记为L1、L2、L3、L4，以各杆件首端位置作为局部坐标系的原点，即图2 中的O 点、A 点、B 点、C 点，杆件与其局部坐标系x 轴之间的夹角为关节转角θi，i=1，2，3，4；di为接续公垂线的偏距，即相邻杆件的轴向的距离。运用机器人学，根据Craig D-H 坐标系，得到杆件坐标系下相邻杆件之间的位姿矩阵：其分别表示杆件首端相应于局部坐标系的转换矩阵。

根据各个相邻关节的坐标变换矩阵，可以得到第四关节相对于整体坐标原点变换矩阵。

由于建立的D-H 坐标系是Craig D-H 坐标系，所以还需要建立第四关节末端D（即高空带电机器人抓手位置）相对于整体坐标原点的变换矩阵，首先，D 点相对于局部坐标系4 的位置变换矩阵为：

由此坐标系可以得出D 点相对于整体坐标系原点的变换矩阵为：

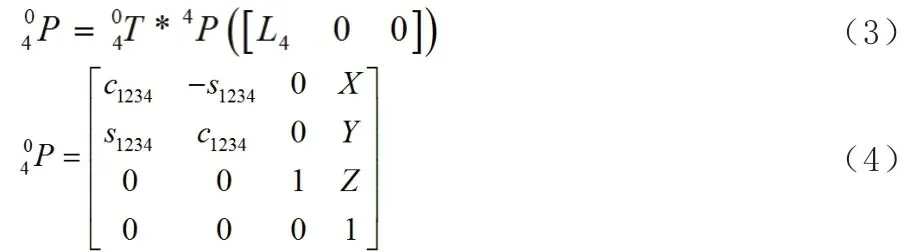
由式（8）可以得出臂架关节转角θ 与抓手在基坐标系间的几何关系：

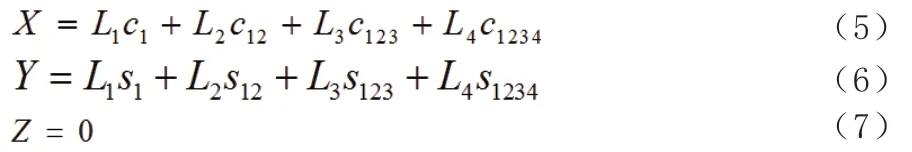
故高空带电机器人臂架末端抓手坐标为：

为方便输出图形，只关注遍历算法，不用思考计算输出图形的坐标位置，因此不考虑在命令行中打印二叉树，而是采用DOT图形描述语言。DOT是纯文本图像描述语言，文件扩展名通常是.dot，需要有专门的程序处理这些文件并将其渲染成为图片。Graphviz是贝尔实验室开发的一个开源的图像可视化的软件，它使用dot作为脚本语言，然后使用布局引擎来解析此脚本，并完成自动布局。

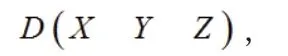
高空带电机器人的最大作业高度为：

最远工作长度为：

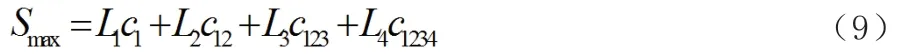
机器人工作臂的 D-H 参数表，如表1 所示。

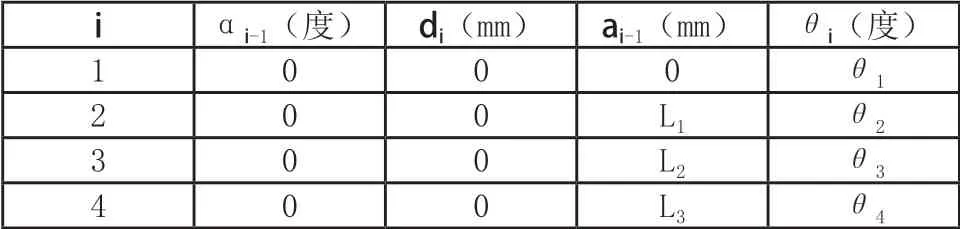
表1 臂架Craig D-H 参数表

2 臂架液压数学模型的建立

高空带电机器人臂架液压控制系统采用的闭环控制，由高空带电机器人臂架采用的是变幅液压控制系统，该系统是通过对电液比例换向阀的控制进而实现液压缸的工进和返回的。接下来，将根据电液比例系统原理进行数学模型的建立，推导出该系统的传递函数。

电液比例阀的数学模型为：

参考文献得阀控液压缸的传递函数可以近似为：

位移传感器的数学模型视为比例环节：

综上所述，电液比例系统的传递函数为：

臂架变幅液压系统数学模型的相关参数数值如表2 所示：

表2 数学模型相关参数

3 MATLAB/Simulink 建模及仿真分析

为了验证PID 的控制效果，建立PID 优化控制系统仿真模型，仿真模型如图3 所示，模型包括目标响应环节、实际响应环节和PID 响应环节三个部分组成，主要对其三种环节的仿真结果进行分析，其中目标响应环节和实际响应环节的参数设置与上文相同，PID 响应环节首先要对PID 控制器的三个参数进行设置，PID 参数设置方法包括试凑法、Ziegler—Nichols 整定法、临界比例度法、衰减曲线法等方法。该仿真通过试凑法对PID 控制器的比例系数、积分系数和微分系数不断进行调节，观察系统响应曲线，获得系统最优响应。

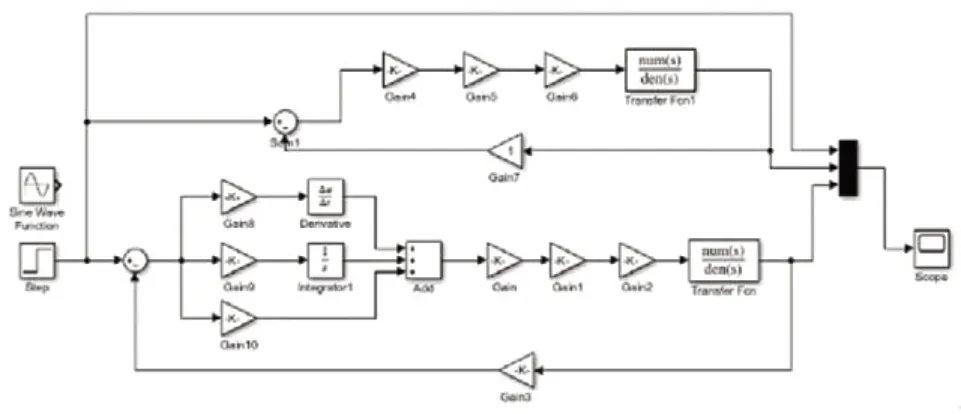
图3 变幅液压系统PID 优化仿真模型

经过多次对PID 控制器三个系数的调节和响应数据曲线的比较，发现在比例系数取值为15、积分系数取值为0.1、微分系数取值为0.001 的情况下，系统响应最优，系统调节时间较短，滞后程度较低，PID 优化后的控制系统在给定阶跃控制信号后，1 秒达到期望值，相对优化前的响应滞后7 秒，系统响应速度提高了85.7%，但只是在响应期间，有轻微的波动，由于对系统不会产生较大影响，可以忽略。

PID 优化后的控制系统在给定正弦信号后，系统响应曲线与目标曲线非常接近，只是有0.2 秒的滞后，其响应的峰值也完全相同，相对于优化前的系统响应，在响应时间上和控制信号的期望响应上面都有较大的改善，综合性能有了很大提高。

4 结语

根据高空带电机器人臂架运动特点，首先，简化臂架结构，应用D-H 坐标法建立臂架运动学模型，得到机器人抓手的运动数学模型。其次，臂架液压控制系统与PID 控制相结合，可以有效解决系统响应滞后的问题，阶跃控制信号在PID 优化控制后，系统响应时间缩短85.7%，正弦控制信号较优化前系统响应缩短至0.2 秒，响应峰值也与目标值完全相同。

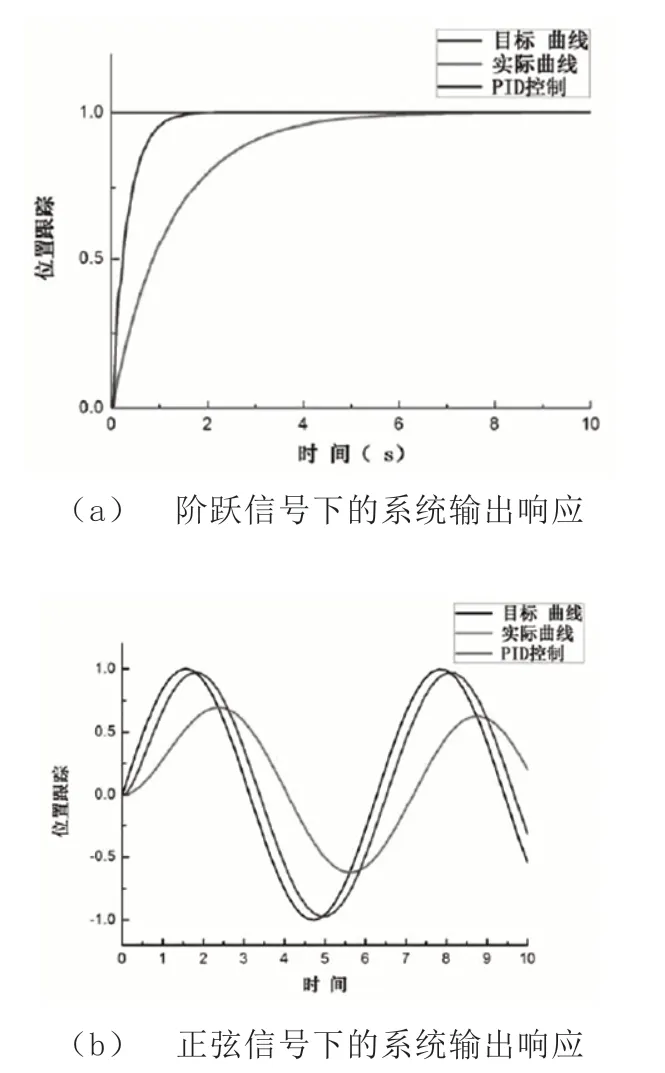
图4 PID 优化前后的系统响应对比图