改进的GM(1,1)模型在地铁运营隧道的沉降预测分析

杨恒昆 贾文超

（1 深圳市市政设计研究院有限公司；2 广东省工程勘察院）

0 前言

在地铁运营过程中，随着隧道建成年限的增加，由于区域性地面沉降、隧道周边基坑开挖、隧道渗漏、列车荷载等因素的影响，隧道沉降会持续增大，继而影响地铁正常运行、乘客乘坐舒适性，严重的不均匀沉降将直接造成地铁本身结构的变形，甚至引发安全性问题[1]。在地铁隧道长期运营过程中，不间断出现的隧道沉降问题日益引起相关单位的重视，因此，通过科学合理的方法对隧道沉降问题进行预测预防具有重要的理论和实践意义。

灰色理论认为一切随机变量是在一定范围内变化的灰色量，对灰色量的处理不是找概率分布和求统计规律， 而是根据数据处理的方法来找出数据间的规律，因而只要求较短的观测资料就可处理， 这就和时序分析、多元分析等概率统计模型要求较多的观测资料很不一样[2]。

GM(1，1)模型具有十分广泛的应用领域。是工程监测中最常用的一种预测模型，许多文献对此进行了大量的研究， 但也存在一些预测精度不高的情况。因此，对GM(1，1)模型进行深入仔细的研究，提高其模型的精度及其适应性， 具有非常重要的理论意义和实际意义[3]。本文利用基于残差改正的GM(1，1)模型对地铁运营隧道长期沉降的变化趋势进行预测分析，得到了良好的精度效果及可靠性。

1 灰色系统GM（1，1）原理

在传统的GM（1，1）模型中，设非负且离散的数据序列为：

X(0)=﹛x(0)（1），x(0)（2），x(0)（3），……x(0)（n）﹜，式n 为序列长度，对X(0)进行一次累加生成，得X(1)=﹛x(1)（1），x(1)（2），x(1)（3），……x(1)（n）﹜，对X(1)序列建立一阶微分方程[4]。

式⑴即为GM(1，1)模型，在该式中，α、u 为灰参数，其白化值为依据最小二乘法可求得：

对X(1)作紧邻均值生成：

式⑵中矩阵B 及向量：

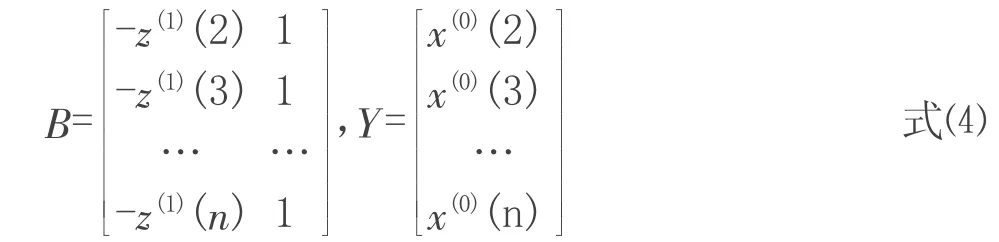
将利用最小二乘原理求得的â 代入式⑴中，可求解出微分方程为：

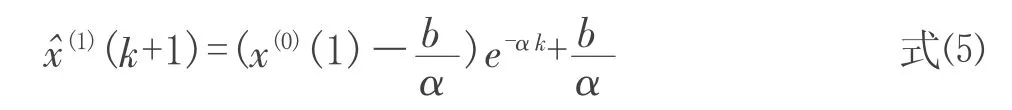
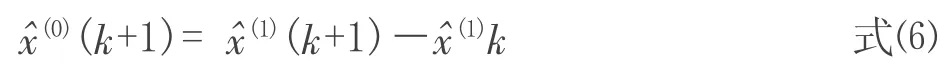
对上文所述建立得GM(1，1)模型进行残差大小检验、后验差检验等，残差大小检验是对模型值和实际值进行逐点检验；后验差检验是对残差分布的统计特征进行检验，它由后验差比值及小概率误差概率P 共同确定[5]。由上文中GM（1，1）模型预测得到数据序列为：

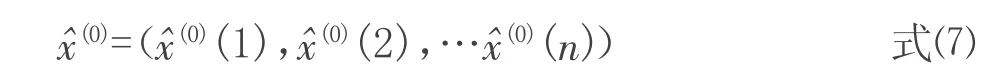
计算残差序列ε(k)=x(0)(k)－x(1)(k)得：

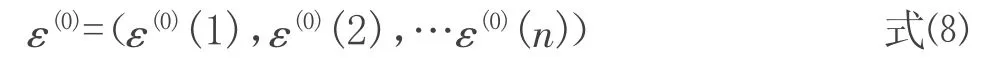
记原始数据序列x(0)及残差数据系列ε(0)的方差分别为：

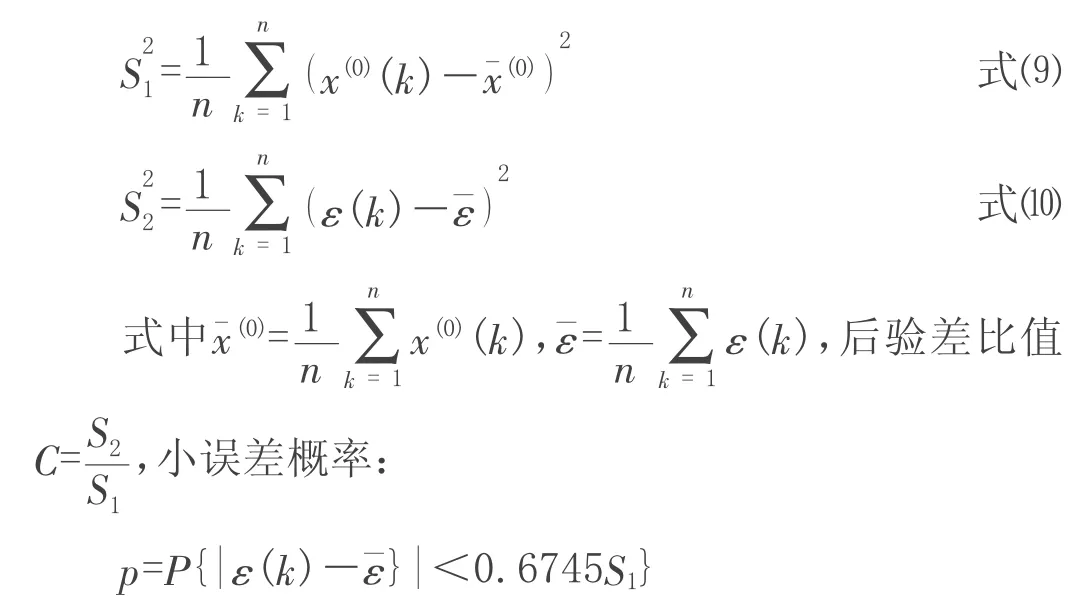
2 基于残差修正的GM（1，1）模型改进

计算残差序列ε(k)=x(0)(k)－x(1)(k)得ε(0)=(ε(0)(1)，ε(0)(2)，…，ε(0)(n))。若k0存在，并合理定义k0，其满足①k≥k0，ε(0)(k)的符号一致；②n－k0≥3，则称(|ε(0)(k0)|，|ε(0)(k0+1)|，…，|ε(0)(n)|) 为可建模残差尾段[6]，记为：

对该残差尾段数据序列重复进行GM（1，1）模型预测，则其残差修正值为：

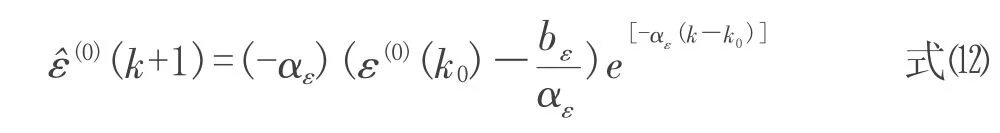
将残差修正值改正至原预测值中，经过残差修正的累减还原式GM（1，1）模型见式⒀：

3 工程实例

工程实例选取广州地铁某线路过江段左线道床D1沉降监测点及右线道床D2 沉降监测点2020 年4 月～2020 年8 月监测数据进行建模及预测分析，数据如表1所示。

利用数学软件matlab2016a 对沉降数据进行GM（1，1）模型建模分析，传统的GM(1，1)计算结果如表2、表3 所示。

利用残差改进后的GM(1，1)模型计算结果如表4、表5。

表1 沉降监测数据

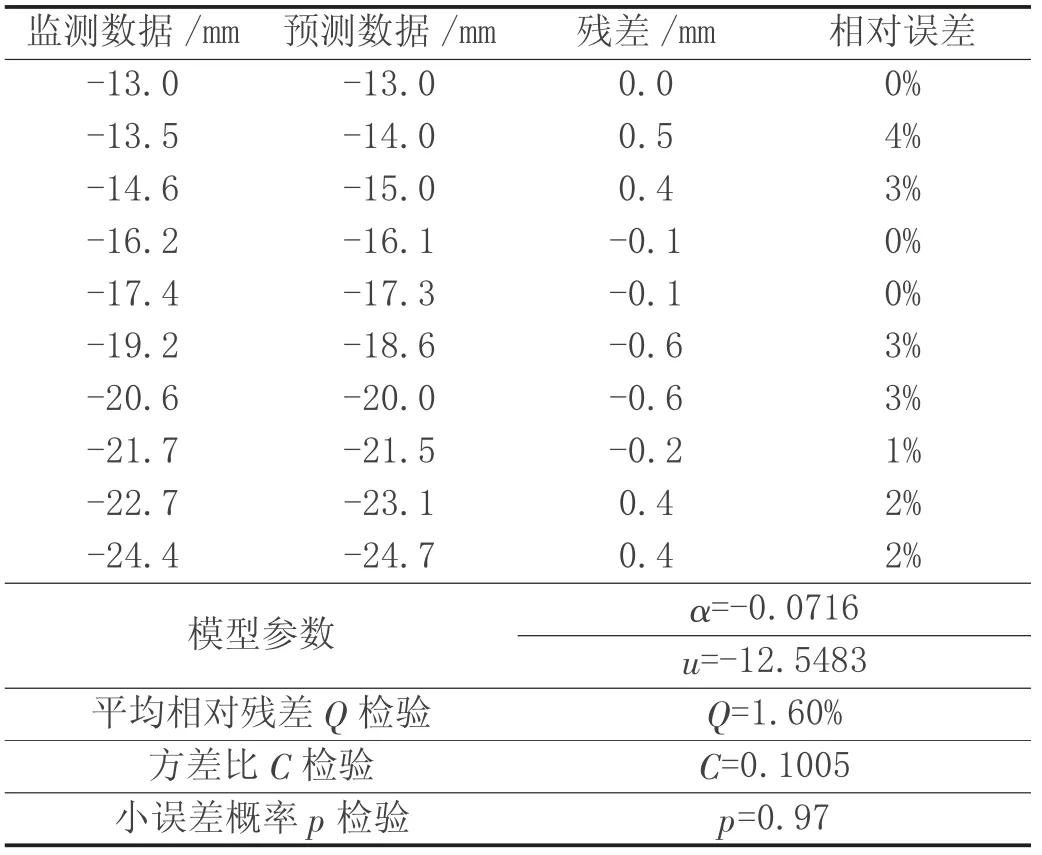
表2 传统模型下D1点沉降数据计算结果

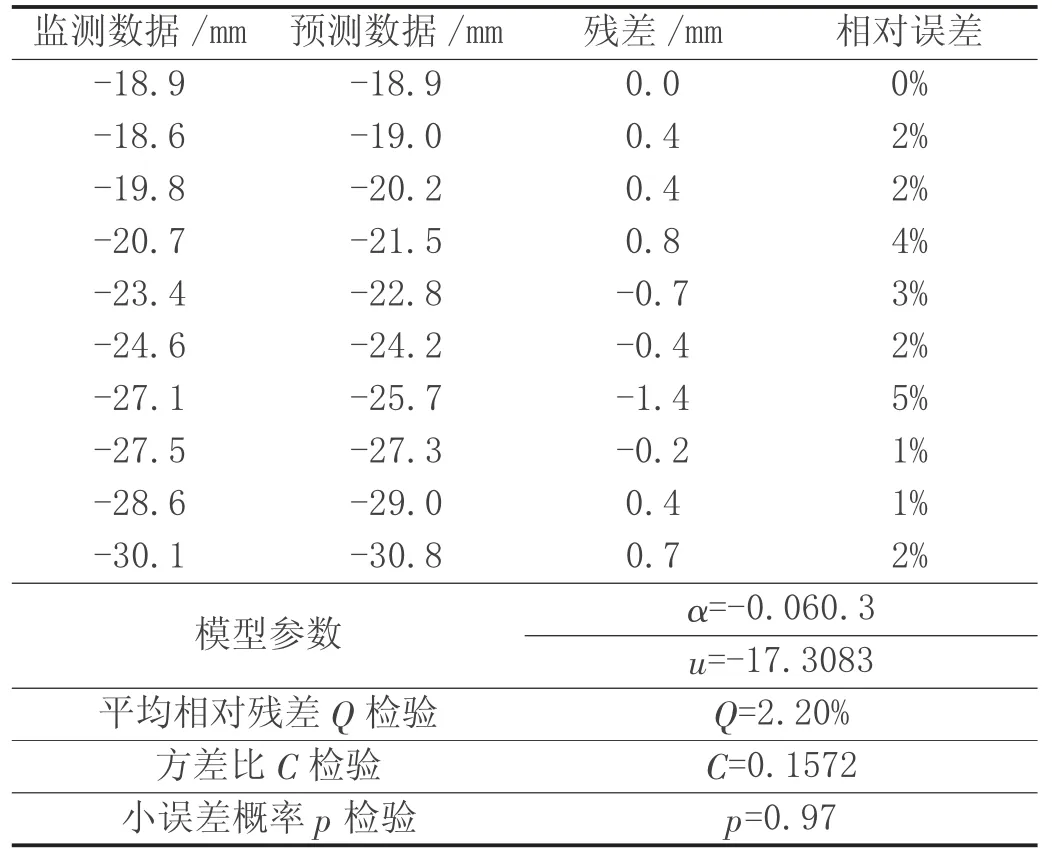
表3 传统模型下D2 点沉降数据计算结果

传统的GM(1，1)模型及利用残差改进后的GM(1，1)模型沉降预测曲线对比如图1、图2 所示。

从表4 及表5 的数据预测结果可看出，传统的GM(1，1)模型在D1、D2 点的预测结果与实际监测数据相比平均相对误差分别为1.60%及2.20%，利用残差改进后的GM(1，1)模型在预测结果上的平均相对误差分别为0.78%及0.92%，在其方差比C 检验及小误差概率p 检验中，残差改进后的GM(1，1)模型的表现均优于传统的GM(1，1)模型，从图1 及图2 的曲线图对比结果上，残差改进后的GM(1，1)模型预测数据相对于传统的GM(1，1)模型也更贴近于实际监测数据。

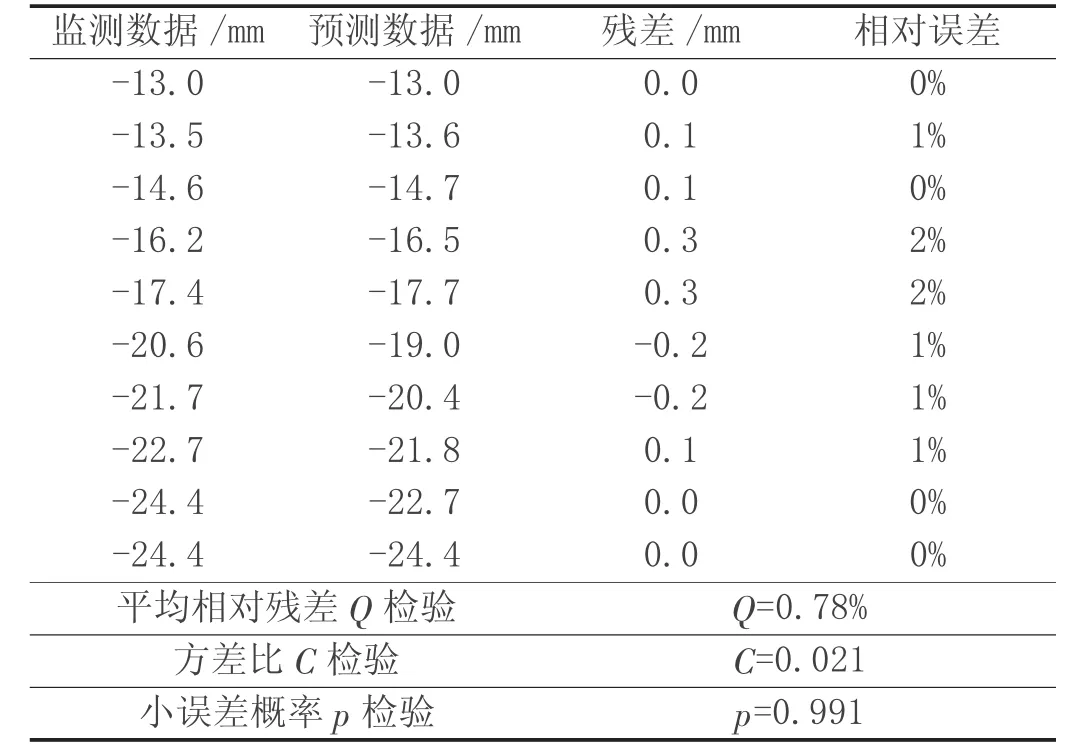
表4 改进后模型下D1点沉降数据计算结果

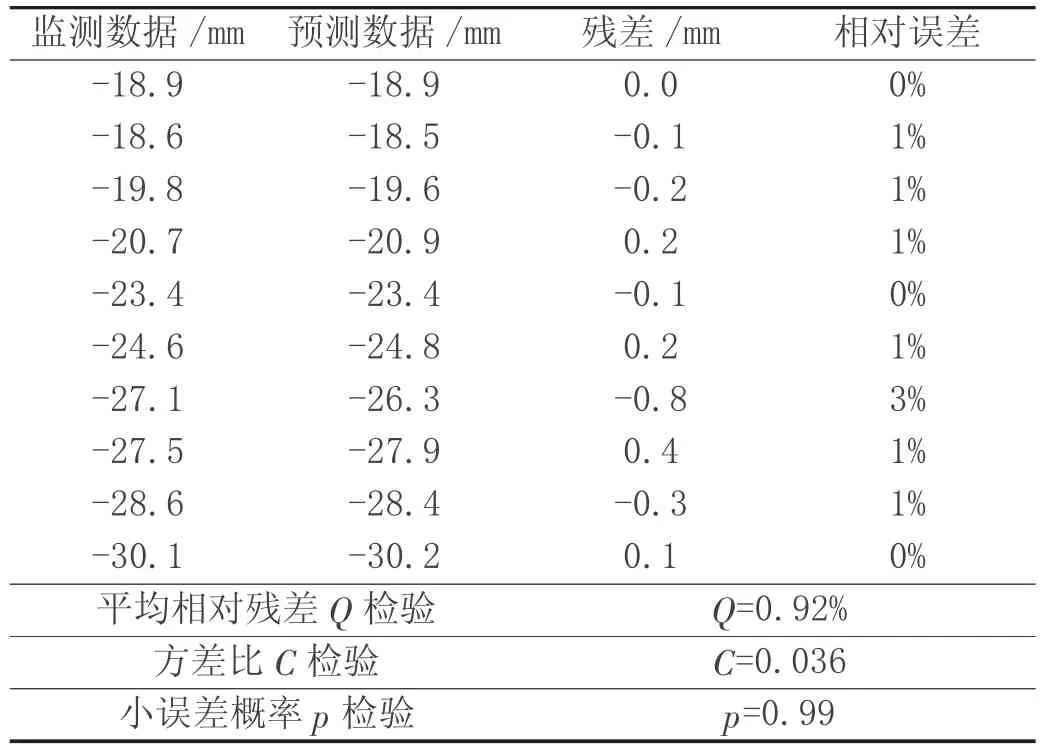
表5 改进后模型下D2 点沉降数据计算结果

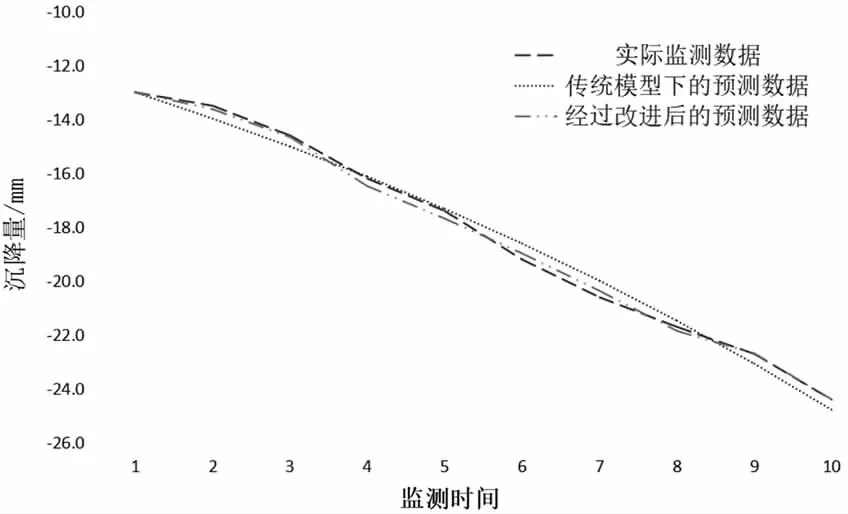
图1 D1 点沉降预测曲线

4 结论

本文介绍了灰色系统GM(1，1)模型的原理及建模方法，并通过实例对残差修正的GM(1，1)模型与传统的GM (1，1) 模型进行比较分析，结果表明残差修正GM(1，1)模型能够更准确地预测监测点的沉降变化规律和趋势，相对于传统的GM(1，1)模型其精度更高，可靠性更好，基于残差修正的GM(1，1)模型在工程监测领域具有良好的适用性，可广泛应用。