库底淤积层对重力坝动力损伤的影响研究

陈金杭

(南京水利科学研究院，南京瑞迪建设科技有限公司，江苏 南京 210029)

1 概述

传统的重力坝抗震设计中，动水作用主要采用Westergaard[1]提出的基于刚性坝面获得的近似解答。其推导时，假设了水体不可压缩和库底不吸收边界，不能考虑库水可压缩性及库底沉积层与坝体及地基之间的相互作用，这难以真实地反映出库水及沉积层对多耦合体系的影响。事实上，水库蓄水后，随着时间推移，库水中的泥沙会在库底逐渐沉积并在坝前形成一定厚度的沉积层，会吸收一些地震能量，降低大坝的地震响应。国内外许多研究学者就库底淤积层的吸收特性方面做了很多工作：Cheng[2]研究了淤积层吸能效应的影响。闫毅志[3]将库底淤积层视为两相多孔弹塑性介质，分析了淤积层对重力坝地震响应的影响。王怀亮[4]考虑坝体为弹塑性材料，研究了库底淤积层对碾压混凝土重力坝地震响应的影响。

尽管已有一些学者做了库底淤积层吸能效应的研究[2- 7]，但在以上这些研究中，坝体混凝土材料通常采用弹塑性本构模型来模拟。混凝土作为一种复合型的准脆性材料，采用塑性损伤力学的方法更能真实反映出混凝土材料超出其抗拉压强度时所表现出的强非线性性质。然而，至今还没有学者将库底淤积层的吸收效应与重力坝损伤特性联系起来进行研究。本文将坝体模拟为塑性损伤材料，参考文献[8]将淤积层模拟为黏性、大密度可压缩流体，结合Koyna重力坝工程实例，建立能够真实反映库水及库底淤积层对重力坝多耦合体系的地震损伤仿真分析模型。以库底淤积层厚度作为变量，研究了不同淤积层厚度对重力坝多耦合体系动力损伤演化的影响。

2 计算理论与计算方法

2.1 混凝土塑性损伤模型

混凝土塑性损伤模型本构关系[9]

(1)

损伤后的弹性模量表示为

(2)

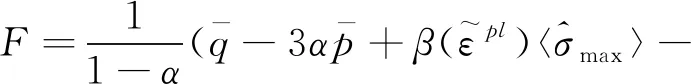
(3)

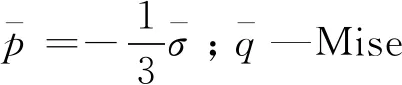
2.2 库水-淤积层模型控制方程

对于坝库耦合系统，忽略库水黏性，动水压力p可按下式计算[8]

(4)

库底沉积层模拟为黏性、可压缩重流体，连续方程为

(5)

运动方程

(6)

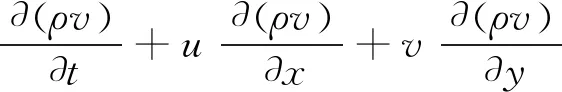
(7)

式中，t—时间；ρ—流体密度；μ—动力粘性系数；ω—激励频率；c—水体中声音的传播速度；u、v—流体x和y方向的速度分量；fx、fy—体积力在x和y方向上的分量。

3 模型验证

为验证本文采用的黏性重流体模拟库底淤积层的正确性，本文取与文献[7-8]相同的计算模型，模型为一理想三角形坝，如图1所示。坝体密度2483kg/m3，泊松比0.2，性模量27.5GPa；基岩岩体密度2643kg/m3泊松比0.33，弹性模量27.5 GPa；采用Abaqus中的声学单元来模拟库水可压缩性，水体密度为1000kg/m3，体积模量为2.0GPa；库底淤积层的运动黏性系数为4.5[12]，淤积层初始密度为1656kg/m3，体积模量为3.33GPa。

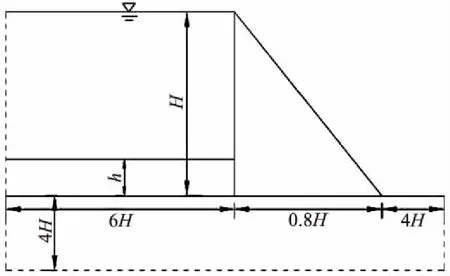
图1 坝体-库水-淤积层-地基模型

在地震动输入方面，考虑0.01地震能量向无限远域传播影响，地基四周施加弹簧阻尼单元，地震波从底部人工边界处垂直入射。图2为库底淤积层厚度为h=0.1H时，本文模型计算得到的坝顶坝基的相对加速度反应与文献[7- 8]得到的计算结果比较。图2中横轴为无量纲频率比值(ω为输入的激励频率，ω1为坝体基频为4.61Hz)；纵轴ap为坝顶的相对加速度反应，aH为坝基的相对加速度反应。本文的计算结果与文献[7-8]中计算结果较为符合，验证了本文采用模型的正确性。坝体在分别受到水平地震动和竖直地震动时，坝顶点加速度频率响应有所不同，耦合系统在受到水平向简谐地震动激励时，坝顶加速度响应只有一个峰值；而受到垂直向简谐地震动激励时，出现了三个峰值。

4 库底淤积层对重力坝动力损伤演化的影响

4.1 坝体-坝基-库水-淤积层有限元模型

1967年位于印度的Koyna混凝土重力坝遭受6.5级地震，震后调查资料显示坝身出现多条水平裂缝如图3所示，并在下游折坡处出现渗漏水现象。本文选取Koyna重力坝的一个挡水坝段进行有限元分析，模型地基范围上、下游、深度方向各取2倍坝高，建立坝体-坝基-库水-淤积层耦合模型，如图4所示。

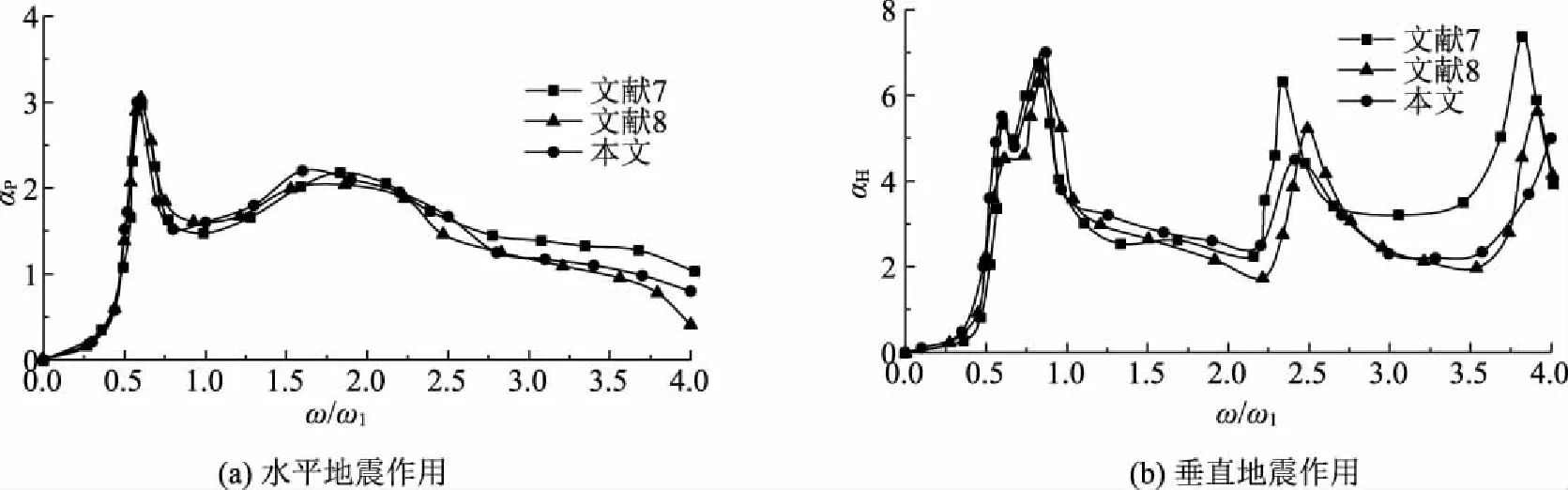
图2 本文模型与文献[7- 8]计算结果的比较(h=0.1H)

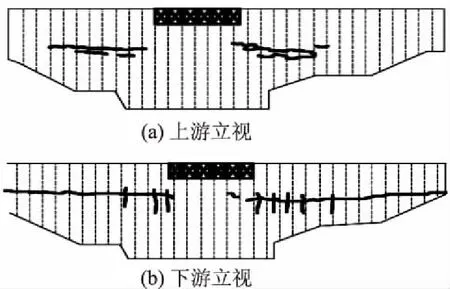
图3 Koyna坝体震害

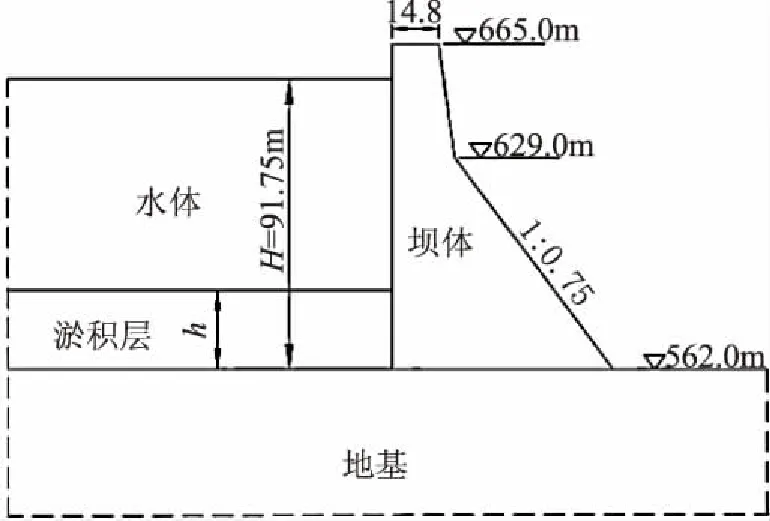
图4 坝体-坝基-库水-淤积层模型

地震波时程为Koyna坝1976年实测地震记录，如图5—6所示。考虑地震能量向无限远域传播影响，地基四周施加弹簧阻尼单元[10]。库水模拟为可压缩理想流体，密度1000kg/m3，体积模量取2.14GPa；库底淤积层模拟为黏性、大密度可压缩流体，初始密度为1656kg/m3，体积模量3.33GPa，淤泥黏性系数按文献[8]取值。计算采用的坝体混凝土参数为：混凝土动弹模31GPa，动态抗拉强度2.90MPa，2630kg/m3，泊松比0.2。地基假定为线弹性，弹性模量20GPa，泊松比0.2。

图5 水平向地震波加速度时程曲线

图6 竖直向地震波加速度时程曲线

4.2 淤积层厚度对重力坝动力损伤的影响

在考虑体系地震能量向远域逸散效应后[10]，进行坝体-库水-淤积层-坝基体系的地震响应损伤分析。计算中分别假定库底淤积层厚度h取值为0、10、20、30m，分别对应四种工况a、b、c、d，相应的h/H值分别为0、0.109、0.219、0.329。通过对比模型损伤区域、能量耗散指标两个方面来研究不同淤积层厚度对耦合体系的损伤影响。

4.2.1对塑性损伤区域的影响

计算结果如图7所示。重力坝坝体损伤主要集中在折坡处高程和坝踵处附近，坝体混凝土在下游折坡处高程附近出现贯穿损伤区。通过对比不难发现，随着库底淤积层厚度的增加，坝体损伤程度逐渐减轻，这是由于厚淤积层吸收了由坝基传至上部结构的部分能量所致。另从图中可以看出，当库底淤积层厚度h=0时(图7(a))，坝体上游面有两条贯穿损伤带，坝体下游面在折坡处出现贯穿损伤带，当库底淤积层厚度增加到h=30m时(图7(d))，坝体混凝土损伤区域缩小，坝体上游面有一条贯穿损伤带，另一条损伤带接近消失。对比图7(a)—7(d)发现淤积层厚度变化对坝踵处损伤影响并不十分显著。

4.2.2对位移的影响

对位移的影响，图8是不同库底淤积层厚度下，坝体关键点顺河向位移时程曲线，从图8中可以看出，与库底淤积层厚度为零时相比，随着淤积层厚度增加，观测点上游面坝顶点和下游折坡处顺河向位移均有所减小，以淤积层厚度为零时观测点的最大顺河向位移为基准，淤积层厚度h分别增大至10、20、30m时，上游面坝顶点最大顺河向位移分别减小了2.4%、7.1%、10.25%，下游折坡处最大顺河向位移分别减小了4.4%、8.9%、12.1%。

4.2.3对能量耗散指标的影响

本文从损伤耗能和塑性应变耗能[11- 12]两个耗能指标对四种工况进行比较分析。如图9所示，地震作用下，在t=2.83s时刻坝体混凝土开始出现损伤，在t=4.18s时刻坝体出现较大损伤，随着地震持时继续增加，坝体损伤耗能和塑性耗能值趋于稳定。在损伤耗能方面，当库底淤积层厚度为0时，坝体损伤耗能最大，库底淤积层厚度与坝体损伤耗能成反比关系。与损伤耗能情况类似，在塑性应变耗能方面，坝体塑性应变耗能随着库底淤积层厚度的增加而减小[13- 15]。

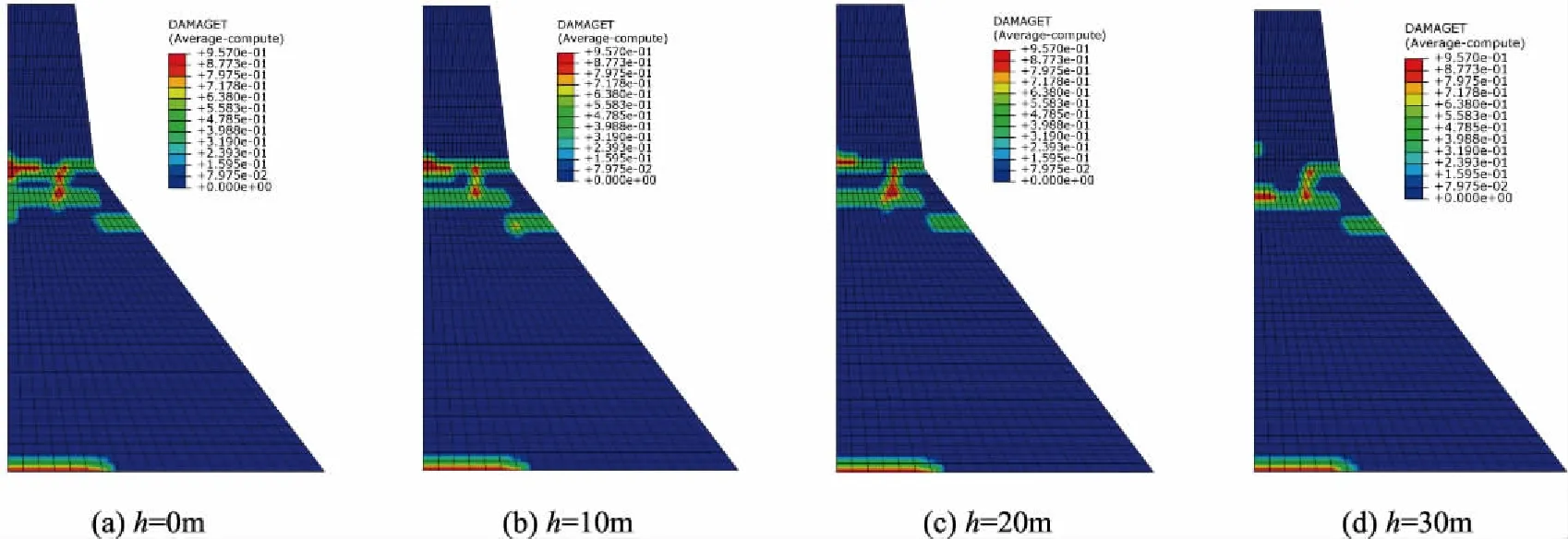
图7 重力坝损伤区云图

图8 坝体关键点顺河向位移时程曲线

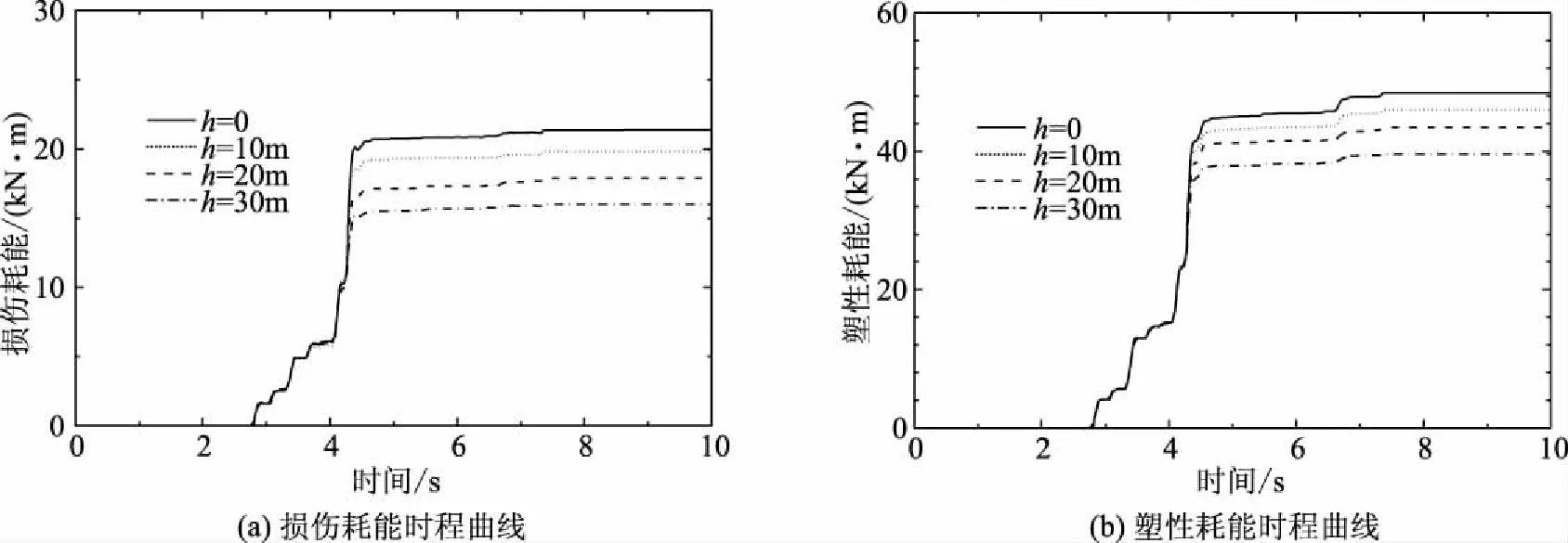
图9 重力坝体系耗能时程曲线

从图10的不同工况下坝体损伤耗能和塑性耗能的指标对比可以看出：地震作用下，坝体的塑性耗能值要大于损伤耗能值。损伤耗能方面，假定以淤积层厚度为零时的损伤耗能值为基准，淤积层厚度h从0分别增大至10、20、30m时，体系损伤耗能分别减小7.10%、16.25%、24.91%。塑性应变耗能方面，同样以淤积层厚度为零时的塑性应变耗能为基准时，淤积层厚度h增大至10、20、30m时，体系塑性应变耗能分别减小4.95%、10.33%、18.18%。若以坝体损伤耗能和塑性损伤耗能两项指标和为基准，可以得出b、c、d三种工况下综合耗能分别减小了5.67%、12.17%、20.28%。

5 结论

本文将坝体混凝土模拟为塑性损伤材料，将库底淤积层模拟为黏性、可压缩重流体，建立了坝体-库水-淤积层-坝基系统的多耦合损伤力学模型。以库底淤积层厚度为变量，在四种工况下分别对模型在地震动荷载作用下的动力响应进行分析，研究不同淤积层厚度对重力坝耦合体系动力损伤演化的影响，结果表明:

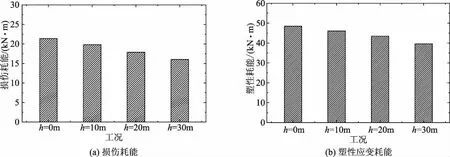
图10 不同工况下坝体耗能

库底淤积层能一定程度上降低重力坝耦合体系的动力损伤响应。在地震作用下，淤积层厚度变化对坝体折坡处高程的混凝土损伤影响较大，对坝踵处混凝土损伤影响并不十分显著。随着淤积层厚度增加，地震作用下大坝位移响应有所减小，其中淤积层h厚度由0 m增大至30m时，上游面坝顶点和下游折坡处最大顺河向位移分别减小了10.25%和12.1%。

综合比较库底淤积层厚度对坝体损伤耗能和塑性耗能指标的影响得出：当淤积层厚度较低时(例如h/H<0.2)，可不考虑库底淤积层的影响；当h/H增加至0.2时，此时体系综合耗能指标约减小10%，应对库底淤积层有所考虑。