体内无粘结预应力混凝土梁受弯承载力计算模型研究
于晓光,穆卓辉,邢国华
(1.长安大学 公路学院, 陕西 西安710064; 2.长安大学 旧桥检测与加固技术交通行业重点实验室, 陕西 西安710064; 3.内蒙古自治区交通建设工程质量监督局, 内蒙古 呼和浩特 010051)
对体内无粘结预应力混凝土梁的承载性能进行分析时,由于预应力筋与混凝土界面没有粘结作用并且可以相对滑动,使得预应力筋与混凝土之间不存在应变协调关系,不符合平截面假定,导致该类混凝土梁中预应力筋的应力较难精确计算.
众所周知,预应力筋的极限应力主要是由张拉控制应力和极限应力增量两部分组成,其求解过程主要是应力增量的求解.目前,国内外主要采用两类方法来对预应力筋的极限应力增量进行计算[1]:第一类是基于大量试验数据,统计回归分析得出影响极限应力增量计算的主要参数,提出预应力筋应力增量的经验计算方法,如我国行业标准《无粘结预应力混凝土结构技术规程》[2]和杜拱辰、宋永发等提出的极限应力增量[3-4]的计算方法;第二类是引入一些的相关基本假定,通过理论分析,建立一个多参数的极限应力增量表达式,然后借助试验结果确定相关参数的合理取值(范围),最后提出极限应力增量的修正计算方法,该类方法侧重于理论分析[5-8].此外,申同生等[9]提出了用能量法求解极限应力增量的计算理论,即利用最小势能原理,求解获得整个系统的总势能,然后利用能量变分原理得到力筋的极限应力增量,该方法主要用于无粘结预应力混凝土连续梁在均布荷载作用下无粘结预应力筋极限应力增量的计算,目前尚未得到广泛应用[10-12].
本文在已有研究基础上,基于预应力混凝土梁的整体变形、更加合理地简化了梁曲率分布,获得无粘结预应力筋在混凝土梁发生破坏时的应力,通过截面分析法提出了无粘结预应力钢筋混凝土梁的受弯承载力计算模型,并与国内外77组预应力混凝土梁试件的试验结果进行了对比.
1 抗弯承载力计算模型的提出
对于体内无粘结预应力筋混凝土梁,预应力筋的应变增量不取决于梁截面的应变,而是取决于预应力混凝土梁的整体变形.梁体的变形可由沿梁跨度方向上的曲率分布来计算.因此,确定预应力筋的应变大小首先应确定预应力混凝土梁在荷载作用下的曲率分布.
图1(a)为计算跨径为L的简支梁在两点对称荷载作用下的受力示意图,极限状态下该简支梁的简化曲率分布如图1(b)所示.曲率分布的简化主要围绕曲率的分布范围,最早学者忽略弯剪段曲率分布,只通过考虑纯弯段的极限曲率分布来计算混凝土梁的整体变形,但大量的试验研究[13-14]表明:无粘结预应力混凝土梁除了在纯弯段出现垂直裂缝外,在纯弯段的外也存在大量斜裂缝,即弯剪段也应考虑曲率分布.
各国学者以此现象为基础提出了等效塑性区域的概念,1991年Harajli 和 Hijazi[13]基于试验结果提出两点对称荷载作用下预应力混凝土梁的等效塑性区的长度为:La=L0+2Lp.式中L0=L/f,通常集中荷载作用下f=∞;三分点加载下f=3;均布荷载作用下f=6;Lp为纯弯段以外的塑性铰长度,它是钢筋屈服后,继续加载而产生较大的塑性变形.上述等效塑性区计算公式中L0可由梁的计算跨径和荷载形式得出,但是等效塑性铰长度Lp的取值存在较大分歧.
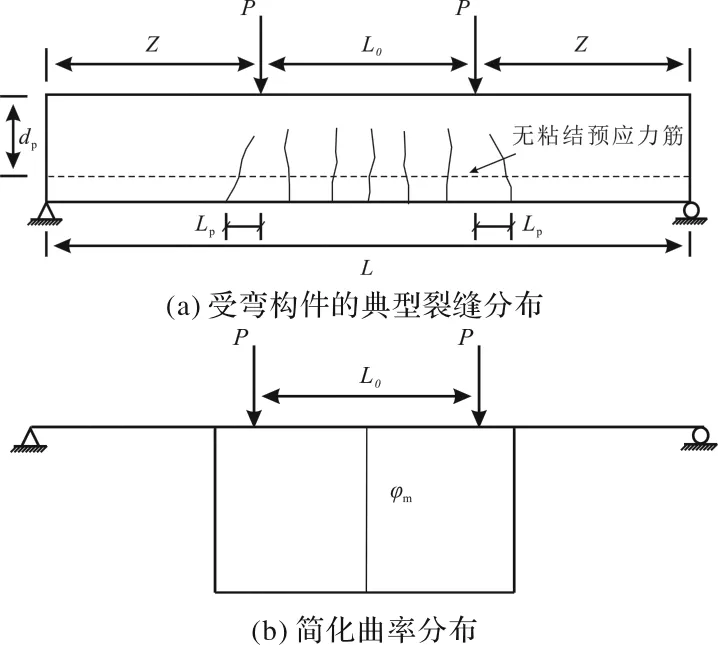
图1 对称集中荷载作用下无粘结预应力混凝土梁Fig.1 Simply supported concrete beam prestressed with unbonded tendons under four-point loading
Baker[5]基于试验研究,考虑钢筋种类和混凝土强度影响系数等因素后提出的等效塑性铰长度计算公式为
Lp=0.8k1k2(Z/dp)x
(1)
其中:k1为考虑钢筋类型的系数,若为软钢取0.7,若为硬钢取0.9;k2为考虑混凝土强度的影响系数;若fcu=13.8~41 N/mm2,k2=0.6~0.9;Z为临界截面到反弯点的距离;dp表示预应力筋重心至受压区边缘的距离;x为极限状态时截面折算受压区高度.
Corley[15]通过试验研究,同时考虑临界截面到反弯点的距离Z和梁的尺寸影响,提出的等效塑性铰的长度计算公式为
(2)
式中:Z为支座到加载点的距离;h为梁高.
Mattock[16]等进一步对Corley提出的关于塑性铰长度的表达式进行了修正,修正后塑性铰的长度计算公式为
Lp=0.5dp+0.05Z
(3)
上述简化的曲率分布模型,虽然可以对预应力混凝土梁进行承载性能分析,但是仍忽略了塑性区外的曲率分布,计算得到的预应力筋应力增量值尚不够精确[13].本文在文献[14]的基础上,对预应力混凝土梁沿跨度方向的裂缝分布特点(见图2(a))进行深入剖析,简化后的梁曲率分布如图2(b)所示.图2(b)中实线为预应力混凝土梁的实际曲率分布,虚线为理想化的曲率分布.假定在弯剪段曲率分布为线性分布,A(C)点曲率为开裂曲率;在塑性铰长度内仍为线性曲率分布,B(D)点曲率即纯弯段极限曲率;纯弯段曲率分布简化为矩形分布.具体将预应力混凝土梁曲率分布分解为三部分,即加载点之间距离L0,塑性铰长度Lp,支座到塑性铰边缘Lj,对这三部分分别积分,即可得到与预应力筋同一高度处混凝土梁沿跨度的总应变.

图2 无粘结预应力混凝土梁的曲率分布Fig.2 Curvature distribution for unbonded pretressed concrete beam
2 预应力混凝土梁极限承载力计算
对预应力混凝土梁正截面承载力计算时,梁破坏截面采用图3所示的应力状态.为了简化计算,受压区混凝土的理论应力图形采用等效矩形应力图形代换,图中β为矩形应力图受压区高度x与中和轴高度c的比值[17].
(4)
式中:f′c为混凝土圆柱体抗压强度,f′c=0.8fcu,fcu为混凝土立方体抗压强度.
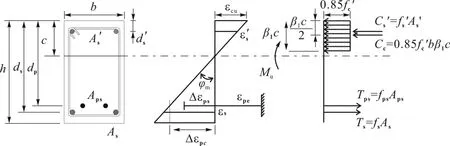
图3 无粘结预应力混凝土梁截面应力及其合力Fig.3 Stresses and forces of unbonded prestressed concrete beam cross section
在无粘结预应力混凝土梁受弯承载力的计算分析过程中,采用的基本假设如下:
(a)两点对称荷载作用下混凝土梁的截面应变除无粘结预应力筋外,均符合平截面假定;
(b)预应力混凝土梁极限破坏形式为混凝土压溃破坏,即破坏时梁顶缘混凝土达到其极限压应变εcu=0.003后压溃,非预应力受拉纵筋屈服,受压钢筋处于弹性工作应力状态;
(c)梁开裂后,忽略受拉区混凝土的作用;
(d)无粘结预应力筋为理想弹性材料,即混凝土梁发生破坏时,预应力筋仍处于弹性阶段;
(e)忽略无粘结预应力筋与孔道之间的摩擦力.
假定体内无粘结预应力混凝土梁破坏时,预应力筋仍处于弹性阶段,则预应力筋的应力增量为
Δfps=EpΔεps
(5)
其中:Δfps为无粘结预应力筋的应力增量,Ep为预应力筋的弹性模量,Δεps为无粘结预应力筋的应变增量.
荷载作用下无粘结预应力筋的应力增量与混凝土梁的整体变形有关,可以通过纵向变形协调条件,即在加载过程中无粘结筋的总伸长应与其周围混凝土的总变形相等的条件来求得,从而将求解无粘结预应力筋极限应力增量的问题转化为求解无粘结预应力混凝土梁的极限变形问题.
图3中任意截面处预应力筋周围混凝土的应变增量记为Δεpc,则预应力混凝土梁的伸长量为

(6)
其中:ls为预应力筋的伸长量;l为混凝土梁中预应力筋的长度;应变增量Δεpc可按下式计算.
Δεpc=φx(dp-cx)
(7)
其中:φx为沿梁跨度方向任意截面x处的曲率;cx为截面x处中性轴高度.
2.1 预应力梁的开裂曲率
为了获得预应力混凝土梁的简化曲率分布,需首先计算出混凝土梁的开裂曲率.
开裂曲率计算时,混凝土单轴向受压应力-应变本构关系采用Rüsh模型,即
(8)
其中:ε0为峰值应变,取ε0=0.002;ecu为极限压应变,取ecu=0.003.
混凝土的开裂应变为
εcr=ftk/Ec
(9)
其中:ecr为混凝土开裂时对应的应变;ftk为混凝土轴心抗拉强度;Ec为混凝土的弹性模量.
由于混凝土的抗拉强度很低,故混凝土梁开裂时所有钢筋仍处于弹性状态.根据平截面假定,当受拉区混凝土开裂时,梁受压区混凝土的最大压应变εc、受压钢筋应变ε′s1、受拉钢筋应变εs1分别为
(10)
(11)
(12)
其中:c1梁开裂时的中性轴高度,d′s为受压钢筋重心至受压区混凝土边缘的距离;ds为受拉钢筋重心至受压区混凝土边缘的距离.
预应力混凝土梁开裂时,加载点附近尚未形成塑性铰区,且弯剪段变形甚小,忽略不计,可只考虑加载点之间的梁体变形对预应力筋的影响,故无粘结预应力筋应变增量Δεps1为
(13)
其中:h为混凝土梁截面高度;L0为混凝土梁加载点之间的距离.
根据上述混凝土的本构关系,可求得混凝土梁开裂时,受压区混凝土最大压应力sc,由于该值较小,受压区混凝土应力分布可简化为三角形分布.忽略受拉区混凝土的贡献,根据力的平衡,可得
Cc+Cs=Ts+Tpt
(14)
1/2σcbc1+A′sEsε′s=AsEsεs+Aps(EpΔεps1+fpe)
(15)
其中:b为混凝土梁截面宽度;A′s为受压钢筋截面面积;Es为钢筋弹性模量;As为受拉钢筋截面面积;Aps为无粘结预应力筋截面面积;Ep为无粘结预应力筋的弹性模量fpe为无粘结预应力筋的有效预应力.
将式(10)~(13)代入公式(15)中,可求得混凝土梁开裂时对应的受压区高度c1,进而可计算得到混凝土梁的开裂曲率.
(16)
2.2 极限状态下无粘结预应力筋应力求解
极限状态下无粘结筋的总伸长应与其周围混凝土的总变形相等,因此对简化的曲率分布(图2(b))中L0,Lp,Lj三个区域积分,求得与预应力筋周围混凝土的总变形量,即为预应力筋的总伸长量.
(17)
(18)
ls3=φm(dp-c)L0
(19)
其中:ls1、ls2、ls3分别为Lj、Lp、L0区域内无粘结预应力筋周围混凝土的总应变,Lj为图2(b)中支座到A(C)段的距离,Lp为塑性铰的长度图2(b)中AB(CD)段,本文选用式(3)计算;φm为极限状态下混凝土梁的平均曲率,φm=εcu/c,εcu为梁受压区混凝土压溃时的应变,取ecu=0.003,c为预应力梁破坏时的中性轴高度.
将式(17)~(19)代入式(20)中,可得混凝土梁破坏时无粘结预应力筋周围混凝土的总应变,即无粘结预应力筋的总伸长量为
ls=ls1+ls2+ls3
(20)
相应地,混凝土梁破坏时无粘结预应力筋的平均应变Δεps、无粘结预应力筋的应力增量Δfps、无粘结预应力筋的应力fps分别为
Δεps=ls/L
(21)
Δfps=EpΔεps
(22)
fps=Δfps+fpe
(23)
2.3 无粘结预应力混凝土梁极限承载力求解
试验表明[3,18-20]:无粘结预应力混凝土梁中除了预应力筋因与周围混凝土发生滑移而不满足平截面假定外,其受力特性仍具有钢筋混凝土梁的一般特点,受弯承载力计算时仍可采用截面分析法.
图3为体内无粘结部分预应力钢筋混凝土梁的承载力计算简图.当受压区混凝土压溃时,非预应力受拉钢筋屈服,受压钢筋处于正常工作应力状态,预应力筋仍处于弹性阶段.根据平截面假定,受压钢筋应变ε′s为
(24)
由力的平衡,式(24)中梁破坏时混凝土受压区高度c可通过式(25)确定,为
Ac2+Bc+C=0
(25)
其中
A=0.85f′cbβ1
B=A′sE′sεcu+Asfy+Apsfps
C=-A′sEsd′sεcu
因此,无粘结预应力混凝土梁跨中截面极限弯矩Mu为

(26)
基于前述计算过程,先初步给出混凝土受压区高度c初值(取梁截面高度一半),计算出预应力筋应力增量和钢筋应力,检验各内力是否满足平衡方程.若满足,则可根据公式(26)求得极限弯矩Mu;若不满足,用二分法重新调整受压区高度c,重复上述步骤直到满足.
计算流程如图4所示,可通过Matlab软件编制程序实现.
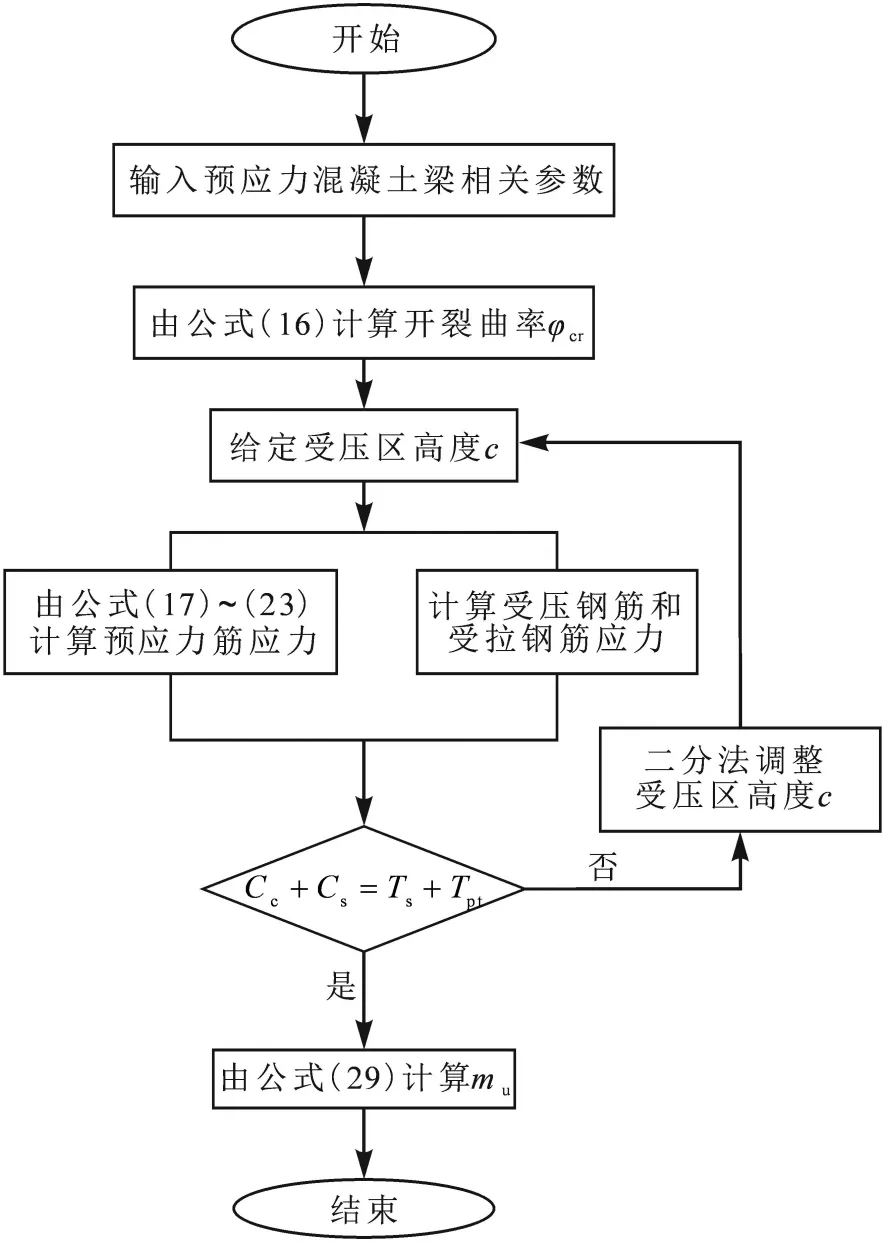
图4 受弯承载力计算流程图Fig.4 Flow chat for the calculation of flexural bearing capacity
3 模型验证
为了验证本文建议模型对体内无粘结预应力混凝土梁受弯承载力分析的适用性,对国内外77根[3,4,13,19,21-24]无粘结预应力混凝土梁的抗弯承载力进行理论分析,并将计算结果与美国ACI 318规范的计算模型[25]及其他模型[21]的计算结果进行了对比,抗弯承载力试验值与计算值的对比情况如表1所示,具体统计情况见图5.
从表1和图5可以看出:无粘结预应力混凝土梁受弯承载力的试验值与计算值之比的平均值为1.047,方差为0.077,变异系数为0.073,二者吻合较好;与其他计算模型的计算结果相比,本文建议计算模型较真实地反映了预应力混凝土梁的曲率分布,可更准确的计算无粘结预应力混凝土梁的抗弯承载力.
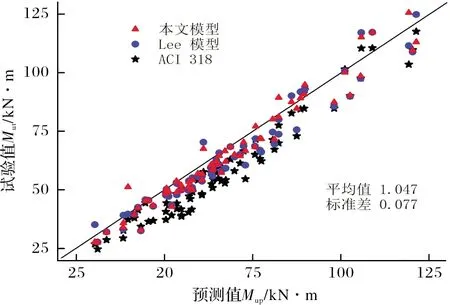
图5 受弯承载力的试验值与计算值Fig.5 Test values and predicted values of the flexural strength
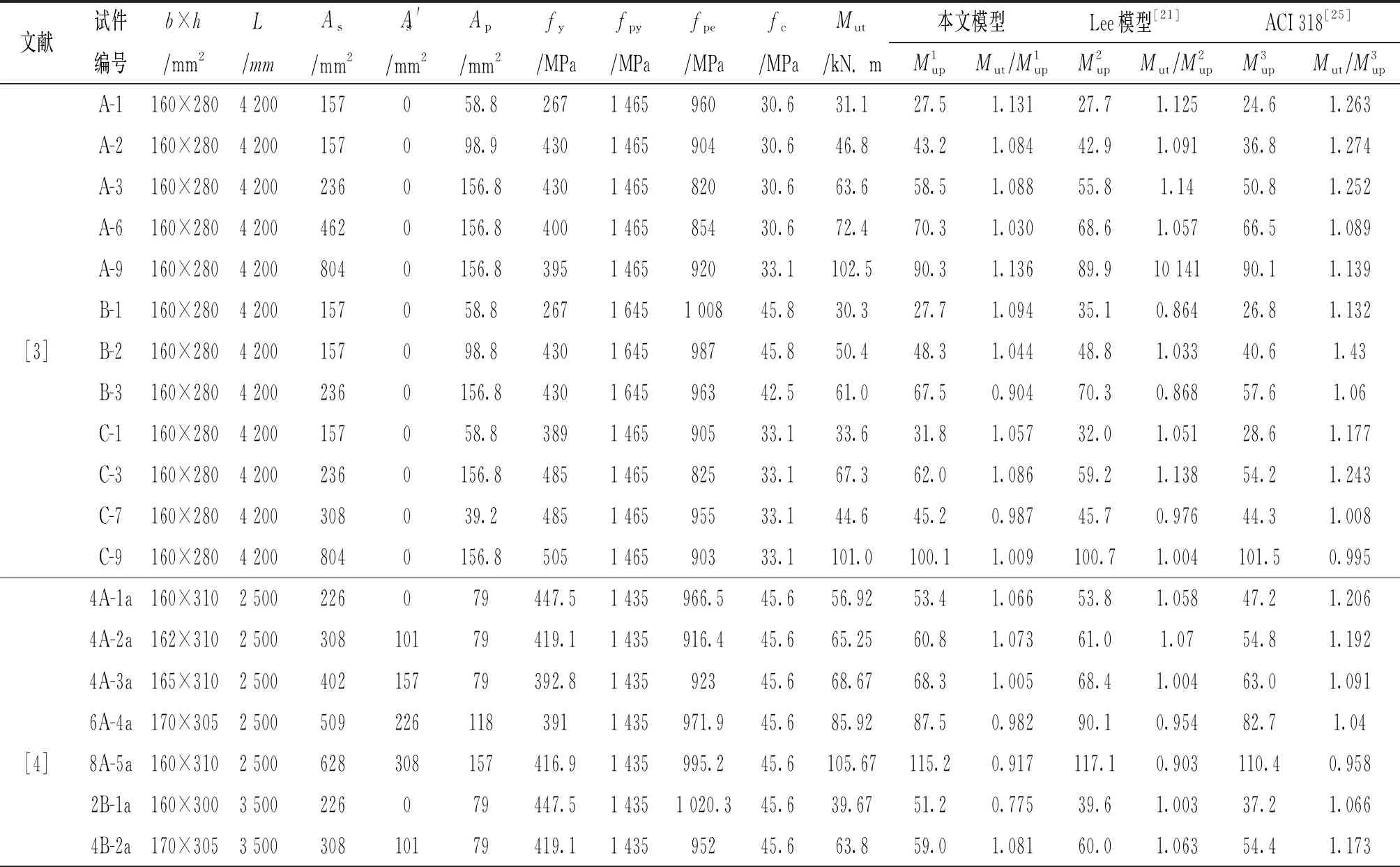
表1 无粘结预应力混凝土梁抗弯承载力试验结果与计算结果对比Tab.1 Comparison of flexural strength between test results and prediction results of unbonded prestressed reinforced concrete
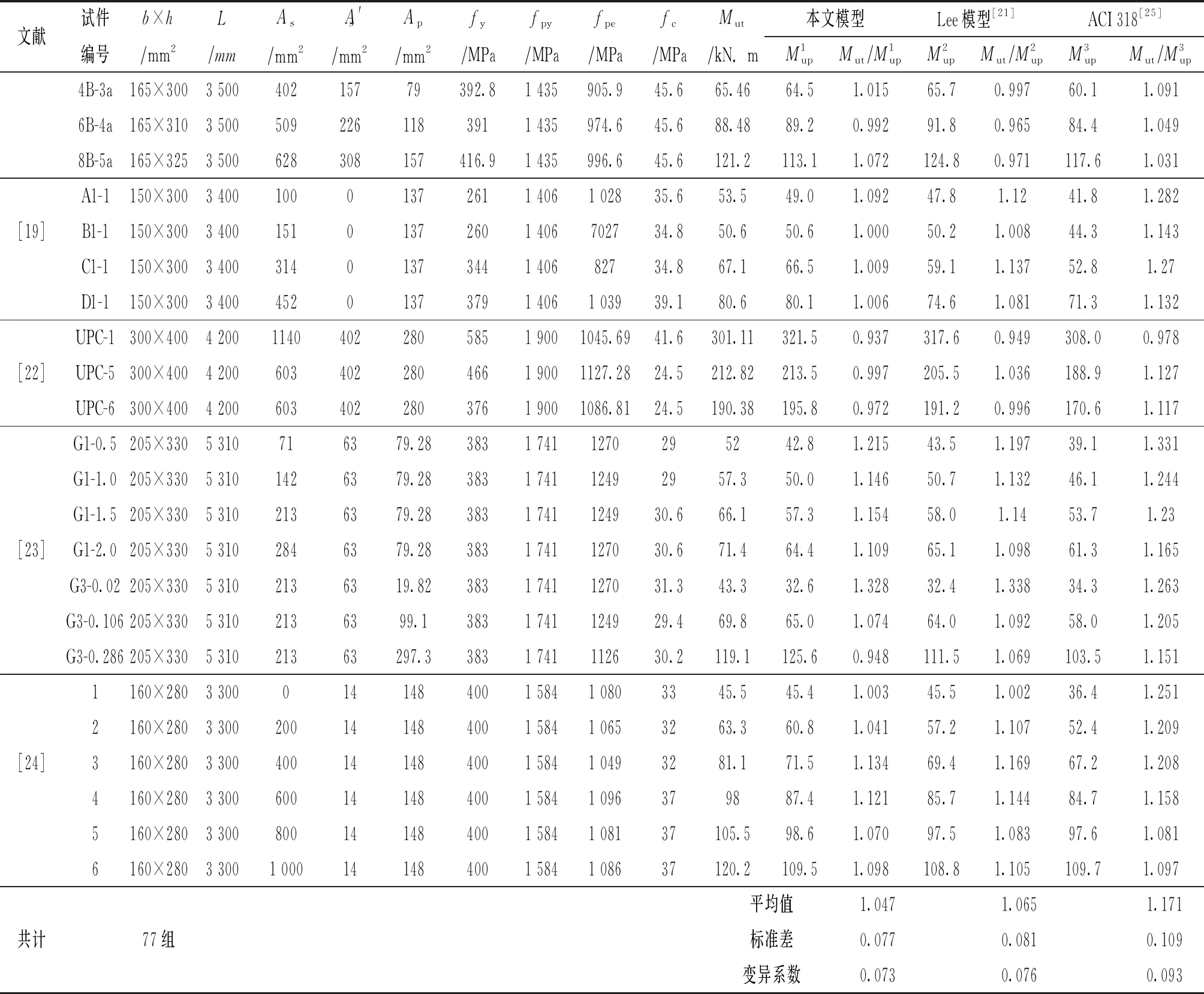
续表1
4 结论
(1)以两点对称荷载作用下无粘结预应力混凝土简支梁为研究对象,基于混凝土梁的整体变形及塑性铰分布特点,对预应力混凝土梁实际曲率分布进行简化后计算了预应力筋的应力增量,提出了无粘结预应力钢筋混凝土梁受弯承载力的计算方法;
(2)无粘结预应力混凝土梁抗弯承载力试验值与本文建议计算值之比的平均值为1.047,标准差为0.077,变异系数为0.073,吻合较好;
(3) 与其它计算模型的计算结果相比,本文建议计算模型较真实地反映了预应力混凝土梁的曲率分布;与ACI318规范的计算模型相比,可更准确的计算无粘结预应力混凝土梁的抗弯承载力,且本文分析方法有明确的物理力学模型.

