空气动力学距离对标枪运动员运动表现的影响：优秀女子标枪运动员吕会会投掷技术的个案研究

吕 钢 ，孙凯扬 ，买毅强 ，李翰君 ，刘 卉 ，于 冰

标枪投掷是田径运动中的4个投掷项目之一。由于标枪投掷成绩受空气的影响较大，对运动员的技术要求也较高。标枪投掷技术分为助跑、交叉步和最后用力3个阶段。其中，最后用力阶段以最后一次右脚落地为开始，标枪离手为结束。标枪投掷成绩由出手损失距离、真空飞行距离和空气动力学距离3部分组成（图1）。其中，出手损失距离是标枪出手点到落地点的水平距离中未被计入投掷成绩的部分；真空飞行距离是在不考虑空气作用的情况下，标枪按照抛物体运动模式计算的飞行距离；空气动力学距离是标枪实际飞行距离与真空飞行距离的差，是标枪受空气动力学因素影响增加或减少的飞行距离。

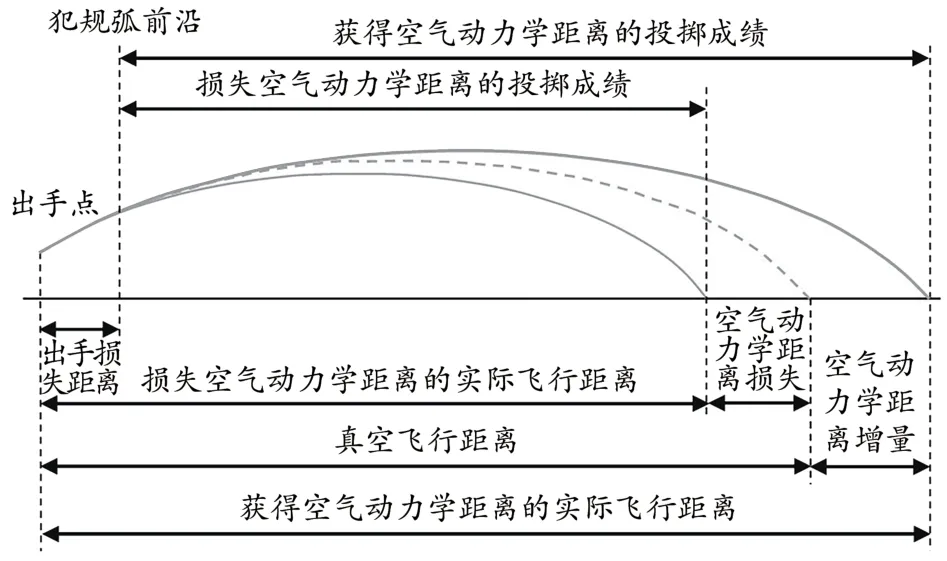
图1 真空飞行距离、空气动力学距离、出手损失距离、实际飞行距离和投掷成绩Figure 1.Vacuum Flight Distance，Aerodynamic Distance，Front Foot to Foul Line Distance，Actual Flight Distance and Throw Distance

力学理论和实验研究表明，出手速度是影响标枪成绩最重要的因素。在其他出手参数不变的情况下，出手速度越大，真空飞行距离越远，投掷成绩越好（王倩，2001；Hubbard，1984）。对优秀标枪运动员实际试投的生物力学研究表明，出手速度和投掷成绩呈显著正相关关系，说明出手速度是影响优秀标枪运动员投掷成绩的主要因素（Rich et al.，2008）。除出手速度外，出手角度和出手高度也是导致投掷成绩变化的主要原因（廖红等，2007；苑威威 等，2006；Bartlett et al.，1988；Best et al.，1987a）。

标枪投掷成绩还受到飞行中空气动力的影响。标枪飞行中受到的空气动力分解为垂直于标枪长轴的升力和平行于标枪长轴的阻力，其大小与标枪的攻角有关。标枪飞行中的俯仰角变化与标枪出手时的攻角和飞行中所受的空气动力对标枪产生的俯仰力矩有关。俯仰力矩使标枪围绕自身水平横轴旋转，其为正值时标枪向上旋转，枪尖向上抬起；为负值时标枪向下旋转，枪尖向下降落。Best等（1987b）通过对女子标枪的模拟计算发现，攻角为正值时，俯仰力矩均为负值，使标枪在飞行中向下旋转，缩短标枪飞行的空气动力学距离。Best等（1987b）、陶于等（2000）均发现女子标枪压力中心相对于质心的位置与攻角有关，使标枪向下旋转的俯仰力矩随着攻角的增大而增大（Schlichting et al.，1979）。这意味着运动员需要控制标枪出手时的攻角，控制标枪飞行中所受俯仰力矩初始值引起标枪向下旋转，增加空气动力学距离。Best等（1987b）提出，女子标枪运动中的最佳出手攻角为7°。

标枪的空气动力学距离还受到其飞行中自身振动的影响。由于最后用力过程中运动员对标枪的作用力方向不与纵轴平行，标枪出手时会产生振动。侧弯角是指由于运动员没有沿标枪纵轴用力，使标枪纵轴产生的弯曲角度。侧弯角越大，标枪飞行中的振动幅度越大。Bartlett等（1988）认为，标枪自身的振动会增大标枪受到的阻力，减小受到的升力。Hubbard等（1989）发现，在较小的攻角以及较大的相对风速下，标枪较大的振动幅度会使升力和阻力均有所提升，升力增加导致的飞行距离增加可能略大于阻力增加导致的飞行距离减小，即标枪的自身振动可能有利于提高投掷成绩。Hubbard等（1997）对标枪飞行中自身振动的进一步研究发现，标枪在俯仰平面内的振动会使飞行距离增加，左右方向上的振动则会使飞行距离降低。运动员出手时刻技术可能使得标枪的真空飞行距离和空气动力学距离相互制约，影响成绩。在给定的体能条件下，当运动员试图通过增加投掷的用力程度增加出手速度时，很可能造成出手时刻对速度方向和标枪姿位的控制失误，从而导致在增加标枪真空飞行距离的同时缩短了空气动力学距离，减小同时提高真空飞行距离和空气动力学距离的可能性，使其运动表现难以突破。

我国优秀女子标枪运动员吕会会在2018年虽然不断投出高水平的成绩，但一直徘徊在67 m以下，成绩没有突破性的提高。根据真空飞行距离、空气动力学距离和投掷成绩之间的关系，猜测吕会会的真空飞行距离与空气动力学距离存在某种相关，导致其运动表现受到限制，而真空飞行距离和空气动力学之间的相关与吕会会的技术特点有关。因此，本研究的目的：1）通过对吕会会2018年赛季投掷技术的生物力学分析，确定真空飞行距离与空气动力学距离之间的相关是否为限制她投掷成绩的因素；2）确定吕会会标枪出手时的攻角和侧弯角对空气动力学距离的影响；3）通过对吕会会2019年赛季的投掷技术分析验证2018年的分析结果。研究假设：1）吕会会的真空飞行距离与空气动力学距离负相关；2）真空飞行距离与空气动力学距离的负相关影响吕会会投出67 m以上成绩的概率；3）吕会会的空气动力学距离与其出手速度负相关；4）吕会会的空气动力学距离与其标枪出手时标枪的攻角和侧弯角相关；5）改进投掷技术动作（动作的形式和方向），降低真空飞行距离与空气动力学距离的负相关，可以提高吕会会投出67 m以上成绩的概率。

1 研究对象与方法

1.1 研究对象

研究对象为我国优秀女子标枪运动员吕会会，身高1.71 m，体质量70 kg，个人最好成绩为67.98 m（2019年7月12日国际田联世界田径锦标赛选拔赛），截止2020年3月31日，在国际田联世界排名第一。

1.2 研究过程

采集研究对象2018年4个全国比赛中的20次有效试投技术数据，分析其空气动力学距离与真空飞行距离的关系和这一关系对研究对象运动表现的影响，以及标枪攻角和侧弯角对研究对象空气动力学距离的影响。根据分析结果，于2019年冬季训练中指导研究对象对投掷技术进行改进。本研究在2019年春季第一次全国大型比赛中再次采集研究对象5次有效试投的生物力学数据进行分析，以验证之前的分析结果和训练效果。

1.3 数据采集

使用直接线性转换（direct linear transformation，DLT）三维录像技术获取研究对象在2018—2019年全国比赛中的技术录像，并运用两台分辨率为1 920×1 080 dpi的高清摄像机对研究对象每次试投的最后两步投掷技术进行拍摄。一台摄像机置于标枪助跑跑道的后方，另一台摄像机置于标枪助跑跑道的右侧，两台摄像机主光轴的夹角约为90°，拍摄频率为60幅/s，快门速度为1/1 200 s。每次比赛前在标枪跑道上设置4个悬挂立柱，将每个立柱上悬挂的一串6个小球作为标定点（图2），并测量4串小球在地面投影的中心间距。4串小球构成一个约长6.0 m×宽4.0 m×高2.5 m的标定空间，覆盖标枪投掷助跑最后一步和最后用力的空间（图2）。在标定空间的地面上设置5个地坐标标志点，用于建立大地坐标系。以大地坐标系为原点在投掷弧圆心的直角坐标系，X和Y轴平行于地面，正方向分别指向投掷方向和跑道的左侧；Z轴垂直于地面，正方向指向上方。完成对标定空间设置的拍摄后，移除所有标定设置，对研究对象的每次试投进行拍摄。

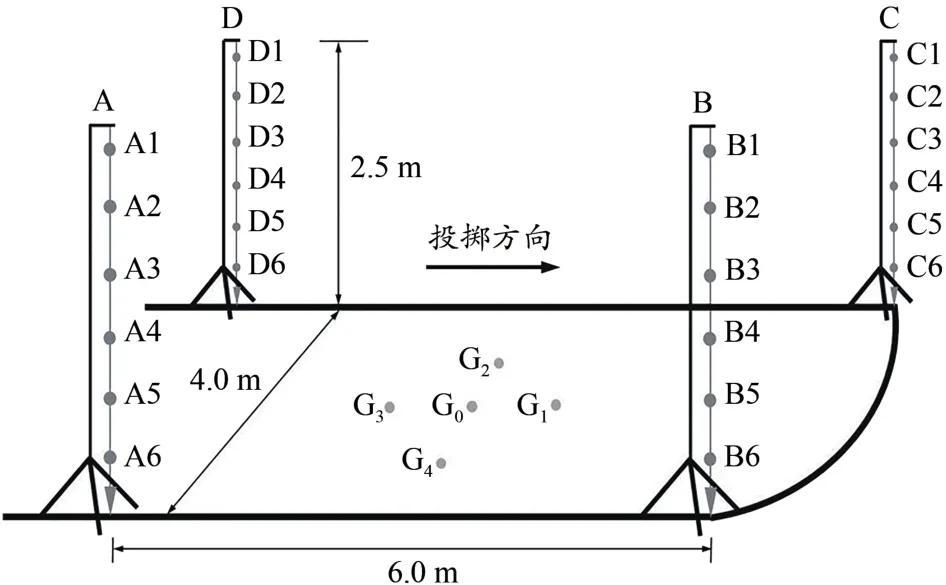
图2 标定空间和大地坐标系的设置Figure 2.Calibration Set--up for Data Collection

1.4 数据处理

使用人工智能自动数字化处理软件Fastmove Pose Creator数据标注版对标定设置画面和研究对象每次有效试投的视频进行数字化处理。对标定设置画面的数字化处理包括识别24个标定点和5个地坐标标志点的二维坐标。同时，截取研究对象每次有效试投的右脚最后一次落地前4幅画面到标枪出手后4幅画面，将剪辑后的2台摄像机录像视频导入Fastmove Pose Creator软件，自动逐幅识别21个人体关节点（Hay，1993）以及标枪线把前沿、标枪枪尖和标枪枪尾的二维坐标。应用Motionsoft 3D对2台摄像机进行标定计算并建立地坐标系，标定误差＜5 mm。利用研究对象右脚离地、左脚落地和标枪出手的关键画面，使用多幅同步技术对从2台摄像机中获得的二维坐标进行时间同步，消除每幅画面中扫描成像的时间 差（Dapena，1978；Hay et al.，1995；Leigh et al.，2008）。最后，使用DLT方法解算摄像机参数，计算人体21个关节点和标枪3个标志点在大地坐标系中的三维坐标。

1.5 数据计算

计算研究对象每次有效试投出手时的前后方向水平速度、左右方向水平速度、垂直速度、合速度、出手角度和出手高度，以及实际飞行距离和真空飞行距离。计算方法参考前人研究（刘生杰 等，2006；Best et al.，1987b；Hubbard et al.，1989）。标枪出手时的攻角定义为标枪枪尖和枪尾的连线与标枪出手合速度矢量之间在由标枪水平出手速度和垂直出手速度定义的垂直平面中的夹角（图3）。攻角为正值时，标枪枪尖在出手合速度矢量之上；攻角为负值时，标枪枪尖在出手合速度矢量之下。标枪出手时的侧弯角定义为标枪线把前沿到枪尖的矢量和枪尾到线把前沿的矢量之间在由标枪出手合速度矢量与大地坐标系Y轴定义的平面上的夹角（Hubbard et al.，1997）（图4）。

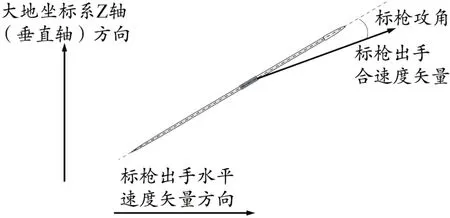
图3 标枪攻角Figure 3.The Javelin Angle of Attack

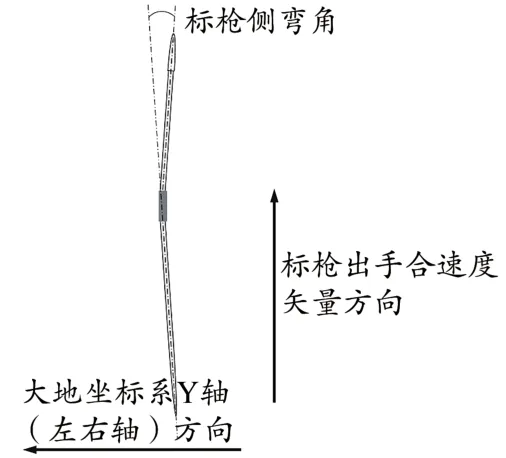
图4 标枪侧弯角Figure 4.The Javelin Side Bending Angle

本研究将标枪投掷成绩分为3部分：出手损失距离，真空飞行距离和空气动力学距离，表示为：

真空飞行距离和空气动力学距离之和为实际飞行距离，即标枪出手点到落地点的水平距离。这一距离可以根据标枪出手时线把前沿的水平位置、水平出手速度的方向、投掷成绩和犯规弧的半径，利用余弦函数计算获得。真空飞行距离根据抛物体运动学关系计算获得。在已知实际飞行距离和真空飞行距离的情况下，空气动力学距离为：

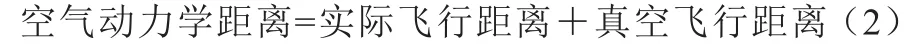
实际飞行距离和真空飞行距离的具体计算方法参考前人研究（Hay et al.，1995），已在多个研究中应用（赵爽等，2017；Leigh et al.，2007，2008，2010）。上述数据计算全部使用Javelin Throw 2016软件实现。

1.6 数据分析

为验证第1个研究假设，研究计算了研究对象在2018年全国比赛中20次试投的空气动力学距离与真空飞行距离的相关系数。为验证第2个假设，研究将运动表现量化为投掷成绩的概率，使用标枪投掷成绩的随机模型，通过蒙特卡洛模拟计算在给定空气动力学距离和真空飞行距离相关系数时，研究对象投出67 m以上成绩的概率（刘思伊等，2018；张美珍等，2016）。在标枪投掷成绩的随机模型中，标枪投掷成绩（do）表示为真空飞行距离（dv）、空气动力学距离（da）和出手损失距离（dl）的函数：

其中，dl设为常数，数值为2018年研究对象出手损失距离的平均值；dv假设为正态分布，平均值和标准差为2018年比赛中真空飞行距离的平均值和标准差。da表示为dv的回归函数。

其中，α、β1和β2为回归系数；ε为回归误差（高惠璇，2005；赵书祥，2005）。进行蒙特卡洛模拟时，dv根据分布状态随机取样获得；da通过回归方程表示为真空飞行距离函数，回归一个误差值平均为0，标准差等于回归标准差的正态分布，误差值根据分布状态随机取样获得。

进行标枪成绩的蒙特卡洛模拟计算时，可系统地改变da和dv之间的相关系数（R）值，再根据R值重新计算da和dv之间回归方程中的回归系数和回归标准差，根据新回归系数计算相对于每个随机采样dv的da值和投掷成绩。对每个给定R值进行100次模拟，获得研究对象取得67 m以上成绩的概率；重复5次改变R值的100次模拟，获得研究对象取得67 m以上成绩概率平均值和标准差。当研究对象投出某一距离以上成绩的平均概率大于0.167时，表明其平均每6次试投有1次超过这一成绩，即平均每次比赛成绩都超过这一成绩。本研究将这一成绩定义为研究对象的常态成绩。

为验证第3和第4个假设，研究计算了研究对象空气动力学距离与出手速度，以及空气动力学距离与标枪出手时攻角和侧弯角的相关系数。所有回归相关分析和随机模型的计算机模拟均使用Excel 2000软件实现。这些分析为研究对象2019年的冬季技术训练确定了方向。

为验证第5个假设，检验2019年冬季训练效果，本研究计算了研究对象2019年参加的第一个全国比赛中5次有效试投空气动力学距离和真空飞行距离的相关系数，以及投出给定成绩的概率，并与模拟结果进行比较。

2 研究结果

研究对象的空气动力学距离与真空飞行距离存在显著线性相关（R²=0.796 4，P=0.001）。

随机模型模拟结果显示，空气动力学与真空距离的相关关系影响研究对象投出67 m以上的概率（图5）。随着相关系数的降低，研究对象投出67 m以上成绩的概率增加。相关系数的平方降低到0.1时，研究对象投出67 m以上成绩的概率增加到17%。

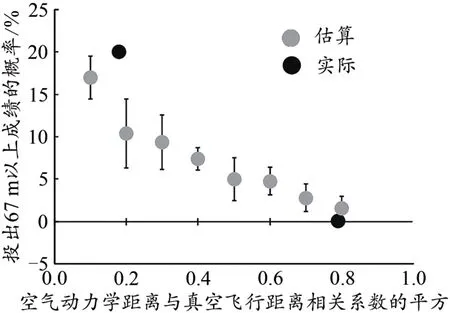
图5 空气动力学距离与真空飞行距离相关系数对投出67 m以上成绩概率的影响Figure 5.The Influence of the Correlation Coefficient between Aerodynamic Distance and Vacuum Flight Distance on the Probability of Throwing Distance over 67 m

研究对象的空气动力学距离与出手速度显著线性相关（R2=0.707 6，P=0.001；表1）。真空飞行距离与出手速度显著线性相关（R2=0.849 7，P=0.001），与出手角度和高度无显著相关（R2=0.012 1，P=0.644；R2=0.004 3，P=0.783）。空气动力学距离与标枪出手时的侧弯角显著负相关（R2=0.665 5，P=0.001），与攻角无显著相关（R2=0.043 8，P=0.353）。标枪出手时的侧弯角与出手速度显著线性相关（R2=0.730 2，P=0.001）。

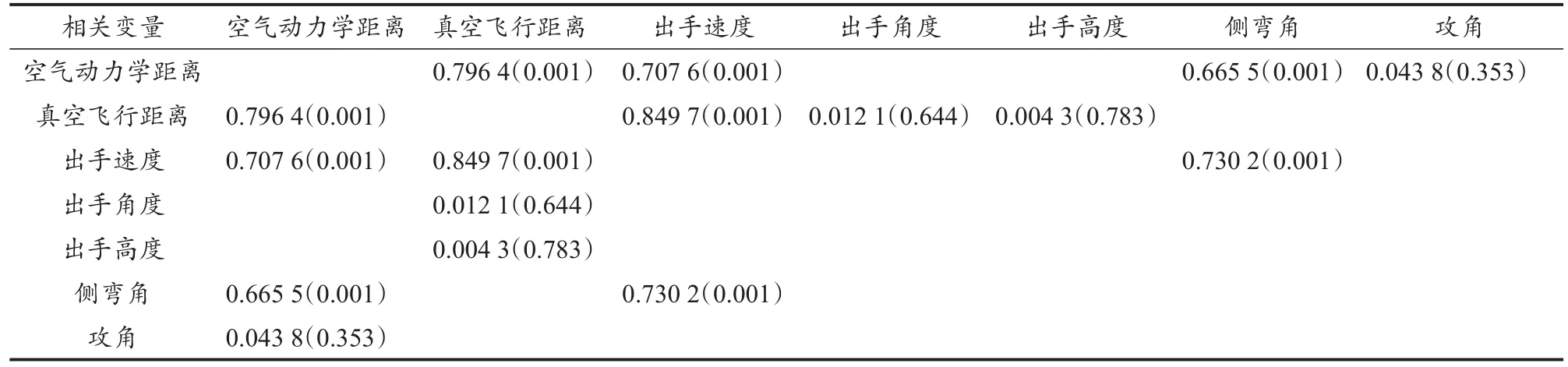
表1 空气动力学距离与真空飞行距离和技术参数相关系数的平方Table 1 The Square of the Correlation Coefficient between Aerodynamic Distance and Vacuum Flight Distance and Parameters

基于上述，在2019年冬季训练中着重改进研究对象标枪出手前的用力方向，强调向前用力，避免向左拉枪。技术改进后，研究对象在2019年冬季训练之后的第一次全国比赛中，5次试投的空气动力学距离与出手速度无显著相关（R2=0.080 9，P=0.897），投出一次67.72 m的成绩，超过67 m的比例为0.209。

3 分析与讨论

研究支持第1个研究假设：研究对象的空气动力学距离与真空飞行距离负相关；同时，支持第2个研究假设：空气动力学距离与真空飞行距离的负相关影响研究对象的运动表现。研究显示，研究对象在2018年全国比赛中的空气动力学距离与真空飞行距离显著负相关。生物力学随机模型模拟分析表明，空气动力学距离与真空飞行距离的负相关系数值越低，研究对象投出67 m以上成绩的概率越高。真空飞行距离和空气动力学距离是投掷成绩的主要组成部分。当空气动力学距离与真空飞行距离高度负相关时，真空飞行距离越长，空气动力学距离越短，限制了较长的真空飞行距离和与较长空气动力学距离组合的概率，限制了投掷成绩超过给定高水平成绩的概率。当真空飞行距离和空气动力学距离的变化范围一定时，两个变量相关系数值的降低使其相互影响程度降低，增加了较长的真空飞行距离和较长的空气动力学距离组合的概率，因而增加了投掷成绩超过给定高水平成绩的概率。

研究结果支持第3个研究假设：研究对象的空气动力学距离与她的出手速度相关。分析结果显示，研究对象的空气动力学距离与出手速度高度负相关，表明研究对象出手速度越高，获得的空气动力学距离越短。出手速度在一定程度上反映了研究对象投掷过程中用力的程度，说明研究对象的空气动力学距离与投掷中的用力程度有关，全力投掷时的空气动力学距离比没有全力投掷时短。

研究结果部分支持第4个假设：研究对象的空气动力学距离与出手时标枪的攻角和侧弯角相关。研究显示，研究对象的空气动力学距离与标枪出手时的攻角无显著相关，但与侧弯角显著负相关。这一负相关关系表明研究对象标枪出手时侧弯角越大，获得的空气动力学距离越短。在对标枪飞行中自身振动的进一步研究中，Hub‐bard等（1997）将标枪振动分为俯仰平面内的振动和左右方向上的振动，发现俯仰平面内的振动会增加标枪受到的升力，增加空气动力学距离，从而提高投掷成绩；左右方向上的振动会增加标枪受到的阻力，降低空气动力学距离，从而降低投掷距离。标枪出手时的侧弯是标枪飞行中左右振动的主要原因。与验证研究第3个假设相结合，表明研究对象投掷时用力越大，标枪出手时的侧弯角越大，飞行时自身的侧向振动越大。赵爽等（2017）发现，与世界优秀运动员相比，我国女子标枪运动员出手时的侧向速度较大，这一发现与本研究结果一致。

研究对象标枪出手时侧弯角和出手速度的相关系数与其技术特点有关，使用了大幅度身体绕纵轴旋转的投掷技术。这一技术有利于增加出手速度，但对于右手投枪的运动员容易出现围绕纵轴向左旋转过度的情况，造成向左拉枪，加大标枪出手时的侧弯角，因而增加标枪飞行中的左右振动，不利于获得空气动力学距离。在2019年冬季训练中，加强对研究对象最后用力先前性的训练，强调最后用力的最后阶段右肩向前运动，避免过度向左旋转，减小向左拉枪。

研究结果支持第5个研究假设：通过改进技术降低空气动力学距离与真空飞行距离的负相关将提高研究对象的运动表现。研究表明，2019年第一次全国比赛中，研究对象的空气动力学距离与真空飞行距离的相关明显降低，并以67.12 m的成绩打破亚洲女子标枪记录，投出67 m以上成绩的实际比例为20%。这与本研究随机模型模拟的结果一致。

本研究是对优秀运动员的个案研究，研究结果不一定适用于其他运动员。运动员的技术特点不同，影响空气动力学距离的技术因素也不同。由于影响不同运动员空气动力学距离的技术因素不同，运动员的体能条件不同，大样本横向研究很难确定影响空气动力学的技术因素。虽然个案纵向研究的样本量相对大样本横向研究较小，但是体能和技术水平等因素可以控制，因而更容易发现技术因素对成绩的影响，结果的可靠性和实用性更高。

4 研究结论

1）真空飞行距离与空气动力学距离的负相关是限制标枪投掷运动表现的因素之一；2）减小真空飞行距离与空气动力学之间的负相关能增加高水平标枪投掷概率；3）全力投掷中向左拉枪增加标枪出手时的侧弯角和飞行中的侧向震动，会增加真空飞行距离和空气动力学距离的相关系数，从而影响标枪投掷成绩。