基于时效差的山洪预警评定方法

张艳军，邹薏轩，王协康，张平仓，许文盛

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；2.四川大学水力学与山区河流开发保护国家重点实验室，四川成都 610065；3.长江水利委员会长江科学院，湖北武汉 430010)

山洪灾害是由山丘区强降雨引发的陡涨陡落洪水，并伴随洪水引发的泥石流、滑坡等的灾害，常造成人员伤亡、经济损失并影响社会安全[1]。据统计，21世纪以来，中国每年因山洪灾害死亡人数约1000人，占洪涝灾害死亡人数的70%左右[2]。山洪灾害已成为当前防洪减灾工作中的重点，而构建监测预警体系，增强监测预警能力，是提升防灾减灾救灾能力的关键[3]。有效的洪水评定方法可优选水文模型，从而提高山洪预警的精度和响应时间，减少山洪灾害的损失[4]。

目前，常用的洪水预报评定指标主要基于数理统计指标，包括绝对误差、相对误差、均方误差和纳什效率系数等。例如张娟等[5]选用洪量相对误差、洪峰相对误差、峰滞时间和纳什效率系数4个指标开展校正效果评估，以提升洪水预报精度，延长洪水预报有效预见期。黄艳等[6]选用相对误差、合格率等指标比较了不同水文模型在山洪预报中的模拟效果，认为半分布式模型比集总式模型有较大优势。李爽[7]为提高北方旱区中小河流洪水预报精度，采用确定性系数、径流相对误差、洪峰误差和峰现时间误差4个指标论证模型的可靠性。王璐等[8]将5种常用的水文模型应用于湿润、半干旱半湿润地区的14个典型山区小流域，选用平均相对误差、确定性系数等指标，认为API、新安江、TOPMODEL模型在湿润地区模拟效果较好，HEC-HMS模型在湿润地区、半湿润半干旱地区适用性最强。Chen等[9]以均方根误差和平均相对误差为评定指标，探讨了结合粒子滤波同化模型与一维水动力模型在黄河下游微模型水位变化的应用。Kurian等[10]以纳什效率系数为评定指标，评定了一种结合分布式水文模型和数据驱动模型的混合模型M4，认为该模型对提前生成预报流量效果良好。

在应用水文模型时，受复杂水文过程和实测数据质量的影响，尤其是水文模型的物理基础与山区小流域实际产汇流机制仍存在一定差异，造成模型在山洪预警时易出现虚警和漏警现象。虚警和漏警这两个概念源于信息化领域，虚警是错误的告警事件，即当没有目标时，系统却对非目标事件进行告警[11]；漏警是检测系统在检测时就可能把某些入侵行为错判为正常行为，或者就根本检测不到这一入侵行为[12]。在山洪预警中，将实际不需要预警但是模型发出预警的情况称为虚警，一般发生于预报的洪量比实际发生的洪量偏高或峰现时间偏早的情况。虚警可能造成不必要的人员转移及经济财产损失。将实际需要预警，但模型未预警的情况称为漏警，一般发生于预报的洪量比实际发生的洪量偏低或峰现时间偏晚的情况。漏警可能造成巨大的经济财产损失，甚至是人员伤亡。在使用绝对误差、相对误差、均方误差和纳什效率系数等数理统计方法的精度评定模型中，由于同等对待真值两侧的误差，在理论上，虚警和漏警会以相同的概率出现。

山洪预警实践中，考虑虚警和漏警导致的经济财产损失和人员伤亡差异，若模型模拟洪峰比实际洪峰高、或预警时刻出现在实际预警时刻之前，对于防洪减灾效果来讲，则认为更安全，即虚警较漏警更容易接受。然而，常用的洪水预报评定指标一般着重考虑模型模拟结果与实际的数量偏差，较少涉及山洪的虚警和漏警问题。

为此，作者以基于山区小流域暴雨山洪水位上涨变化的水位预警方法为基础，考虑“优先减少漏警”的山洪预警原则，提出“山洪预警时效差”作为山洪预警评定方法，并比较分析了TOPMODEL模型、TVGM模型和新安江模型在官山河流域较大洪水的预警效果。

1 流域概况

官山河流域处于湖北省十堰市丹江口市西南部，地处东经110°42′30″～111°00′22″，北纬32°16′19″～32°32′15″，属汉江中上游干流的右岸支流，发源地是湖北省十堰市房县，主要支流为袁家河和吕家河，地理位置如图1所示。干流河道平均坡降为0.57%，流域面积为465 km2，多年平均流量为7.78 m3/s；地形以丘陵、中小型起伏山地为主，中部地势较低，边缘地势较高，海拔为153～1634 m，平均高程为690 m[6]。

官山河流域位于鄂豫暴雨区，该地局地性暴雨频发，属于连阴雨高发地区，也是山洪灾害、泥石流灾害和滑坡灾害多发的地区。据统计，1975年以来官山河流域共发生12次山洪灾害。2012年“8·5”超百年一遇特大洪水是历年最严重的一次山洪灾害，造成镇区交通、通讯、电力、供水全部中断，波及官亭、骆马沟、五龙庄等9个村，损坏房屋2 492间，冲毁公路160 km、桥梁29座，受灾农田约9100亩，转移人口约7000人，死亡3人，造成直接经济损失2.3亿元[13]。

图1 官山河流域地理位置图Fig.1 Administrative division map of Guanshanhe basin

本文所使用的官山河的水文数据来源于官山河下游的孤山水文站，站点位置见图2。从1975年以来的水文年鉴中摘录和整理各场次洪水过程。

图2 官山河流域站点位置图Fig.2 Sketch map of hydrological station at Guanshanhe basin

2 研究方法

2.1 水文模型

1）TOPMODEL模型

TOPMODEL模型是基于地形的有一定物理机制的半分布式水文模型，其利用地形指数ln（a/tan β）或地形-土壤指数ln（a/T tan β）（a为单位等高线长度的排水面积、tan β为地表坡度、T为导水系数）来反映流域水文现象，尤其是径流运动的分布规律，可以用于模拟湿润山区小流域的洪水过程[14]。

2）TVGM模型

TVGM模型由武汉大学夏军教授提出，其产流理论基础是基于降雨-径流非线性关系，汇流采用了简单的响应函数模型，通过考虑土壤湿度，引入时变增益的概念，使用简单的产、汇流方程构建模型，避免了Volterra泛函级数辨识困难问题，从而使得较为复杂的基于Volterra泛函级数的水文非线性系统能够以一种较为简单的概念模型进行表达，也比较适合模拟湿润山区小流域的洪水过程[15-16]。

3）新安江模型

新安江模型始建于1973年，最早由河海大学赵人俊教授提出，并改进发展成为三水源以及其他多水源的模型[17-18]。该模型多应用于湿润地区与半湿润地区的水文预报和水文设计，主要包括4部分：蒸散发计算、产流计算、水源划分以及汇流计算。新安江模型是我国湿润地区最常使用的水文模型。

2.2 预警方法

目前，在山洪预警预报方法上，国内外常用的山洪预警预报方法有山洪临界雨量法、山洪预报模型与方法和经验预报法等[19]。叶金印等[20]以新安江模型为基础，提出了考虑土壤含水量饱和度的动态临界雨量山洪预警方法，山洪预警合格率超过了70%；孔凡哲等[21]提出了一种考虑雨强时间分配的临界雨量计算方法，在裴河流域，选取适用的雨强时间分配模式，得到临界雨量，使山洪灾害预警的成功率由均匀分配方法得到的12%提高到50%，漏报率由88%降低至50%；刘姝熠[22]对HEC-RAS的研究表明，其洪水淹没模拟分析具有较高的准确性和可靠度，可为辽河流域洪水预警以及洪水灾害人员疏散方案的制定提供一定的参考；Dao等[23]研究了城市洪水预警的诱发降雨和径流，结果表明，不考虑降雨时间变化的预警系统的错误预警大约是考虑降雨时间变化的预警系统的两倍；Yuan等[24]用特征降雨和层次分析法对灾害预警时间的合理性判别因子和权重进行了评价，确定了综合合理性指数（CRI），并对防灾对象临界雨量的总体合理性进行了评价和复核。

除此之外，2019年，王协康等[25-26]提出一种新的山洪预警办法——基于山区小流域暴雨山洪水位上涨变化的水位预警方法，该方法根据洪水水位上涨率的变化情况判断是否准备转移或立即转移，比较适合官山河这种坡度较大，水位陡涨陡落的山区小流域。该方法的实施具体如下：

1）当洪水水位上涨率一旦达到1 m/h时，立即发出准备转移预警。

2）在洪水水位上涨率达到1 m/h之后的10～30 min，连续进行n次洪水水位上涨率测量，记作α11，α12，···，α1n。

若α11,α12,···,α1n均≥1，说明洪水发展到了洪水水位陡涨阶段。根据式（1）计算洪水水位达到成灾水位的预计时长t；根据式（2）计算洪水水位达到成灾水位的预计时刻 T1，在 T0～（ T1-t0）时间段内尽早发出立即转移预警，其中， t0为防灾对象所在地区的最小预警时段，一般取0.5 h。

若 α1n＜1，则按照式（3）估算洪水水位达到成灾水位的预计时长t，若洪水水位达到成灾水位的预计时长t处于（30 min，60 min]时间区间，则立即发出立即转移预警；若洪水水位达到成灾水位的预计时长t＞60 min，则不用发出立即转移预警，继续监测目标河段的洪水水位上涨率。

式（1）～（3）中： t为洪水水位达到成灾水位的预计时长； Z0为成灾水位； Z1为准备转移水位，准备转移水位是指洪水水位陡涨阶段的初始水位，洪水水位陡涨阶段是指洪水水位上涨率始终≥1 m/h的阶段。 α1为α11,α12,···,α1n中的最大值， T1为洪水水位达到成灾水位的预计时刻， T0为洪水水位陡涨阶段起始时刻，α2为α11,α12,···,α1n中的最小值；

3）在继续监测目标河段的洪水水位上涨率的过程中，若洪水水位上涨率又达到1 m/h，重复步骤2），直到洪水消退[25-26]。

以这种方法为基础构建山洪预警时效差。

2.3 传统评定指标[4]

1）洪峰流量相对误差

模拟洪峰流量减去实测洪峰流量为洪峰流量预报误差，洪峰流量预报误差除以实测洪峰流量为洪峰流量绝对误差，以百分数表示。

2）峰现时间绝对误差

峰现时间的模拟值减去实测值的绝对值为峰现时间绝对误差。

3）纳什效率系数

洪水预报过程与实测之间的吻合程度可以用纳什效率系数为指标[4]，计算公式如下：

2.4 山洪预警时效差

根据王协康等[25-26]提出的基于山区小流域暴雨山洪水位上涨变化的水位预警方法，本文提出立即转移预警时效差（ΔTr）、准备转移预警时效差（ ΔTp）和成灾水位出现时效差（ΔTd）等3个考虑预警效果的指标。在山洪预警时，立即转移预警时效差最为重要，准备转移预警时效差次之，成灾水位出现时效差最末，而山洪预警时效差综合考虑了这3个指标的影响：

式中： ΔT 为山洪预警时效差，h；Δ TR、 ΔTP、 ΔTD分别为 ΔTr、 ΔTp、Δ Td的函数值（见式（7）、（9）、（11））； ω1、ω2、 ω3分别为立即转移预警时效差、准备转移预警时效差和成灾水位出现时效差这3个指标的影响因子，可由层次分析法[27-28]分析得到。

由定义可知，山洪预警时效差 ΔT 为非负数，数值越小，表明模型的山洪预警结果与实际情况相差越小，模型用于洪水预警的预警效果越好；数值越大，表明模型的山洪预警结果与实际情况相差越大，模型用于洪水预警的预警效果越差。

与山洪预警时效差相关的3个指标及其函数值定义如下：

1）立即转移预警时效差

式中： Tr实为根据实测流量计算得到的立即转移预警时刻； Tr模为由水文模型模拟流量计算得到的立即转移预警时刻； ΔTr为两个时刻的差值； Tr模比 Tr实早为正，晚为负，h。

一般来说，根据水文模型计算得到的立即转移预警时刻早于由实测流量计算得到的立即转移预警时刻较好。所以，当ΔTr小于0时，应使用系数 m1放大其误差， m1＞1。

2）准备转移预警时效差

式中：Tp实为由实测流量计算得到的准备转移预警时刻；Tp模为由水文模型的模拟流量算得的准备转移预警时刻；ΔTp为两个时刻的差值， Tp模比Tp实早为正，晚为负，h。

同理，当Δ Tp小于0时，应使用系数 m2放大其误差，m2＞1。

3）成灾水位出现时效差

式中：Td实为由实测流量算得的成灾水位出现时刻；Td模为由模型模拟流量算得的成灾水位出现时刻；ΔTd为两个时刻的差值， Td模比Td实早为正，晚为负，h。

同理，当Δ Td小于0时，应使用系数 m3放大其误差，m3＞1。

在式（7）、（9）、（11）中，m1,m2,m3为人们在立即转移预警时刻、准备转移预警时刻和成灾水位出现时刻等3个时间点对虚警的接受程度与对漏警的接受程度的比值。考虑到这三者在山洪实践中都是反映虚警和漏警造成损失的差别；在数学计算上，都是反映“计算值早于真值”与“计算值晚于真值”在评判计算结果时的权重的差异。因此，本文假设三者相等，即 m1=m2=m3，在计算时，都用 m表示。

2.5 层次分析法

层次分析法适用于分析解决一些结构比较复杂、难以量化的多目标决策问题[28]。主要步骤如下。

1）建立判断矩阵[27-28]

aij值表示要素i与要素 j的重要性比较结果，影响要素两两比较时，确定了 aij值的9级标度见下表1，且主对角线数字 aij=1，且 aji=1/ aij，由此建立判断矩阵。

表1 aij的9级标度Tab.1 9-level scale of a ijvalue

2）求判断矩阵特征向量[27-28]

在计算影响因子 ω1、 ω2、 ω3时， a1为立即转移时效差， a2为准备转移时效差， a3为成灾水位出现时效差。对山洪预警来说，立即转移时效差最为重要，因为山洪灾害即将发生或有非常高的概率发生，能否准确预警立即转移时刻，直接关系到人民生命安全能否得到有效保障[3]。准备转移时效差的重要性次于立即转移时效，当检测到实时雨情水情达到系统预先设定预警指标时，能否准确预警准备转移时刻，关系到人群是否已经做好准备，能否成功及时转移[3]。成灾水位时效差重要性最低，因为若能及时发布准备转移预警和立即转移预警，由于成灾水位出现时，人群已经及时转移，不会造成太大的影响。据此重要性排序，认为 a1较 a2介 于略微与明显重要之间， a1较 a3绝对重要， a2较 a3介 于明显与十分明显重要之间，即 a12=4，a13= 9， a23=6，建立的判断矩阵如下：

计算特征向量得到，影响因子 ω1= 0.69， ω2= 0.25，ω3= 0.06。

在计算人们对虚警的接受程度与对漏警的接受程度的比值 m时， a1为虚警， a2为漏警，考虑到在山洪防治实践中漏警威胁远大于虚警，且漏警很可能会造成人员伤亡，可以认为 a1较 a2绝对重要，即 a12=9，建立判断矩阵如下：

计算特征向量得到， ω1=0.9， ω2=0.1，则 m=ω1/ω2= 9。

以官山河2012年的8·5洪水为例，此次官山河死亡3人，造成直接经济损失2.3亿元[13]。若提前转移7000人，虽然直接经济损失仍难以避免，但可以避免人员死亡。若该山洪预警为虚警，假设该地区每人每天的收入为i元，即转移造成的直接经济损失为转移当天的收入，即7000 i元。若不进行山洪预警，即发生漏警，在房屋和农田淹没损失之外，将额外损失3条生命，参照交通事故死亡赔偿标准，仅仅计算死亡赔偿金，即每人20年收入，其额外的经济损失为21900i元。因此，可以计算得到损失比例约为1∶3，即 m=3。但是，由于未计算交通事故还需考虑的处理事故费用、被抚养人生活费和精神损害抚慰金，也未计量人的生命价值，因此该 m远远偏小。综合该实例与层次分析法的结果，取 m= 9。

3 计算结果

3.1 传统评定方法的评定结果

收集官山河流域自1975年以来8场较大的洪水，将1975至1983年的5场水作为率定场次，将1983年至2015年的3场水作为验证场次。使用洪峰流量相对误差、峰现时间绝对误差和纳什效率系数等3个传统指标，对TOPMODEL模型、TVGM模型和新安江模型分别进行评定。评定的结果见表2和图3。从洪峰流量相对误差来看，TVGM模型最优，TOPMODEL模型次之，新安江模型较差；从峰现时间绝对误差来看，新安江模型最优，TVGM次之，TOPMODEL较差；从纳什效率系数来看，TVGM模型最优，TOPMODEL模型次之，新安江模型最差。综合这3个传统指标综合来看，TVGM模型最优，更适合官山河流域的洪水模拟。

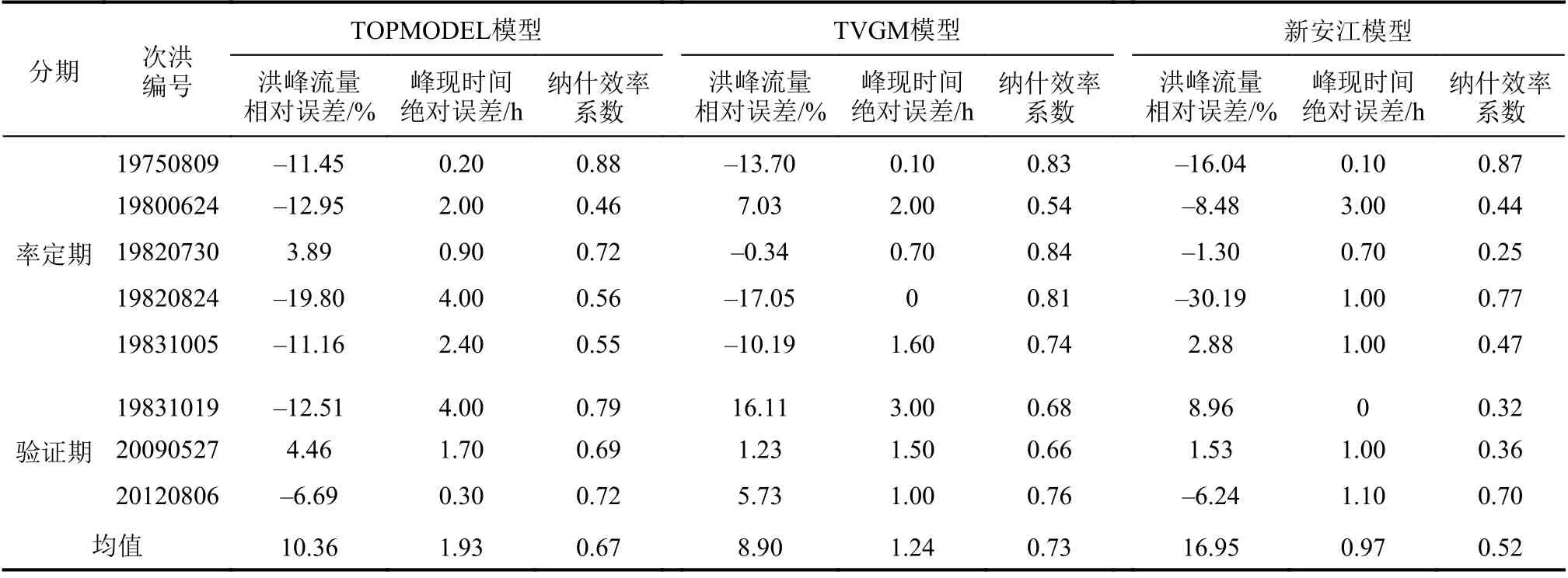
表2 官山河流域8场较大洪水模拟结果比较Tab.2 Comparison of 8 large floodssimulation resultsat Guanshanhe basin

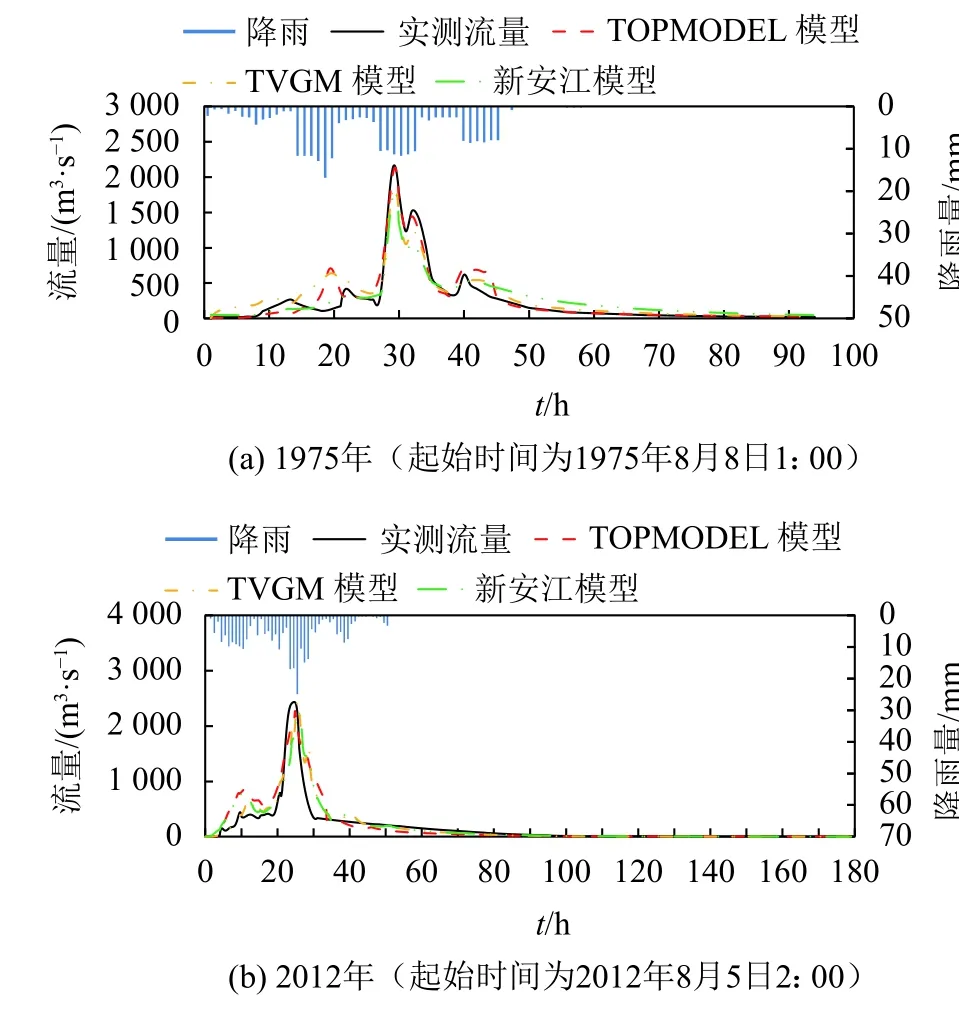
图3 洪水模拟过程线Fig.3 Simulation process hydrographs

3.2 山洪预警时效差的评定结果

官山河流域的成灾水位根据历年山洪灾害出现频次及受灾程度，取20年一遇的设计洪水的洪峰流量对应的水位，即32.38 m。

基于传统评定标准的模型评定结果并未直接针对洪水预警，因此有必要评定其山洪预警时效差。将实测值和3个模型的模拟值插值为时间间隔为6 min的时间序列，进行预警并计算洪水处置时效（Δ T），结果见表3。从表3可知，次洪编号为19800624、19820824和19831019的3场洪水的水位未达到成灾水位，且不需要发出准备转移预警；次洪编号为19820730、19831005和20090527的3场洪水虽需要发出准备转移预警，但不需发出立即转移预警且未达到成灾水位；而1975年和2012年出现特大洪水，且这两场洪水水位达到成灾水位，需要发出准备转移预警和立即转移预警。

为了进一步比较洪水处置时效与传统评定指标在山洪预警方面的评定效果，将山洪预警时效差的计算结果绘制成图，如图4、5所示。

从表3及图4、5的官山河1975年和2012年山洪预警结果可以看出，TOPMODEL模型的山洪预警时效差 ΔT ＜TVGM模型的山洪预警时效差 ΔT＜新安江模型的山洪预警时效差 ΔT，即TOPMODEL的预警效果最好，TVGM模型次之，新安江模型最差。具体情况如下：1）对于新安江模型，1975年和2012年的立即转移预警和成灾水位出现时刻均在实际预警时刻之后，表明在两场特大洪水中均出现了漏警现象，尽管时间相差不久，但对于山洪来说，也会造成巨大的经济财产损失，甚至会造成人员伤亡，不符合山洪预警原则。2）对于TVGM模型，虽然1975年预警的立即转移时刻与实际预警时刻相同，且预警的准备转移时刻与实际相差较小，但预警的准备转移时刻和成灾水位出现时刻皆在实际预警时刻之后，而2012年准备转移预警时刻也在实际预警时刻之后。这两场洪水的预警中都出现了漏警现象，不利于山洪灾害处置。3）对于TOPMODEL模型，1975年的准备转移预警和立即转移预警时刻虽然与实际预警时刻相差最多，但都在实际预警时刻之前，并未出现漏警，而2012年的TOPMODEL模型虽然在预警准备转移时刻时出现了漏警，但相对其他两个模型，漏警程度最轻。综上所述，TOPMODEL模型更符合山洪预警的要求，从山洪预警时效差的评定结果来看，也是TOPMODEL模型最优。

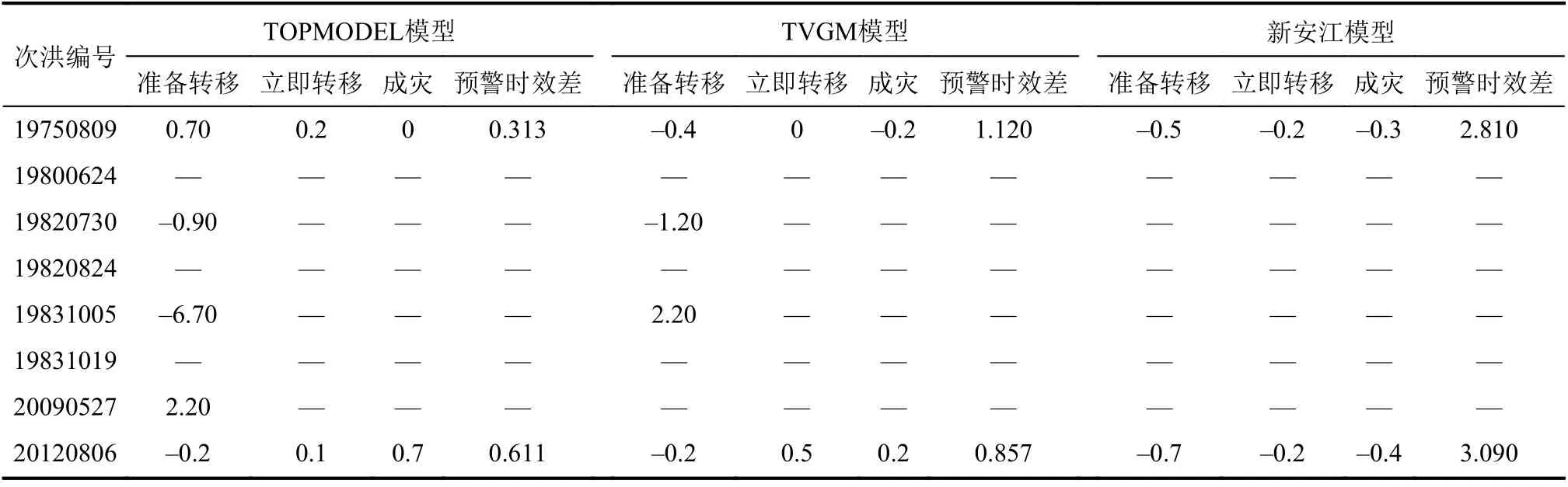
表3 官山河流域8场较大洪水各模型的预警时效差Tab.3 Comparison of the temporal difference of 8 large floods warning results at Guanshanhe basin

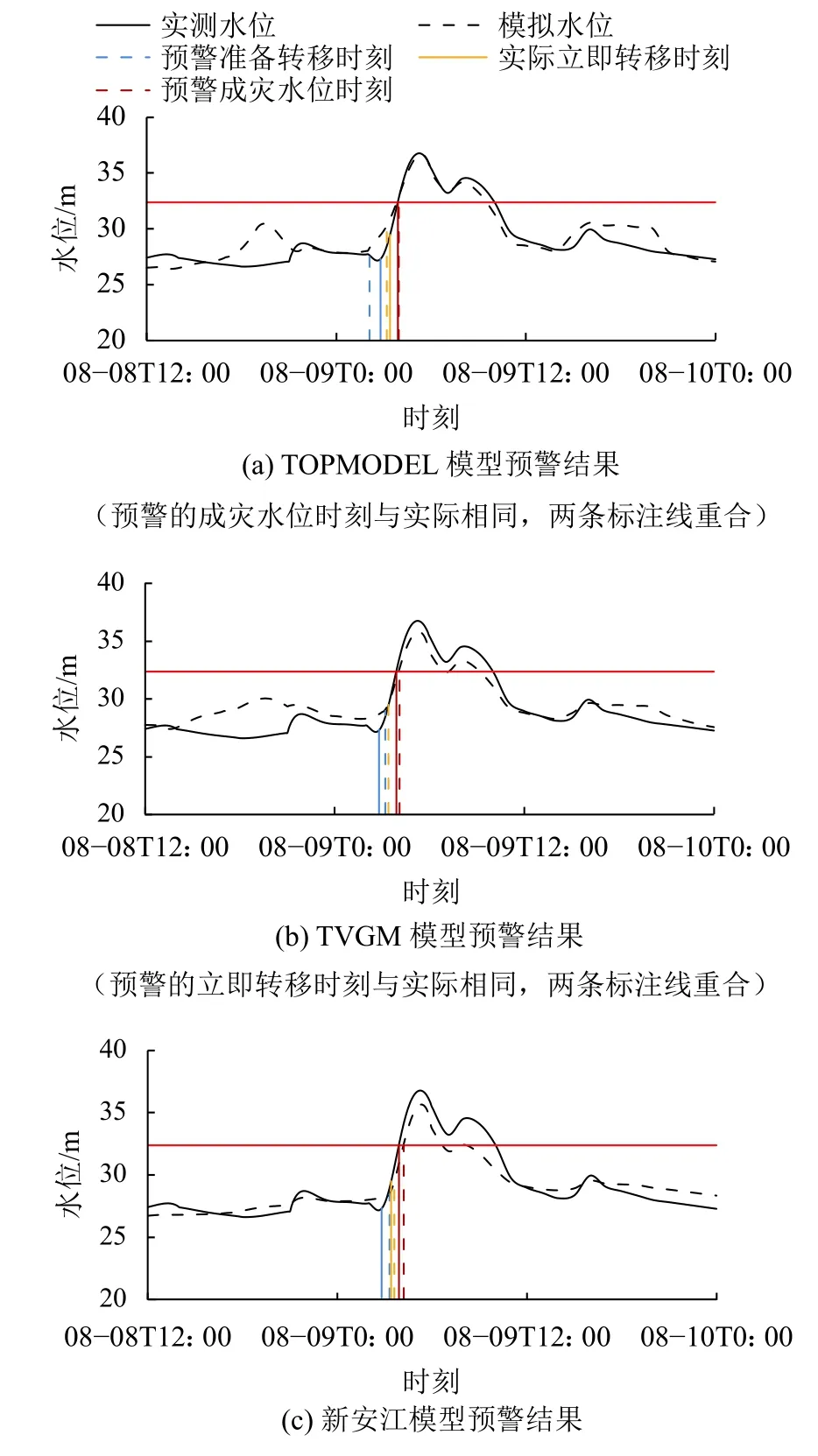
图4 官山河1975年山洪预警结果Fig.4 Warning result of Guanshanhe basin in 1975

图5 官山河2012年山洪预警结果Fig.5 Warning result of Guanshanhe basin in 2012

3.3 评定结果比较

造成传统评定指标的评定结果与洪水处置时效评定结果不同的原因，是因为传统评定指标认为虚警和漏警是同等不利的，无论是计算值大于真值，还是计算值小于真值，都应该同等赋权优化。而山洪预警时效差根据山区小流域暴雨山洪的漏警威胁大于虚警的山洪防治实践，认为应优先减少漏警。通过比较分析，若按照传统评定指标的评判结果，认为TVGM模型最优，但在用TVGM模型进行山洪预警时，会出现漏警现象，很可能会造成巨大的经济财产损失和人员伤亡。若用山洪预警时效差来评定预警效果而选出的最优模型——TOPMODEL模型，则可以有效避免漏警，更符合山洪防治的实践需求。

4 结论与讨论

1）根据山区小流域暴雨山洪的漏警威胁大于虚警的山洪防治实践，和“优先减少漏警”的原则，提出了一个衡量山洪预警效果的指标——山洪预警时效差，该指标为非负数，数值越小，山洪预警结果与实际情况相差越小，模型用于洪水预警的预警效果越好；数值越大，山洪预警结果与实际情况相差越大，模型用于洪水预警的预警效果越差。

2）选用洪峰流量相对误差、峰现时间绝对误差和纳什效率系数3个传统评定指标，来评定TOPMODEL模型、TVGM模型和新安江模型对官山河流域8场较大洪水的预警效果。通过传统的评定指标，认为TVGM模型最优。

3）选用山洪预警时效差对模型进行评定，则认为TOPMODEL模型最优。造成两个结果不同的原因是，传统评定指标认为山洪的虚警和漏警是同等不利的，而山洪预警时效差认为虚警和漏警对山洪防御的影响并非相同，应优先减小漏警的可能性。因此，传统评定指标选出的模型可能会造成更多的漏警现象，而“山洪预警时效差”可以有效减少漏警的问题，即用“山洪预警时效差”来评定山洪预警效果较好。

4）只检验了该指标对于TOPMODEL模型、TVGM模型和新安江模型3种模型用于官山河流域较大洪水的模拟和预警的效果，若要进一步评价该指标，可以将该指标推广于其他山区流域和其他水文模型。同时，该指标也可以引用更多的预警方法来评定预警效果。

5）官山河流域的成灾水位是根据历年山洪灾害出现频次及受灾程度，取20年一遇的设计洪水的洪峰流量对应的水位。但在实际情况中，成灾水位受到前期降雨影响很大，成灾水位与设计洪水频率可能并不一致，因此在后续研究中将加强对成灾水位与设计洪水频率关系的研究。

6）准备转移预警、立即转移预警主要取决于洪水水位上涨率。根据已有研究成果[25-26]，判定洪水水位上涨率的指标是1 m/h，但在不同的山区河流，情况复杂多变，该值可能有变化，应具体分析。因此，在后续研究中，需针对不同山区河流分析该指标的合理取值。