基于数据驱动的变风量空调 AHU 故障诊断研究
庞义旭 鹿世化 陈玮玮 田建新
1 南京师范大学能源与机械工程学院
2 吴江炀明空调净化有限公司
0 引言
变风量空调系统一般由空气处理机组(AHU,A ir Handling Unit),风管系统,自动控制系统和末端装置4个部分组成,因具有节能和舒适性的优点[1],受到了广泛的应用。但是,在操作过程中,控制元件不可避免地容易出现各种异常故障[2]。此类故障最终反映为能源效率下降,从而造成不必要的能源浪费[3-5]。因此对AHU 系统的故障检测研究具有重要价值及意义。
本文以某工厂变风量空调实验室为研究对象,首先收集AHU正常运行时的监测数据,经过滤波处理后,再利用标准化数据集 PCA建模,确定Q统计量[6-8]的阈值δ2,根据阈值SPE 统计量和阈值δ2的大小来确定AHU 的故障检测率,然后通过比较BP 神经网络算法[9]和Q贡献率图法对系统故障诊断诊断率,找出故障的具体来源,进而确定最佳系统故障诊断方案。
1 数据采集
研究对象是某工厂变风量空调实验室,原理图如图1 所示。AHU 中分布着新风温湿度传感器,混合风温湿度传感器,回风温湿度传感器和回风温湿度传感器,系统通过控制冷冻水阀门来控制送风温度,通过房间负荷来控制变频风机的送风频率。传感器及阀门信号数据每1 min 记录一次,通过MODBUS 协议传输到PLC 中,PLC 再通过物联网平台实时传送到云端。

图1 变风量空调系统原理图
为了能够全面的描述 AHU 的运行特性,从能量守恒和质量守恒出发,如图 2 所示,本文选取送风温度Ts、新风温度To、混合风温度TM、回风温度Tr、供水温度Tws、回水温度Twr、冷冻水流量Was、回风湿度Dr、送风量Mas这9 个变量为PCA 模型的原始数据集。实验从早晨 6 点开始,一直持续运行到 18 点,数据每 1 min 传输一次,去除无效数据后,总共采集到720 组数据。

图2 AHU 能量交换原理图
2 模型建立及数据分析
2.1 PCA 模型建立
AHU 机组正常运行时常常处于动态变化中,系统总会受到干扰作用,会使数据有噪声的存在,而因外界干扰而产生的数据集质量如果不高就会对模型的准确性带来很大的挑战。因此本文采用卡尔曼滤波的方法对原始数据集进行滤波降噪处理,输出高质量的数据集,为 PCA 建模提供基础。图 3 所示为 AHU 模型建立及故障诊断流程。

图3 模型建立及故障诊断流程图
PCA 模型建立可以分为以下3 个部分:
1)原始数据采集及滤波降噪,通过对收集到的数据矩阵X720x9进行滤波处理,将无效数据、极端高低频数据阈值控制,降低数据的噪声后,最大限度还原系统运行稳定性。
2)优化后的数据集一部分用来模型的训练,建立PCA 模型,求出主元数,并计算出平方预测误差的阈值δ2。
3)计算每个监测数据的Q统计量和T2统计量,利用平方预测误差的阈值δ2来确定系统的故障率,若平方预测误差>δ2,则系统出现故障,并求出故障检测率,反之则没有出现故障。
2.2 滤波前后数据分析
由于变风量空调系统具有高度的非线性的特点,而AHU 中能够描述系统运行的变量有很多,因此建立精确的解析模型很困难。PCA 模型不需要准确的内在关联式,完全基于数据集来确定问题,直接用数据的变化发现和解决问题。
PCA 模型一般需要训练集和测试集,通过历史数据集的训练来确定模型,测试集一般是在线监测的数据导入模型进行验证,来确定故障是否发生。为了方便验证,前504 个样本作为训练集,后 216 个样本为测试集。实验故障数据的获取需要大量的金钱成本,这里人为在第118 个样本后加入故障,以测试模型检测故障率。模型训练具体过程如下:
1)将原始数据进行无量纲化处理,使每个变量被赋予相等的权重。经处理后,原始数据矩阵X的均值为0,方差为1。
2)求解特征值和特征向量,并求出以特征值所对应的特征向量矩阵P。
3)根据累计贡献率 0.85 的原则,确定主元数k。主元数的个数直接影响到PCA 故障检测的能力,假设主元数选取过小,主元模型会丢失大量信息,而主元数选取过大,测量数据中的故障和噪声信息过多地保留在主元模型内,减弱了故障检测的能力。
4)计算投影矩阵C。
5)根据0.90 的置信区间求出了平方预测误差阈值δ2。
表1 为滤波PCA 模型下的特征值,贡献率及累计贡献率。

表1 滤波PAC 下的特征值,贡献率及累计贡献率
从表 1 中可以看出 9 个变量的贡献率依次减小,滤波 PCA 模型在主元数为 6 的时候贡献率仅为4.8%,累计贡献率89.6%,根据累计贡献率85%的的原则,主元数k=5。选择主元分析的个数为5 个既减少了主元数量又保留了系统的主要信息。因此这里系统故障检测采用滤波的PCA 模型。
3 系统故障检测
3.1 模型验证
为了验证模型的正确性,采用正常运行数据的70%作为模型训练集,后 30%作为测试集,测试结果如图4 所示。

图4 PCA 模型测试结果图
从后30%的测试集结果看,全部的 216 个数据都落在了T2 统计量和Q统计量阈值以下,验证了模型是可以正常运行并进行故障检测诊断的。
3.2 偏差故障5%检测
为检验 PCA 模型对空气处理机组故障的检测能力,在正常数据的基础上,人为引入不同部位、不同程度的故障,从测试集的第118 个数据起人为对送风温度、新风温度、冷冻水流量引入 5%的偏差故障,每个故障独立存在。
图5 送风温度传感器偏差故障中T2统计量虽然在 118 个样本有上升的趋势但是大部分都在阈值以下,不能作为故障检测依据,而Q统计量在 1~117 个样本都在阈值以下,从第 118 个样本起Q统计量骤然上升,且远远超过统计量阈值,检测率 100%,说明模型的故障检测可以以Q统计量作为依据。图6 新风温度传感器偏差故障中T2统计量在1~117 个样本全部低于阈值,在 118~216 个样本均超过阈值,而Q统计量在1~117 个样本也都全部低于阈值,从第 118 个样本后有95%的数据都超过了阈值。图 7 冷冻水流量传感器偏差故障中T2统计量趋势与图 5 基本相同,而Q统计量从第118 个样本后有90%的数据都超过阈值。

图5 送风温度传感器故障
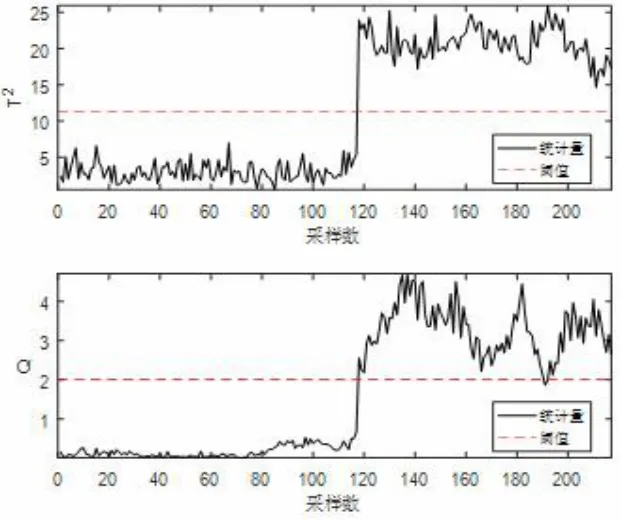
图6 新风温度传感器故障
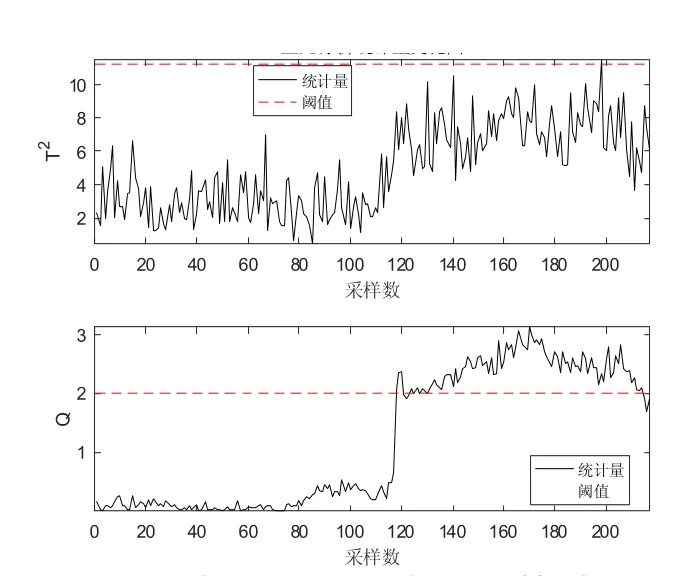
图7 冷冻水流量传感器故障
通过表 2 分析?,T2统计量在送风温度传感器故障和冷冻水流量传感器故障中均不能正确检测,而Q统计量在三种故障中的检测率均大于 90%,故使用Q统计量的PCA 模型可以用于空气处理机组故障的检测。

表2 统计量检测率
4 系统故障诊断
故障被检测出来后只能确定系统发生了故障并不能找出故障的来源,因此下一步要进行故障诊断。神经网络是受到生物神经网络启发的数学模型,它模仿人类神经元系统,以获得学习能力。网络从历史数据中学习,根据学习规则确定神经元之间的连接权值,使经过训练的网络能够产生正确的输出。BP 神经网络是最常用的神经网络之一,网络的第一层是一组包含来自所有输入变量的信息的输入层,第二层是包含一定数量神经元的隐藏层。每个神经元都有一个和算子和一个激活函数,执行非线性变换。
首先确定网络的输入输出层,输入层为表 3 故障模式中的数据,输出层为表 3 目标向量的数据,不同的故障模式对应不同的目标输出。本文将 720 组系统正常运行的数据划分成3 种故障数据,每种数据都要归一化处理,并对故障数据模式进行 1~3 编号,利用构建好的BP 网络进行训练。而后将待诊断的360 个数据归一化预处理后带入模型进行诊断,图9 所示为故障诊断结果图。从图中可以看出第二类故障(新风温度传感器故障)和第三类故障(冷冻水流量传感器故障)诊断率为 100%,第一类故障(送风温度传感器故障)诊断率达到了 92%。送风温度相比较于新风温度和回风温度它的要求精度更高,因此故障诊断率没有达到 100%,但是三种故障的检测率都超过了 90%,故BP 神经网络算法可以有效地对 AHU 系统进行故障诊断。

表3 不同故障模式输入输出

图9 故障类型诊断
5 结论
本文以某工厂变风量空调系统的 AHU 空气处理机组为研究对象,利用系统正常运行大数据建立模型,利用模型对故障来源进行诊断,主要得出了以下几个结论:
1)通过系统运行正常数据的前70%进行 PCA 建模,后 30%数据验证模型正确性,结果表明模型是可以正常运行并进行故障检测的。
2)T2统计量在送风温度传感器故障和冷冻水流量传感器故障中均不能正确检测,而Q统计量在三种故障中的检测率均大于90%,故使用Q统计量的PCA模型可以更好的用于空气处理机组故障的检测。
3)使用 BP 神经网络算法对系统故障进行诊断,新风温度传感器故障和冷冻水流量传感器故障诊断率均达到了 100%,新风温度传感器由于精度较高检测率为92%,说明算法对数量级较大的故障类型有更好的诊断率。

