色散补偿光纤中振幅对双孤子相互作用及传输的影响

靳海芹，陶军晖，李 杰，杨顺风，郝胜男，张 科，龚小宇

(湖北第二师范学院 物理与机电工程学院 ,武汉 430205)

孤子，又称孤立波，是一种在传播过程中形状、幅度和速度都维持不变的脉冲状行波,是一种特殊形式的超短脉冲，利用光孤子特性可以实现超长距离、超大容量的光通信，光孤子在全光控制、全光网络及量子测量方面也有广泛的应用前景。光孤子进行非简谐运动，极化形成电偶极子，其极化强度对光场强度存在一定的非线性依赖关系。激光器输出功率较低时，极化强度较弱，非线性效应的影响较小，而随着激光器的输出功率不断加大，光脉冲不断变窄，电偶极子的极化强度就不断加大，非线性效应的作用就变得明显起来。而色散补偿光纤的出现不仅克服了非线性效应，还克服了光纤中的色散。 色散补偿光纤[1]是一种具有较大负色散系数和负色散斜率的特殊光纤，色散补偿技术[2][3]的概念可用薛定谔方程中的脉冲传输方程来理解。关于脉冲传输方程的求解问题，大体上可分为解析解法和数值解法两类，本文主要运用对称分布傅里叶方法[4]，从数值模拟的角度来初步探讨在色散补充光纤中孤子对在不同振幅调制下的相互作用及传输特性。这将为后续进一步研究各调制参数对双孤子相互作用及多孤子相互作用[5][6]及传输特性的影响提供一定的理论及数值参考。

1 理论模型

光孤子的形成缘于自相位调制和群速度色散的相互作用，其行为可以用非线性薛定谔方程[7][8]进行描述，当考虑三阶色散效应和损耗时，孤子脉冲的描述可以用下式来进行：

(1)

其中，u(ξ，τ)是光脉冲包络函数，α代表光纤损耗系数，β2为群速度色散参量，β3为三阶色散参量。

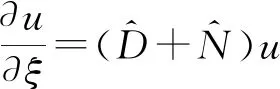
其中：分别是代表线性介质的色散和损耗的线性算子以及代表非线性效应的非线性算子。

色散补偿光纤中，三阶色散效应的影响很小，可以忽略不计，此时可令β3=0；如果不考虑光纤损耗则可令α=0。此时(1)式可以化简为：

(2)

2 研究方法

目前对光孤子传输的研究手段多种多样，数值模拟是其中的重要组成部分。由于非线性薛定谔方程是个非线性偏微分方程，一般情况下很难求出解析解，而它的数值解相对容易得到。常用的数值分析方法包括分步傅里叶法、差分法、微扰法、逆散射法、迭代算法等。其中，对称分步傅里叶法，由于其简便、易于运算和编程而被广泛使用。

对称分步傅里叶法的主要思想是：将光纤分为许多小段进行研究，在每一小段依次考虑线性效应和非线性效应，并依次类推下去，最后计算出结果。

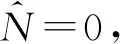
则其数学表示为：

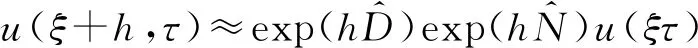
(3)

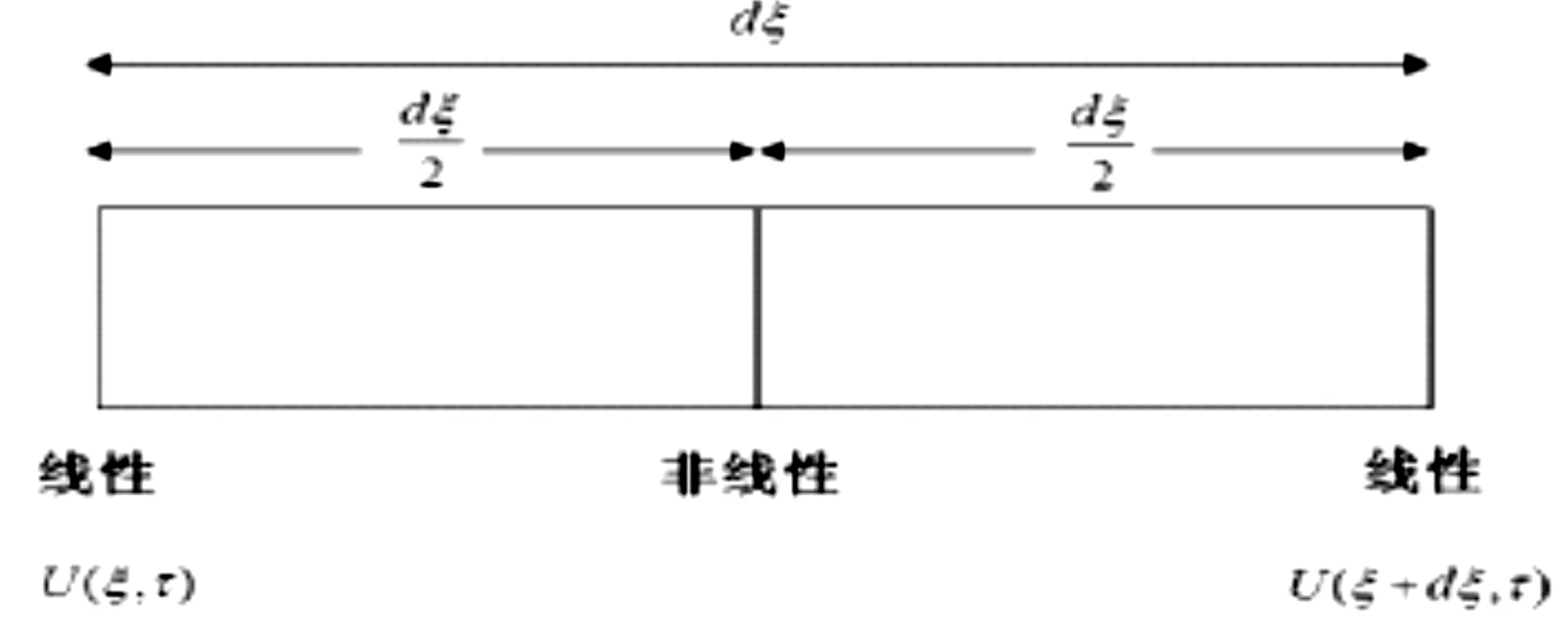
图1 分步傅里叶方法示例

(4)

(Ⅰ)非线性步：u1=exp(hi|u|2)u(ξ，τ)

(5)

(Ⅱ)对u1求傅里叶变换：u2=Fu1

(6)

(7)

(Ⅳ)对u3求傅里叶逆变换：u(ξ+h，τ)=F-1u3

(8)

按照步骤(5)-(8)式对(2)式中的孤子脉冲进行振幅参数调制及数值分析。

3 数值分析

3.1 基态孤子传输情况

首先，我们先来看只有单一的输入信号时基态光孤子的传输情形。

设定输入信号波形为：u(0，τ)=sech(τ)

(9)

输入输出结果如图2。

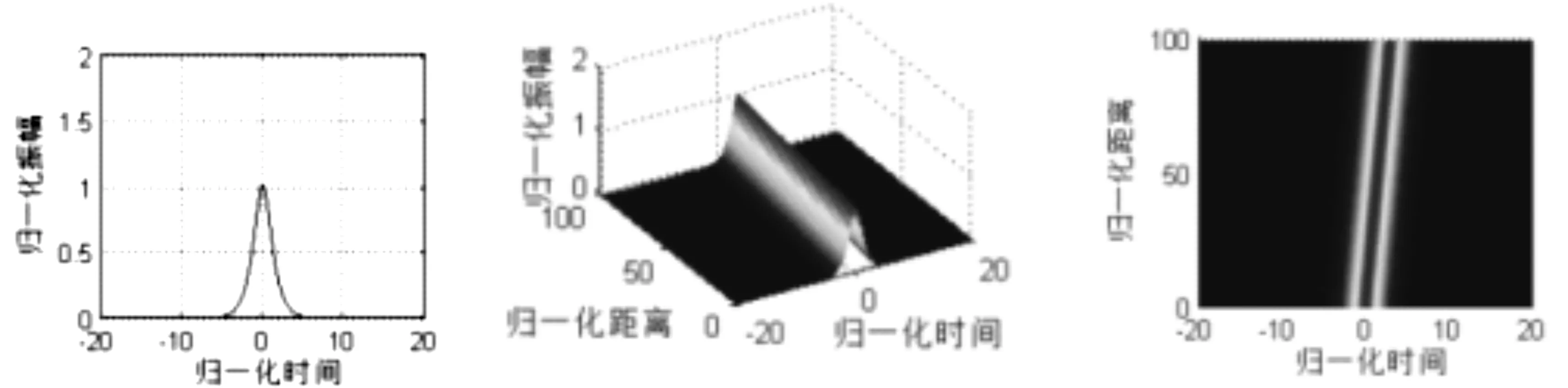
图2 色散补偿光纤中基态孤子传输

图2 为基态孤子在色散补偿光纤中的传输情况，图中自左至右分别表示输入波形的二维平面图、输出波的三维立体图以及输出波形的二维俯视图。由图2我们可以看出，对于基态孤子，其强度和波形在传输过程中将一直是基本保持不变进行传输的，非线性效应和色散效应一直是平衡的，这正是光孤子适合用作信息传输载体的原因之一。

在色散补偿光纤中，信息传播时不可能是以单个孤子载体的形式传播的，而必须是以孤子串进行传播。在这种情况下，孤子与孤子之间也会发生作用，从而可能影响传输带宽。因而研究传输过程中多孤子的相互作用情形很有必要。

4.2 色散补偿光纤中振幅对双孤子相互作用的影响

4.2.1 同幅同相的双孤子间的相互作用

为了了解验证双孤子(或孤子对)间的相互作用，首先对两个同幅同相的孤子间的相互作用进行模拟。

输入波形为

u(0，τ)=sech(τ-q0)+r1sech(r1(τ+q0))exp(iθ)

(10)

其中：q0表示两个孤子的半间距，r1表示相对振幅，θ表示相对相位。

按如下方式设置参数：q0=3，θ=0，r1=2.

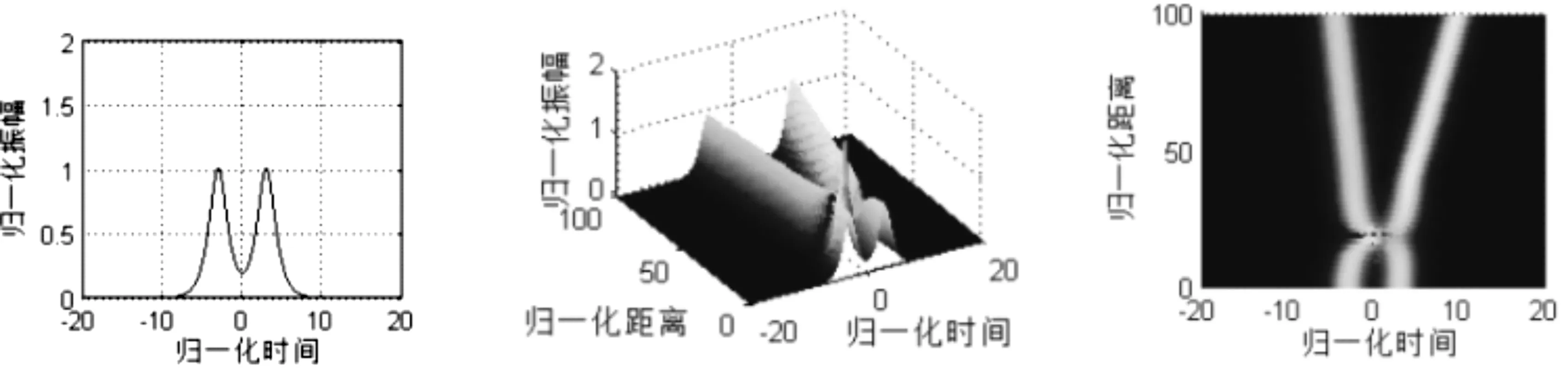
图3 色散补偿光纤中同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1)

图3是色散补偿光纤中同幅同相孤子对传输情况，其中，图中自左至右分别表示输入波形的二维平面图、输出波的三维立体图以及输出波形的二维俯视图。由图3可以看出，孤子与孤子间的距离发生了变化，孤子对之间的相互作用表现为吸引—碰撞—排斥。

4.2.2 不同幅同相的孤子对间的相互作用

由于同幅度同相的孤子对波形发生变化影响到相邻的脉冲波形，所以要想将光孤子作为信息载体投入实用就必须设法减小这种相互作用。如果能通过控制输入信号来达到减小孤子间的相互作用的目的那无疑之最直接、最简单的方式。

对式(10)进行观察，影响相邻两个孤子的参数主要有3个：相对振幅r1，相θ，对相位间距q0。不妨从这三个方面进行考虑。

首先观察相邻两个孤子的不同幅度对其相互作用的影响。

将输入式(10)中的参数设置如下：q0=3，θ=0，r1分别取1.1，1.2，1.3，1.5，1.7.

(a)q0=3，θ=0，r1=1.1时

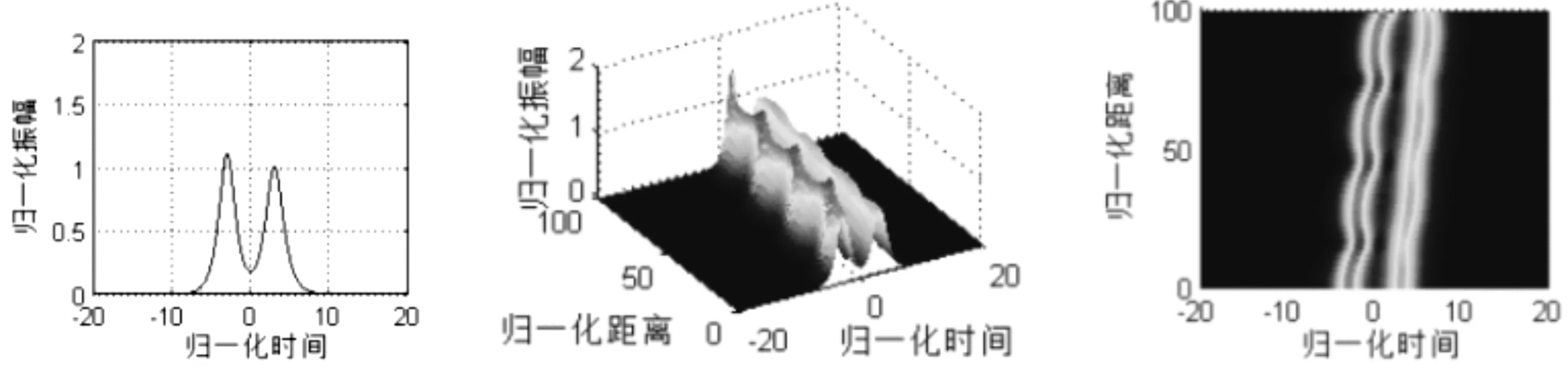
图4 色散补偿光纤中不同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1.1)

(b)q0=3，θ=0，r1=1.2时

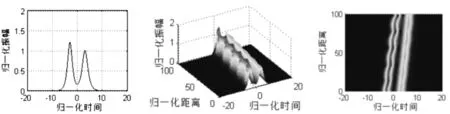
图5 色散补偿光纤中不同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1.2)

(c)q0=3，θ=0，r1=1.3时

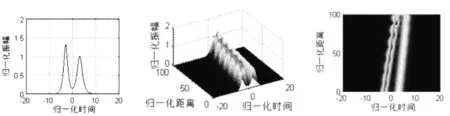
图6 色散补偿光纤中不同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1.3)

(d)q0=3，θ=0，r1=1.5时

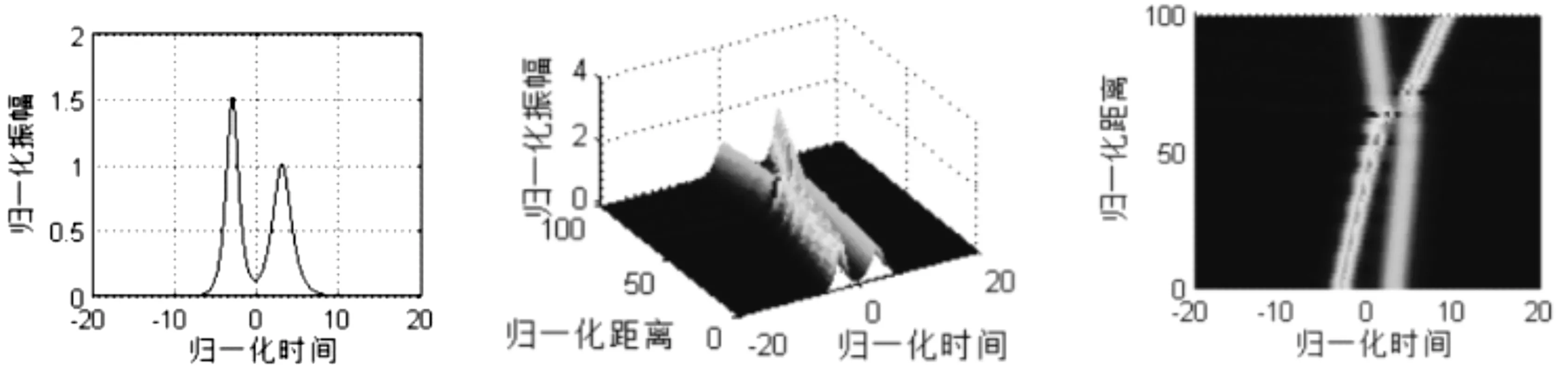
图7 色散补偿光纤中不同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1.5)

(e)q0=3，θ=0，r1=1.7时

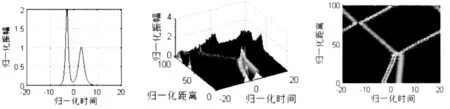
图8 色散补偿光纤中不同幅同相孤子对相互作用情况(q0=3，θ=0，r1=1.7)

图4-图8分别为相对振幅取1.1、1.2、1.3、1.5、1.7时的情况，自左至右分别为输入波形的二维平面图、输出波的三维立体图以及输出波形的二维俯视图，将图4-图8中相应的图进行对比，可以看出，随着相邻孤子对之间相对幅度的增大，孤子与孤子表现出吸引—碰撞—排斥的模式更强，其中相对幅度较大的孤子的波形变化较大，且在孤子间振幅差相对较大的情况下，孤子波形运动轨迹发生了交叉现象，如图7，甚至孤子间碰撞后发生毁灭的现象，如图8。所以孤子间的相对幅度越大，它们的波形受到相互作用越强，特别是归一化振幅较大的孤子，其波形的波动与归一化振幅较小的孤子相比显得更加明显。但是，随着幅度差异减小，相邻孤子间的相互影响也逐渐减小。

5 结论

本节主要讨论色散补偿光纤中两个孤子间的相互作用，分析了输入信号相对振幅的变化对孤波的相互作用及传输的影响。发现减小孤子对之间的相对振幅(但不是等幅，因为孤子等幅时，孤子间相互影响比较大，如图3)时，孤子间的相互作用明显减弱，而其中振幅较小的孤子较振幅较大的孤子而言，波形更稳定。由此可见，减小孤子间的相对幅度是抑制孤子间相互作用非常有效的手段。这些均将为进一步研究双孤子在其他调制参数下的相互作用及传输、多孤子的相互作用及传输提供一定的理论参考。