小行星(469219) Kamo`oalewa轨道的确定与误差分析
田伟
(上海历元信息科技有限公司上海200241)
1 引言
太阳系内的小天体, 包括小行星、彗星等是未来深空探测的重要目标. 通过开展小行星探测任务有助于研究小天体的物质组成和运动规律、寻找太阳系起源和演化等基本天文学问题的答案, 同时也有助于实现小天体资源的利用和开发. 2019年4月19日中国国家航天局正式公布了中国小行星探测计划(见国家航天局“小行星探测任务有效载荷和搭载项目机遇公告”). 该计划将近地小行星(469219)Kamo`oalewa和主带彗星133P/Elst-Pizarro列为探测目标. 其中, 小行星(469219)Kamo`oalewa是2016年4月27日由夏威夷Haleakala天文台所发现. 长时间尺度的轨道动力学研究显示它是一颗绕日公转周期与地球相同、且在太阳-地球会合坐标系下围绕地球运动的近地小行星[1].
小行星(469219) Kamo`oalewa距离地球较近, 受地球和月球的摄动力显著, 且自身重力场微弱, 因此探测任务需要考虑的影响和约束不同于大行星[2–4]. 小行星历表是小行星探测任务规划和轨道设计的重要依据. 高精度的小行星历表可以确保探测器精确进入目标天体的引力影响区, 实施对目标小行星伴飞、绕飞和软着陆等高难度操作. 在应用历表约束时, 高精度的目标小行星历表也将有助于减少任务实施阶段探测器机动的次数和能量消耗.
小行星历表的精度一方面取决于观测数据类型、时间跨度和观测精度, 另一方面取决于动力学模型的准确性. 本文将首先根据小行星(469219) Kamo`oalewa的轨道特性,详细给出该小行星的轨道动力学模型, 并通过一个轨道积分实例对本文采用的动力学模型与美国喷气推进实验室(Jet Propulsion Laboratory, JPL)的Horizons在线历表系统采用的动力学模型进行比较(见第2部分). 然后介绍现有的光学观测数据. 再次, 给出数据处理方法和定轨结果. 最后, 结合我国小行星探测计划拟采用的时间窗口, 给出该小行星在[2020-01-01—2025-01-01]期间的轨道误差, 并探讨进一步改进该小行星历表精度的潜在途径.
2 动力学模型
小行星(469219) Kamo`oalewa是一颗近地小行星, 并且在未来几个世纪内将在太阳-地球会合坐标系下围绕地球运动[1], 因此在建立轨道动力学模型时, 需要充分考虑其轨道特性, 尤其是地月系统对其轨道的影响. 由于该小行星的几个主要物理参数(例如,反照率和密度等)测定精度低或尚未确定1https://ssd.jpl.nasa.gov/sbdb.cgi?sstr=469219, 本文暂时没有考虑太阳光压等非保守力对其轨道的影响.
本文采用了太阳系质心力学时(Barycentric Dynamic Time, TDB)作为积分系统的时间尺度. 空间坐标系为太阳系质心广域参考系, 其尺度和指向分别与TDB和国际天球参考架(International Celestial Reference Frame, ICRF)一致. 天文单位(au)取值为国际天文联合会(IAU)决议值149597870.7 km (IAU2012 resolution B2). 太阳、八大行星、月球和冥王星等主要天体的质量和状态向量与JPL行星/月球历表DE430所采用的数值保持一致. 在忽略非球形引力场的前提下, 太阳、月球、八大行星、冥王星对小行星(469219) Kamo`oalewa的引力作用(考虑一阶后牛顿近似下的相对论效应)由Einstein-Infeld-Hoffmann (EIH)方程给出[5]. 由此产生的加速度项可表述为:

其中, 下标A表示小行星(469219) Kamo`oalewa,µB和µC分别是天体B和C的质量与引力常数G的乘积,rAB=xB −xA和rAB=|rAB|分别是天体A和B之间的相对位置矢量和相对距离,xA(或xB)和˙xA(或˙xB)分别为对应天体A(或B)的位置和速度矢量. 相对位置矢量rAC和rBC的定义类似于rAB, 而相对距离rAC和rBC的定义类似于rAB, 以上各量均在太阳系质心广域参考系中给出.c=299792458 m·s−1为光子在真空中的传播速度.
考虑到该小行星在较长时间内绕地球运动(距离最近时仅为0.03332 au), 因此研究其轨道动力学演化时, 除了考虑主要天体(作为点质量)的引力作用外, 仍需要考虑地球和月球等天体的非球形引力场对其轨道的影响. 以地球为例, 其非球形引力场W(r,θ,λ)在地心地固参考系下可由一组Stokes系数(Clm,Slm)来表示[6]:
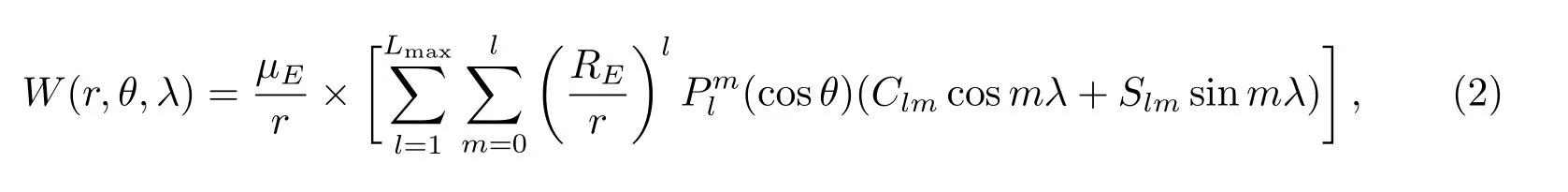
其中µE和RE分别是地球质量与引力常数的乘积和平均地球半径.Lmax为该天体非球形引力场的截断阶数. (r,θ,λ)是某场点P在地心地固参考系下的球坐标.是l阶m次的Legendre函数. 点质量天体B在场点P处受到的非球形引力场的引力作用产生的加速度为(在笛卡尔直角坐标系下):

其中上式右边第2个偏导数矩阵可通过球坐标(r,θ,λ)和笛卡尔直角坐标(X,Y,Z)之间的转换关系直接计算. 与相对应, 非球形天体因受到点质量天体B的反作用力而产生的反向加速度可表示为:

除地球的非球形引力场的影响外, 本文还考虑了月球和太阳的非球形引力场的影响(计算公式与(2)–(4)式类似). 其中地球和月球的低阶引力场分别取至5阶和3阶, 而太阳的非球形项仅考虑其J2,S(=−C20,S)项(见表1). 表1中地球和月球引力场参数主要通过卫星激光测距(Satellite Laser Ranging, SLR), 月球激光测距(Lunar Laser Ranging, LLR), 重力场测量计划Gravity Recovery and Climate Experiment(GRACE)和Gravity Recovery and Interior Laboratory (GRAIL)获得. 太阳、地球和月球的指向模型与JPL行星/月球历表DE430采用的模型保持一致[10].
关于太阳系内主要小行星引起的摄动效应, 本文考虑了5颗大质量小行星(Ceres、Pallas、Vesta、Iris和Bamberga)的影响. 其中主带小行星中质量最大的小行星Ceres、Pallas和Vesta的影响最为显著. 而小行星Iris和Bamberga对行星历表的影响仅次于Ceres、Pallas和Vesta[11]. 为了保证本文的小行星摄动模型与大行星历表中的小行星摄动模型具有较好的一致性, 文中的小行星摄动模型也考虑了小行星Iris和Bamberga的影响.
在动力学系统中, 这5颗小行星的轨道与目标小行星的轨道一同积分得到. 小行星参考时刻T0(简化儒略日57831.0,2017-03-19)的初始状态参数来自于JPL/Horizons在线历表系统. 数值积分系统同时积分计算了目标小行星的状态向量转移矩阵. 为了检验本文采用的动力学模型, 我们利用数值积分方法计算了[2000-01-01—2030-01-01]期间小行星(469219) Kamo`oalewa的轨道, 并与JPL/Horizons在线历表系统提供的轨道进行比对. 图1给出了本文的积分轨道与JPL轨道的差别(3个坐标分量上均小于1 km).考虑到地球与该小行星之间的平均距离约为2.5×107km, 1 km轨道差异约等价于测角差异0.008′′. 因此, 在后期处理地面光学测量(其拟合后观测残差的均方根误差约为0.2′′)时, 我们认为, 针对该小行星, 本文的动力学模型与JPL/Horizons在线历表系统的动力学模型无显著差异.

表1 地球、月球和太阳的非球形引力场参数和取值Table 1 Parameters of non-spherical gravitational field for the Earth, Moon and Sun,and their values
3 观测数据
本文采用的光学观测数据来自于国际小行星中心(Minor Planet Center, MPC)官方网站2https://www.minorplanetcenter.net. 这些光学数据由编号为F51、568、T12等望远镜观测得到. 由于观测数据稀少(尤其是该小行星尚未确定之前), 本文没有对观测数据进行剔除, 而是假设每次观测为等精度观测, 且互不相关. 尽管采用的数据从2004到2018年覆盖了多个轨道周期, 但由于观测量稀少且集中于某几个观测窗口, 目前JPL/Horizons在线历表系统基于MPC提供的光学观测数据给出的小行星(469219) Kamo`oalewa的轨道精度约为数十公里(在某些时段可达到上百公里)3https://ssd.jpl.nasa.gov/horizons.cgi.

图1 本文轨道积分结果与JPL/Horizons在线历表系统生成的小行星(469219) Kamo`oalewa历表之间的差异,(x,y,z)和(vx,vy,vz)分别是该小行星在太阳系质心参考系下的位置和速度. 起始积分时刻T0为简化儒略日57831.0(2017-03-19).Fig.1 The difference between ephemeris of the asteroid (469219) Kamo`oalewa provided by JPL/Horizons system and that integrated from the dynamical model in this work, (x,y,z) and(vx,vy,vz) are position and velocity of the asteroid in the global reference system centred at solar system barycentre. The integration starts at the moment T0: Modified julian day 57831.0 (2017-03-19).
4 数据分析与定轨结果
光学资料的数据分析采用了经典最小二乘原理下的批处理方法[12–13]. 在建立观测方程时采用了太阳系质心参考系, 即利用太阳系质心参考系下地球和目标小行星的坐标计算观测量的拟合前残差O–C(观测量的测量值减去理论计算值), 和计算观测量相对于目标天体的(在T时刻)状态向量和其他敏感参数的偏导数, 并建立观测方程. 本文的被估计参数仅包括了该小行星在参考时刻T0处的状态参数(位置和速度).
由于MPC光学观测数据并没有给出每个观测数据相应的观测精度, 本文基于每个光学观测量为等精度且互不相关的假设, 权矩阵选取为单位矩阵. 最后, 我们利用最小二乘原理解算出法方程. 由于观测方程的建立和状态转移矩阵的计算过程中均采用了线性化近似, 在利用最小二乘原理确定初始轨道参数时需要进行迭代运算. 表2给出了目标小行星在参考时刻T0的状态参数(迭代次数为3). 图2给出了光学观测在赤经和赤纬方向上的拟合后观测残差分布. 在赤经和赤纬方向上拟合后观测残差的均方根误差分别为0.22′′和0.13′′. 图中“JPL/Horizons”代表基于JPL/Horizons在线历表系统提供的小行星历表计算的残差. 如图可见, 本文的残差分析结果与JPL/Horizons相当,在处理2004年间的两个数据点时有所改进. 这可能是由在数据分析时对测量值的权重分配引起的. 本文假设2004年间的两个数据点的观测误差与其他年份相等, 即具有相同的权重. 如果对2004年间的数据进行降权处理, 相应数据点的偏差会增大. 目前尚未发现介绍JPL/Horizons解算该小行星轨道时观测量权重的分配机制的文献, 为了推测JPL/Horizons解算小行星轨道时的观测量权重的分配机制, 需要进一步比较和分析多颗小行星轨道的解算结果.

表2 T0时刻小行星(469219) Kamo`oalewa的初始位置、速度和两者的中误差(3σ)Table 2 Initial position and velocity of the asteroid (469219) Kamo`oalewa at T0 and their standard deviations (3σ)
在实际应用中, 我们可能对未来某特定时刻或时段该小天体的位置和精度更感兴趣. 本文利用(线性化)协方差转移映射法[14]将小天体状态向量的协方差矩阵从参考时刻传递到其他时刻, 比如小行星探测任务执行期间的某一时刻. 图3给出了2020年至2025年间该小行星的轨道误差(3σ).
需要说明的是, 本文给出的精度均为内符合精度. 由于动力学模型误差和观测量的随机模型误差(或观测量权重的不准确性)等的影响, 内符合精度仅能作为其真实精度的一个参考. 外推精度仍需要利用其他方法, 比如统计外推期间实测数据的残差分布等,做进一步评估.
5 总结与展望
本文以小行星(469219) Kamo`oalewa为例, 考虑其轨道特性, 建立了一套精度与JPL/Horizons在线历表系统(小行星历表部分)相当的小行星轨道动力学模型. 在现有光学观测数据的基础上, 对该小行星的轨道参数进行估计, 并给出了该小行星在外推区间内[2020-01-01—2025-01-01]的轨道误差.
进一步提高该小行星的轨道精度有赖于更多的光学观测和其他类型的观测资料,比如无线电雷达测距等. 针对小行星(4179) Toutatis, 国内外学者在利用光学和雷达数据确定其轨道时发现, 对具有较短观测历史的小行星, 即使少量的雷达测距/测速数据也可以显著改善其轨道精度[15–16]. 因此可以预期, 雷达测量的引入将会对目标小行星(469219) Kamo`oalewa的轨道改进起到重要作用. 我们在分析被估计参数的协方差矩阵时, 发现状态参数之间具有强相关性(见表3). 初步分析表明, 这种强相关性主要由两方面因素引起, 一方面是光学观测数据稀疏和观测时段覆盖不均匀, 另一方面是由于缺少互补的观测数据(比如, 测距/测速数据等). 具体原因有待进一步研究.
本文仅研究了小行星(469219) Kamo`oalewa在短时间尺度下的动力学演化. 工作的局限体现在建立动力学模型时忽略了太阳光压、Yarkovsky效应以及银河系潮汐作用等对小行星轨道具有长期影响的因素[17], 同时也反映在轨道误差分析时, 采用了仅适用于短时间尺度的(线性化)轨道误差传递映射.

表3 T0时刻小行星(469219) Kamo`oalewa的状态向量之间的互相关系数Table 3 Correlation coefficients between initial state parameters of the asteroid(469219) Kamo`oalewa at T0
长时间尺度下小行星(469219) Kamo`oalewa的动力学演化是一个非常重要的研究方向. 我国小行星探测任务的开展将提供近距离观测该小行星的机会. 这不但有助于我们研究其动力学机制、内部结构和物理特性等, 而且通过精确测定其物理参数, 也将有助于研究长时间尺度下近地小行星的动力学性质(比如, 小行星的长期演化和起源问题).
本文生成的小行星(469219) Kamo`oalewa历表数据可通过邮箱联系作者获取.
致谢感谢国际小行星中心提供的在线数据下载服务和JPL/Horizons系统提供的在线历表服务. 感谢暨南大学彭青玉教授的讨论和建议. 感谢审稿人提出的宝贵意见.

