基于PPA-POT的RCCD变形监测控制值拟定方法

赵二峰 李波 朱延涛

摘 要：在碾压混凝土坝（RCCD）长期服役过程中，变形是能够直观反映大坝工作性态的主要性能参数之一。为了有效监控大坝运行状态，有必要对坝体变形拟定监测控制值。为突破传统单一测点指标拟定的局限性，针对碾压混凝土坝变形空间结构关联分布特性，构建了多测点融合的坝体变形场模型，利用投影寻踪方法（PPA）确定各测点权重，在此基础上，利用POT模型进行监测控制值的拟定。工程应用结果表明了本文方法的可行性与适用性。

关键词：碾压混凝土坝;变形场;监测控制值;投影寻踪方法;POT模型

Abstract：In the long service of Roller Compacted Concrete Dam （RCCD）， deformation is one of the main performance parameters which can directly reflect the working behavior of the dam. In order to effectively monitor the safety of dam operation， it is necessary to determine the monitoring control values for deformation. In order to overcome the limitations which the traditional dam deformation monitoring control values only consider the single point. This paper constructed a deformation field model of RCC dam with multi-measurement point fusion and used Projection Pursuit Analysis （PPA） to determine the weight of each measurement point according to the spatial structure correlation distribution characteristics of RCC dam deformation. On this basis， the POT model was proposed to determine the monitoring control values. The results of engineering application show the feasibility and applicability of the method in this paper.

Key words： roller compacted concrete dam; deformation field; monitoring control value; projection pursuit analysis; POT model

碾压混凝土坝（RCCD）筑坝技术特殊[1]，大坝变形作为能直观反映其运行性态的监测量，是监测和判断大坝运行性态的主要手段之一[2-3]。大坝变形表现为动态非线性[4]，深入挖掘大坝变形的演变规律具有重要意义[5]。变形指标是表征大坝工作状态是否正常和评价大坝安全与否的关键指标，可以通过监测效应量控制值来评估大坝的安全性。常用的估计监测效应量控制值的方法有数理统计法和结构分析法[6]，针对长期监测资料序列，通常采用数理统计法拟定大坝变形监测效应量控制值。顾冲时等[7]提出了龙羊峡混凝土坝三级监控指标拟定的原理和方法;丛培江等[8]建立了基于最大熵原理的大坝安全监控指标拟定模型;雷鹏等[9]通过构建空间变形熵，利用投影寻踪法（PPA）确定权重，采用传统数理统计法和结构分析法计算了混凝土坝整体变形熵预警指标。苏怀智等[10-11]研究表明，POT模型更加关注序列的超阈值分布情况，充分考虑所有较大测值出现的可能，计算得到的预警指标能客观反映工程实际。

大坝往往布置多个测点进行监测，但常规的大坝监测控制值多是依据单测点拟定的，忽略了测点间的空间关联性。充分考虑多个测点监测信息时间和空间分布的关联特性，综合反映大坝变形的整体性，可以更加有效反映大坝的整体工作性态。因此，构建碾压混凝土坝正倒垂线测点平面变形场，采用投影寻踪法将变形场数据投影到低维空间，并运用POT模型理论，根据Hill图和平均超额函数法综合确定阈值，可用于拟定坝体变形场的安全监测控制值。

1 碾压混凝土坝变形场模型构建及权重确定

1.1 碾压混凝土坝变形场模型

碾压混凝土坝坝体不同部位布置有大量监测仪器，共同监测大坝工作性态。实际上，各个测点的变形并不是独立的，而是在外荷载作用产生的结构效应上相互关联的，即存在空间结构上的关联性。因此，需要综合考虑不同空间监测效应量之间的關联性，从数据中挖掘出大坝变形的空间特征及发展规律。以往较少考虑单测点与其他测点的相对空间位置，随着空间计量学的发展，数据的表征方法已经从一维（时间或横截面）扩展到了高维（空间面板数据，横截面、时间和空间数据相结合），为碾压混凝土坝变形场的构建提供了数学基础。

针对碾压混凝土坝布置的正倒垂线测点特性，在外荷载作用下产生的位移矢量场δ可分解为水平顺河向位移δu、水平横河向位移δv，即：

大坝同一时刻所有测点的监测值可以总体上反映结构系统的空间变形性态。对于碾压混凝土重力坝典型坝段或拱坝整体变形的垂线测点而言，比如对某一条垂线上所有测点的顺河向或横河向变形进行连续监测，进而可以得到n个不同高程在T个不同时刻的顺河向或横河向变形值δ，即

1.2 测点权重的确定

投影寻踪法可将高维的监测数据投影到低维空间，低维数据是研究和分析原高维数据得出的，能反映原高维数据特性的投影向量。所有位移测点的样本可以表示为{δij|i=1，2，…，n;j=1，2，…，T}，δij为第i个高程测点的第j个测值。对δij按越大越优的指标进行归一化处理得到δij：

基于实数编码的加速遗传算法（RAGA）[12]优化求解目标函数，具体步骤：①归一化处理，并把变量随机分成a组，本文取13组;②计算每组目标函数值h（l），并按从小到大的顺序排序;③计算目标函数值h（l）的适应度;④按比例进行选择操作，产生子代群体;⑤对种群进行杂交操作，产生第二代群体;⑥对种群进行变异操作，产生第三代群体;⑦进行迭代，对上述步骤得出的子代群体按适应度值排序，取前10～160的子代转步骤③进行下一次迭代演化;⑧将迭代第一次、第二次所得到的变量变化区间作为变量新的区间，转步聚①，反复运行上述步骤，直到满足结束条件，结束整个算法运行。

将求得的最佳投影方向记为l*，按照式（5）求得样本点的投影值，对投影值处理可得到各测点的权重值：

2 基于极值理论的坝体变形监测控制值拟定

变形监测数据一般具有较长的时间序列，极值理论中的POT模型关注序列的超阈值分布，考虑了可能出现的所有较大值，能够更好地体现不利工况下测值样本的分布特征。

2.1 POT模型

Pickands[13]在极值理论中引入了POT模型，该模型将超出给定阈值的观测值作为样本，利用广义Pareto分布研究样本中超阈值量的分布形式。考虑大坝不利工况，将极值理论应用于变形监测控制值拟定，POT模型对监测数据先选择合适的阈值，并应用广义Pareto分布对超过阈值的数据序列进行拟合。设有一组样本数据x1、x2、…、xn，其分布函数为F（x），取阈值为u，则超过u的超限值子序列个数为nu，那么超限值yi=xi-u的分布函数Fu（y）的表达式为

2.2 广义Pareto分布的参数估计

拟定大坝安全变形监测控制值，采用POT模型需先确定阈值u的大小，再研究超阈值样本分布。尺度参数与形状参数估计的方法主要有Hill图法、平均超额函数法等[14]。

（1）Hill图法。设x1、x2、…、xn是n个独立同分布的正的随机变量，其倒序统计量为xn，n≥xn-1，n≥xn-2，n≥…≥x1，n，Hk，n为样本序列的Hill估计：

（2）平均超额函数法。采用监测数据的平均超额函数图计算u。当形状参数ε<1时，广义Pareto分布的平均超额函数可以由线性函数e（m）表示：

3 工程实例

某水电站工程属Ⅰ等大（1）型工程，其主要挡水建筑物为碾压混凝土重力坝，测点布置见图1。坝顶高程为1 334 m，坝顶长为516 m，最大坝高为168 m，大壩共分为24个坝段，①～⑨和B17～B24分别为左岸和右岸挡水坝段、B11～B15为溢流坝段、⑩和B16为中孔坝段。选择中部B13坝段的正倒垂线PL1～PL4和IP5（测点高程分别为1 334、1 294、1 254、1 205、1 180 m），用于监测坝体变形情况。将正垂PL1～PL4和倒垂IP5测点2015年7月23日至2019年12月31日顺河向位移数据（共1 623个）作为数据样本，剔除粗差，各测点实测位移过程线见图2。

3.1 坝体变形场各测点权重确定

通过投影寻踪算法，将坝体变形场中的多维数据降维得出5个测点的投影权重wi，PL1～PL4和IP5测点的权重分别为0.293、0.260、0.150、0.149、0.148。根据PL1～PL4和IP5测点数据由式（3）得到坝体变形的综合位移，见图3，综合位移过程线集成了整条正倒垂线测点的监测数据，能体现整个坝段水平位移的变化机制和周期性变化规律。

3.2 变形监测控制值拟定

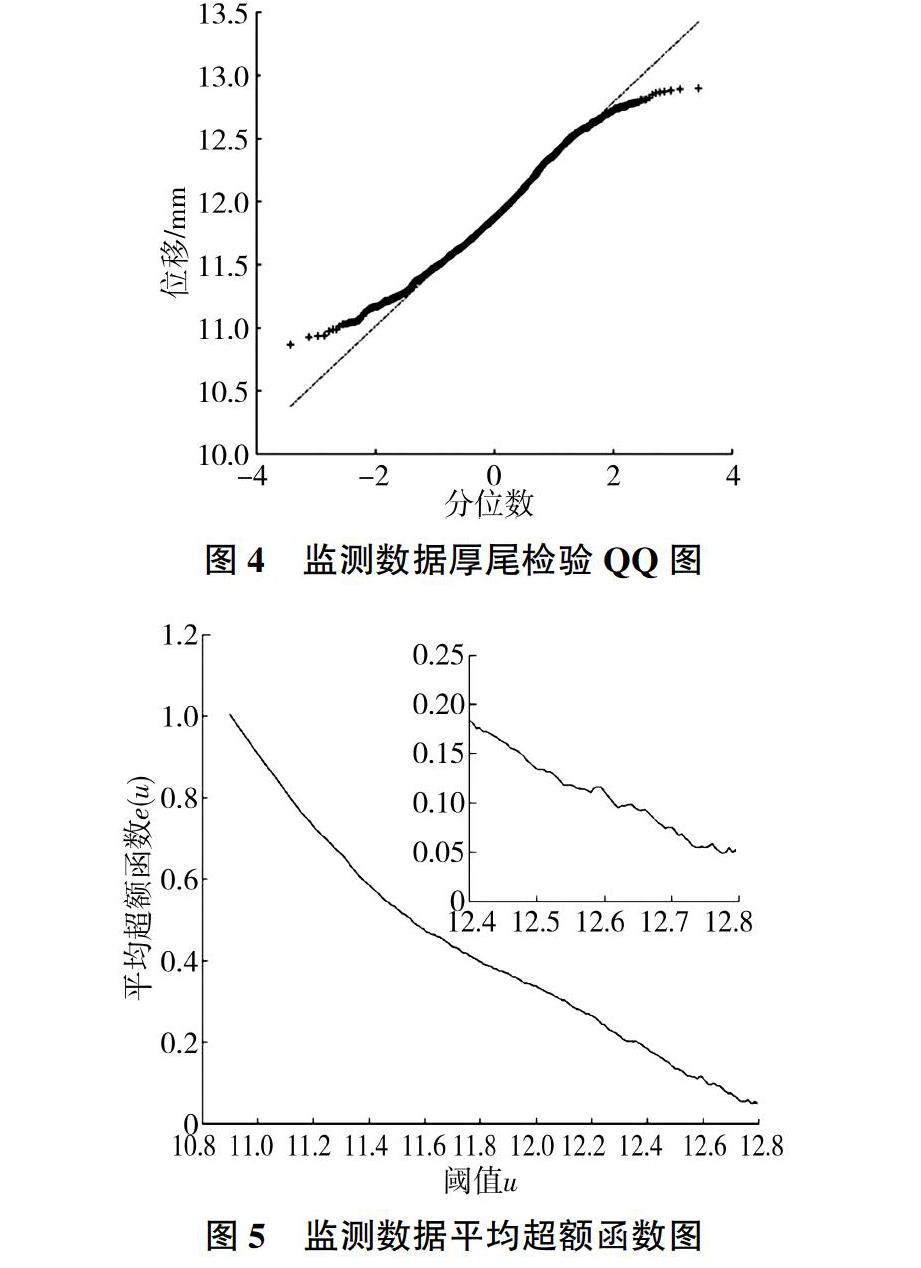
（1）POT模型计算结果。对上述综合位移序列进行分析，通过QQ图法[14]对样本数据进行厚尾检验，结果见图4。由图4可知位移序列中间部分近似直线，呈微凹型，下端向左翘起，上端向下弯曲，符合厚尾分布特征，满足极值POT模型成立的前提条件。利用平均超额函数法与Hill图法对阈值进行拟定，分别绘制平均超额函数图与Hill图（见图5、图6），据此2幅图确定阈值。根据图5可知，阈值u在整个变化过程中，超额函数变化趋于稳定，且u在12.59附近超额函数与阈值存在正相关关系，u>12.60时，图像总体呈下降趋势。由图6可知，超阈值个数nu取94时，Hill图趋于稳定。

POT模型计算参数见表1。大坝变形异常发生概率的确定具有一定经验性，其值可根据大坝重要性确定[6]，由于该工程为大（1）型工程，因此取大坝变形异常发生概率为1%，计算其变形监测控制值。通过式（17）推求出该碾压混凝土坝变形监测控制值δ⌒m=13.02 mm。

（2）典型监测效应量的小概率法。根据大坝的具体情况，选择不利于强度和稳定的荷载组合所对应的监测效应量，本文取2015—2019年的极大值，分别为12.39、12.69、12.89、12.90、12.51 mm。利用K-S法对综合位移极大值序列进行检验，满足正态分布，得出均值δ-=12.678 mm，标准差0.226 mm，大坝变形异常发生概率为1%的情况下，监测控制值δ⌒m′=13.20 mm。

（3）BMM分块模型。取每季监测值极大值组成的序列，每年按1—3月、4—6月、7—9月、10—12月划分为4季度，共18个数据，对序列拟合GEV分布[11]，计算GEV分布参数σ、ε、u分别为0.582、-0.308、12.283，从而可得该序列的总体分布函数，根据式（18）可得拟定的监测控制值为δ⌒m″=13.05 mm。

4 结 论

针对碾压混凝土坝变形的空间结构特性和发展规律，根据数据内在规律和特征提出了多测点融合的坝体变形场模型，并采用投影寻踪法确定了各测点权重，在此基础上，提出了利用极值理论中的POT模型进行碾压混凝土坝变形监测控制值拟定的方法。

通过所提出的变形场综合位移计算公式得到整个坝段的综合位移，可以有效反映坝体变形整体情况，相比单测点建模更为高效。工程实例表明，由于超阈值的样本序列包含了次较大值，超阈值序列的数据分布能很好反映大坝抵御已经历荷载作用的特性，基于超阈值样本拟定的监测控制值是适宜的。与传统方法相比，验证了本文方法的有效性，所得到的监测控制值更加偏于安全。

参考文献：

[1] 顾冲时，吴中如，吴相豪.碾压混凝土坝安全监控理论和方法[J].水利学报，2002，33（9）：112-116.

[2] 袁冬阳.基于多元时空信息挖掘的混凝土重力坝变形体征监控方法[D].南昌：南昌大学，2019：62-64.

[3] 汪亚超，方国宝，陈小虎，等.混凝土重力坝抗滑稳定实时分析方法[J].人民长江，2013，44（20）：37-41.

[4] 康传利，陈洋，张临炜，等.小波和混沌神经网络在大坝变形预测中的应用[J].人民黄河，2020，42（3）：101-104，116.

[5] 周兰庭，徐长华，袁志美，等.基于CEEMDAN-PSR-KELM的大坝变形预测[J].人民黄河，2019，41（6）：138-141，145.

[6] 顾冲时，赵二峰.大坝安全监控理论与方法[M].南京：河海大学出版社，2019：286-289.

[7] 顾冲时，吴中如，阳武.用结构分析法拟定混凝土坝变形三级监控指标[J].河海大学学报（自然科学版），2000，28（5）：7-10.

[8] 丛培江，顾冲时，谷艳昌.大坝安全监控指标拟定的最大熵法[J].武汉大学学报（信息科学版），2008，33（11）：1126-1129.

[9] 雷鹏，常晓林，肖峰，等.高混凝土坝空间变形预警指标研究[J].中国科学：技术科学，2011，41（7）：992-999.

[10] 苏怀智，王锋，刘红萍.基于POT模型建立大坝服役性态预警指标[J].水利学报，2012，43（8）：974-978，986.

[11] 聂兵兵，赵二峰，殷详详，等.基于极值理论的大坝变形监控指标拟定[J].水电能源科学，2015，33（12）：101-104.

[12] 金菊良，杨晓华，丁晶.基于实数编码的加速遗传算法[J].四川大学学报（工程科学版），2000，32（4）：20-24.

[13] PICKANDS J. Statistical Inference Using Extreme Order Statistics[J]. The Annals of Statistics， 1975（3）： 119-131.

[14] 劉莎莎.POT模型阈值的选取及应用[D].长春：吉林大学，2014：12-13.

【责任编辑 吕艳梅】