基于热力学的HTPB/AP复合底排药损伤本构模型及损伤差异分析

武智慧,牛公杰,钱建平,*,刘荣忠

1. 南京理工大学 机械工程学院,南京 210094 2. 中国工程物理研究院 总体工程研究所,绵阳 621999

HTPB/AP复合底排药(Composite Base Bleed Grain,CBBG)是一种颗粒填充高聚物,是底排增程技术的关键动力源。HTPB/AP CBBG主要成分为高氯酸铵(Ammonium Perchlorate,AP)和端羟基聚丁二烯(Hydroxyl-Terminated Polybutadien,HTPB),其余成分为固化剂、增塑剂等。发射工况下, HTPB/AP CBBG经历轴向高过载、膛压引起的压缩高过载和炮口处急速泄压引起的拉伸高过载等冲击载荷。这种恶劣的载荷工况将导致模量较低的HTPB/AP CBBG产生大变形,诱使初始损伤恶化,进而破坏药柱结构完整性,影响药柱燃烧规律,降低增程效率,削弱底排增程弹的战术性能。同时,战场环境温度变化引起的温度载荷(233～323 K[1])使得HTPB/AP CBBG的黏性特征凸显,其力学响应的差异性进一步扩大。明确HTPB/AP CBBG在不同应变率(特别是冲击载荷)及温度载荷下的力学性能,建立本构模型是进行HTPB/AP CBBG结构完整性分析的基础。HTPB/AP CBBG内部包含一个复杂的力学体系,颗粒与基体的界面粘接特性[2-3],颗粒、基体本身的力学性能[4],空穴[5]、颗粒破碎[6]等形式的损伤,黏性形变引起的升温软化[7-8]等因素均影响材料整体在外载下的宏观力学响应。可见,对HTPB/AP CBBG进行本构建模具有一定的挑战性。

近年来,学者们已逐渐深入开展针对HTPB/AP CBBG力学特性的研究工作。刘志林等[9]测试了室温下应变率为2 900～4 300 s-1时HTPB/AP CBBG压缩力学性能,对其小应变阶段采用ZWT黏弹性本构模型进行表征。作者对比分析了室温下HTPB/AP CBBG准静态压缩和拉伸力学性能的异同,建立了计入累积损伤的黏弹-黏塑本构模型以表征有限变形区间HTPB/AP CBBG的力学行为[10],并进一步开展了233～323 K下HTPB/AP CBBG准静态和冲击压缩力学性能研究,建立了考虑内应力和驱动应力的屈服应力模型[11]。

针对塑性形变、损伤发展等导致的无定形高聚物非线性力学特性的本构建模研究已成为国内外学者研究热点。宏观唯象理论便于根据实验结果引入变量及表达式,避免对复杂细观结构的变化进行度量,在描述材料本构行为时具有一定的优势。Abdel-Wahab等[12]提出了双层叠加式黏塑性本构模型,描述了有机玻璃拉伸和弯曲力学行为。Boyce等[13]、Cho[14]、Srivastava等[15]及Okereke等[16]认为无定形高聚物受载后的应力来自分子链段间和分子链整体网络两个层次,提出了各自的多链黏弹-黏塑性本构模型,表征了多种材料力学响应的率温相关性,实现了对著名BPA模型[17]的扩展。另一方面,作为宏观唯象理论重要分支的不可逆热力学通过引入内变量,规范不可逆系统的能量耗散必须满足的热力学基本原理,结合自由能函数和耗散势函数,确定内变量演化法则,阐述外部环境对系统状态的影响。张泷等[18]在分析岩石蠕变响应时,引入三组内变量,建立了黏弹-黏塑-损伤本构模型,分析了不同蠕变阶段材料的能量耗散特性。Wang等[19]结合聚碳酸酯准静态和冲击拉伸力学性能,构造了具有应变软化和应变硬化效应的弹-黏塑-损伤模型。Hund等[20]对比验证了分别包含Drucker-Prager屈服面、Raghave屈服面和具有Green/Gurson形式屈服面的弹-黏塑性本构模型在描述PC/ABS共混物准静态拉伸力学性能时均具有一定的合理性。Chen等[21]将耗散势表示为温度的函数,描述了沥青材料在不同温度下的压缩和拉伸蠕变力学特性。Balieu等[22]采用具有Perzyna形式的内变量演化法则,建立了描述颗粒填充高聚物在低-中应变率下压缩和拉伸力学行为的弹-黏塑-损伤本构模型。Onifade等[23]分析沥青混凝土的低温损伤特性时发现,损伤值随温度的降低而增加。

本文进行了宽泛温度及应变率下HTPB/AP CBBG拉伸力学性能测试实验。温度范围233～323 K,应变率范围8.3×10-5～8.3×10-1s-1、1 200～8 000 s-1。分析了HTPB/AP CBBG拉伸力学性能及损伤发展的温度和应变率效应。基于不可逆热力学框架建立了黏弹-黏塑-损伤本构模型,并结合该模型的计算结果讨论了HTPB/AP CBBG在不同工况下的损伤演化情况。

1 实验方案

1.1 试 件

HTPB/AP CBBG试件密度为1.54 g·cm-3, AP颗粒和HTPB基体质量比为73∶20。试件由辽阳庆阳特种化工集团制备。

1.2 准静态拉伸实验

为确保软试件与夹具的有效连接,设计了如图1(a)所示的连接件,材料为45钢。连接件粘接端的凹槽底面和壁面与试件端部粘接后,静置1周进行拉伸实验。粘接后的试件标距段长20 mm,直径为10 mm。夹具夹持连接件远离试件端,试件拉断时停止实验,如图1(b)所示。应变率包括8.3×10-5,8.3×10-3s-1及 8.3×10-1s-1,温度T包括室温(301 K)及233 K。试件在低温环境下保温1小时后进行实验。

图1 准静态拉伸实验试件及装置Fig.1 Specimen and setup for quasi-static tensile experiment

1.3 分离式霍普金森拉杆实验

采用图2(a)所示的分离式霍普金森拉杆(SHTB)系统进行HTPB/AP CBBG冲击加载实验。撞击杆、入射杆、透射杆长度分别为400、3 000、1 500 mm,直径均为14.5 mm。由于入射杆较长,为避免杆件屈曲对实验结果产生影响,入射杆材料为弹簧钢60Si2MnA(密度7 800 kg·m-3,杨氏模量206 GPa)。HTPB/AP CBBG为低波阻材料,为增强透射信号强度,透射杆材料为超硬铝7A04-T6(密度2810 kg·m-3,杨氏模量71 GPa),并使用高灵敏度系数的半导体应变片记录入射波、反射波和透射波波形。连接件结构与图1(a)相同,但远离试件端加工有螺纹。粘接后的试件标距段长5 mm,直径10 mm,如图2(b)所示。试件两端的弹簧钢和超硬铝连接件分别与入射杆和透射杆端部通过螺纹连接。

(1)

(2)

(3)

式中：εI(t)、εR(t)、εT(t)分别为入射波、反射波和透射波历史信号；E′、C0分别为入射杆杨氏模量和波速；E″、C1分别为透射杆杨氏模量和波速,A为杆件横截面积。

为加热和冷却连接至入射杆和透射杆的试件,设计了一种小型发热陶瓷高温箱和液氮低温箱。实验温度包括323 K、室温(301 K)、253 K和233 K。温控可靠性试验结果表明,升降温过程中在拉杆试件端形成的温度梯度未对一维应力波的传播产生影响,且箱内试件所在位置温度波动范围小于2 K。试件于箱内保温1小时后进行实验。实验中发现,无需对入射波进行整形便可实现常应变率加载,即加载的大部分时间内反射波呈现平台状。各工况下均进行三次有效实验,并取平均曲线表征HTPB/AP CBBG的力学性能。

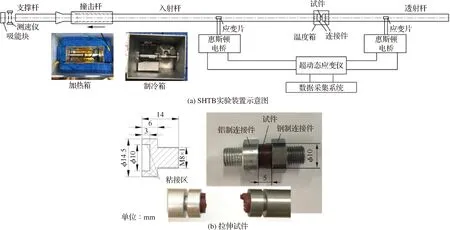
图2 SHTB实验装置示意图及试件Fig.2 Schematic diagrams of SHTB system setup and specimen

2 实验结果及分析

2.1 准静态拉伸力学性能

图3为准静态加载下HTPB/AP CBBG的σ-ε曲线。试件断裂前的一段应变区间内,材料应力骤降,试件内部损伤急剧发展,此时的损伤演化本质上为宏观裂纹扩展,属于断裂力学研究对象,这里不予讨论,故图3中σ-ε曲线保留至即将出现应力骤降的点,并将截取点应变记为εd。

图3表明,HTPB/AP CBBG准静态拉伸力学性能具有明显的温度敏感性和应变率增强效应。应变率越高,温度越低,初始模量E越高,εd越大。图4为σ-ε曲线的屈服点选取及区间划分示意图。301 K时,σ-ε曲线拐点为屈服点,初始弹性阶段,应力随应变增加而近似呈现线性增长,后屈服阶段呈现应变硬化特性,且应变率越高,应变硬化效应越显著。8.3×10-5s-1时,后屈服阶段呈现应力平台,此时试件形变缓慢,几乎处于平衡态,应变强化效应微弱,并在一定程度上被损伤引起的软化效应抵消。233 K时,σ-ε曲线峰值点为屈服点,初始弹性阶段,应力与应变亦呈现近似线性关系,后屈服阶段却出现应力降,表明损伤已占主导地位。由此可见,准静态拉伸载荷下,随着温度的降低,HTPB/AP CBBG细观结构破坏程度加剧,损伤趋于严重。

图3 HTPB/AP CBBG准静态拉伸力学性能Fig.3 Mechanical properties of HTPB/AP CBBG under quasi-static tension

图4 准静态加载σ-ε曲线屈服点及两区间划分示意图Fig.4 Schematic diagram of yield point and two regions of σ-ε curve under quasi-static loading

2.2 冲击拉伸力学性能

图5(a)为323 K时典型三波图,可见,反射波基本呈现平台状,加载应变率几乎恒定。由于入射杆与试件之间的螺纹连接导致反射波平台区间出现抖动,故此处通过对比F1=εIE′A-εTE″A和F2=-εRE′A判断动态应力平衡情况,如图5(b)所示。图5(b)表明,F1和F2基本吻合,试件达到了动态应力平衡,实验数据有效,可用于表征HTPB/AP CBBG的力学性能。

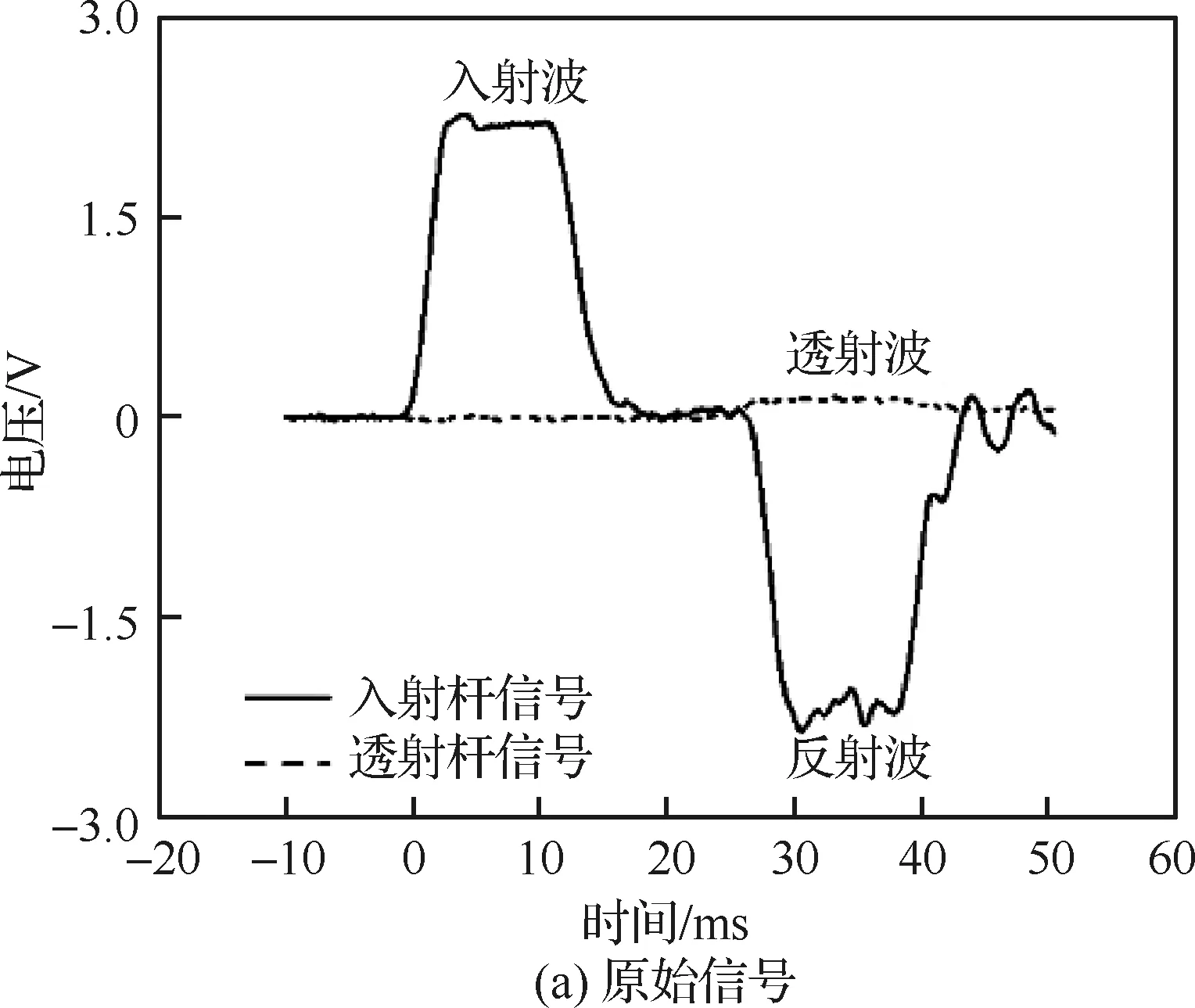
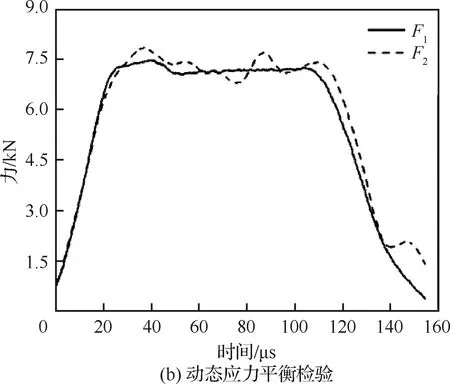
图5 SHTB实验典型数据Fig.5 Typical data in SHTB experiments

图6为冲击加载下HTPB/AP CBBG的σ-ε曲线。σ-ε曲线的屈服点选取和区间划分方法与准静态加载时相似,如图7所示。由于受加载波时长限制,SHTB实验尚无法获取试件加载至断裂的完整σ-ε曲线。图6表明,温度相同时,初始弹性阶段斜率基本重合,同时,冲击加载时HTPB/AP CBBG的力学性能与准静态加载时类似,当温度或应变率达到临界值时,后屈服阶段将由应变硬化转化为应变软化,出现应力降：323 K和301 K下应变率低于7 600～8 000 s-1时,后屈服阶段应力随应变增加而逐渐上升,若应变率继续增加,后屈服阶段应力随应变增加而逐渐下降；253 K和233 K下应变率为1 250～2 000 s-1时,HTPB/AP CBBG的应变硬化特征已经消失,应变率为4 650～5 000 s-1时,HTPB/AP CBBG力学性能呈现应变软化,可见,低温将降低导致软化效应的应变率值。

上述现象表明,在一定应变率范围内,随着应变的增加,损伤逐渐发展,当应变率高于临界值时,损伤将骤然增加,明显削弱材料强度,影响材料力学性能；另一方面,对于拉伸载荷而言,降低温度或增加应变率,HTPB/AP CBBG力学性能的韧脆转化现象显现。根据文献[11]提供的冲击压缩实验数据可知, 233～323 K下应变率为5 000～7 900 s-1时,HTPB/AP CBBG的力学性能曲线在应变为0.6以上时仍具有应变硬化特征。据此对比可知,冲击载荷下,HTPB/AP CBBG的抗拉强度明显低于抗压强度,大分子链及链段的物化交联作用力对拉伸载荷更敏感,这与文献[10]中提出的准静态载荷下HTPB/AP CBBG力学性能对加载方向的敏感性具有差异性的结论相吻合。

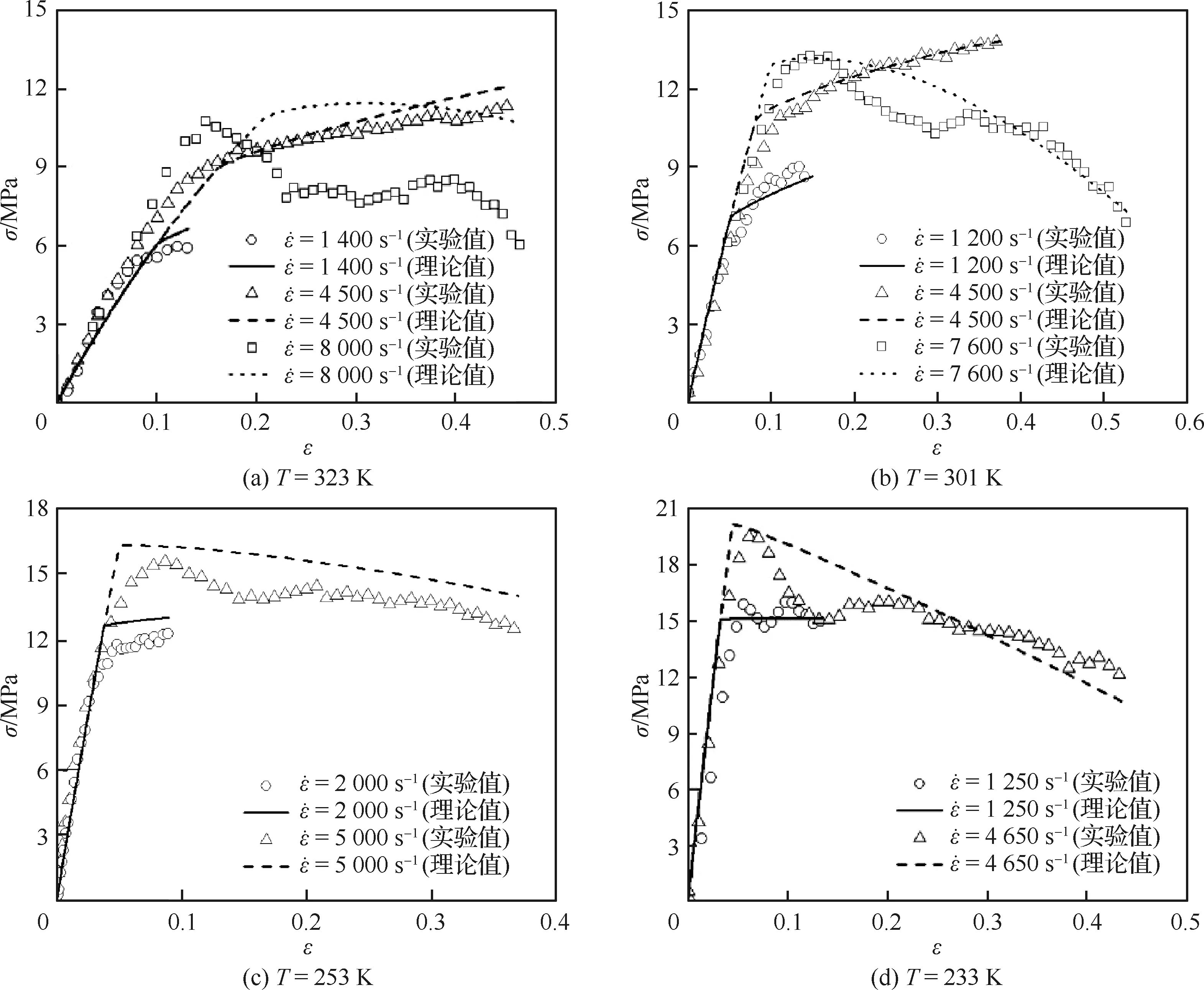
图6 HTPB/AP CBBG冲击拉伸力学性能Fig.6 Mechanical properties of HTPB/AP CBBG under impact tension

图7 冲击加载σ-ε曲线屈服点及两区间划分示意图Fig.7 Schematic diagram of yield point and two regions of σ-ε curve under impact loading

3 损伤本构模型

3.1 不可逆热力学框架

材料受载时发生的损伤扩展和塑性形变为不可逆的能量耗散过程,该过程必须满足热力学第一、第二定律。热力学第一定律的率形式为[24]

(4)

(5)

将式(4)代入式(5),并整理得

(6)

若忽略材料内部温度变化对材料力学性能的影响,式(6)简化为

(7)

假设ε、ψ均可分解为黏弹性部分与黏塑性部分,有ε=εve+εvp,ψ=ψve+ψvp。

假设屈服前,材料仅产生黏弹形变,且无损伤产生,屈服后,材料同时产生黏塑形变,并伴随损伤扩展,此时,损伤与黏弹性和黏塑性分别为状态耦合和动力耦合,即损伤与塑性相互促进和发展,损伤对材料刚度具有削弱作用,进而对弹性变形产生影响[25]。引入损伤内变量D和硬化内变量r,则有[25]

ψ(εve,D,r)=ψve(εve,D)+ψvp(r)

(8)

式(8)的全微分形式为

(9)

将式(9)代入式(7),并整理,得

(10)

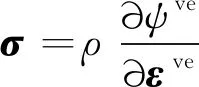
(11)

定义损伤耗散率

(12)

定义硬化应力

(13)

分别为与D、r共轭的热力学力,则式(10)表示为

(14)

假设耗散势φ的黏塑性部分φvp与损伤部分φd可以解耦,则有[25]

φ(σ,R,Y,D)=φvp(σ,R,D)+φd(Y,D)

(15)

则基于最小耗能原理[24],根据式(14)和式(15),可得内变量演化法则：

(16)

(17)

(18)

3.2 黏弹性模型

黏弹性材料与线弹性材料的主要区别是恒温恒应变率下,前者应力增量与应变增量之比并非定值,则可通过改进线弹性应力的方法,推导黏弹性应力。假设ψve具有线弹性材料Helmholtz自由能的形式,即

(19a)

(19b)

式中：σy为屈服应力。则根据式(11)和式(12),得

(20a)

(20b)

(21)

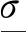
(22)

式中：B为材料参数。

图8为初始模量的温度及应变率敏感性。由图8可知,各温度下,冲击载荷下的初始模量较准静态载荷显著增加。准静态载荷下233 K时初始模量的应变率增强效应性明显高于301 K,而冲击载荷下,初始模量未表现出应变率效应(233 K下除外)。基于此,考虑对初始模量进行分段表征。准静态载荷下：

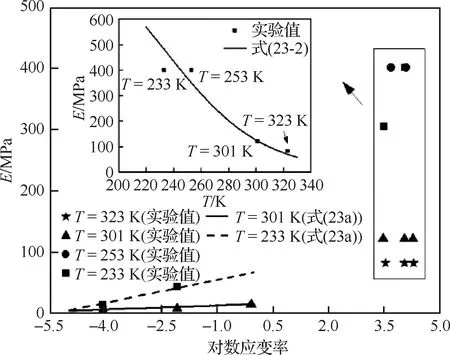
图8 初始模量与温度、应变率的相关性 (内图为冲击载荷下的初始模量,且不计应变率效应)Fig.8 Initial modulus as function of strain rate at different temperature (Inserted figures present initial modulus under impact loading with no strain rate effect.)

(23a)

冲击载荷下,忽略应变率效应,得

(23b)

表1 初始模量模型参数Table 1 Parameters for proposed initial modulus model

3.3 屈服应力模型

(24)

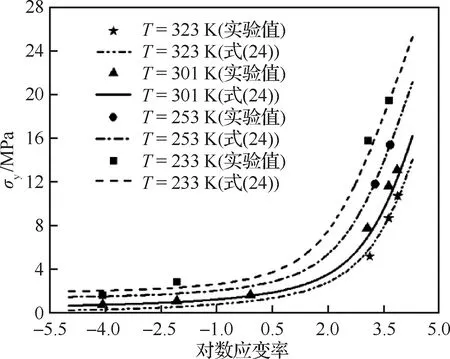
图9 屈服应力与温度、应变率的相关性Fig.9 Yield stress as function of strain rate at different temperature

表2 屈服应力模型参数Table 2 Parameters for proposed yield stress model

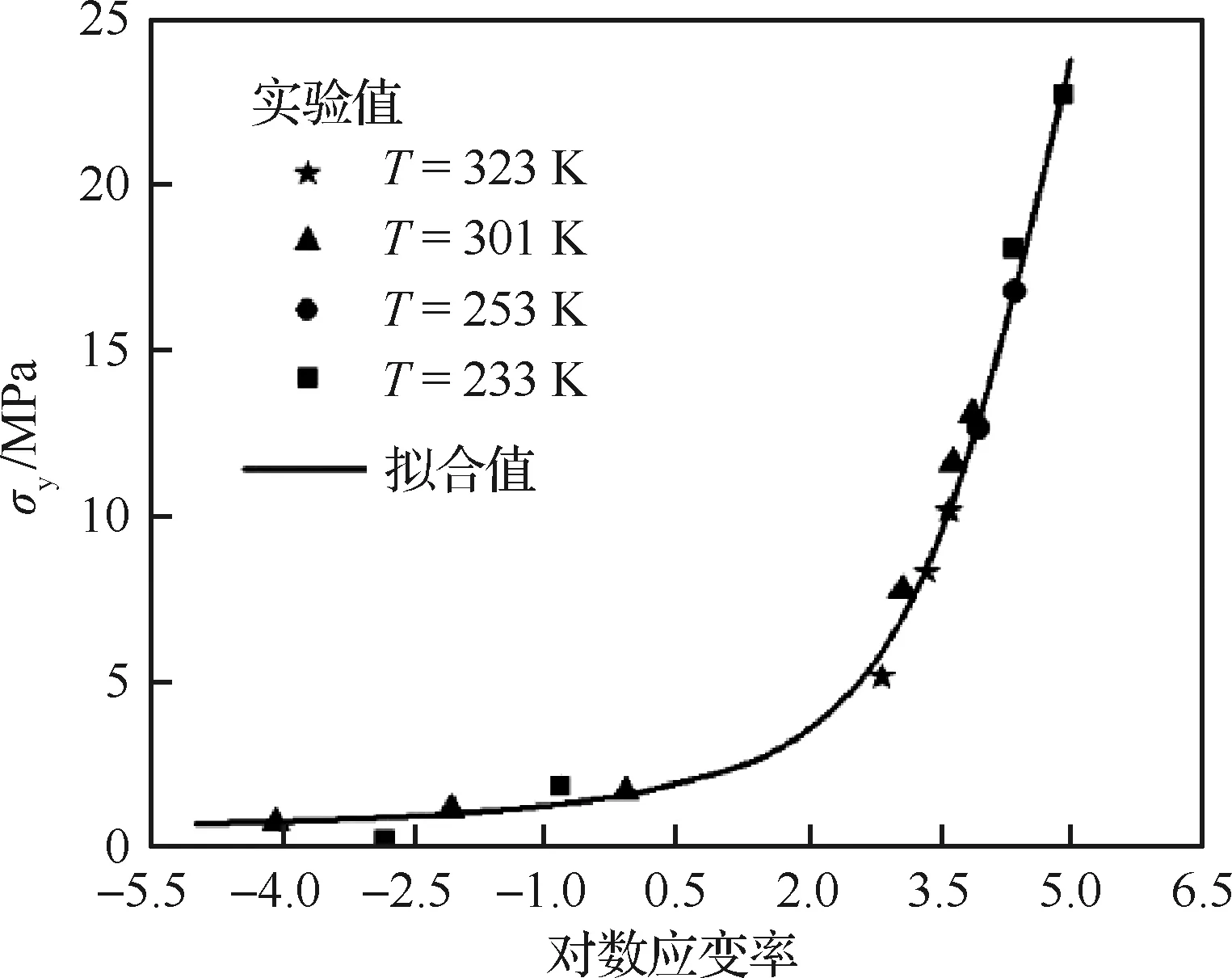
图10 参考温度为301 K时的屈服应力主曲线Fig.10 Master curve of yield stress built at reference temperature of 301 K

3.4 内变量演化律

定义

(25)

式中：K0、K1为材料参数,且K0为温度的函数。则由式(13)得：

R=K0rK1

(26)

采用关联流动法则,取塑性势面为屈服面F,即

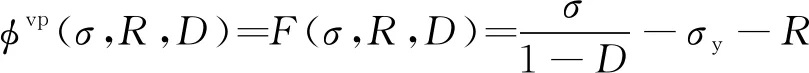
(27)

则分别根据式(16)和式(17)得

(28)

(29)

根据Perzyna提出的黏塑性本构理论[22,28],定义

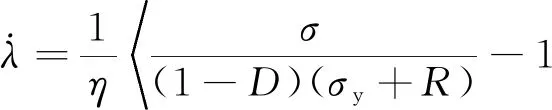
(30)

式中：η、g为材料参数；·为Macaulay括号,其满足的运算规则为：x>0时,x=x,x≤0时,x=0。

参考Lemaitre提出的损伤理论[25],定义

(31)

式中：S为材料参数,与温度和应变率相关。则根据式(18)得

(32)

3.5 结果及讨论

所建模型中,尚需拟合确定黏弹性参数B,硬化参数K0、K1,黏塑性参数η、g,损伤参数S。为便于求解S,引入参数Q和量纲归一化常数S0=1 MPa,并定义

(33)

则

S=10QS0

(34)

结合表1和表2中参数,根据301 K下8.3×10-5、8.3×10-3s-1及4 500 s-1时的σ-ε曲线,拟合参数B、η、g、K0、K1及Q,且不同应变率下Q的取值不同。利用B、η、g和K1拟合其他工况,得到对应的K0和Q。图11为各工况下K0、Q的拟合结果。图11表明,硬化效应随着温度的增加而增强,这与Al-Rub等[29]的结论一致,而Q值随着应变率的增加而逐渐增大并在2 000～4 000 s-1后陡然下降。

根据图11,考虑温度、应变率对材料参数的影响,分别采用和

(35)

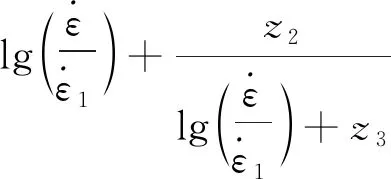
(36)

拟合K0和Q,P、T2、ϑ2、z1、T3、ϑ3、z2、z3为材料参数。至此,上述剩余模型参数已全部求出,如表3所示。拟合过程中发现,式(35)和式(36)各自多次拟合曲线基本相互吻合,各参数拟合值波动小,稳定性较高。

将表1～表3中的参数值代入损伤本构模型,得到各工况下σ-ε曲线的预测值。图3和图6将其与实验值进行了对比。总体来看,所建模型预测能力良好,可有效描述有限变形区间内,宽泛温度和应变率下HTPB/AP CBBG拉伸力学性能的黏弹性和后屈服阶段,模型合理。但室温下8.3×10-3s-1时的初始模量预测值误差偏大(误差为35.3%),233 K下准静态加载时的屈服应力预测值误差偏大(误差为18.3%～29.4%)323 K冲击加载时的初始模量预测值误差偏大(误差为18.8%)直接导致了此时σ-ε曲线预测效果较差。

文献[10]研究HTPB/AP CBBG的损伤特性时,基于累积损伤理论,给出了室温下8.3×

10-5～8.3×10-1s-1时的损伤因子f,表征经历损伤的削减作用后材料的剩余强度,即f=1-D,则文献[10]中的f-ε曲线可转化为D-ε曲线,图12将其与由本文模型计算的D-ε曲线进行了对比。由图12可知,本文损伤值随应变的增加而近似线性增长,这与文献[10]所述相同,且本文损伤最大值与文献[10]偏差在27.1%以内,表明两种损伤度量方法在一定程度上具有等效性。

图13为由所建本构模型确定的不同工况下损伤演化律,其清晰地揭示了损伤的温度和应变率相关性。由图13可知,同一温度下,准静态加载过渡到冲击加载过程中,损伤值随着应变率的增加先减小后增大,由此表明,中、低应变率范围内,提高应变率将抑制损伤发展,此时,损伤不能得到充分扩展。中、高应变率范围内提高应变率,损伤恶化,此时,短时间内在材料内部累积的大量能量有利于微裂纹萌生,特别是高应变率加载时,HTPB/AP CBBG在近似绝热环境中的黏性形变引起的热软化效应进一步促进微裂纹的发展,文献[30-31]已对此现象进行了研究。温度降低,HTPB/AP CBBG内分子链团运动能力下降,刚性增强,但承担有限拉伸形变的能力降低,损伤随之增长。表4对比了该增长趋势在准静态加载和冲击加载时的情况。表4表明,冲击加载下,低温导致的损伤增长更加显著,这从另一角度说明了冲击加载将促进损伤发展。

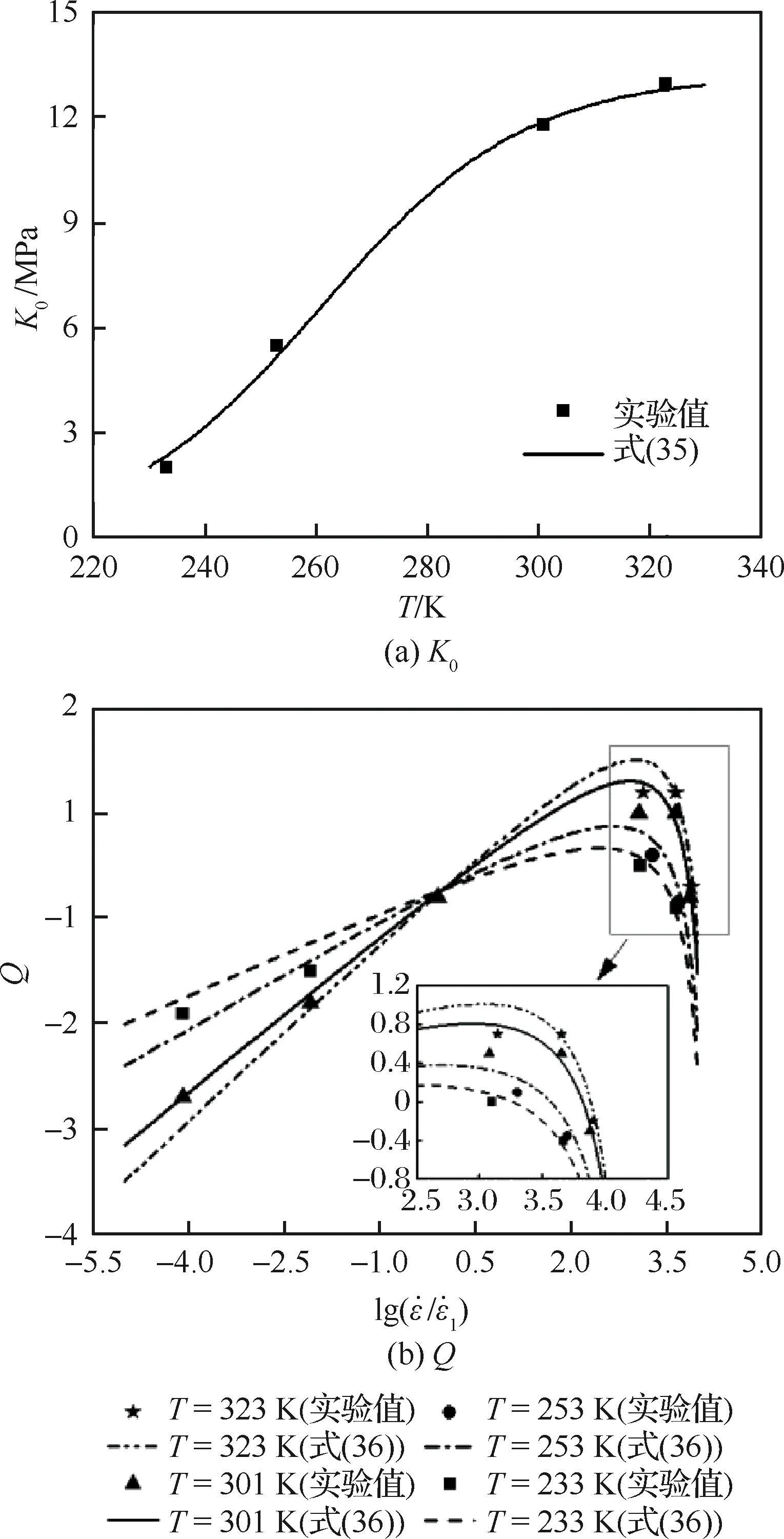
图11 不同材料参数随温度、应变率变化趋势Fig.11 Variation of material parameters with changes in temperature and strain rate

表3 材料参数Table 3 Material parameters

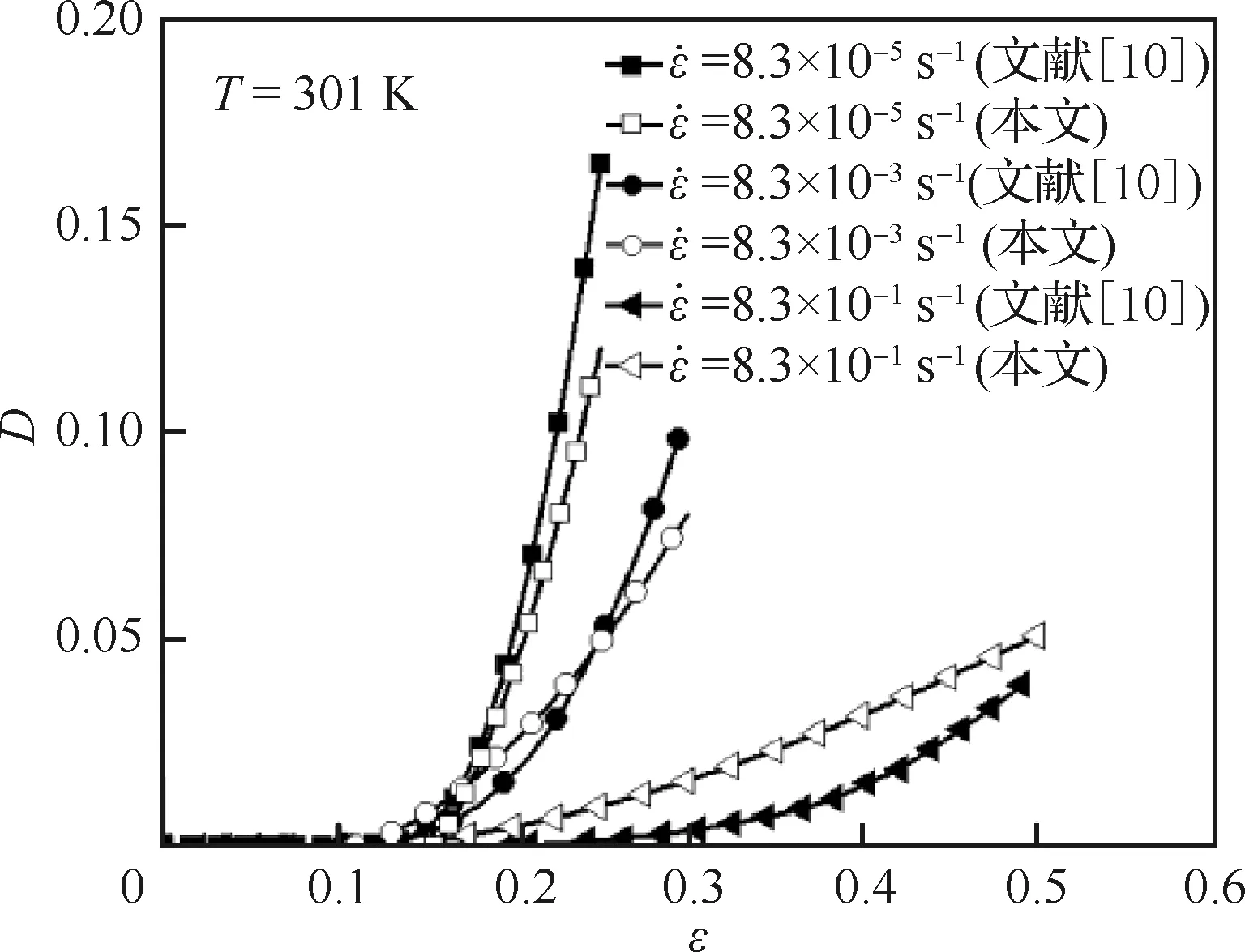
图12 本文确定的D-ε曲线与文献[10]的对比Fig.12 Comparison of D-ε curves identified in this study and that in Ref. [10]

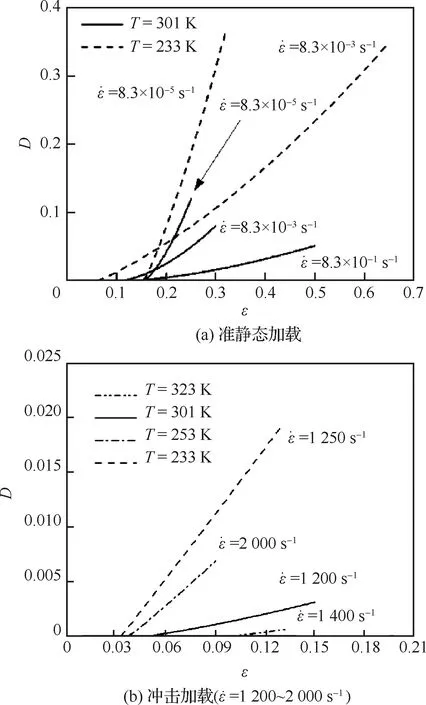
图13 损伤演化律Fig.13 Damage evolution

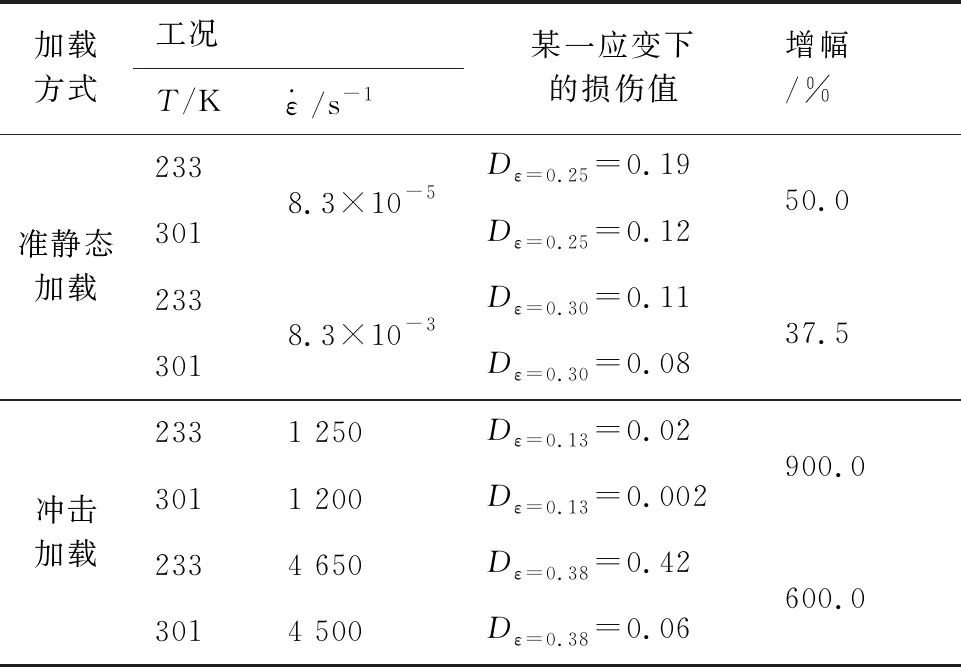
表4 不同工况下的损伤增幅Table 4 Damage increment under various loading conditions

4 结 论

1) 宽泛温度和应变率下,HTPB/AP CBBG单轴拉伸力学性能具有典型的非线性特征,屈服现象明显。

2) 准静态加载时,降低应变率,后屈服阶段应变硬化特征减弱；准静态加载时降低温度、冲击加载时提高应变率或降低温度,后屈服阶段由应变硬化转化为应变软化。这种形态的转变预示了损伤的增长,韧脆转化现象显现。

3) 通过将特定的Helmholtz自由能分解成黏弹性和黏塑性部分、耗散势分解黏塑性部分和损伤耗散部分,推导了与内变量共轭的热力学力表达式和内变量演化法则,并利用分段函数表征初始模量,利用改进协同模型表征屈服应力,在不可逆热力学框架下建立了HTPB/AP CBBG损伤本构模型,且模型对宽泛温度和应变率下材料的拉伸力学性能预测效果良好。

4) 应变硬化效应随着温度的升高而增强。应变率增加,损伤值先减小后增大,表明仅在一定范围内,增加应变率有利于抑制损伤发展。温度降低,刚性增加,但抵抗拉伸载荷能力降低,损伤值增大。