大跨域条件下的自适应滚转稳定容错控制方法
王雨辰,林德福,王伟,*,纪毅
1. 北京理工大学 宇航学院,北京 100081 2. 无人机自主控制技术北京重点实验室,北京 100081
弹体滚转引起的初始偏差角度影响弹药加速度指令的响应速度,弹药制导精度,甚至引起脱靶。当弹药执行大跨域飞行任务时,其飞行包络显著增大, 飞行速度、动压、攻角等实时大范围波动,气动扰动参数高频抖振,对弹药滚转通道的稳定性造成恶劣影响[1,2]。传统的滚转稳定控制设计基于经典控制理论,忽略模型中非线性项和不确定项,设计快速响应的滚转通道自动驾驶仪。Arrow和Williams[3]忽略系统的交叉耦合,针对滚转通道的线性模型设计了一种含有协调支路的自动驾驶仪。Kovach等[4]忽略三通道间的耦合,利用频率法和根轨迹法设计三通道自动驾驶仪,设计的驾驶仪响应迅速,能够快速跟踪控制指令。然而,采用古典控制方法需要进行大量的增益调度以克服气动参数的大幅度变化,控制方法繁琐,控制效率较低,难以适应大跨域环境。因此,亟需设计具有强鲁棒性的滚转通道控制方法。
随着控制理论的发展,现代控制方法逐渐被应用在自动驾驶仪的设计中[5],Williams和Friedland[6]提出了一种基于状态空间技术的线性二次高斯(LGQ)法,将滚转通道解耦到一个独立子系统,并在一定工作区间对模型进行线性化,完成自动驾驶仪的设计。彭博等[7]针对滚转弹耦合和传统增益调度设计中的缺陷,设计了一种基于BP神经网络的自适应调度算法,增强解耦效果,解决滚转弹药大空域飞行中的控制参数调度问题。Jin和Chwa[8]基于尾翼控制的弹药模型,提出了一种自适应的线性反馈控制方法。Rezazadeh等[9]提出了侧滑转弯(STT)控制弹药的滚转通道模型,并通过不确定性与扰动估计器(UDE)算法实时估计模型中的非线性时变气动参数,利用极点配置法设计了一种鲁棒解耦滚转驾驶仪。近年来,滑模变结构控制理论由于其显著的鲁棒性而得到重视并广泛应用于弹药控制系统的设计中。Shima等[10]将滑模控制理论应用到制导控制一体化系统设计中。Awad和Wang[11]基于扩张状态观测器,设计了一种终端滑模三通道稳定驾驶仪,补偿了气动参数非线性变化在整个飞行过程中的影响。王伟等[12]利用二阶滑模理论设计了一种强鲁棒性的滚转稳定控制器,控制弹药快速达到期望的滚转角速度,并进一步提出了一种基于super-twisiting算法的滚转稳定控制器,在控制滚转角速度快速收敛的同时抑制抖振。沈毅等[13]针对激光制导炸弹滚转控制通道的时变特性,通过状态反馈改善弹体动态特性,并在此基础上设计一种滑模变结构控制器,但对外部扰动的估计不足。
在工程实践中,积累性误差、突发性错误与指令饱和等执行机构失效情形时有发生,造成滚转失速失稳等不利影响,降低了执行机构的效率,甚至引发脱靶。为了提升弹药滚转通道的品质和可靠性,需要针对执行机构动力学与失效特性,对滚转通道进行容错控制设计。Xu等[14]基于带偏置项的Lyapunov函数设计了一种自适应控制算法,并通过反步法补偿未知执行机构失效。He和Lin[15]将执行机构失效视为模型不确定性,并通过设计滑模控制律控制视线角快速收敛,实现目标拦截。Wang等[16]通过假设执行机构失效为未知有界扰动,并设计状态扩张观测器(ESO)对扰动进行估计,通过反步设计实现三维制导控制一体化设计。Li等[17]通过状态观测器观测执行机构故障失效程度,建立容错控制器,提高弹药的鲁棒性。此外,执行机构的高阶动力学滞后特性是影响滚转通道响应速度的另一个重要因素,受到气动力及弹药自身硬件设备等因素的影响,弹药实际运动和控制指令之间存在一定延迟。因此,有必要在控制方法的设计中加入对弹药执行机构动力学滞后的补偿。Trivedi等[18]在考虑滚转通道二阶模型的同时,引入执行机构动力学滞后模型并考虑执行机构的输入饱和约束,通过滑模理论和反步设计补偿系统滞后,实现滚转通道快速响应和弹药的大攻角飞行。
受上述文献的启发,本文面向大跨域飞行条件下的制导弹药,针对其滚转通道中存在的非线性项和不确定项,以及执行机构故障失效问题,设计了一种自适应滑模变结构滚转稳定容错控制方法,相较于传统线性控制理论,本文提出方法能够有效控制滚转角和滚转角速度收敛到零,对气动非线性和不确定项具有强鲁棒性,提高制导弹药大跨域高攻角飞行的稳定性,并为提高末制导控制能力提供重要基础。另外,考虑执行机构失效现象,所设计控制方法能够补偿执行机构故障失效,提高控制可靠性。为了使设计更接近工程实际,本文进一步考虑执行机构动力学特性,采用反步设计(backstepping),在滑模控制方法的基础上设计一种反步控制方法,补偿执行机构动力学滞后对控制精度的影响。仿真实验表明,所设计控制方法具有强鲁棒性、快速性和有效性。
1 考虑执行机构故障的滚转通道动力学模型
弹药滚转通道动力学模型采用微分方程的形式可表示为
(1)
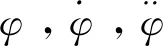

表1 参数定义及取值Table 1 Description and values of parameters
受文献[20]启发,本文提出一种基于参数自适应的滑模控制方法旨在解决大跨域、大攻角及机动飞行条件下,气动扰动参数剧烈变化,滚转通道的控制问题。另外,本文在后续章节考虑执行机构故障以及执行机构动力学滞后特性,得到基于参数自适应的反步控制方法。
考虑到执行机构故障失效现象,可以将舵偏角表示为
δa=fv+Δδ
(2)
式中:0.3≤f≤1为执行机构的故障失效系数;v为待设计控制方法;Δδ为模型误差。当f=1、Δδ=0时,表示未发生执行机构故障失效。定义u=δa,并引入执行机构失效模型(2),得到
u=fv+Δδ
(3)
(4)
式中:d2=Kαsin4x1+Δδ+d1。

至此,考虑执行机构失效的滚转通道控制模型建立完毕。
2 自适应容错控制方法设计
针对系统(4)设计滚转控制指令v。滑模控制方法设计包括滑模面的设计和趋近率的设计。考虑到快速终端滑模(FTSM)具有强鲁棒性,高精度和快速收敛的优点,选择,首先设计包含滚转角度和滚转角速度的快速终端滑模面
s=x2+αx1+β|x1|psgn(x1)
(5)
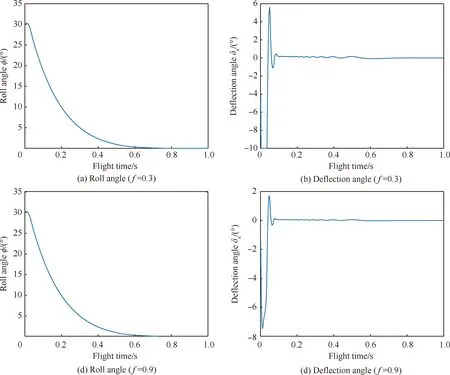
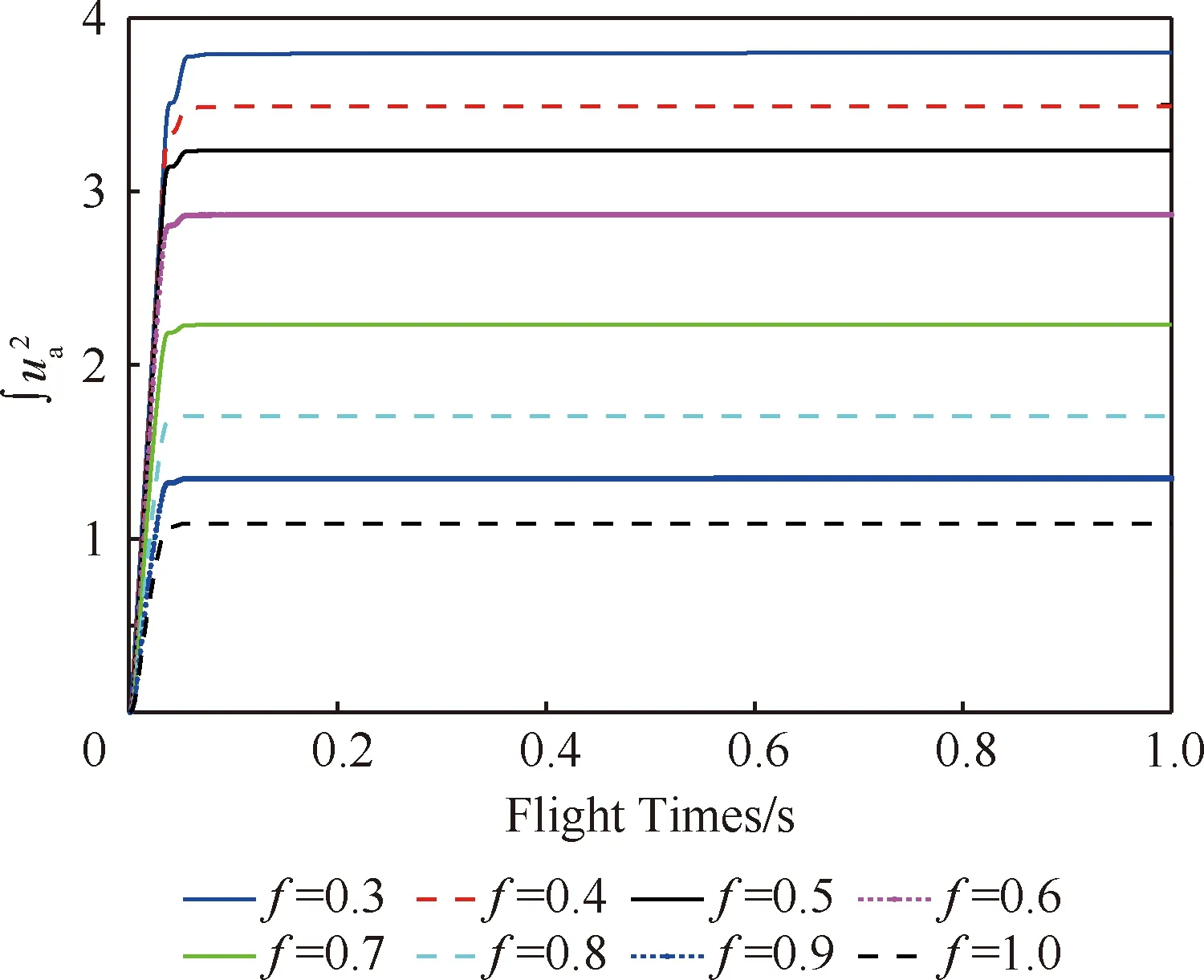
式中:α>0,β>0,1 对滑模面求一阶导数得到 (6) 式中:F=Kδf。 选取自适应滑模趋近率为 式中:Λ为设计参数;ρ(t)为表达式为 (8) (9) 综上,设计控制方法为 Λs-ρ(t)sgn(s))/F (10) 定理1针对滚转通道执行机构故障失效动力学系统(4),采用所设计控制方法(10),则系统中滚转角误差和滚转角速度能够在有限时间内收敛至滑模面s=0的下述邻域内, (11) (12) 将式(10)代入式(7)可以得到 (13) 为证明系统的稳定性,构造Lyapunov函数为 (14) 对式(14)求一阶导数得 (15) (16) 将式(16)代入(15)得 (17) 事实上 (18) 式(17)可以进一步化简为 (19) (20) 第2节采用理想执行机构假设,忽略执行机构动力学的影响。然而,在实际工程中,执行机构对执行机构指令的响应存在滞后,如果忽略其影响,会引起一定误差。因此,本节采用反步法设计控制方法,补偿执行机构动力学滞后。首先,执行机构动力学可视为一阶滞后环节,表示为 (21) (22) 注意到系统(22)呈现出严格反馈的形式,因此可利用传统的反步设计方法来设计执行机构指令uc,控制状态变量x1和x2在有限时间内收敛到零。 定义追踪误差z1=x2,并求其一阶导数得到 (23) 根据式(10),设计如下虚拟控制律: ρsgn(s))/F (24) (25) 对系统(25),设计指令舵偏角uc为 (26) 式中:l1>0,l2>0,0<γ<1为待设计参数。 (27) 定理2考虑系统(22),所设计指令舵偏角(26)能够控制状态变量x1、x2和x3在有限时间内收敛到一个零附近的小邻域。 引理如果存在正定Lyapunov函数及参数β1>0,β3>0及β2∈(0,1)满足: 则系统状态能够在有限时间内到达原点,且时间Tr满足: 式中:V(x0)为V(x)的初值。 (28) 根据引理,W1将在有限时间内收敛到零。同理,结合定理1,V2将会在有限时间内收敛到零附近的邻域,证明完毕。 本节通过设计考虑驾驶仪滞后约束系统及进一步考虑失效系统的仿真实验来验证所设计的自适应滑模控制方法的有效性和快速性。仿真参数如表2所示。 表2 设计参数Table 2 Design parameters 图1 不考虑执行机构动力学滞后的仿真结果Fig.1 Simulation results without actuator lag constraint 图1分别给出了扰动参数存在采用所设计控制方法得到的滚转角度、滚转角速度、舵偏角、滑模变量、自适应参数的变化和自适应参数对扰动估计的情况。图1(a)和图1(b)表明,滚转角和滚转角速度大致在0.7 s收敛到零,验证了所设计控制方法(10)的快速性,高精度的控制能力。另外,从图中可以看出,在不同飞行攻角条件下,滚转角和滚转角速度的收敛轨迹几乎重合,验证了设计控制方法的鲁棒性。从局部放大图可以看出收敛轨迹平滑,没有出现抖振现象,验证了控制方法良好的抑制抖振能力。图1(c)展示了滚转稳定控制过程中执行机构实际的偏转角度,其小于偏转角速的输入饱和限制,说明用于稳定滚转角度的控制资源较小,减少能量消耗。图1(d)展示了滑模面的有限时间收敛特性。自适应参数的变化情况如图1(e)所示,自适应参数在初期不断变化,迫使滚转角和滚转角速度的收敛。当系统进入收敛域后,自适应参数收敛,保证有界性。如图1(f)所示,ρ(t)可以实现对扰动变化趋势的跟踪,用于抵消扰动对系统的影响。 对比图1和图2的仿真结果,在气动扰动参数60%正向拉偏的情况下,仿真结果差异较小,进一步验证了所设计容错控制方法对气动参数非线性变化的鲁棒性。 综上,当存在执行机构动力学滞后时,所设计滑模自适应控制方法有效补偿执行机构动力学滞后,同时满足执行机构输入饱和限制,符合工程实际。 图3 考虑执行机构动力学滞后的仿真结果Fig.3 Simulation results with actuator lag constraint 本小节将所设计滑模自适应控制方法应用到故障失效系统中分别对控制力失效因数f=0.3和f=0.9的情况下进行仿真分析。以弹药保持16°飞行攻角为例,选择初始滚转角度为φ(0)= 30°。图4分别给出了2种不同失效因数情况下的仿真结果。当f=0.3时,由图4(a)和图4(b)可以看出,所设计容错控制方法(26)能够控制滚转角度在0.8 s收敛到零,在执行机构失效的情况下仍使滚转角快速收敛,执行机构偏转角度满足输入饱和限制。当f=0.9时,由图4(c)可知滚转角约在0.7 s收敛到零,且执行机构偏转角度满足输入饱和限制(图4(d))。对比不同失效因数下的执行机构偏转角度,当失效严重时,执行机构增大偏转角度来弥补执行机构控制效率降低的影响。针对不同失效因数下的滚转通道进行的故障仿真说明,所设计容错控制方法能够实现在执行机构失效情况下滚转角的快速收敛。 图4 f=0.3和f=0.9的故障系统Fig.4 Actuator fault system with f=0.3 and f=0.9 图5给出了不同失效因数下的控制能量变化情况。对比发现,失效严重(即f减小)的情况下,为实现滚转稳定,需要执行机构提供更多控制能量。 图5 控制能量Fig.5 Control effort 1) 本文首先提出了一种基于自适应滑模控制理论的滚转稳定容错控制方法,所设计方法具有较强鲁棒性,通过气动参数拉偏仿真实验,验证了所设计控制方法对气动参数的不敏感性。设计方法保证闭环系统的稳定性和跟踪性能。对比分析了执行机构在不同失效程度下,所设计控制方法对滚转通道的控制能力,有效提高了滚转通道的稳定性。 2) 进一步考虑执行机构动力学滞后特性,使设计更接近工程实际。仿真结果表明,所设计控制方法能够有效补偿执行机构失效及执行机构动力学滞后,提高弹药对控制指令的响应速度,为后续提高弹药制导精度提供基础。
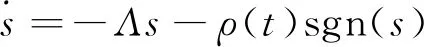



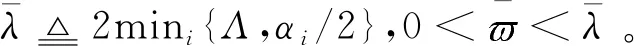

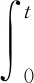




3 考虑执行机构动力学特性的滚转控制方法设计


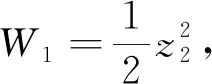
4 仿真分析

4.1 不考虑驾驶仪动力学的容错滚转稳定控制方法
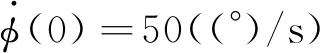


4.2 考虑驾驶仪动力学的容错滚转稳定控制方法
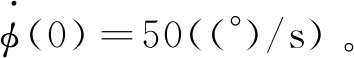



4.3 考虑失效系统的自适应滑模控制方法仿真
5 结 论

