Maxwell气固相互作用模型对稀薄高超声速凹腔绕流流动特征和热环境的影响

靳旭红,黄飞,程晓丽,苏鹏辉,*

1. 中国航天空气动力技术研究院,北京 100074 2. 清华大学 航天航空学院,北京 100084 3. 中国航天科技集团有限公司 航天飞行器气动热防护实验室,北京 100074

航天器再入过程之初,速度通常高达数十千米每秒。因此,在再入过程中,航天器与地球大气产生剧烈的摩擦,一方面使其速度降低到着落速度,另一方面却导致其外表面温度高达1 700 K,这个温度远远超过不锈钢的熔点[1]。因此,为了保护航天器外部表面和内部设备,热防护系统至关重要。比如,航天飞机表面一般都覆盖了超过32 000片防热瓦,这些防热瓦通常以对齐或者交错的方式相连,不可避免地产生了防热瓦缝隙[2]。

此外,制造公差、传感器安装、非相似材料的不均匀膨胀或烧蚀等诸多原因也会导致航天器表面存在缝隙和缺陷等凹腔结构[3]。航天器表面凹腔结构的存在会影响其流动状态和传热特性：首先,凹腔入口处产生边界层分离和再附,导致局部热流升高；其次,凹腔干扰可增加湍流度,促进边界层转捩,导致整个表面的热流增加；最后,由于凹腔狭小,辐射散热效应被阻塞,即使凹腔内热流很低,也可能产生较高的凹腔表面温度[4]。因此,表面凹腔的存在对局部热防护系统会产生重要的影响,甚至导致局部防热结构的破坏[5]。

然而,在热防护系统热载荷的计算和分析中,出于简化问题的考虑,通常假设航天器具有光滑连续的表面。根据哥伦比亚航天飞机事故调查委员会(Columbia Accident Investigation Board,CAIB)的调查结果,造成哥伦比亚航天飞机坠毁事故最可能的原因是左部机翼前缘热防护结构的破裂,致使机翼直接暴露于高速高能气流中[6]。该调查结果不但得到了美国国家航空航天局事故调查组(NASA Accident Investigation Team,NAIT)的支持,同时还表明了再入条件下热防护表面凹腔结构绕流的复杂性和对其展开研究的必要性。

对于连续流区的高速凹腔绕流问题,前人在实验和计算方面都做过大量的研究[3-4,7-11],Lawson和Barakos[12]在其综述文章中做了比较全面的介绍。

早期的研究发现凹腔流动特征与凹腔入口处的速度和凹腔几何形状息息相关,几何形状主要通过凹腔长深比(长度与深度之比,L/D)表征[12]。一般而言,凹腔绕流分成3种模式：开式、闭式和过渡式[9]。对于高速凹腔绕流,长度较小而深度较大的凹腔通常为开式凹腔,长度较大而深度较小的凹腔为闭式凹腔。一般情况下,长深比小于10的凹腔为开式,长深比大于13的凹腔为闭式,上述两类流动之间的中间状态称为过渡式凹腔流动,其长深比为10～13[10]。需要注意的是,上述凹腔流动模式的界限只是名义上的,仅仅具有指导意义,因为不同研究者测量得到的界限实际上是一个范围,开式凹腔长深比的上边界为9～11,闭式凹腔长深比的下边界为12～15[11]。

对于开式凹腔绕流,外部主流在凹腔前缘分离,外部主流和凹腔之间形成的剪切层横跨整个凹腔,并附着到凹腔后缘,在凹腔内部形成一个单涡结构[7]。对于闭式凹腔,外部主流在凹腔前缘分离后,没有足够的能量跨越整个凹腔,最终附着在凹腔底面；流动再次在凹腔底面分离,并再次附着到凹腔后缘,在凹腔内部形成了双涡结构[8]。过渡式凹腔兼具开式和闭式凹腔的部分特点,一般不太稳定,在一定条件下容易向开式或闭式凹腔转化[4]。

关于凹腔热环境方面的研究,邱波等[13]通过求解可压缩的Navier-Stokes(N-S)方程,对横缝流场结构和热流分布进行了数值模拟,发现缝隙壁面上形成了多个局部高热流区；同时,他们还研究了来流马赫数、雷诺数和攻角等对防热瓦横缝旋涡结构及热环境的影响。

然而,几乎所有高超声速凹腔绕流的研究都只考虑连续流区的层流和湍流,而涉及临近空间稀薄流区凹腔绕流现象的研究较少[14]。考虑到航天飞机等可重复飞行器再入时在高空仍然面临严峻的热防护挑战,Palharini等[15-16]采用直接模拟Monte Carlo(Direct Simulation Monte Carlo,DSMC)方法研究了80 km高度稀薄流区高超声速凹腔绕流问题,探索凹腔长深比对凹腔内部流场结构、壁面压力和热流的影响规律；他们发现稀薄过渡流区几何尺寸对高超声速凹腔绕流的影响与连续流区存在不同,主要表现为当长深比等于4时凹腔内部就出现了双涡结构和剪切层在凹腔底面再附,而连续流区产生类似现象对应的长深比为14。Paolicchi和Santos[17]也进行了类似的研究,只不过他们考虑的凹腔更深。靳旭红等[18]采用DSMC方法对稀薄流区高超声速凹腔绕流问题进行了数值模拟,研究了稀薄气体效应和三维效应对凹腔内部流场结构和壁面热流的影响规律。Guo和Luo[19]同样采用DSMC方法研究了一系列凹腔绕流流场特征,他们的来流条件覆盖了从近连续流到稀薄流的宽流域。

在现有的稀薄高超声速凹腔绕流研究中,气固相互作用(Gas-Surface Interaction,GSI)模型均为完全漫反射模型,国内外的研究人员尚未考虑过GSI模型对凹腔绕流的影响。然而,大多数稀薄流问题都涉及气固相互作用,因为气固相互作用模型为稀薄流的理论分析和数值模拟提供适当的边界条件[20]。稀薄流中速度滑移和温度跳跃大小就与气固相互作用息息相关[21]。而且,由于凹腔的存在,流场的表面积与体积之比变大,气固相互作用的影响更为明显[22]。

本文在前人研究的基础上,采用DSMC方法对稀薄高超声速三维凹腔绕流问题进行模拟,考虑气固相互作用模型对凹腔流动特征和气动表面量(表面压力和热流)的影响,探索流动特征、表面压力和热流随着GSI模型的变化规律,并从气体动理论的角度阐明其作用机理,为航天飞机等可重复飞行器的热防护系统精细化设计提供数据支持。

1 气固相互作用模型

气固相互作用的研究介于气体动理论与固体物理之间,历史上,第一个GSI模型由Maxwell提出,这就是著名的Maxwell气固相互作用模型,也称为Maxwell边界条件[23]。Maxwell模型考虑了两类相互作用：镜面反射和漫反射。

当气体分子发生镜面反射时,其切向速度分量保持不变,而法向速度分量反向。因此,入射角等于反射角,反射前后气体分子的动能不变。令入射分子的速度为ci,固体表面单位外法向量为n,则反射后的速度cr为

cr=ci-2(n·ci)n

(1)

当气体分子发生漫反射时,反射后的速度服从基于固体表面温度Tw的Maxwell分布。在径向为表面外法向的局部球坐标系中,反射分子的速度为

(2)

式中：cr为反射速度cr的大小；cw为基于表面温度Tw的最概然热运动速率；Ri(1 ≤i≤ 4)为均匀分布于区间(0, 1)的随机数；θ和φ分别为该球坐标系中的仰角和方位角。

Maxwell气固相互作用模型为完全漫反射和镜面反射的加权平均,即σ部分的入射分子发生漫反射,剩下的1-σ部分反生镜面反射,其中σ称为Maxwell适应系数[23]。

1971年,Cercignani和Lampis[24]提出一种新的GSI模型,并由Lord[25]在DSMC中实现,这就是所谓的Cercignani-Lampis-Lord(CLL)模型。CLL模型满足互易性原理,通过引入对应的适应系数,考虑了气体分子切向动量和法向能量在固体表面的适应程度,并且能复现高速稀薄流条件下的实验结果。Padilla和Boyd[26]采用平板模型,通过对比速度分布、边界层形状和气动表面量,对Maxwell模型和CLL模型做了评估,发现当气体分子对表面的适应程度高于50%时,Maxwell模型和CLL模型给出的边界层形状和气动表面量类似。

在Maxwell模型和CLL模型之后,虽然又有多种GSI模型相继被提出,但稀薄高超声速来流条件下气体与固体表面相互作用中的基础物理和化学过程仍然几乎未知。在这种情况下,研究GSI模型对流动特征的影响,并评估气动表面量对GSI模型参数的敏感性尤其具有指导意义。由于Maxwell模型在稀薄气体动力学研究中应用最为广泛,加之其具有简洁的形式且满足互易性原理,本文通过改变Maxwell适应系数σ,采用参数化研究的手段评估气固相互作用对稀薄高超声速凹腔绕流流动特征和气动表面量的影响。

2 计算方法

2.1 DSMC方法

目前,稀薄气体流动最为广泛使用的计算方法是由Bird[27]提出的DSMC方法,其前提是稀疏气体假设,即气体分子之间的距离远大于其直径。基于这个假设,气体分子运动和碰撞实现解耦。已经证明,当仿真分子数趋于无穷大时,DSMC收敛到稀薄气体动力学的Boltzmann方程[28]。

DSMC方法通过模拟大量仿真分子实现对气体流动的计算。每一个仿真分子都代表大量真实气体分子,并具有位置、速度和内能等属性。随着模拟过程的进行,通过跟踪仿真分子的轨迹、计算仿真分子之间的碰撞以及仿真分子和固体表面之间的相互作用,仿真分子的信息不断更新[29]。跟踪足够多的时间步以保证流场收敛且统计误差足够小之后,统计出流场宏观量(速度、温度及压力场等)和气动表面量(表面压力及热流等)。

基于DSMC方法,课题组自主开发了一套通用的三维并行稀薄气体流动分析软件,其核心计算模块为一套非结构网格DSMC程序,并已成功应用于大量工程问题。在该DSMC软件中,气体分子模型为变径硬球(Variable Hard Sphere,VHS)模型[23],气体分子之间的碰撞采用非时间计数(No Time Counter,NTC)采样技术[23],气体分子之间的内能交换采用Larsen-Borgnakke模型[30]。

2.2 亚松弛采样技术

由于凹腔内部局部为低速流动,采用了孙泉华和Boyd[31]提出的宏观量亚松弛采样技术,通过引入松弛因子,等效地增加了采样数量,有效地降低了DSMC方法模拟低速流动宏观量计算的统计误差。亚松弛采样技术已被证明对局部为低速流动的问题(比如凹腔绕流和管道流动等问题)特别有用。定常流动的亚松弛宏观量采样技术通过如下过程实现[31]：

首先,基于初始条件,实现宏观量的初始化估计,表示为A0。

(3)

最后,增加校正步以消除初始条件和较早时间步瞬时值引入的误差,即

(4)

3 物理模型

3.1 研究对象

考察带有凹腔的三维平板模型,如图1所示。凹腔长度为L,深度为D,宽度为W,凹腔上游的平板长度为Lu,下游长度为Ld,平板宽度为Wp。坐标原点位于平板凹腔几何中心在平板表面的投影点,x轴沿流向为正,y轴垂直向上为正,z轴由右手法则确定。

需要注意的是,本文考虑的凹腔尺寸代表了典型的防热瓦缝隙尺寸和航天器表面的缺陷尺寸,为了进行验证,这些尺寸和文献[14]中的一致。此外,为了深入研究GSI模型的影响,排除凹腔几何因素的干扰,仅仅考虑长深比L/D= 1的情形。为便于下文分析,把凹腔的上游壁面表示为FW,其位置xFW=-1.5 mm,凹腔底面表示为CF,其位置yCF=-3.0 mm,下游壁面AW,其位置为xAW= 1.5 mm。

图1 带有凹腔的平板示意图Fig.1 Schematic drawing of flat plate with cavity

3.2 来流及计算参数

考虑80 km高度的大气环境,来流大气为体积比例为76.3%的N2和23.7%的O2,来流马赫数Ma∞=26.77,攻角α= 0°,来流温度T∞、压力p∞和密度ρ∞采用美国标准大气(1976)确定,来流速度u∞由来流马赫数Ma∞确定,具体的来流参数列于表1中。平板及凹腔表面为完全漫反射表面,其温度均保持为1 000 K,接近再入飞行器驻点附近的温度。取凹腔长度为特征长度,则对应的来流Reynolds数和Knudsen数分别为Re∞=126.875和Kn∞=0.367,表明该凹腔绕流问题是一个稀薄过渡流区的高超声速层流问题。

表1 自由来流条件Table 1 Free-stream parameters

4 方法验证和确认

准确DSMC需要网格尺寸不大于当地分子平均自由程,也要求时间步长不大于当地分子平均碰撞时间。此外,为了降低统计误差,单个网格单元内部的仿真分子数也应足够多。因此,设计一系列算例对研究方法进行验证和确认,涉及所有算例的GSI模型均为完全漫反射模型,即Maxwell适应系数σ= 1.00。

4.1 方法验证和网格尺寸

为进行网格无关性研究,设计3套网格(稀疏、标准和稠密网格),网格单元数分别为544 040、4 330 480和14 640 000。每套网格均为非均匀网格,在平板和凹腔附近实施了局部加密。令表面压力和热流为p和q,则表面压力和传热系数的定义为

(5)

图2为采用上述3套网格计算出的凹腔下游壁面(AW)中心线上的表面压力和传热系数分布,同时还给出了Palharini等[14]的计算结果。显然,无论是表面压力系数还是传热系数,本文结果与Palharini等[14]的结果都比较一致,表明课题组发展的DSMC软件能准确预测表面压力和热流等宏观量,具备可靠性。此外,稀疏、标准和稠密网格给出的压力和热流几乎都没有变化,确认了计算结果的网格无关性。

图2 方法验证和网格无关性确认Fig.2 Method validation and grid-independence verification

4.2 时间步长

为进行时间步长无关性研究,采用3个时间步长(Δt= 1.5×10-8s, 1.0×10-8s, 0.5×10-8s)计算,其中Δt= 1.0×10-8s为标准时间步长。需要注意的是,上述3个时间步长均远远小于基于来流条件的分子平均碰撞时间,也小于当地网格尺寸与仿真分子速率的比值。

采用上述3个时间步长计算出的凹腔下游壁面中心线上的表面压力和传热系数分布如图3所示。显然,无论是表面压力系数还是传热系数,上述3个时间步长给出的结果几乎没有变化,确认了计算结果的时间步长无关性。

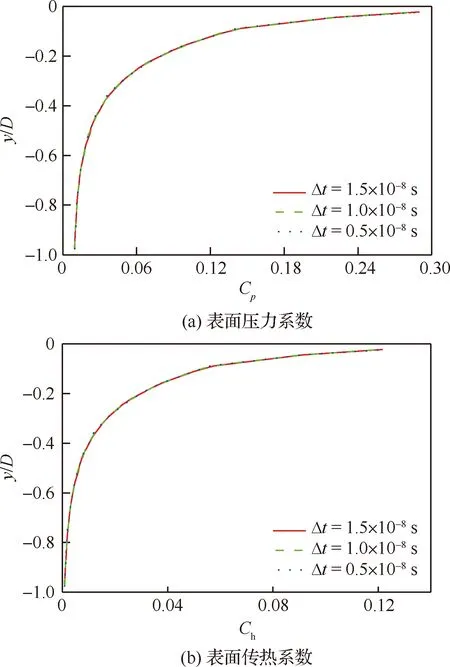
图3 时间步长无关性确认Fig.3 Verification for independence of time step

4.3 仿真分子数

为进行仿真分子数无关性研究,采用3个仿真分子数(Particle Per Cell(PPC) = 40, 80, 120,PPC表示每个网格单元的平均仿真分子数)计算,其中PPC = 80为标准仿真分子数。

图4为采用上述3套网格计算出的凹腔下游壁面中心线上的表面压力和传热系数分布。显然,无论是表面压力系数还是传热系数,上述3个仿真分子数给出的结果几乎都没有变化,确认了计算结果的仿真分子数无关性。

图4 网格单元仿真分子数无关性确认Fig.4 Verification for independence of average number of simulation particles in each cell

5 流场特征

图5为不同Maxwell适应系数给出的对称面上凹腔内部的无量纲密度(当地密度ρ与来流密度之比,ρ*=ρ/ρ∞)等值线和流线图。由图5可见,当σ=1.00时,即GSI为完全漫反射时,外部流动直接绕过凹腔,在凹腔前缘分离的剪切层再次附着在凹腔后缘,在凹腔内部形成一个充满腔体的单涡结构,分离点附近出现局部低密度区,再附点附近则出现局部高密度区域。

但是,随着σ的减少(漫反射的比例逐渐降低),凹腔内部流场特征和密度分布出现了一些变化。比如,涡结构不再充满整个凹腔,而是向凹腔左上角移动,涡形状也随之变化；当GSI为纯镜面反射时,涡结构完全消失,凹腔底部基本不存在流动,成为所谓的“死水区”。同时,凹腔后缘的再附现象逐渐消失,表现为后缘附近的高密度区逐渐缩小甚至消失。此外,凹腔内部的密度也逐渐减小：GSI模型为完全漫反射时,凹腔再附点附近区域的密度均大于来流密度,其他区域的密度则与来流密度相当；当σ减小到0.75时,再附点高密度区域面积减小的同时,峰值密度亦降低；当σ进一步减小到0.50(即一半漫反射一般镜面反射)时,在再附点高密度区面积进一步缩小和峰值密度继续减小的同时,凹腔内部大部分区域的密度均低于来流密度；σ=0.25时,再附现象及其引起的局部高密度区完全消失；σ=0,即GSI为纯镜面反射时,凹腔内部的密度呈现分层分布,底部出现了“死水区”。

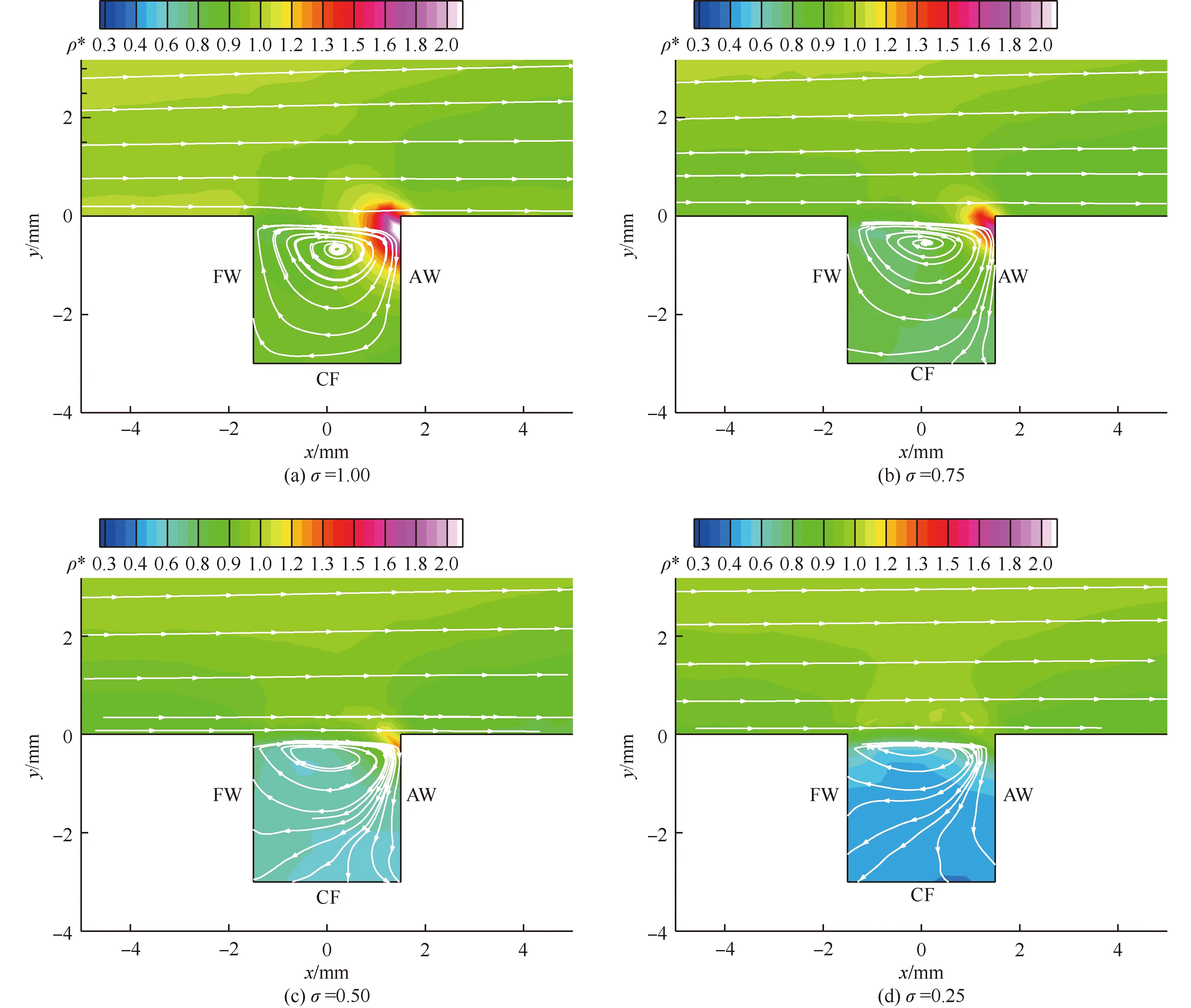
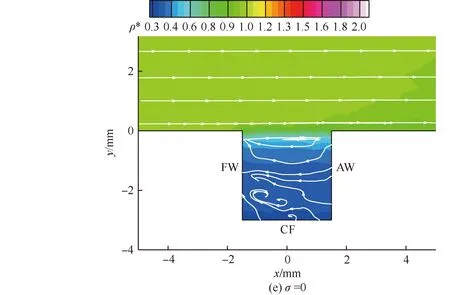
图5 对称面凹腔内部无量纲密度ρ/ρ∞等值线及流场结构Fig.5 Density ratio contours ρ/ρ∞ with streamline traces inside cavity on symmetric plane

上述流场特征和密度分布随着Maxwell适应系数σ的变化与气体分子和凹腔表面之间的剪切作用息息相关。随着σ的减小,气体分子与凹腔表面之间的切向动量交换减弱,即黏性作用减弱,导致外部气流被卷入凹腔内部的程度减弱。GSI为完全漫反射(σ=1.00)时,由于黏性剪切作用较强,在凹腔前缘分离的剪切层在后缘发生再附之后,一部分气流沿着凹腔下游壁面被卷入凹腔内部,使得凹腔内部的密度较大的同时,还形成一个饱满的涡结构。随着σ的减小,GSI从完全漫反射向纯镜面反射变化,气体分子与平板之间的黏性剪切作用减弱,凹腔顶部的剪切层逐渐消失,凹腔后缘的再附现象也随之减弱甚至消失,外流流动与凹腔之间的相互干扰仅仅作用在凹腔顶部区域,导致凹腔内部的密度逐渐减小,涡结构也逐渐消失。

6 表面压力和热流

6.1 表面压力

图6是不同Maxwell适应系数给出的3个凹腔表面中心线压力的分布,图中的pfp表示GSI为完全漫反射时对应平板附着流动(没有凹腔的情形)的表面压力,取值为12.48 Pa。

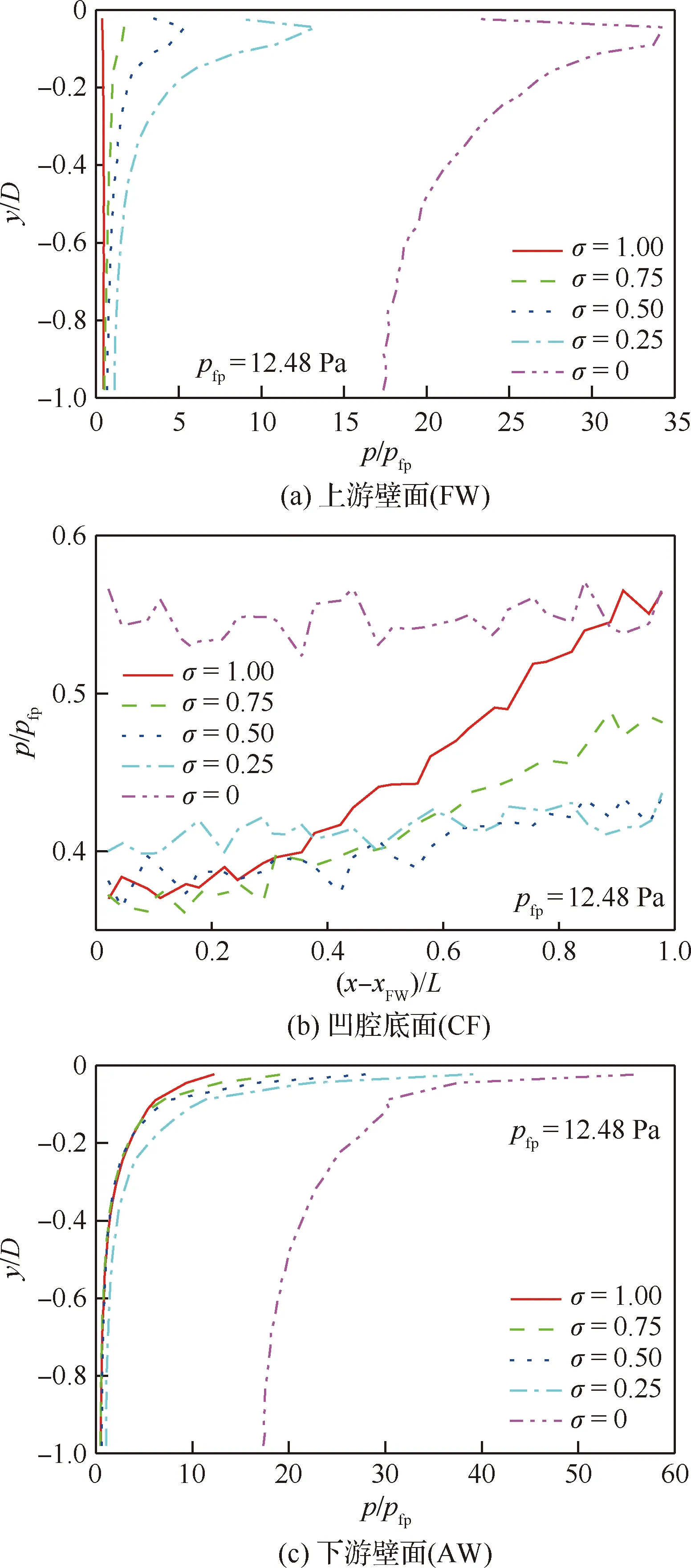
图6 不同GSI模型对应的凹腔表面中心线表面压力分布Fig.6 Distributions of surface pressure along centerlines of cavity surfaces for different GSI models

沿着凹腔上游壁面(FW),不同Maxwell适应系数对应的压力分布表现出相似性：压力在FW顶部较低,沿着FW向下逐渐增大,并在y/D=-0.05 处达到峰值,此后一致单调降低直至FW底部。GSI模型对FW的压力分布影响颇为明显：GSI从完全漫反射变化为纯镜面反射时,FW表面压力逐渐增大。具体而言,σ=1.00, 0.75, 0.50, 0.25, 0对应的FW压力峰值与平板压力的比值分别为0.48、1.69、5.37、13.27和34.29,非完全漫反射给出的FW压力峰值均大于对应平板压力,而且镜面反射的峰值压力是漫反射的70余倍,明显强调了FW峰值压力分布对于GSI模型的敏感性。

相对于平板压力值pfp,凹腔底面(CF)的压力都较低。随着GSI从完全漫反射变化为纯镜面反射,由于外部流动被卷入凹腔的程度减弱,涡结构逐渐消失,底部演变为“死水区”,故压力沿着CF的分布逐渐变得均匀。

不同Maxwell适应系数对应的凹腔下游壁面(AW)的压力分布也呈现类似性：压力在AW底部较低,此后沿着AW向上直至凹腔后缘一直单调增大。同样,AW的压力分布对GSI模型也特别敏感：随着GSI从完全漫反射变化为纯镜面反射,AW表面压力逐渐增大。具体而言,σ=1.00, 0.75, 0.50, 0.25, 0对应的AW压力峰值与平板压力的比值分别为12.25、19.49、28.15、39.00和56.37,均大于对应的平板压力,镜面反射的峰值压力是漫反射的4倍多。

在飞行器气动设计中,如果航天器或者防热瓦表面比较光滑或飞行速度较快导致一部分气体分子在其表面发生镜面反射时,需要特别注意表面缺陷或缝隙上游壁面和下游壁面的压力载荷。

6.2 表面热流

图7为不同Maxwell适应系数给出的3个凹腔表面中心线压力的分布,图中的qfp表示GSI为完全漫反射时对应平板附着流动(没有凹腔的情形)的表面热流,取值为79.54 kW/m2。由于GSI为纯镜面反射(σ= 0)时气体分子与凹腔表面之间没有能量交换,故热流均为0。

图7 不同GSI模型对应的凹腔表面中心线热流分布Fig.7 Distributions of surface heat flux along centerlines of cavity surfaces for different GSI models

不同Maxwell适应系数对应的凹腔上游壁面(FW)热流分布与压力分布相似。除了σ=0.25之外,其他GSI模型对应的峰值热流均小于平板热流。GSI模型对FW的热流分布影响颇为明显：随着σ从1.00降低到0.25,FW的表面热流逐渐增大,镜面反射的峰值热流是漫反射的250余倍。因此,在飞行器气动设计中,如果一部分气体分子在其表面发生镜面反射时,需要特别留意表面缺陷或缝隙上游壁面的热载荷。

凹腔底面(CF)的热流分布与压力类似,随着σ从1.00降低到0.25,由于黏性剪切作用减弱导致外流被卷入的程度减弱,热流沿着CF的分布逐渐变得均匀。

不同Maxwell适应系数对应的凹腔下游壁面(AW)的热流分布同样呈现类似性：热流在AW底部较低,此后沿着AW向上直至凹腔后缘一直单调增大。与GSI模型对AW表面压力的影响不同,随着σ从1.00降低到0.25,AW表面热流逐渐降低。这是因为AW的表面热流主要来源于外流与该表面之间的黏性剪切,随着σ的降低,黏性剪切作用减弱,热流自然降低。

7 结 论

采用DSMC方法模拟稀薄流区高超声速凹腔绕流问题,考虑GSI模型的影响,探索Maxwell适应系数对凹腔流场特征和表面压力、热流的变化规律,得到结论如下：

1) 稀薄流条件(80 km)下,GSI为完全漫反射时,外部流动直接绕过凹腔,在凹腔前缘分离的剪切层再次附着在后缘,在凹腔内部形成一个充满腔体的单涡结构。

2) 随着GSI从完全漫反射向纯镜面反射变化,涡结构不断减小直至消失,凹腔底部逐渐出现所谓的“死水区”；凹腔内部的密度也逐渐减小,凹腔后缘的再附现象逐渐减弱甚至消失。

3) 随着GSI从完全漫反射向纯镜面反射变化,气体与凹腔表面之间的切向动量交换减弱,即黏性剪切作用减弱,外部气流被卷入凹腔的程度减弱,导致凹腔底面的压力和热流分布逐渐变得均匀。

4) 与GSI为完全漫反射相比,镜面反射导致凹腔上游侧面的峰值压力增大70余倍、下游侧面的峰值压力增大4倍多,近镜面反射(σ= 0.25)导致上游壁面的峰值热流增大250余倍,表明在飞行器设计中,如果一部分气体分子在其表面发生镜面反射时,应特别留意表面缺陷或缝隙上游壁面压力载荷、热载荷和下游壁面的压力载荷。