基于滑动L2优化准则的GPS坐标时间序列重构

周 侗，边家文*，丁开华，陈保周，伍浩琛

（1.中国地质大学 数学与物理学院，湖北 武汉 430074；2.中国地质大学 地理与信息工程学院，湖北 武汉 430074）

GPS监测技术已广泛应用于地壳形变、板块运动监测，地震、海啸预警，参考框架建立与维持等领域，因此精确地分析和估计GPS坐标时间序列具有重要意义。在精确分析和重构GPS坐标时间序列之前，需对GPS坐标时间序列的噪声类型进行分析，国内外学者对此进行了较为全面的研究，如MAO A L[1]等分析了全球23个GPS站点长达3 a的时间序列，结果表明噪声的最佳模型是“闪烁噪声+白噪声”；李昭[2]等分析了中国区域GPS坐标时间序列的噪声类型，结果表明测站最佳噪声模型组合为“闪烁噪声+白噪声”和“带通幂律噪声+白噪声”；在GPS坐标时间序列重构方面，WANG X M[3]和CHEN Q[4]等提出了利用奇异谱分析法（SSA）提取序列周期的方法，SSA方法可以较好地从含噪声的时间序列中提取信息，但在分离噪声时会吸收部分有色噪声；张双成[5]等利用经验模态分解（EMD）方法对GPS坐标时间序列进行了降噪和重构，EMD方法能合理地分离序列中的信号和噪声，有效削弱噪声对GPS坐标时间序列的影响，进一步提高GPS坐标时间序列的精度，但在噪声较大时，会出现模态混叠现象，导致重构效果较差；董伟[6]采用小波分解（WD）方法对GPS坐标时间序列进行了多分解、去噪和重构，WD方法可为任何调制信号建模时变多样的季节曲线，可在限制的频率之间模拟信号和噪声，从而确定分辨率，但不进行信号和噪声之间的分离；LIU N[7]和Didova O[8]等利用卡尔曼滤波方法（KF）对缺失的GPS坐标时间序列进行重构，KF方法的最大缺点是必须用到无限过去的数据。

近年来，Anna等提出利用滑动普通最小二乘法（MOLS）来重构信号。MOLS方法通过选取合适的窗口，滑动利用最小二乘得到每段的估计，最终得到整段GPS坐标时间序列的估计，速度较快，但由于忽略了噪声特性，导致精度较低，且会产生过拟合现象[9]。本文通过L2优化方法来防止过拟合，由于在整段时变周期的GPS坐标时间序列上采用L2优化方法会导致较大的误差，因此将信号分段，逐年滑动，在每段上使用L2优化方法，即滑动L2优化估计方法（ML2），并在每段采用交替迭代乘子法（ADMM）求解。ADMM算法具有分布式运算、并行处理的特点，且在迭代次数较少时能得到合理的精度[10]，使GPS坐标时间序列的重构精度更高。

1 模型与重构算法

1.1 GPS坐标时间序列的模型

GPS坐标时间序列的一般模型为：

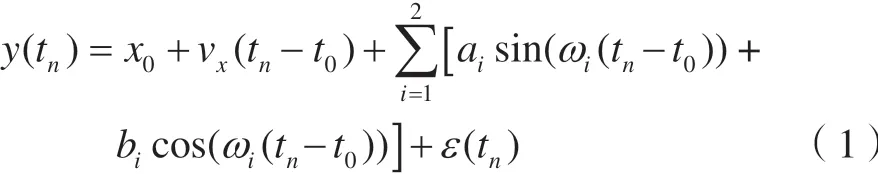
式中，n=1,2,…,N，N为信号长度；y(tn)为信号；x0和vx分别为初始位置和速度；ai和bi分别是角速度为ωi的周期信号的正弦和余弦项的常数；εt为噪声，本文采用“闪烁噪声+白噪声”的噪声模型；t0为参考时间；tn为时间。

在实际信号处理中周期信号的振幅ai和bi往往会随着时间发生变化[11]，因此本文利用的时变周期的GPS坐标时间序列模型为：

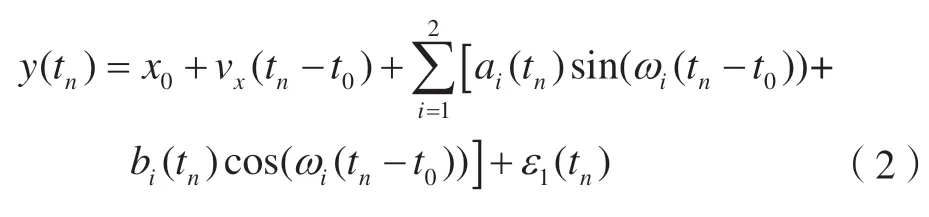
式中，ai(t)和bi(t)为时变振幅，假设它们由其均值和随机扰动组成，即ai(t)=ai+μi(t)，bi(t)=bi+vi(t)，μi(t)和vi(t)为随机扰动，因此需要估计时变振幅的均值。

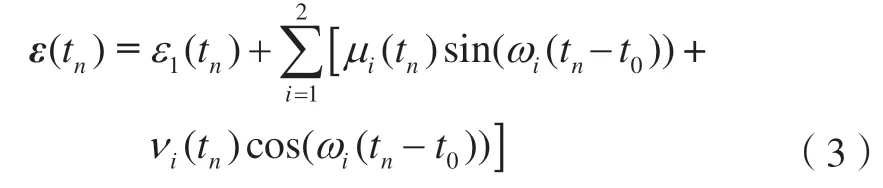
记：则式（2）可写为：

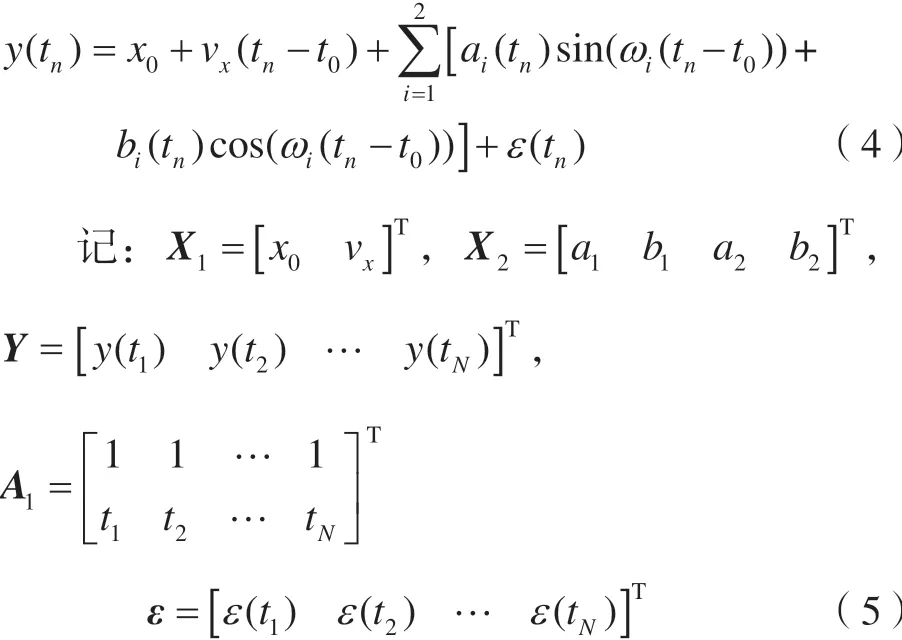
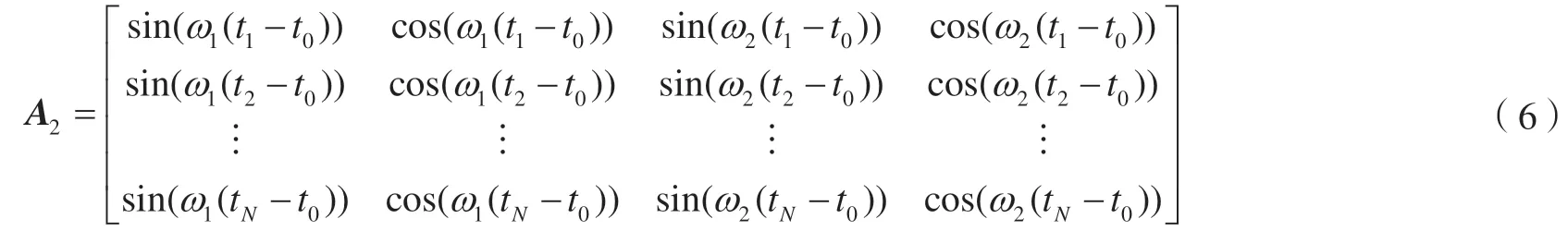
式（2）可转化为式（1），相应的矩阵表示形式为：

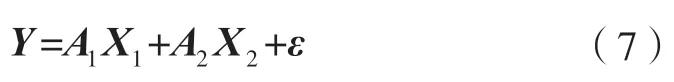
式中，A1X1为趋势项；A2X2为周期项；ε为噪声项。

1.2 基于L2优化准则的GPS坐标时间序列重构

1.2.1 优化模型

为了估计周期项和趋势项，建立的优化模型为：

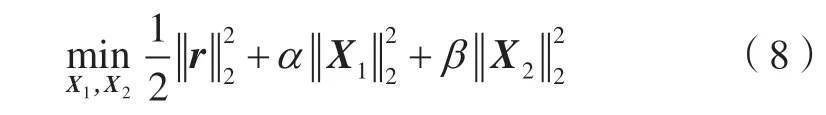
式中，r=Y-A1X1-A2X2；α和β为正则项的参数。本文采用L2范数约束参数X1和X2，防止参数X1和X2过拟合。

1.2.2 ADMM算法

ADMM算法既有乘子法的强收敛性质又有对偶上升法的分解性，因此该方法比较适合求解大规模的优化问题。目前，该方法已广泛应用于压缩感知、图像处理、机器学习等诸多领域。ADMM算法的优点是仅有一个参数ρ，且在一定条件下，其对任意参数均收敛。对于优化问题式（8），可使用梯度下降法求解，但该方法对步长的选择非常敏感，选择不合适的步长甚至会导致算法不收敛；而ADMM算法对步长具有较强的鲁棒性，在一定条件下，能保证对所有的步长都收敛[12]。因此，本文采用ADMM算法求解优化问题式（8）。

构造优化问题式（8）的增广拉格朗日函数，则有：

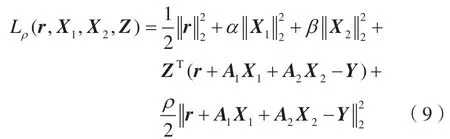
式中，Z为对偶变量并具有适当的缩放尺寸；ρ为惩罚参数[13]。

按照顺序更新变量r、X1和X2，再更新对偶变量Z，即

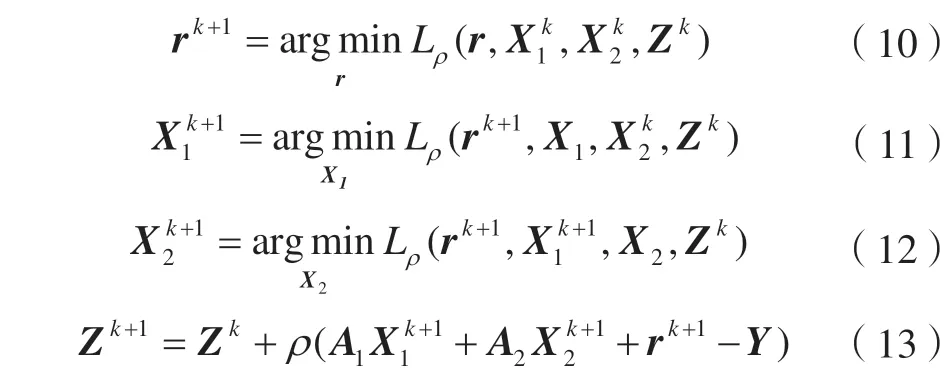
对式（10）的优化目标函数进行简化，可得：

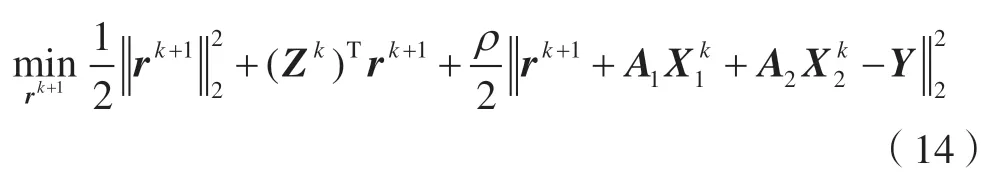
对rk+1求导，令结果为0，则有：

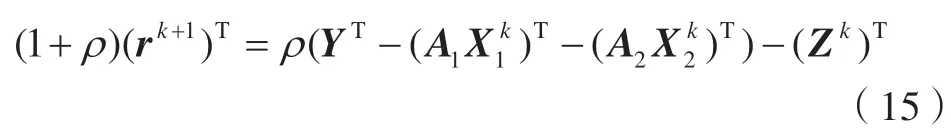
可得rk+1的迭代公式为：

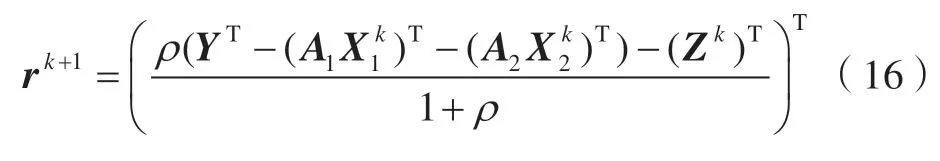
对式（11）的优化目标函数进行简化，则有：

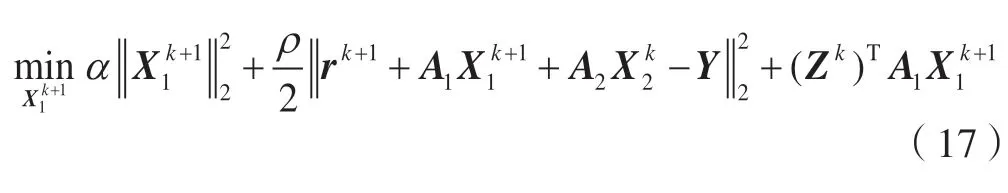
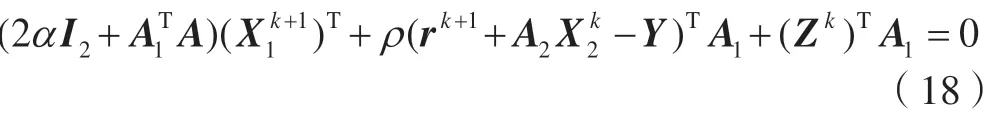
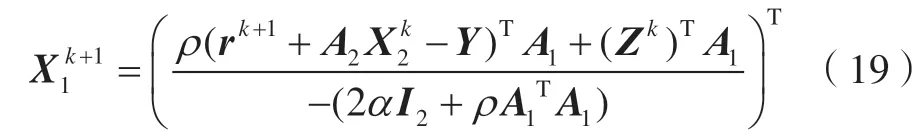
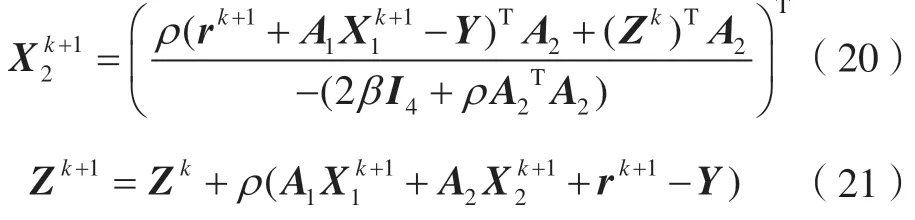
式中，I2和I4分别为2阶单位矩阵和4阶单位矩阵。

ADMM算法的收敛性由其残差来刻画，其停止准则为：

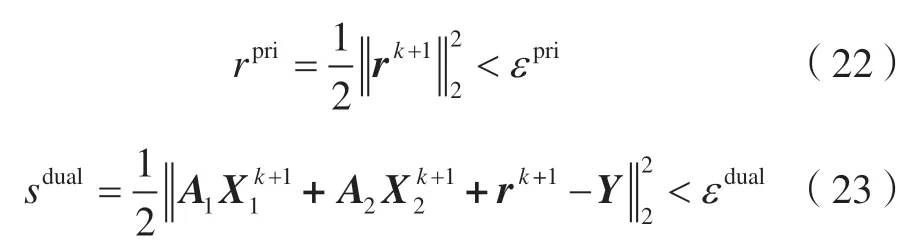
式中，rpri为原始误差；sdual为对偶误差；εpri和εdual为给定的阈值。

1.2.3 算法评价指标和计算公式

本文采用4个评价指标全面衡量重构信号的效果，通过Misfit衡量重构信号和真实信号的误差，噪声谱指数和噪声振幅衡量残差和真实噪声的接近程度，速度不确定度衡量残差对速度估计的影响。

1）Misfit为真实信号和重构信号的标准差。2）噪声谱指数（κ）。功率谱的计算公式为[14]：

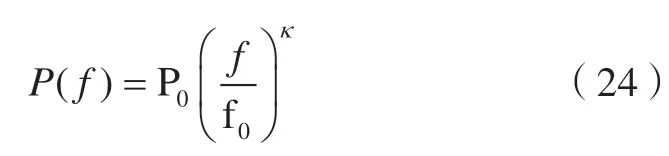
两边取对数，则有：

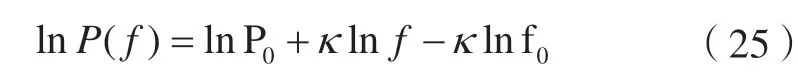
式中，P(f)为功率谱密度（本文采用经典周期图法计算）；f为频率；P0和f0为常量。本文采用最小二乘法估计噪声谱指数。

3）噪声振幅（σ）。本文采用的噪声模型为：

式中，α为白噪声；e为白噪声的振幅；βκ为谱指数为κ的有色噪声（κ=-1为闪烁噪声）；σ为谱指数为κ的有色噪声的振幅[15]。

ε的协方差矩阵C的计算公式为[16]：

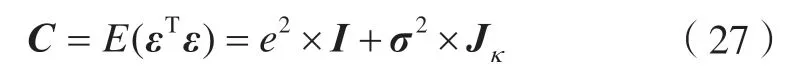
式中，I为单位矩阵；Jκ为谱指数为κ的噪声的单位协方差矩阵。

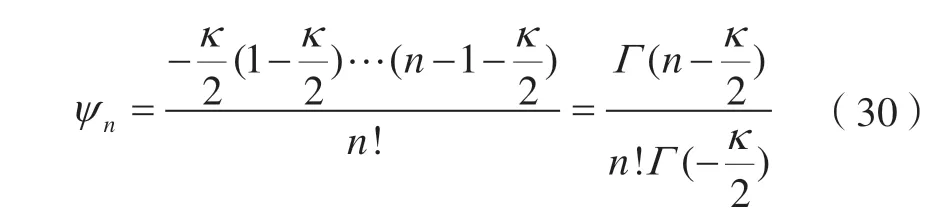
4）速度不确定度（Uv）[17-19]。

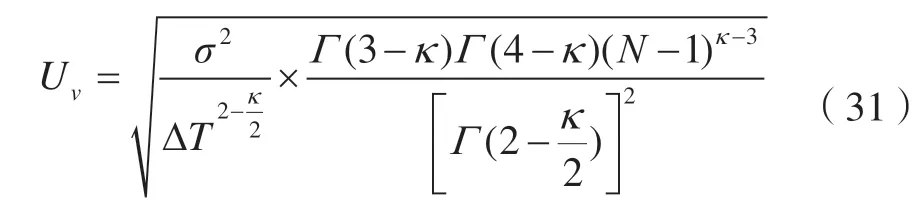
式中，ΔT为时间间隔；Γ为Gamma函数。

1.2.4 算法流程

通过上述分析，基于L2优化准则的GPS坐标时间序列重构方法的具体步骤为：①根据式（2）产生时变周期的GPS坐标时间序列；②根据式（3）建立矩阵A1和A2；③根据信号的长度N，选取合适的分段长度W，并逐年滑动得到M段信号（M=([N/365]-W)+2）；④针对每段信号建立式（8）的优化模型，再按照迭代步骤估计参数X1，X2；⑤初始化α、β、ρ、r、X1、X2、Z、εpri、εdual、rpri、sdual；⑥利用式（16）得到r第k次的更新rik；⑦利用式（19）得到X1的第k次更新Xk1,i；⑧利用式（20）得到X2的第k次更新Xk2,i；⑨利用式（21）得到Z的第k次更新Zik；⑩根据式（22）和式（23）分别计算rpri和sdual；⑪若rpri和sdual满足式（22）和式（23）则终止循环，否则继续重复步骤⑥～⑨；⑫重复步骤④～⑪，直到得到每段时间序列的估计；⑬依据X1和X2逐年恢复信号（重复的年份取平均），并得到残差；⑭根据式（25），利用最小二乘法得到残差的谱指数估计；⑮根据式（26）～（30），利用最大似然法得到残差的振幅估计；⑯计算重构信号的Misfit，并根据式（31）计算速度不确定度。

2 模拟实验

本文采用两组模拟数据来检验本文提出的算法性能，并与MOLS、SSA和WD方法进行对比。实验中MOLS每段时间长度为1 100 d，滑动间隔为1 a，SSA的窗口大小为4 a（窗口大小为1 460 d），WD方法采用的是Meyer小波。本文利用Misfit、噪声谱指数、噪声振幅和速度不确定度来衡量重构信号的精度。

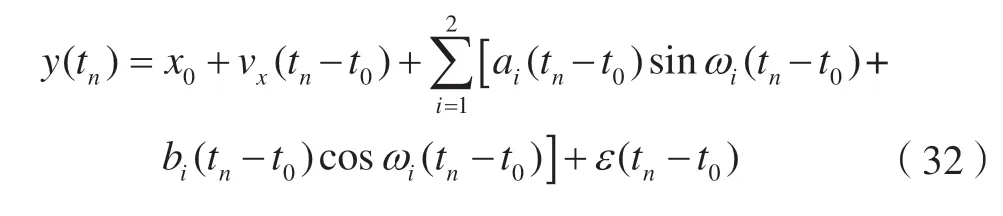
模拟数据的参数为：t0=0，x0=10 mm，vx=5 mm/a，a1,b1～N(3,1)，a2,b2～N(2,0.5)，ω1=2π/365，ω2=4π/365。为了验证算法在有色噪声干扰情形下的有效性，本文模拟实验的噪声取为闪烁噪声。闪烁噪声较小时，闪烁噪声振幅取为1 mm/a-1/4；闪烁噪声较大时，闪烁噪声振幅取为10 mm/a-1/4。实验结果如表1、2所示。

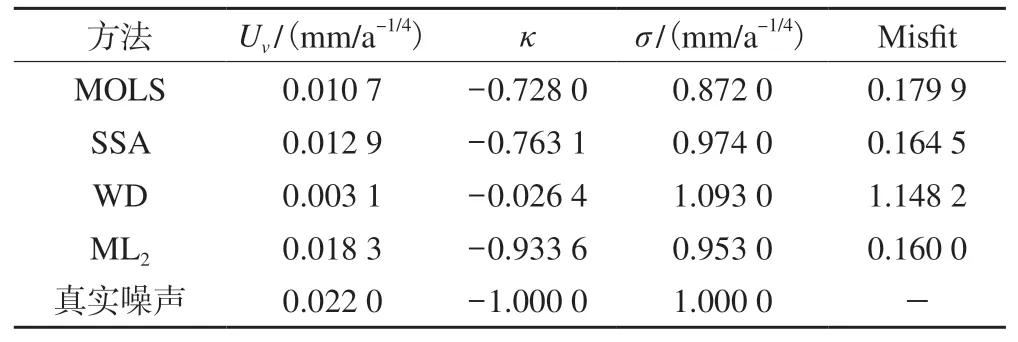
表1 噪声振幅为1 mm/a-1/4的实验结果

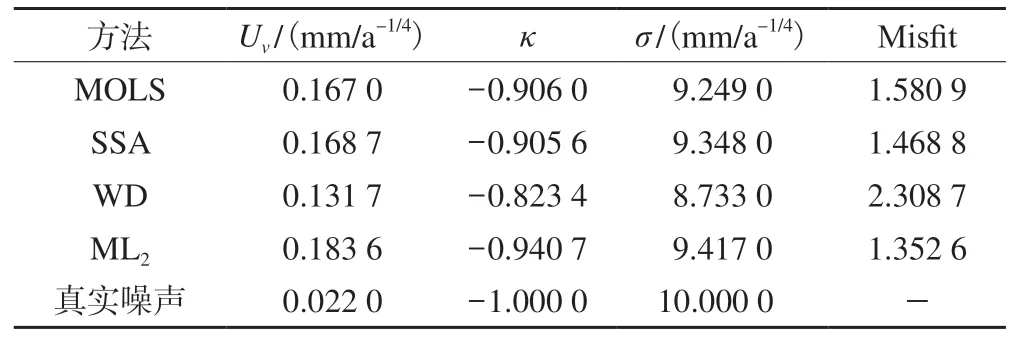
表2 噪声振幅为10 mm/a-1/4的实验结果

4种方法重构的GPS坐标时间序列对比如图1所示，可以看出，ML2比其他3种方法具有更好的重构效果，且MOLS方法过拟合导致重构GPS坐标时间序列吸收了部分噪声，而ML2方法则避免了这一点，因此效果更好。由表1、2可知，ML2方法拥有最小的Misfit，且噪声谱指数和噪声振幅与真实的最接近；SSA和MOLS方法的Misfit较大，且在噪声较小时SSA和MOLS方法会吸收闪烁噪声，导致噪声谱指数的估计较差；WD方法会吸收大量的噪声导致误差较大，尤其是在噪声较小时，WD方法与其他方法相比误差更大，重构效果最差；MOLS方法在重构GPS坐标时间序列时会吸收部分噪声，从而导致过拟合，该现象在噪声较小时尤为明显，ML2方法则有效避免了这一缺点。4种方法的频谱图如图2所示，period为真实周期，可以看出，这4种方法均能提取周期，MOLS、SSA和ML2方法均有较好表现，而WD方法则吸收了较多噪声，效果较差，尤其在噪声振幅较小时，WD方法失真。图2也证实了ML2方法能减少过拟合，从而有更好的重构效果。

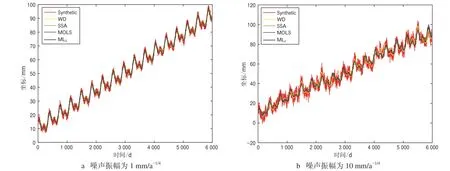
图1 4种方法的GPS坐标时间序列重构比较

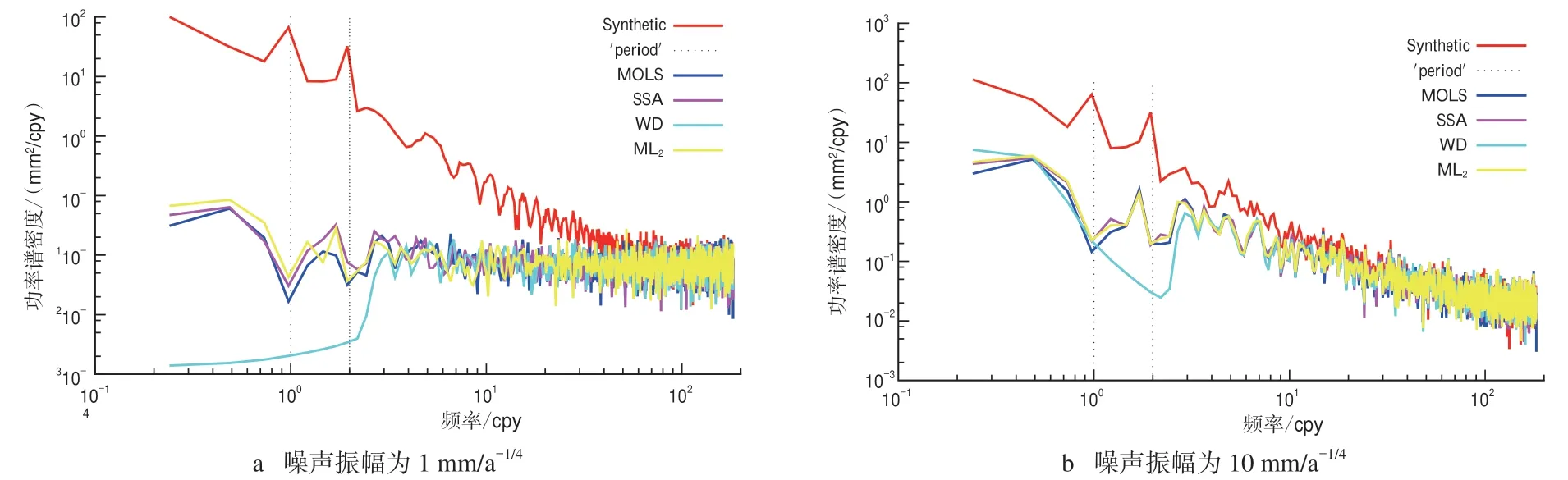
图2 4种方法的残差功率谱比较

3 真实数据分析

本文选取的是北京房山站1999-2017年的数据，实际GPS坐标时间序列缺失部分数据，且含有野值（数据观测错误），因此需对数据进行预处理。首先利用3σ准则（拉依达准则）去除野值，然后利用线性插值对缺失的部分进行补全，最后进行GPS坐标时间序列的重构。为了说明ML2方法的有效性，本文通过计算相关系数来比较4种方法之间的相似性。

实验结果如表3所示，房山站U方向4种方法的相关性如表4所示，可以看出，ML2方法介于几种方法之间，有着与其他方法相同的表现；ML2方法与MOLS方法和SSA方法的相关性较高与WD方法相关性较低；与MOLS方法相比，ML2方法减少了过拟合，从而具有更好的效果。4种方法U方向的功率谱如图3所示，可以看出，ML2方法的重构效果优于MOLS方法，表明ML2方法能通过减少过拟合来提高GPS坐标时间序列的重构精度。

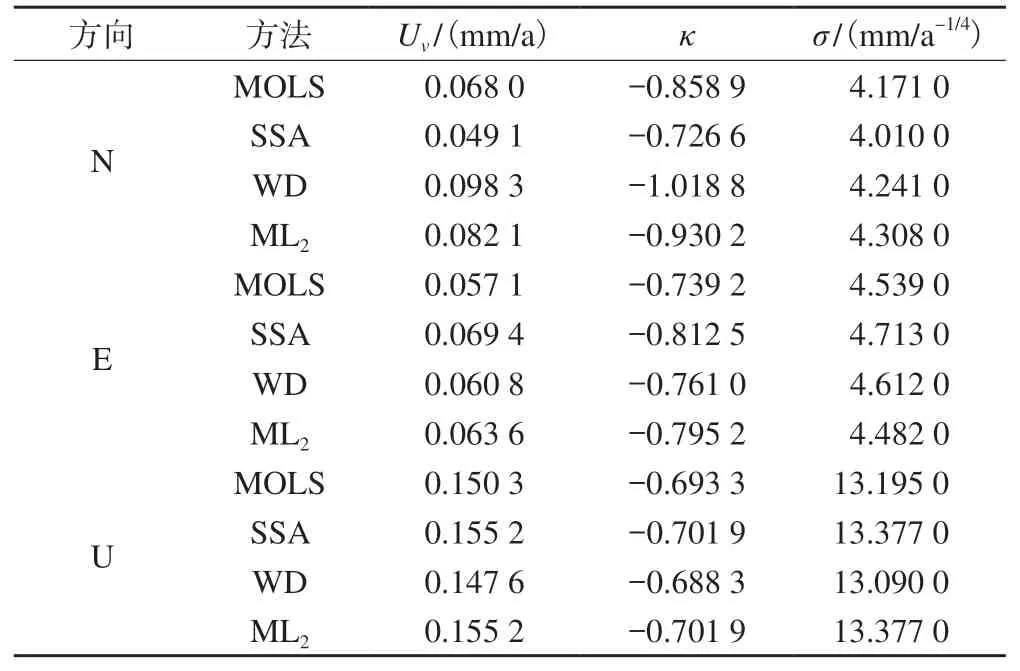
表3 房山站3个方向的实验结果

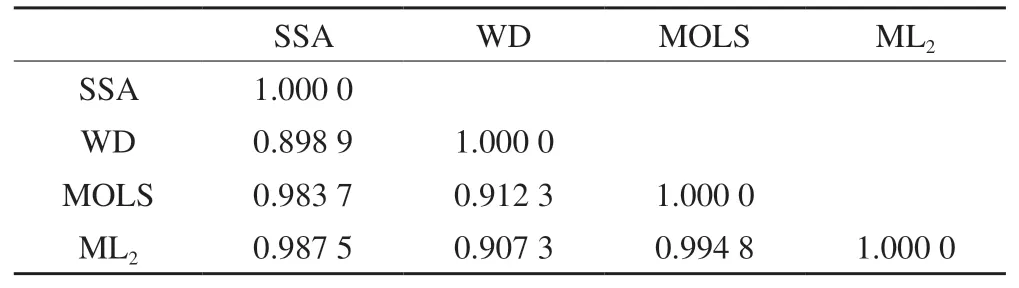
表4 房山站U方向4种方法的相关性

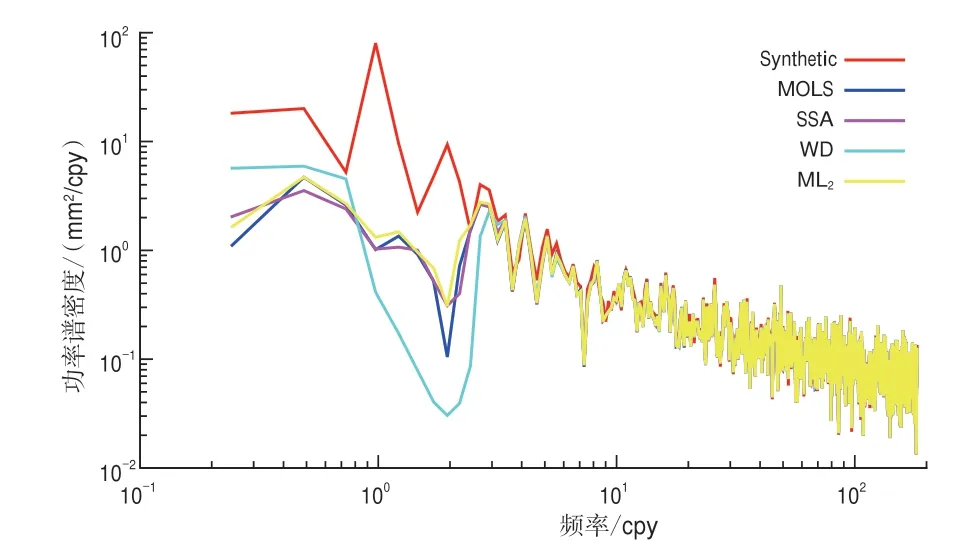
图3 房山站U方向4种方法的功率谱

4 结 语

本文研究了坐标时间序列的重构，将时变的GPS坐标时间序列模型转化为一般的GPS坐标时间序列模型。为了重构GPS坐标时间序列，本文采用ML2方法建立了优化模型，以防止过拟合，在噪声较大时能获得更好的重构效果；利用ADMM算法求解优化模型，并采用滑动的方法重构GPS坐标时间序列。通过模拟数据和真实数据的实验得到以下结论：

1）在模拟数据实验中，ML2方法能重构GPS坐标时间序列，与MOLS、SSA和WD方法相比具有最小的Misfit。从模拟实验的结果来看，ML2方法比MOLS方法的效果更好，避免了过拟合问题，使得重构的精度更高；从真实数据实验的结果来看，ML2方法的效果介于几种方法之间，证明了ML2的有效性，且与MOLS方法相比具有更好的重构效果，这也表明了ML2方法能避免过拟合问题，从而使重构精度更高。2）SSA和WD方法在信号太弱的情形下难以准确分离信号和噪声，而ML2方法则在该情形下能够得到较好的重构效果，这也体现了ML2方法相较于其他重构方法的优越性。