高强方钢管—混凝土—圆钢管组合短柱轴压性能
李晓丽, 陈 莉
( 东北石油大学 土木建筑工程学院,黑龙江 大庆 163318 )
0 引言
随中国建筑领域不断发展,新型建筑物逐渐向高耸大跨智能舒适的方向拓展,随建筑物高度及使用功能增加,对构件的承载性能及适用条件提出更高要求,使普通钢管混凝土的适应能力面临新挑战。若继续采用单层钢管约束的混凝土柱,只能不断提高构件截面面积和内部混凝土强度满足建筑物的承载要求,容易导致构件自重过大或因高强混凝土使构件出现延性差和脆性高等不利因素。高强方钢管—混凝土—圆钢管(HSCS)组合短柱主要构造形式为内圆钢管和外高强方钢管同心摆放,其间填充环混凝土。外钢管采用高性能约束材料可有效提高组合柱的轴压性能[1],高强钢管能为混凝土提供必要的约束效应和一部分轴压增益[2]。环混凝土受外钢管的约束及内钢管的横向支撑,处于三向应力状态,加上环混凝土的支撑作用,可有效延缓或避免钢管在受力过程中的局部屈曲或整体屈曲破坏。中空的内钢管也具有极大的构造优势,对环混凝土提供必要的支撑作用,避免受力过程中环混凝土因挤压变形而局部脱落。中空构造能有效降低组合柱的自重,减轻结构物对基础施加的自重压力,还可以满足建筑管线穿插及必要的结构健康监测设备的摆放,符合现代智能建筑理念的需求。
钢管混凝土柱在高层建筑中得到广泛应用[3-4],有效提高建筑物的承载性能。CHNEIDER S P[5]开展14根钢管混凝土短柱的轴压性能试验研究,表明钢管的存在大幅改善组合构件的刚度与延性。韩林海[6]对单钢管混凝土柱的轴心、偏心受压及抗火等性能进行阐述,建立并完善钢管约束混凝土理论。蔡绍怀等[7]开展多钢管(数量≤2)混凝土组合柱轴压性能研究,发现实际工程中宜采用同心双钢管,因第三层及更多层钢管对组合柱的轴压性能增益并不显著,而且增加施工难度。EKMEKYAPAR T等[8]开展实心复式钢管混凝土组合柱轴压试验,获得不同参数下试件的轴向荷载—位移曲线及其破坏形态,证明该类组合柱在强度、刚度和延性性能方面的能力,但构件自重过大。TAO Z等[9]根据约束混凝土理论,获得中空钢管混凝土组合柱的应力—应变全过程曲线,并证明其具有精确的预测精度。丛术平等[10]开展6根缩尺方中空钢管混凝土短柱轴压性能试验,获得试件的轴向荷载—应变曲线,并分析不同参数对组合柱轴压性能的影响。UENAKA K等[11]开展中空双钢管混凝土柱试验,证明该类短柱的破坏主要由外层钢管局部屈曲或撕裂造成的。YANG Y F等[12]开展14根圆形空心双钢管混凝土短柱和15个方形空心双钢管混凝土短柱的局部受压试验,发现两种截面的空心双钢管混凝土短柱在局部压力作用下表现优异的变形能力。
目前,关于中空双钢管混凝土试件轴压性能研究的成果较多,但多数是基于缩尺试件,关于各个参数对该类足尺试件力学性能的影响分析较少,涉及外层高强钢管的介绍更少。鉴于该类试件具有优异的力学性能,有必要开展高强方钢管—混凝土—圆钢管(HSCS)组合短柱轴压性能研究。
1 试件设计
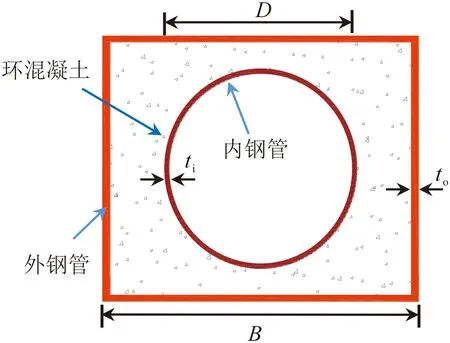
图1 HSCS组合短柱示意
为获得足尺的HSCS组合短柱的轴压性能,以环混凝土轴心抗压强度(fck)、外高强方钢管的抗拉强度(fyo)、壁厚(to)和宽度(B)、内圆钢管的抗拉强度(fyi)、壁厚(ti)和直径(D),以及试件的长细比(λ)和空心率(T)、约束效应因数(ξ)等为控制参数,共设计27根足尺的HSCS组合短柱试件,试件设计参数见图1和表1。
λ=4l/B,
(1)
T=Asic/Asoc,
(2)
式中:l为试件高度;B为方形高强钢管的边长;Asic和Asoc分别为内圆钢管和外方钢管包围的面积。文中设计的试件长细比小于8,属于短柱范畴。
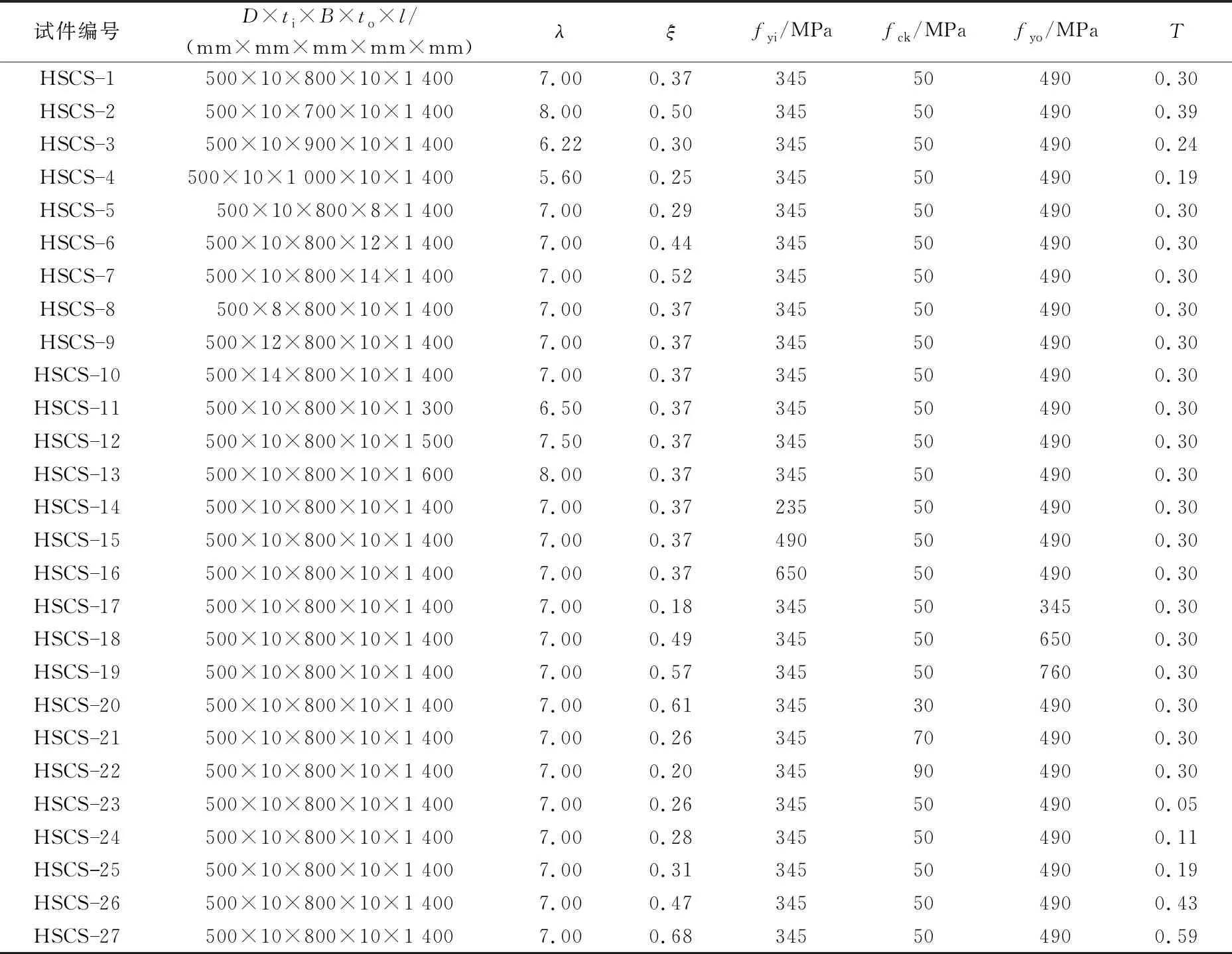
表1 HSCS组合短柱设计参数
2 有限元模型建立
2.1 建模过程
采用ABAQUS有限元分析软件对试件进行建模分析时,钢管和混凝土采用三维实体可拉伸单元。钢材三向属性差别不大,采用考虑塑性硬化的双线性本构模型[13](见图2(a))。仿真分析采用约束混凝土本构模型[6]无约束混凝土的本构模型(见图2(b))[14],具体变量意义和计算方法见文献[6,13-14]。
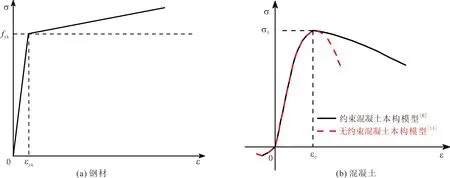
图2 材料本构模型
模拟试验的加载方式,在有限元模型两端设置两个参考点(RP1和RP2)并分别与构件上下两截面耦合,轴压荷载可通过参考点均匀施加于整个截面。由于组合柱内各材料和部件间具有相互作用,在建立有限元模型过程中,将各部件界面间的接触方式定义为面面接触。钢管与混凝土的接触模式由切向行为下的摩擦接触及法向行为下的硬接触组成,并允许接触后分离。通过设置全局种子布种,网格形状以六面体为主。
2.2 验证分析
为验证HSCS组合短柱建模过程的合理性,选取文献[10]中6个类似试验进行验证,参数见表2。
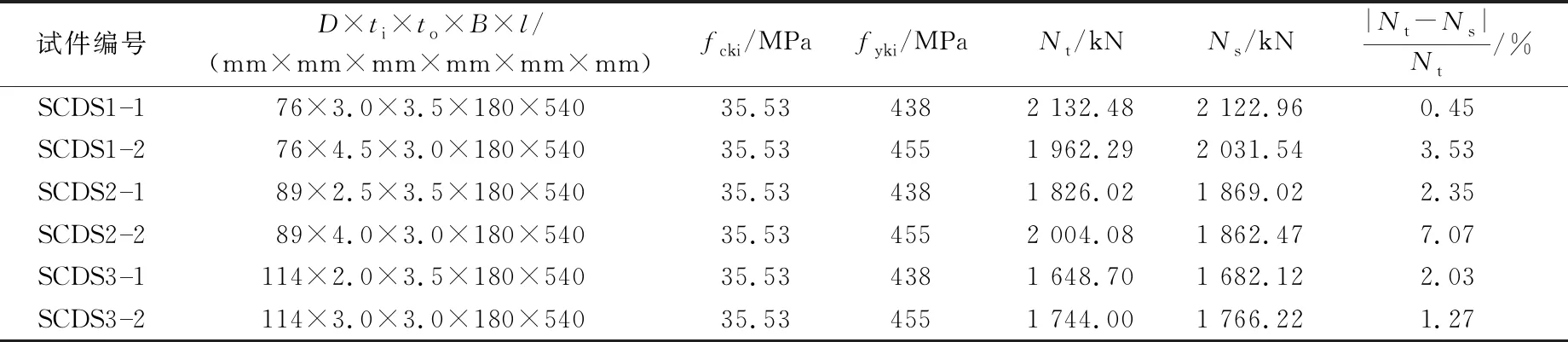
表2 6个类似试验的试件参数
2.2.1 网格适应性
为确定合理的网格尺寸,首先执行一个较大的网格进行初始分析,再利用1/2的网格重新分析并比较二者的结果。如果二者结果的差别较小(小于1%),则网格尺寸满足要求;否则,应继续细化网格[15]。对试件SCDS1-1进行4种网格尺寸划分,其中环混凝土采用考虑约束效应下的本构模型,网格尺寸分别选取为l/15、l/30、l/60和l/120。获得不同网格划分方法下试件SCDS1-1的轴向荷载(N)—轴向应变(ε)的关系曲线和轴压承载力(Ns)—网格尺寸曲线(见图3)。
对SCDS1-1试件采用2.1建模方法进行模拟分析(见图3(a)),网格尺寸分别选取l/15、l/30、l/60和l/120时,其N—ε曲线的变化幅度基本类似,出现明显的峰值点及下降段,经过峰值点后,曲线逐渐趋于平缓,轴压承载力随网格尺寸的细化而逐渐递增;由图3(b)可知,当网格尺寸由l/15增到l/30、l/60和l/120时,试件仿真分析下的轴压承载力(Ns)由2 080.50 kN增到2 122.96、2 143.77、2 165.64 kN,增加幅度分别为2.00%、0.97%、1.01%,网格尺寸选取l/30满足要求,各部件网格划分方法见图4。

图3 网格尺寸对SCDS1-1试件的影响
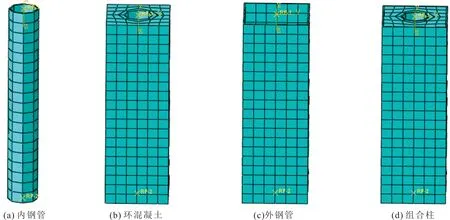
图4 组合柱网格划分方法
2.2.2 实验
基于2.1建模方法,对表2的6个试件开展验证分析,环混凝土的本构模型分别选取约束及无约束混凝土本构模型[14],考虑混凝土的塑性损伤演化特性,获得N—ε关系曲线(见图5)。由图5可知,6个类似试件环混凝土采用不同约束混凝土本构模型,在弹性阶段获得吻合程度较高的仿真结果,仅存微小差异,可能是由试验中混凝土的离散特性所致;在塑性阶段,采用约束混凝土本构模型的吻合程度明显高于无约束的。约束混凝土本构模型模拟的轴压承载力(Ns)与试验的轴压承载力(Nt)对比见图6,二者轴压承载力之间的最大误差为7.07%,小于15%,满足工程要求。
3 仿真结果分析
3.1 不同参数对足尺HSCS组合短柱轴压承载力的影响
3.1.1 外高强方钢管宽度
不同外高强方钢管宽度(B)的HSCS组合短柱试件N—Δ对比曲线见图7。当B由700 mm增加到800、900、1 000 mm时,试件的轴压承载力由34 643.00 kN增加到45 134.00、54 992.50和67 251.60 kN,分别提高30.28%、21.84%、22.29%,试件的极限位移由27.23 mm降低到26.90、26.16和25.37 mm,分别降低1.21%、2.75%、3.01%,弹性阶段的刚度逐渐增大,塑性阶段的持荷能力逐渐降低。基于文中参数范围,随B的增大,HSCS组合短柱试件的轴压承载力增幅较大,极限位移降幅较小,所以HSCS组合短柱试件的轴压性能随B的增大逐渐增强。可见,长细比(λ<8)在短柱范围内时,试件高度不变,改变宽度对试件轴压性能影响较大。

图5 6个类似试件试验与模拟结果对比
3.1.2 外高强方钢管厚度
不同外高强方钢管厚度(to)的HSCS组合短柱试件N—Δ对比曲线见图8。当to由8 mm增加到10、12、14 mm时,试件的轴压承载力由41 940.30 kN增到45 134.00、48 372.00、51 625.90 kN,分别提高7.61%、7.17%、6.73%,试件的极限位移由26.07 mm增加到26.90、27.26、27.51 mm,分别增加3.19%、1.35%、0.89%。弹性阶段的刚度逐渐增大,但增幅较小,塑性阶段的持荷能力不变。基于文中参数范围,试件表现较强的持荷能力,随to的增大,HSCS组合短柱试件的轴压承载力逐渐增大,极限位移逐渐减小且降幅较小,降幅跨度也在逐渐缩小,故HSCS组合短柱试件的轴压性能随to的增大逐渐增强。
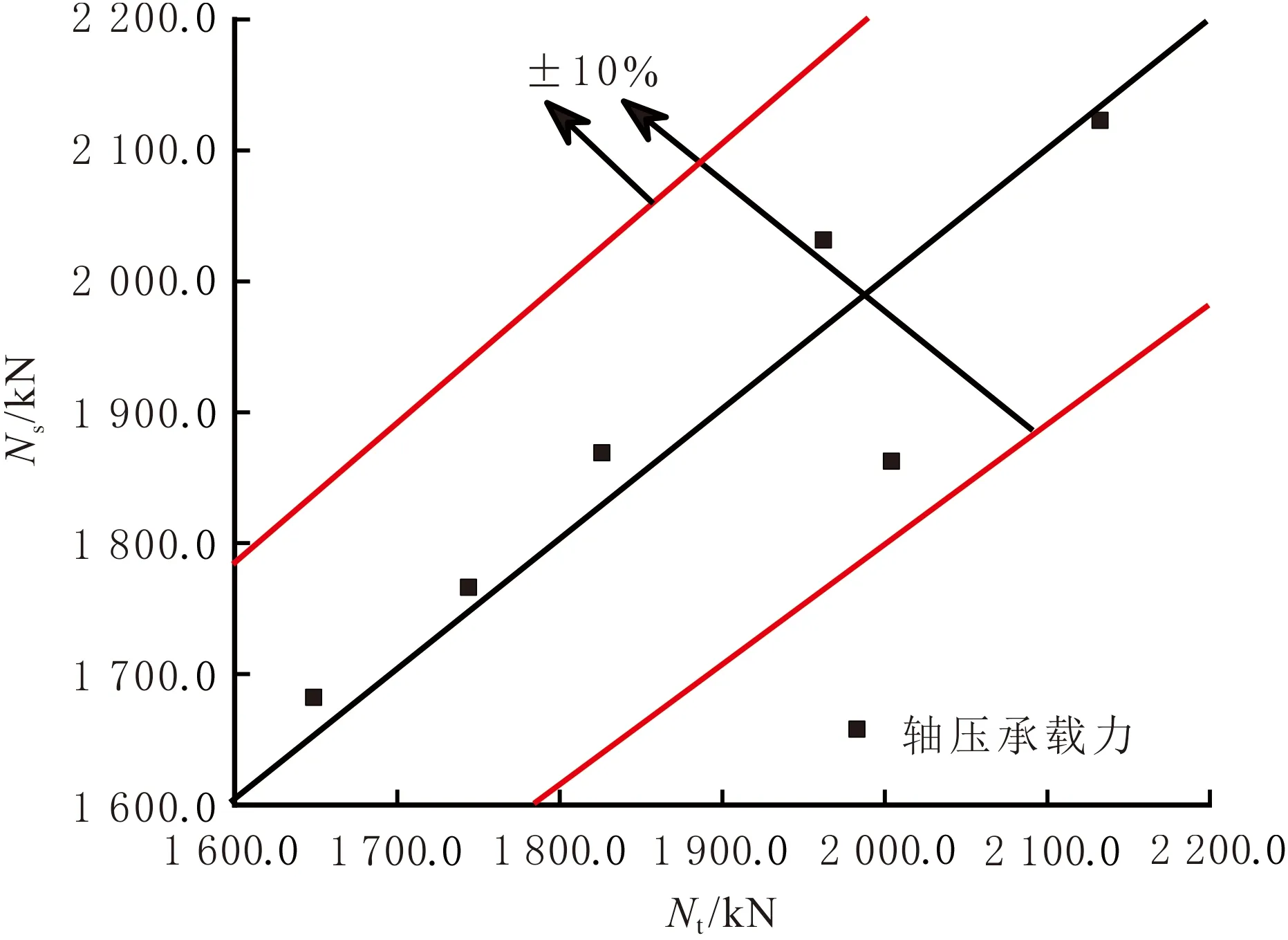
图6 Ns和Nt对比
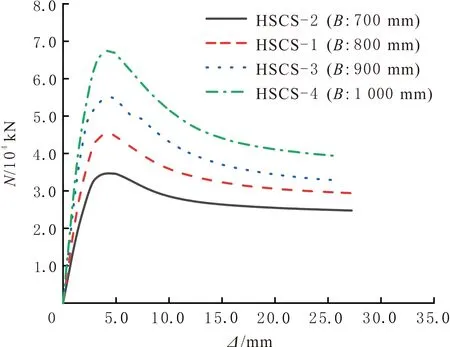
图7 不同B的HSCS组合短柱试件N—Δ曲线

图8 不同to的HSCS组合短柱试件N—Δ曲线
3.1.3 内圆钢管厚度
不同内圆钢管厚度(ti)的HSCS组合短柱试件N—Δ对比曲线见图9。由图9可知,当ti由8 mm增加到10、12、14 mm时,试件的轴压承载力由44 222.90 kN增加到45 134.00、46 222.10、46 977.00 kN,分别提高2.06%、2.41%、1.63%。试件的极限位移没有变化。基于文中参数范围,HSCS组合短柱试件表现较强的持荷能力,随ti的增大,HSCS组合短柱试件的轴压承载力逐渐增加,但增幅较小,极限位移保持不变,故HSCS组合短柱试件的轴压性随ti的增大有微弱增强。
3.1.4 试件高度
不同试件高度(l)的HSCS组合短柱试件N—Δ对比曲线见图10。当l由1 300 mm增加到1 400、1 500、1 600 mm时,试件的轴压承载力由45 549.40 kN降低到45 134.00、44 603.00、44 578.90 kN,分别降低0.91%、1.18%、0.05%,试件的极限位移由26.80 mm增加到26.90、27.12、27.36 mm,分别增加0.39%、0.83%和0.88%。弹性阶段的刚度逐渐减小,但减幅较小。基于文中参数范围,试件表现较强的持荷能力,随l的增大,HSCS组合短柱试件的轴压承载力逐渐减小,极限位移逐渐增大,变化幅度较小,可见,长细比(λ<8)处于短柱范围内时,HSCS组合短柱试件宽度不变,改变试件的高度对其轴压性能的影响较小。
3.1.5 内圆钢管强度
不同内圆钢管强度(fyi)的HSCS组合短柱试件N—Δ对比曲线见图11。由图11可知,当fyi由235 MPa增加到345、490、650 MPa时,试件的轴压承载力由43 169.20 kN增加到45 134.00、47 420.30、49 910.20 kN,分别提高4.55%、5.07%、5.25%,试件的极限位移由27.11 mm降低到26.90、26.73、26.03 mm,分别降低0.77%、0.64%、2.61%。基于文中参数范围,试件表现较强的持荷能力,随fyi的增大,HSCS组合短柱试件的轴压承载力逐渐增大,内圆钢管由不同钢材转换为高强钢材时,试件的极限位移逐渐减小,且降幅跨度逐渐增大。可见,高强钢材作为内钢管可有效提高试件的轴压承载力,但会牺牲一小部分极限位移,因此,HSCS组合短柱试件的轴压性能随fyi的增大逐渐增强,fyi应保证在合理范围内。
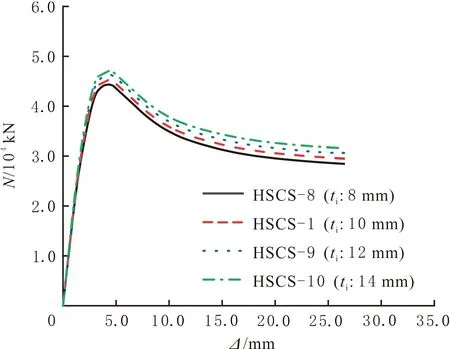
图9 不同ti的HSCS组合短柱试件N—Δ曲线
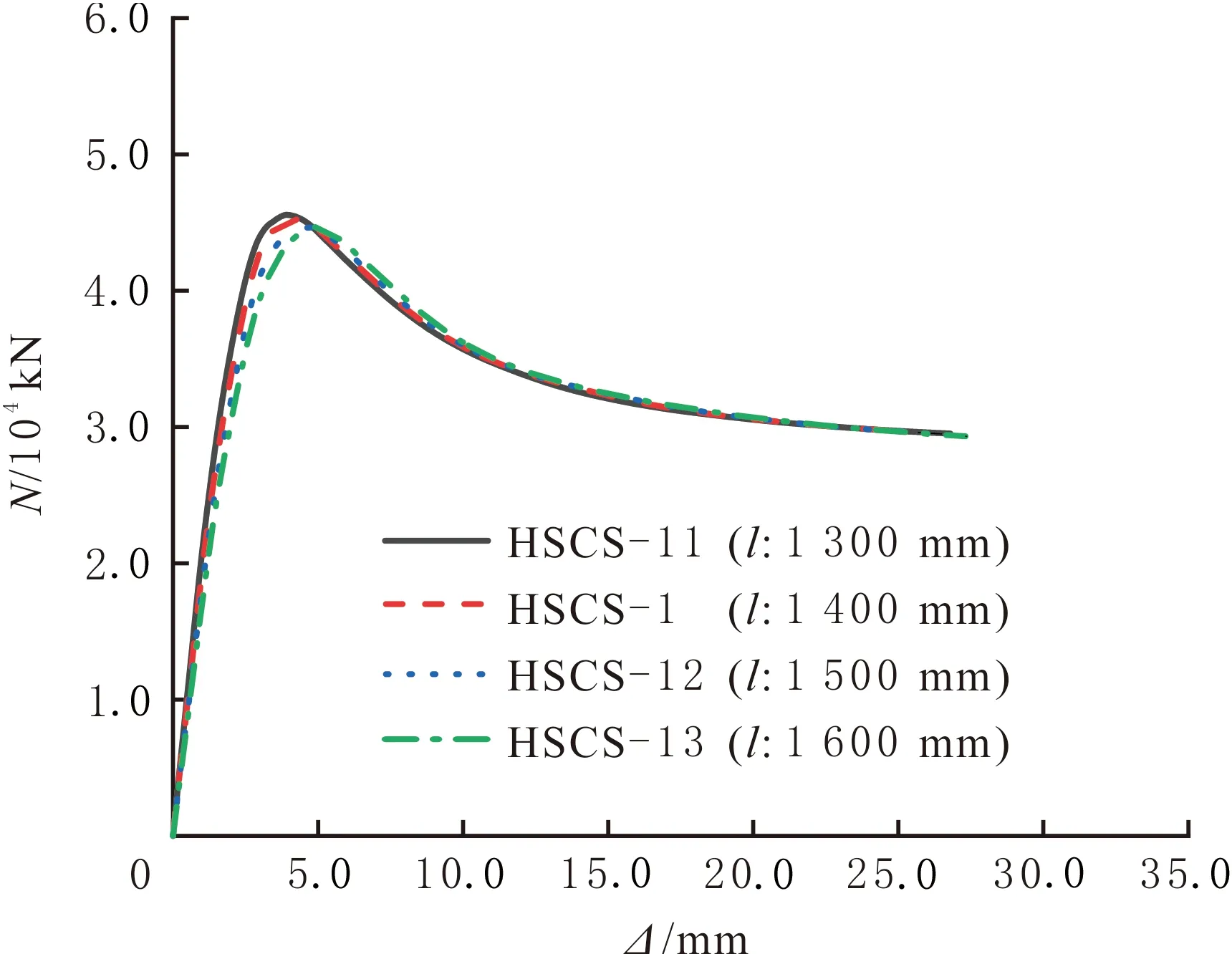
图10 不同l的HSCS组合短柱试件N—Δ曲线
3.1.6 外高强方钢管强度
不同外高强方钢管强度(fyo)的HSCS组合短柱试件N—Δ对比曲线见图12,为方便对比,试件HSCS-17外方钢管采用普通强度。由图12可知,当fyo由345 MPa增加到490、650、760 MPa时,试件的轴压承载力由40 194.70 kN增加到45 134.00、50 054.50、53 436.50 kN,分别提高12.29%、10.91%、10.75%,试件的极限位移由27.20 mm降低到26.90、26.24、25.16 mm,分别降低1.10%、2.44%、4.44%。基于文中参数范围,试件表现较强的持荷能力,随fyo的增大,HSCS组合短柱试件的轴压承载力逐渐增大,外方钢管由不同钢材转换为高强钢材时,试件的极限位移逐渐减小,且其降幅跨度也在逐渐增大。可见,高强钢材作为外方钢管可显著提高试件的轴压承载力,但会牺牲一小部分极限位移,因此,HSCS组合短柱试件的轴压性能随fyo的增大逐渐增强,fyi应保证在合理范围内。这与文献[1]得出的结论一致,且对比图11和图12可知,外层钢管对HSCS组合短柱轴压性能的提升更有利,提升幅度约为同等强度增幅下内层钢管的2倍。
3.1.7 环混凝土强度
不同环混凝土强度(fck)的HSCS组合短柱试件N—Δ对比曲线见图13。由图13可知,当fck由30 MPa增加到50、70、90 MPa时,试件的轴压承载力由36 480.80 kN增加到45 134.00、52 737.20、59 452.60 kN,分别提高23.72%、16.85%、12.72%,试件的极限位移保持不变,弹性阶段的刚度逐渐增大,塑性阶段的持荷能力逐渐降低。基于文中参数范围,试件表现较强的持荷能力,随fck的增大,HSCS组合短柱试件的轴压承载力逐渐增大,而环混凝土由普通强度转换为高强混凝土时,轴压承载力的增幅减弱,试件的极限位移不变。可见,fck的提高可有效提高试件的轴压承载力,但其增加幅度逐渐减小,因此HSCS组合短柱试件的轴压性能随fck的增大逐渐增强,fck应保证在合理范围内,以实现建筑材料利用效率的最大化。
3.1.8 截面空心率
不同截面空心率(T)的HSCS组合短柱试件N—Δ对比曲线见图14。由图14可知,当T由0.05增加到0.11、0.19、0.30、0.43、0.59时,试件的轴压承载力由51 779.60 kN降低到50 582.10、47 789.90、45 134.00、41 371.70、59 452.60 kN,分别降低2.31%、5.52%、5.56%、8.34%、12.23%,试件的极限位移由21.29增加到24.60、25.77、26.90、27.47、27.96 mm,分别提高15.55%、4.77%、4.39%、2.11%、1.78%,弹性阶段的刚度逐渐增大,塑性阶段的持荷能力逐渐降低。基于文中参数范围,试件表现较强的持荷能力,随T的增大,HSCS组合短柱试件的轴压承载力逐渐降低,其降低幅度随T的增大而逐渐增大,试件的极限位移增大,其增大幅度随T的增大而逐渐减小。可见,T在适当范围内取值对保持组合柱的轴压性能较为重要,为保证HSCS组合短柱的轴压性能,建议T的取值为0.1~0.3。
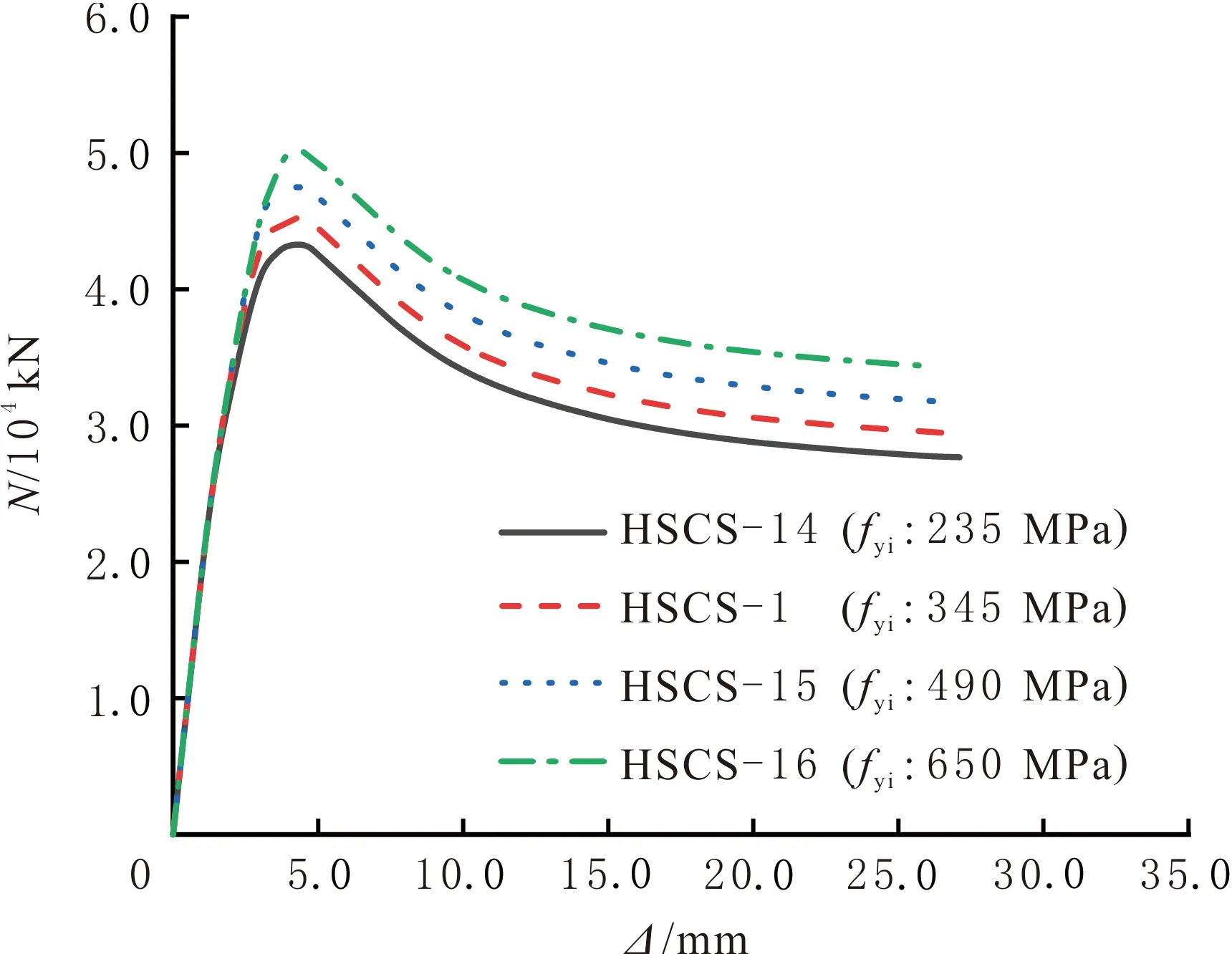
图11 不同fyi的HSCS组合短柱试件N—Δ曲线
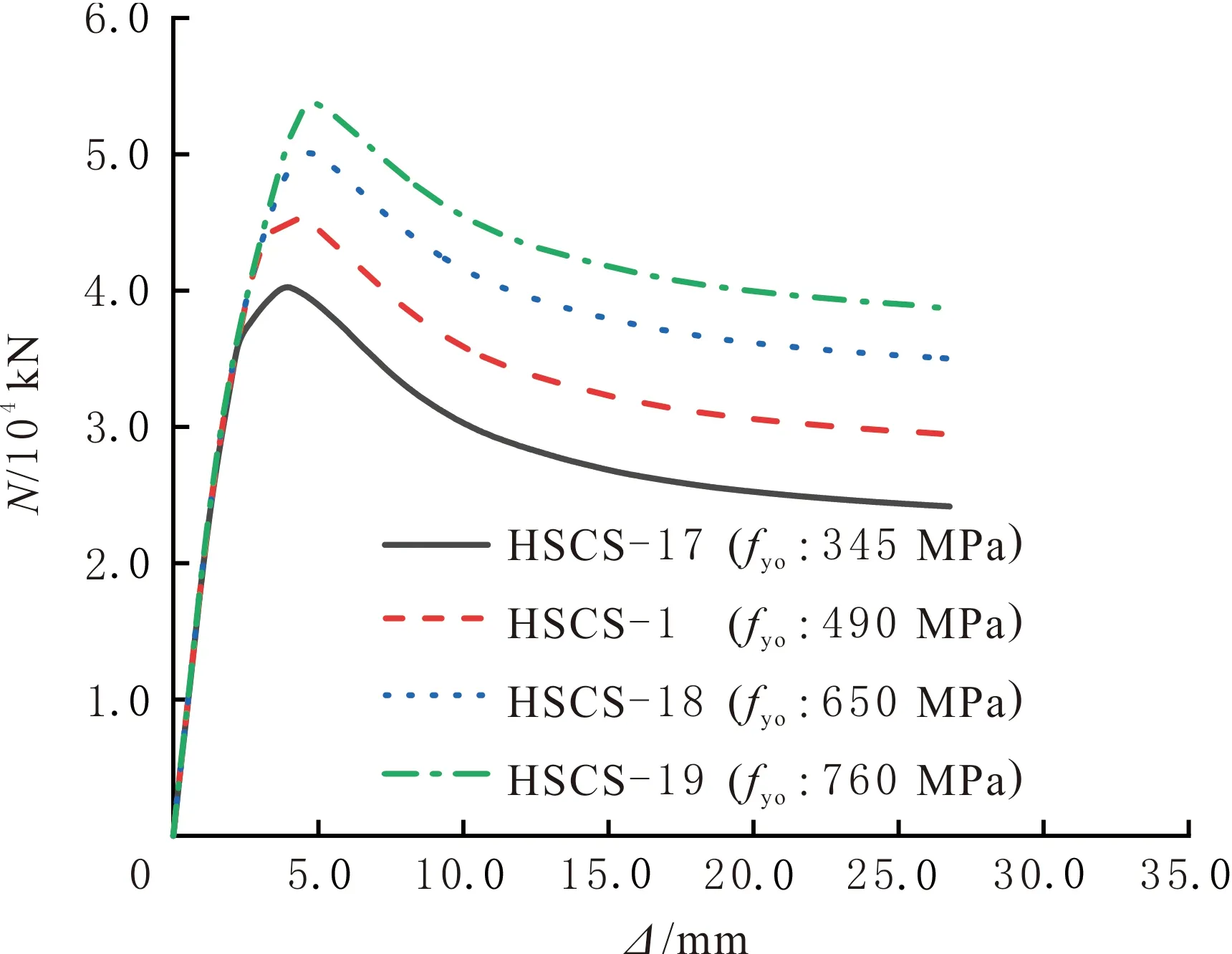
图12 不同fyo的HSCS组合短柱试件N—Δ曲线

图13 不同fck的HSCS组合短柱试件N—Δ曲线
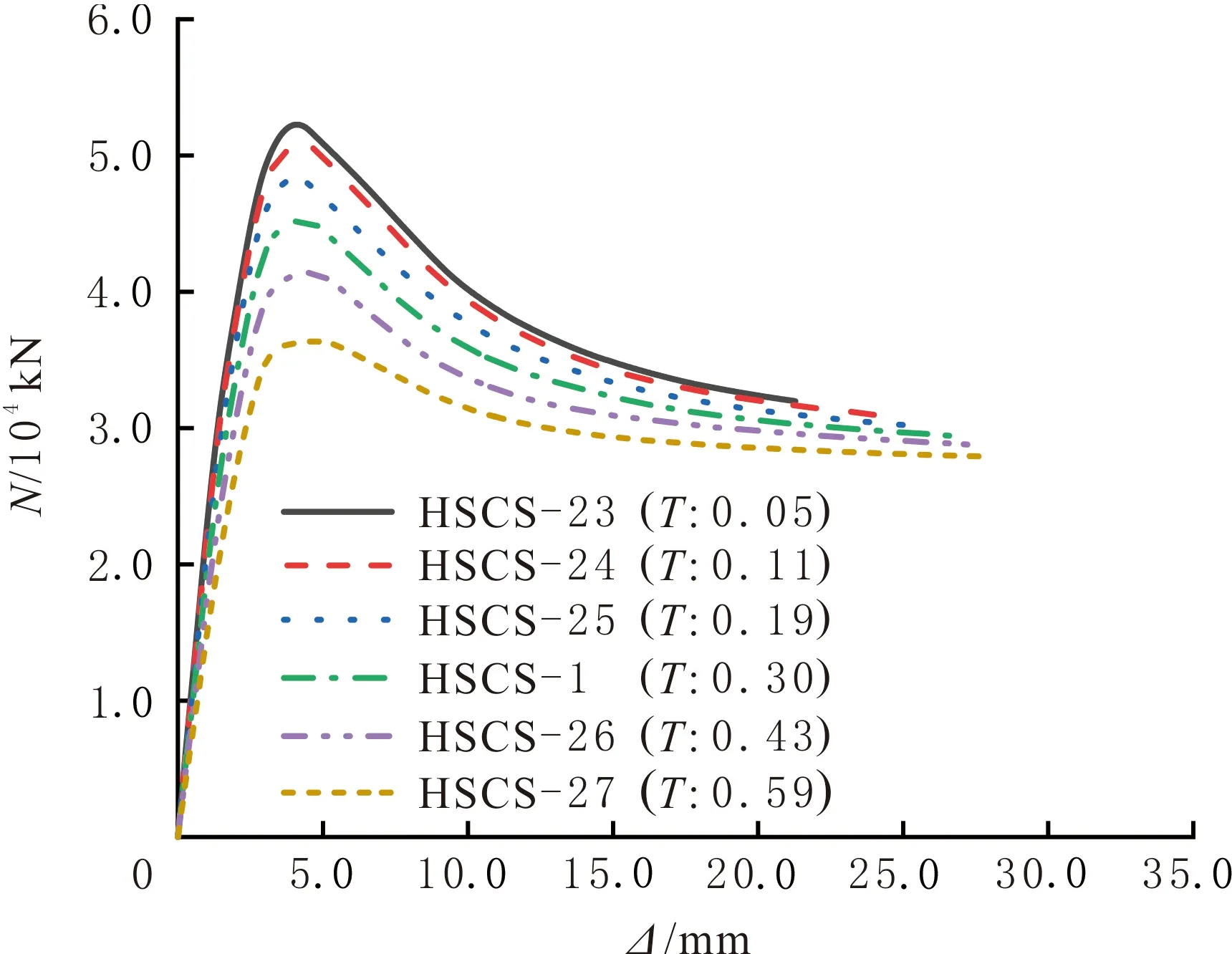
图14 不同T的HSCS组合短柱试件N—Δ曲线
3.2 组合柱轴压承载力计算式
根据单层钢管混凝土的受力机理,韩林海[16]建立精度较高的单层钢管混凝土柱的轴压承载力计算公式。该公式简单实用,具有较高的预测精度,表达式为
Nu1=(1+1.8ξ)fckAc,
(3)
式中:Ac为混凝土的截面面积;Nu1为单层钢管混凝土柱轴压承载力。
采用式(3)对HSCS组合短柱试件的轴压承载力进行计算,计算结果见图15和表3。
由图15可知,采用式(3)并不能准确计算文中HSCS组合短柱试件的轴压承载力,极限承载力的预测误差大于±15%,全部试件的轴压承载力被低估,不满足计算要求。根据叠加法的基本思想,结合式(3)、HSCS组合短柱试件的构造形式及其参数影响规律,进行试件轴压承载力的简化计算。
HSCS组合短柱的轴压承载力主要由3部分组成,分别为外高强方钢管、环混凝土和内圆钢管。
Nu2=Acfcc+Asifyi+Asofyo,
(4)
式中:Nu2为HSCS组合短柱轴压承载力;fcc为考虑约束效应下环混凝土的轴压承载力;Asi和Aso分别为内圆钢管和外高强方钢管的截面面积。
根据HSCS组合短柱的构造特点,轴压承载力为
Nu3=(1-T)Nu2,
(5)
式中:Nu3为HSCS组合短柱的轴压承载力。
式(3)对单钢管混凝土柱具有较高的预测精度,假设Nu2=Nu1,即HSCS组合短柱在未考虑中空构造的前提下,与单钢管约束混凝土组合柱等价,考虑高强钢材的轴压承载力增益为
Nu3=(1-T)(1+1.8ξ)fckAc+Asifyi+Asofyo。
(6)
采用式(6)对27根HSCS组合短柱轴压承载力进行计算,计算结果见图16和表3。
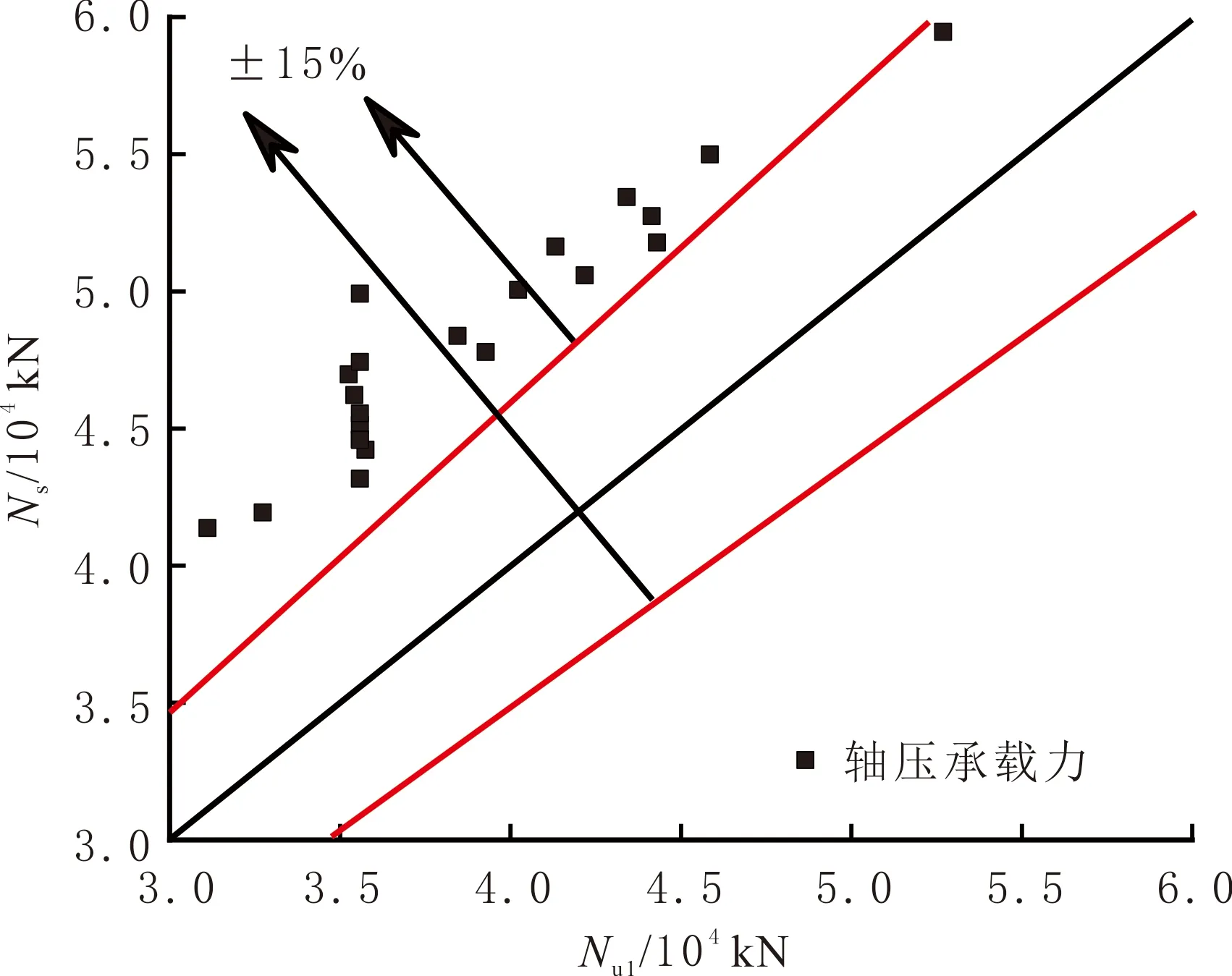
图15 Nu1与Ns的离散程度对比
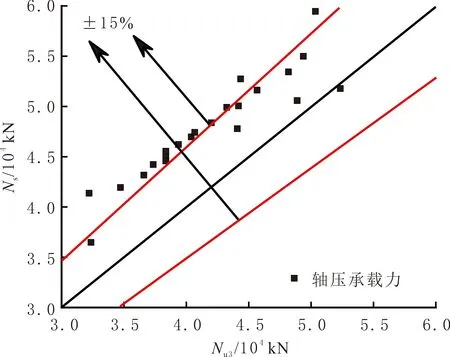
图16 Nu3与Ns的离散程度对比
由图16可知,采用式(6)虽然对HSCS组合短柱轴压性能的预测精度改变较大,但部分试件的计算结果不满足小于15%的要求,原因是低估高强钢材对组合柱的约束效应。基于1stOpt软件,对式(6)进行精度拟合:
Nu= (1-T)(1+2.79ξ)fckAc+Asifyi+Asofyo,
(7)
式中:Nu为精度拟合后的轴压承载力,其计算结果见图17和表3。
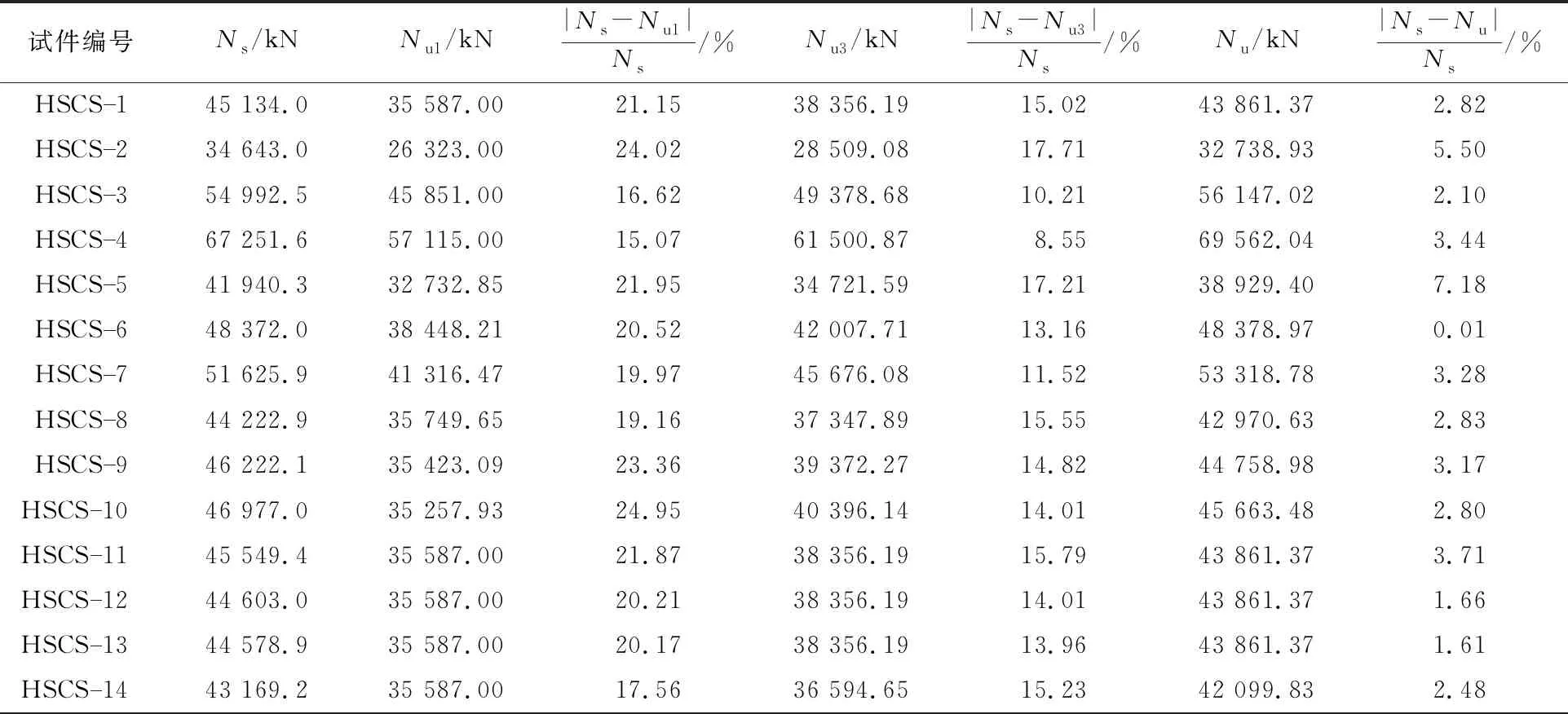
表3 HSCS组合短柱试件轴压承载力对比
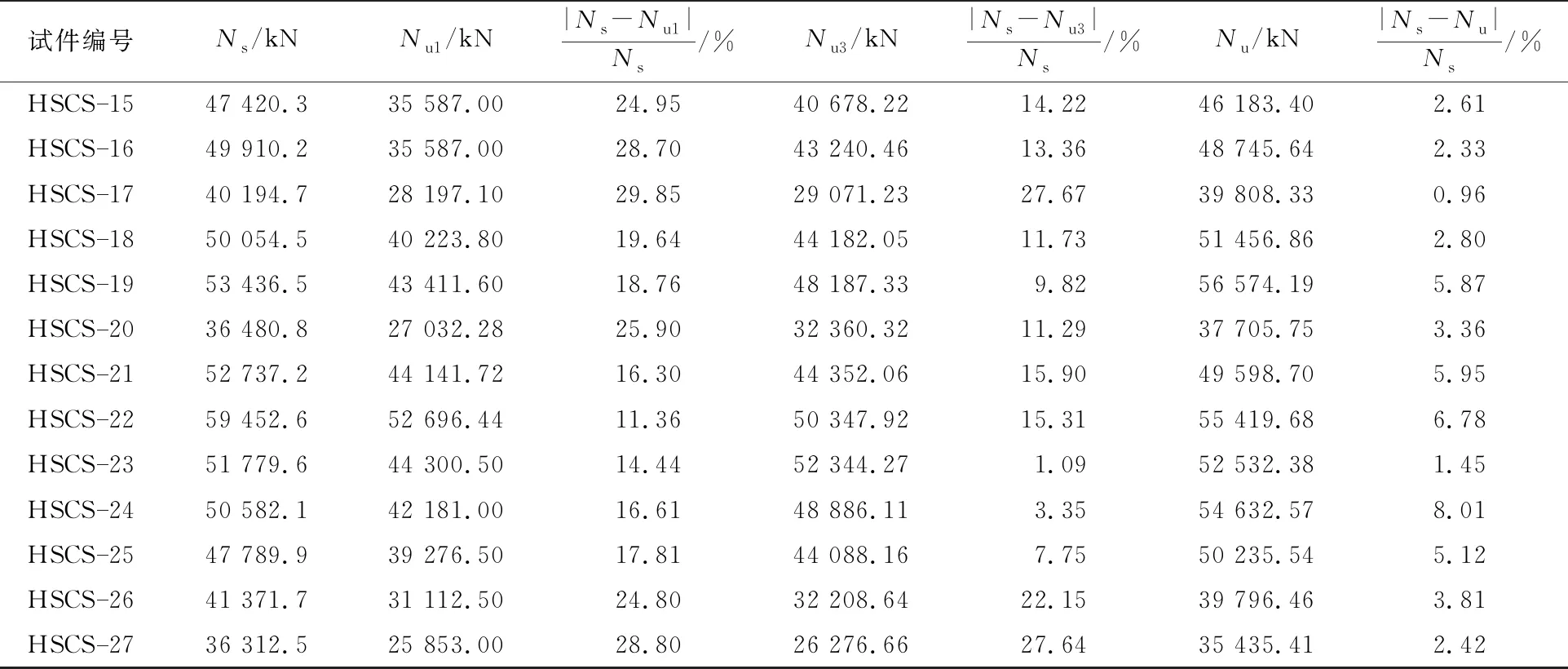
续表3
Ns与Nu离散程度对比见图17。由图17可知,二者之间吻合良好,最大误差为8.01%,具有较高的预测精度,可满足工程需要。

图17 Nu与Ns的离散程度对比
4 结论
(1)采用ABAQUS有限元分析软件对6根类似试验试件开展数值仿真分析,获得轴向荷载—应变关系曲线,与相关试验曲线吻合程度较高,轴压承载力的最大误差为7.07%。
(2)随B、to、fyi、fyo和fck的增加,HSCS组合短柱的轴压承载力显著提高;随T的增加,轴压承载力逐渐减小。随T的增加,HSCS组合短柱的极限位移显著提高;随试件B、to、fyi和fyo增加,HSCS组合短柱极限位移逐渐减小。
(3)为实现较好的轴压性能,建议T的最佳取值范围为0.1~0.3。
(4)基于叠加原理、HSCS组合短柱的构造形式和单钢管混凝土柱轴压承载力的计算表达式,建立适用于HSCS组合短柱轴压承载力的计算表达式,最大误差为8.01%,具有较高的预测精度,可满足工程需要。

