近地小行星动能撞击的最优撞击方案分析

李涛,覃金贵,任磊生,李毅

(中国空气动力研究与发展中心超高速空气动力研究所,绵阳 621000)

1 引言

太阳系中除了八大行星等大质量天体外,在火星和木星轨道之间还分布着大量小行星。其中,轨道接近地球的小行星统称为近地小行星,其轨道半长轴小于1.3个天文单位 (AU)。根据小天体中心网站 (https://www.minorplanetcenter.net)的数据,目前已经发现了27504颗近地小行星,其中,有2203颗小行星和地球的最小轨道交会距离小于0.05AU,平均直径大于140m,被称为潜在威胁小行星 (PHA)。它们有可能会与地球发生危险交会,甚至撞击地球,造成巨大破坏。1908年,一颗直径50m的小行星在俄罗斯西伯利亚通古斯上空爆炸解体,损毁了超过2000km2的原始森林[1]。2013年,一颗直径约20m的小行星在俄罗斯车里雅宾斯克上空解体爆炸,造成约1500人受伤,3000栋房屋受损[2]。当撞击地球的小行星尺寸较大时,则会造成灾难性后果[3]。随着人类对近地小行星危害的认识逐渐深入,关于行星防御问题的研究也日益得到重视,相继有核爆偏离、引力拖船、动能撞击等多种行星防御方案被提出来,其中,直接动能撞击是目前而言技术成熟度最高、最有可能实现的防御方案[4]。

动能撞击是指利用撞击器对小行星进行超高速撞击,使其获得速度增量并偏离原来的轨道,从而避免与地球轨道交会。在动能撞击防御方案中,涉及撞击器从地球发射到实施撞击的轨道设计、任务实施过程中的深空通信、撞击过程的动量传递以及撞击后效的观测评估等各方面问题的研究。由于将一定质量的航天器送入太空、并通过轨道机动等使其最终能以一定速度撞击目标小行星,成本极为高昂,且撞击器能够达到的质量和相对撞击速度受当前发射能力和空间推进技术的限制。因此,对撞击器轨道进行优化设计一直是防御方案的研究重点。近年来,已有不少文献开展了相关研究工作,如Izzo等[5]提出小行星受动能撞击后轨道偏转距离的解析计算公式,并将其应用到撞击器行星际轨道转移方案的优化设计中;Yuki等[6]提出先撞击 “中间”小行星、再利用 “中间”小行星撞击目标小行星的动能撞击方案,并对撞击器的轨道转移方案进行优化设计;王艺睿等[7]考虑运载约束,对动能撞击Apophis小行星的撞击器轨道转移方案进行分析优化。总体而言,这些工作多是在考虑发射能力、发射窗口、预警时间等多约束条件下,对动能撞击轨道方案的整体优化设计。

有别于前述研究,本文只考虑撞击器对小行星进行动能撞击及随后的轨道偏转过程,以偏转Apophis小行星为例,提出一种对小行星最优撞击位置和撞击方位的初步设计方法。首先,根据小行星和地球的轨道交会几何关系,确定动能撞击Apophis的轨道偏转目标;随后,将Apophis受动能撞击及随后的轨道偏转简化为脉冲推力变轨,利用二体轨道理论,获得对Apophis的最优撞击轨道位置和最优撞击方位;最后,建立考虑主要摄动力的Apophis数值轨道预报模型,对按最优撞击方位进行动能撞击的轨道偏转效果进行量化评估,验证所提优化方法的可行性。

2 动能撞击Apophis的轨道偏转目标

Apophis为阿登型近地小行星,它和地球均在以太阳为焦点的椭圆轨道上运动。由于两天体的绕日轨道不共面,Apophis在过两轨道面交线时距地球最近,撞击地球风险也最大。理想情况下,动能撞击Apophis应该使其面内变轨,且考虑小行星正对地心撞击的最恶劣撞击场景,变轨后Apophis过近地点的位置应该比撞击前至少偏离1个地球半径,才能完全消除撞地威胁。这意味着,动能撞击Apophis的轨道偏转目标就是要使其撞击后通过轨道面交线上的一个确定的位置点(预定偏转点),如图1所示。实际上,由于大部分近地小行星的绕日轨道都与地球轨道异面,因此这一结论也适用于它们。

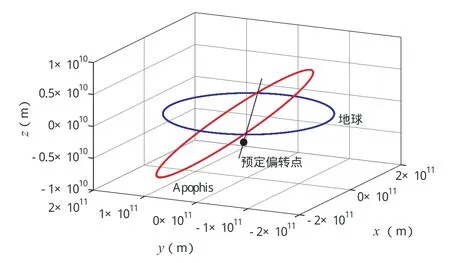
图1 J2000日心黄道系下Apophis与地球轨道Fig.1 The orbits of Earth and Apophis(Heliocentric ecliptic J2000)

在二体轨道假设下,根据Apophis和地球的轨道参数,可以计算得到Apophis过与地球轨道面交线位置时的两个真近点角为53.4°和233.4°。其中,f=233.4°时,Apophis与地球相距最近,为8.7486×10-4AU,取地球赤道半径为RE=6378.137km,即可确定预定偏转点的位置矢量。

表1 Apophis和地球轨道根数 (J2000日心黄道系)Table 1 The orbit elements of Earth and Apophis(Heliocentric ecliptic J2000)

3 动能撞击Apophis的撞击方位优化

动能撞击Apophis的实质是使其瞬间获得一个速度增量,从而使其轨道按预定目标偏转。在初步分析中,这一过程可以等效为对Apophis进行轨道面内的脉冲推力变轨。寻找最优撞击方位,等效为寻找满足预定变轨目标的最小脉冲速度增量,需要确定的量包括该速度增量的大小、方向以及施加时Apophis的轨道位置。

该问题如图2所示,记动能撞击时Apophis日心轨道的真近点角为f1,对应位置矢量r1,速度矢量u1,动能撞击给Apophis的脉冲速度增量记为Δv。动能撞击后,Apophis将经过预定偏转点r2,对应的原日心轨道真近点角为f2=233.4°。由二体轨道边值理论可知,通过两固定点的轨道有无数条,问题的关键是确定脉冲速度增量最小(燃耗最优)的变轨方案。

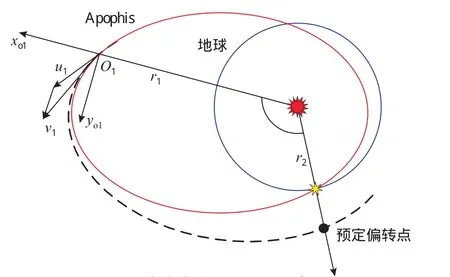
图2 动能撞击Apophis示意图Fig.2 Diagramfor kinetic impact of Apophis

照此方法,可以求出在Apophis不同轨道位置 (以变轨点和预定偏转点的轨道相位差Δf表示)进行动能撞击时需要提供的最小撞击速度增量,如图3所示。图中,Δf=0o对应Apophis距地球最近时的轨道位置,总体而言,撞击点越靠近该位置,为使Apophis到达预定偏转点,所需的脉冲速度增量将越大。并且,脉冲速度增量的值并不是关于Δf=0o轴对称的。动能撞击点与预定偏转点的相位差在0°～180°区间时,脉冲速度增量随Δf增大而单调递减。但相位差在-180°～0°时,脉冲速度增量并不完全随Δf增大而单调递增,而是在Δf=-164.2°处存在一个极小值,对应的速度增量为0.3267m/s,该点即为对Apophis动能撞击的最优位置点,对应Apophis的日心轨道真近点角为68.8°。

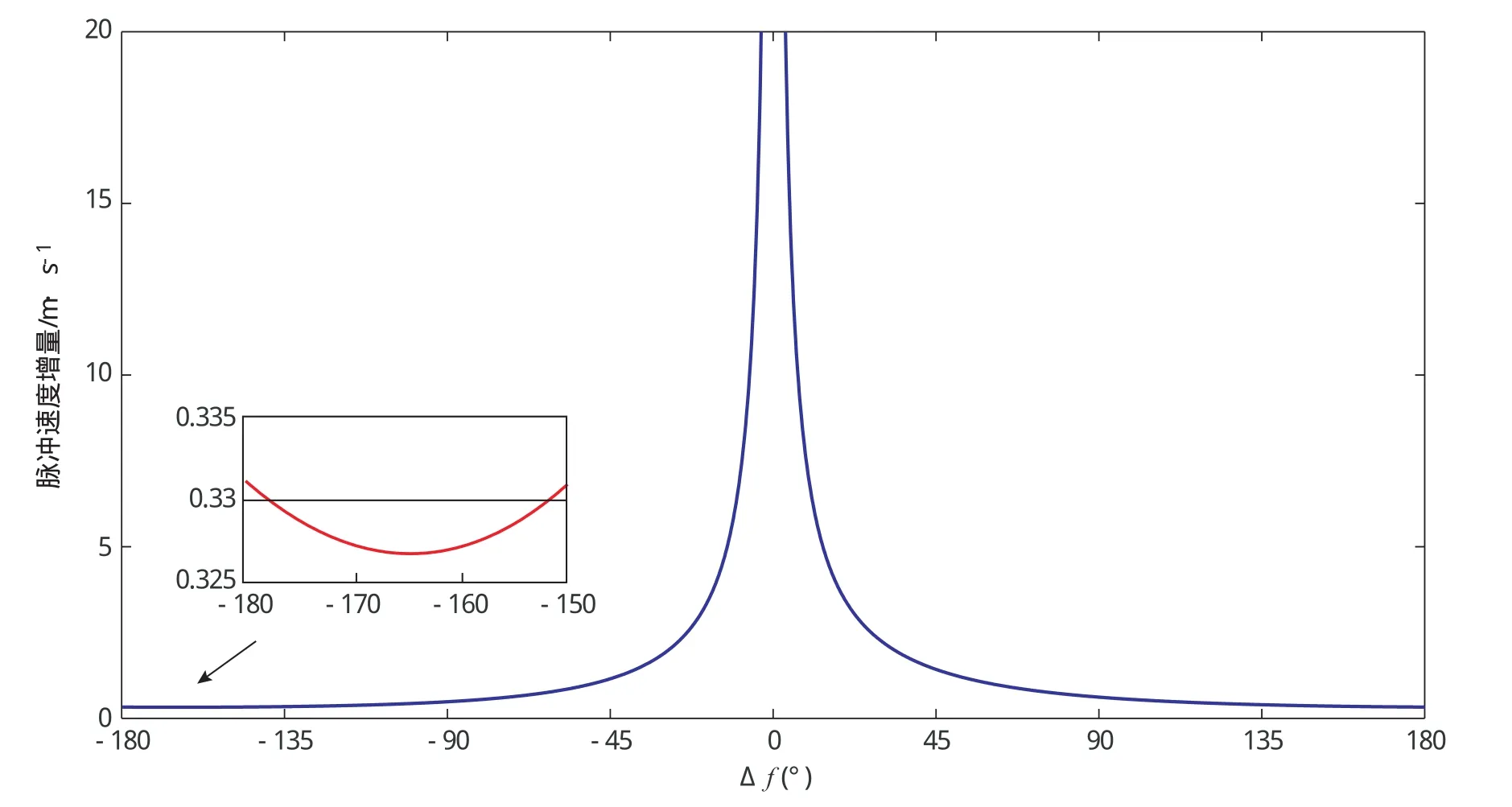
图3 在Apophis不同轨道位置进行动能撞击需要的最小速度增量Fig.3 The minimum velocity increments corresponding to different impact locations

图4给出了在Apophis不同轨道位置进行动能撞击时,对应的最优撞击方位角。这里,该方位角定义为在给定撞击点进行动能撞击时,满足要求的最小脉冲速度增量与Apophis轨道速度的逆时针夹角。

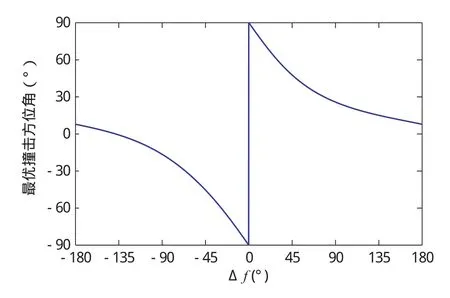
图4 在Apophis不同轨道位置进行动能撞击的最优撞击方位角Fig.4 The optimal impact azimuths corresponding to different impact locations

由图4可知,在Apophis不同轨道位置进行动能撞击时,对应的最优撞击方位角通常不为0,意味着最优脉冲速度矢量与Apophis的轨道速度方向并不重合。在Δf=-164.2°处 (最优撞击位置)对Apophis进行动能撞击时,撞击方向与Apophis轨道速度矢量的逆时针夹角为5.2°是最优的,对应的脉冲速度增量即为0.3267m/s。

需要指出的是,这一速度增量是在将轨道偏转距离设定为RE=6378.137km这一保守值的前提下得到的。实际情况中,往往不需要如此大的偏转距离。按前述优化方法对不同偏转距离下的最优撞击点、撞击方位及速度增量的计算结果表明,最优撞击点位置和撞击方位是固定的,而所需的速度增量则会随偏转距离减小而线性减小。进一步考虑动能撞击Apophis的动量传递效率,分析该脉冲速度增量的工程可实现性。基于经验公式[10]的初步分析表明,假设撞击器质量能达到5t,由于撞击器大致沿Apophis轨道运动方向进行撞击,则相对撞击不可能太大,假设撞击速度能达到6km/s,玄武岩材质小行星的速度增量能达到约0.5cm/s,对应的轨道偏转距离约为100km。如果考虑小行星内部具有23%的孔隙率,则6km/s撞击速度所能提供的速度增量约为0.1cm/s,对应约20km的轨道偏转距离。

4 动能撞击Apophis的轨道偏转效果评估

近地小行星的轨道运动除了受中心天体太阳的引力作用外,还受太阳系中其他大质量天体的第三体引力、太阳光压、后牛顿效应等摄动力影响[11]。本节建立Apophis的受摄轨道预报模型,利用数值轨道外推对Apophis受动能撞击后的实际轨道偏转量进行评估,从而验证上述优化方案的可信度。预报模型中,摄动力主要考虑太阳系8大行星、月球、冥王星系统和三个大质量小行星Ceres、Pallas、Vesta对Apophis的第三体引力,轨道外推则采用带步长控制的7(8)阶Runge-Kutta-Fehlberg算法[12]实现。

假设撞击器在前述最优撞击位置按最优撞击方位角对Apophis进行动能撞击,针对Apophis获得的不同速度增量,利用轨道预报模型计算撞击前后,小行星过地球轨道面的时间偏差和轨道偏转量,结果如图5和图6所示。

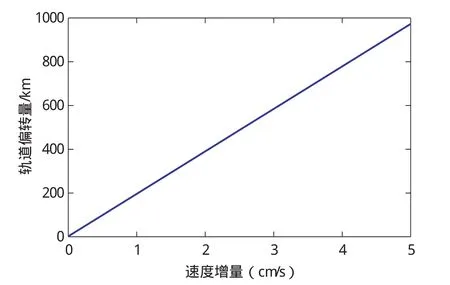
图6 不同速度增量对应的Apophis轨道偏转量Fig.6 Orbit deflection distances of Apophis corresponding to different velocity increments

图5横轴为Apophis受动能撞击后获得的速度增量,纵轴为撞击前后Apophis过地球轨道面的时间差;图6纵轴则表示撞击前后,Apophis过地球轨道面的轨道偏转量。由图可知,Apophis获得的速度增量与其过地球轨道面的时间差和轨道偏转量大致成正比。按最优撞击方案进行动能撞击时,每给Apophis提供1cm/s的速度增量,将使其过地球轨道面的时间推迟约16.5s,并使其在过地球轨道面时向外偏转约200km。据此外推至速度增量为0.3267m/s的情况,则轨道偏转量约为6534km,与第2节预设的轨道偏转量RE=6378.137km基本吻合,这充分说明利用二体轨道理论进行最优撞击方位的初步分析,得到的结果是可信的。

5 结论

本文以动能撞击Apophis小行星为例,将小行星受撞击及随后的轨道偏转过程简化为脉冲推力变轨,给出了一种基于二体轨道假设的最优撞击方案设计方法。该方法得到的计算结果表明,在Apophis日心轨道真近点角为68.8°时,撞击器沿与轨道速度逆时针夹角为5.224°方向进行动能撞击是燃耗最优的。利用考虑主要摄动力的Apophis数值轨道预报模型进行验证表明,在前述最优撞击方案下,每给Apophis提供1cm/s的速度增量,可使其获得约200km的实际轨道偏转量,与预设的轨道偏转目标基本吻合,证明该方法除了计算简单快速外,还具备一定精度,可为更精细的撞击防御方案设计提供参考。