空中多目标威胁程度判别及打击方案

白洁静

摘  要：该文利用层次分析法，对空袭中20个具有不同属性的空袭目标，进行了属性与威胁程度之间关系的评价，并按照威胁程度由高到低对来袭目标进行了排序;为了保护己方战略要地以及80 km外的物资要地，根据给定的25个战略防空武器的相关数据及打击要求，建立了优化模型，针对来袭目标设计最佳打击方案，使得来袭目标对我方的威胁程度降到最低。

关键词：层次分析法  一致性检验  优化模型  目标函数  约束条件

中图分类号：E919                             文献标识码：A                    文章编号：1672-3791（2021）01（a）-0001-06

Judging the Threat Degree of Multi-targets in the Air and Strike Plan

BAI  Jiejing*

（Nanjing Vocational College of Information Technology  Department of Quality-oriented Education， Nanjing， Jiangsu Province， 210023 China）

Abstract：In this paper， the analytic hierarchy process（AHP）is used to evaluate the relationship between the attributes and threat level of 20 air raid targets with different attributes， and the incoming targets are ranked according to the threat level from high to low. In order to protect our strategic locations and material locations 80 kilometers away， an optimization model was established to design the best strike plan for the incoming targets so as to minimize the threat of the incoming targets to us according to the relevant data and strike requirements of 25 strategic air defense weapons.

Key Words：Analytic hierarchy process（AHP）; Consistency check; Optimization model; Object function; Constraint condition

1  問题的提出

该题目来源于2018年第二届全国大学生军事数学建模竞赛C题，红方探测到20批蓝方空袭目标的属性信息，为保证红方在反空袭综合演练中取得胜利，为保证红方在反空袭综合演练中取得胜利，要求建立数学模型解决以下问题：问题一：对来袭目标的属性与威胁程度之间的关系进行评价;问题二：建立判别来袭目标威胁程度的数学模型，并按照威胁程度由高到低对来袭目标进行排序;问题三：如果在红方战略要地A点正北方80 km处有一个物资要地B点，在空袭中需要红方重点保护，A点装备的战略防空武器的相关数据已给定，已知20批蓝方空袭目标的航向在一定时间内始终为正西方，请根据来袭目标对A、B点的威胁程度，设计一种最佳打击方案，并对该方案的实施效果进行评价。

2  模型的建立及求解

2.1 针对问题一：建立层次分析模型判断目标属性的威胁程度及来袭目标的威胁程度

首先，建立层次分析模型[1]。如图1所示，目标层为来袭目标威胁度，准则层是目标属性，分别为目标类型、目标距离、目标速度、目标高度、目标干扰能力、目标到达时间，方案层则为蓝方来袭的1～20号目标。

然后，构造方案层对准则层各属性的判断矩阵。为了使各属性之间的比较能够有效量化，我们引入确定判断矩阵中元素aij值的9级标度。对于来袭目标类型我们判定类型越大威胁度越高，即威胁度：大>小>直升机;对于方位角[2]，我们判定方位角越接近π/2威胁度越高;目标与阵地A之间距离越大，阵地A点相对越安全，即威胁度越小;目标速度越大，威胁度越大;目标高度越高，威胁度越小;来袭目标干扰能力越高，威胁度越大。利用以上的6个评估准则和表1的标度值定义，可以将20个目标针对6个属性分别确定出判断矩阵，即做出6个20×20的判断矩阵。通过计算判断矩阵的最大特征值对应的特征向量，然后将特征向量进行归一化之后作为目标属性的权重向量。

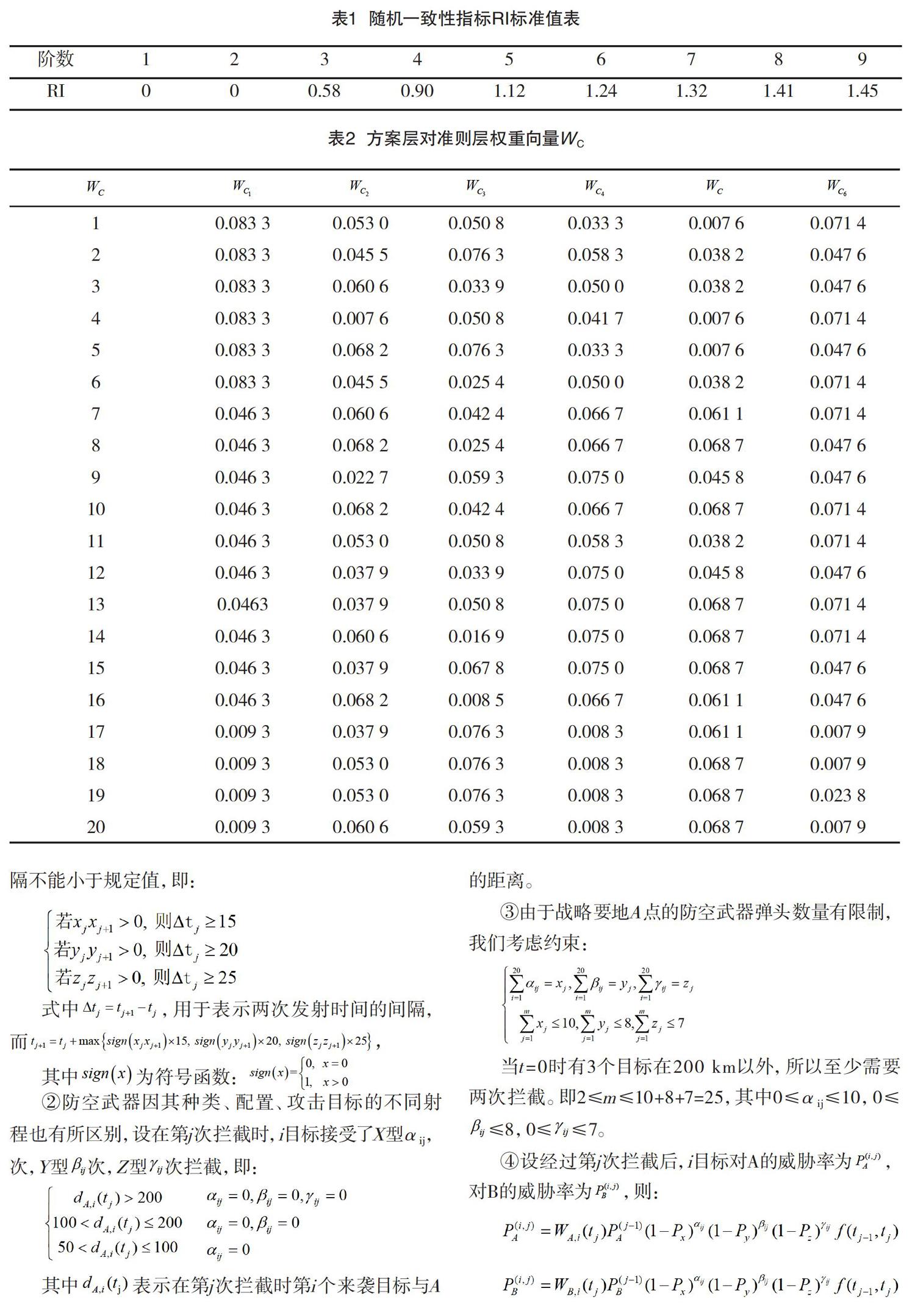
在确定最终权重之前我们先对判断矩阵进行一致性检验[3]，计算判断矩阵一致性指标，一致性比率，其中RI为n阶比较矩阵的平均一致性指标，也称随机一致性指标，具体值见表1。

当CR<0.1时，我们认为判断矩阵具有一致性，其归一化之后的特征向量可以作为目标属性的权重向量（该模型6个方案层对准则层的矩阵都通过一致性检验）。

将方案层对准则层各个属性进行归一化处理，整理得到20×6的整体权重矩阵WC。

最后列出准则层6个属性对于目标层的判断矩阵（见表3）。

通过MATLAB程序运算[5]可以得出最大特征值=6.070 6，权重向量：

[0.242 7，0.038 3，0.110 2，0.133 4，0.184 1，0.291 2]T

经验证该模型中的一致性指标CI=0.014 12，一致性比率CR=0.011 39<0.1，由此，表3所列矩阵通过一致性检验。由该判断矩阵计算得到的权重向量中元素值越大，说明其对应的属性威胁度越大。因此我们得到结论：来袭目标的干扰能力对于威胁程度影响最大，其次是来袭目标类型，而来袭目标的高度、速度、距离影响相对小一点，目标方位角对威胁程度的影响最小。

2.2 针对问题二：计算方案层对目标层的权重向量

我们已经得到20个来袭目标相对准则层6个属性的权重向量所组成的矩阵WC及来袭目标属性的权重W，将W作为该模型准则层对目标层的权重WP，综合两层判断矩阵得到方案层对目标层的权重向量。

根据向量中元素值越大，说明其对应的目标威胁度越大，方案层20个来袭目标的威胁程度排序结果为：13>10>6>7>2>14>15>1>11>4>3>8>5>9>16>12>19>18>20>17。

2.3 针对问题三：建立优化模型设计最佳打击方案

（1）模型的建立。

为了建立优化模型[4]，我们做以下假设：设第j次拦截时发射了X型防空武器xj枚，Y型防空武器yj枚，Z型防空武器zj枚。发射时间为tj，j=1，2，3，…，m。其中m为总的拦截次数。

①因为防空武器有发射时间间隔的要求，所以对于3种型号的防空武器，发射第j枚和第j+1枚的时间间隔不能小于规定值，即：

式中，用于表示两次发射时间的间隔，而，

其中为符号函数：

②防空武器因其种类、配置、攻击目标的不同射程也有所区别，设在第j次拦截时，i目标接受了X型αij，次，Y型次，Z型次攔截，即：

其中表示在第j次拦截时第i个来袭目标与A的距离。

③由于战略要地A点的防空武器弹头数量有限制，我们考虑约束：

当t=0时有3个目标在200 km以外，所以至少需要两次拦截。即2≤m≤10+8+7=25，其中0≤αij≤10，0≤      ≤8，0≤≤7。

④设经过第j次拦截后，i目标对A的威胁率为，对B的威胁率为，则：

此处为与t相关的威胁函数，随时间越长，受威胁程度越大。经过j次拦截之后，A及B所受到的威胁率分别为：

所以第j次拦截后，我方所受的总威胁率为：

最终目标函数表达式：

至此模型建立完成，即求解带约束的优化模型    如下：

约束条件：

（2）模型的求解。

在2.2中我们已经求得来袭目标对于A点的威胁程度，因为物资要地B点也需要重点保护，我们针对B点也计算了威胁程度。由于B点在A点正北方80 km处，目标方位角和目标距离都需要重新计算，在得到来袭目标相对于B点目标距离与目标方位角数据后，应用与问题2.2同样的求解方式，得到蓝方来袭目标对B点的威胁程度的权重向量WB：

即20个来袭目标对于物资要地B点的威胁度排   序为：

13>6>14>10>7>4>2>3>9>15>1>11>8>12>16>5>19>18>20>17

模型计算中由于所有目标在几分钟内进入拦截射程，而拦截导弹最多在485 s内（25×7=175，20×8=160，15×10=150）打完，所以我们忽略该段时间内我方的装备损失，在计算中认为，受时间影响不大，即为WA和WB。对于权重λ，注意到若A被击毁，则B也就不受保护，考虑到侧重保护B，所以对于A点的保护权重取λ=0.6。而f（t）由于时间较短，我们认为不受时间影响，即f（t）=1。

所以模型的目标函数可以简化为：

通过MATLAB编程求解，求得的拦截方案即拦截步骤为：

第一步：在时间t=0时，即在起始时间为0时用Y、Y、Z、Y、Z、Y、Z、Y、Z、Y、Z、Y、Z、Y、Z型武器分别拦截目标13、6、2、4、3、11、9、12、5、19、18、17、10、7、15。

第二步：在时间t=45.058 7时，用一枚X型武器拦截目标15。

第三步：在时间t=104.172 3和t=115.172 6时，用两枚X型武器分别拦截目标10和7。

第四步：在时间t=150.610 8时，用两枚X型武器拦截目标1;在时间t=155.493 8时，一枚X型武器拦截目标8;在时间t=158.965 9时，用两枚X型武器拦截目标14。

第五步：在时间t=221.086 3时，用一枚X型武器拦截目标16。

第六步：在时间t=469.076 6时，用一枚X型武器拦截目标20。

这六步的间隔时间足以让同类型的导弹发射。

结论：按以上拦截，经过469.076 6s后，我方拦截武器发射完毕，经过895.235 0s后，我方受危险程度由原来的1降为0.181 8，危险降低了1-0.181 8=0.818 1，即毁伤目标的概率达到了0.818 1。

3  模型的评价

从所给防空武器的类型来看，X型武器的毁伤目标概率为0.6，Y型武器的毁伤目标概率为0.85，Z型武器的毁伤目标概率为0.8，即相当于两枚X型武器重复打击目标的毁伤概率为1-（1-0.6）2=0.84，和一枚Y型武器的毁伤概率是基本类似的。这样以来，我们可以认为给定的防空武器的打击力度和5+8=13枚Y型，7枚Z型的毁伤概率相似。这样相当于20枚毁伤概率为0.8和0.85的防空武器打击20个攻击目标，其最大的毁伤概率只能达到0.85。从以上我们的模型计算结果可以看出，威胁率从1下降到0.181 8，毁伤概率为0.818 1，已经是不错的打击方案。

4  结语

该文利用层次分析法和最优化方法解决了空襲问题中对空袭目标威胁程度的判断，并设计了最优打击方案。从中我们可以看出数学方法对于解决很多实际生活中问题是大有益处的，因此，以数学建模为契机，基于数学建模竞赛的模型为案例设计数学教学，可以激发学生学习数学的兴趣，鼓励学生学以致用，从而对于数学教学也有极大的帮助。

参考文献

[1] 王鹏.基于系统动力学的网购快递配送及时率的模型分析与研究[J].科技资讯，2020，18（16）：10-11.

[2] 昌飞，张欣毅，林莹.防空作战多目标威胁度排序决策研究[J].兵器装备工程学报，2016，37（2）：159-161，168.

[3] 王古超，陆俊峰，袁翔，等.基于AHP的全向移动机器人综合评价[J].科技创新导报，2018，15（36）：109-110.

[4] 邵丽云，王艳雪.数学建模论文写作课教学案例——以《关于外卖垃圾问题的分析与解决》一文为例[J].中学数学教学参考，2019（16）：11-14.

[5] 薛辉，刘铁林，乔治军，等.基于回合制的火力分配优化问题建模方法研究[J].兵工学报，2018，39（8）：1655-1664.

[6] 李子龙.基于科学竞赛驱动的案例式程序设计教学模式研究[J].科技资讯，2020，18（15）：126，128.